修正的EKPF算法在固定单站被动目标跟踪中的应用*



修正的EKPF算法在固定单站被动目标跟踪中的应用*

申正义a,闫抒升a, 王晓军a, 王晴晴b

(空军预警学院 a.预警模拟训练中心； b.图书馆,湖北 武汉430019)

摘要：基于以角度、角度变化率、多普勒频率变化率信息为观测量的固定单站被动目标跟踪系统，引入扩展卡尔曼粒子滤波(EKPF)算法对定位结果进行滤波处理。理论分析和仿真实验证明了其滤波性能在该系统中的优越性。针对EKPF算法运算量大、实时性差的问题，通过对部分粒子进行间隔EKF采样，将EKPF算法进行修正。修正的EKPF算法既有效降低了运算量，又增加了粒子的多样性，使粒子集更加逼近真实的后验概率密度函数。计算机仿真表明，与传统的EKPF算法相比，修正算法在保证滤波性能基本不变的前提下，算法实时性得到了有效提高。

关键词：粒子滤波；扩展卡尔曼滤波；固定单站被动目标跟踪；间隔采样

0引言

被动目标定位跟踪系统本身并不向外辐射电磁波，具有受环境影响小、隐蔽性强和作用距离远等优点。仅利用单个固定观测站接收目标辐射源辐射的信号来估计目标位置和运动状态的过程称为固定单站被动目标定位与跟踪。固定单站被动目标定位与跟踪系统只需一个被动目标信号接收站，具有更强的隐蔽性，且设备简单、系统相对独立，作为目标探测的新手段，可与有源雷达相结合，提高系统的互补性和抗毁性[1-3]。利用角度、角度变化率、频率和多普勒频率变化率信息实现固定单站被动目标定位，是一种快速高精度的定位方法。但参数测量都带有误差，为实现快速高精度的固定单站被动目标定位，除了要有高精度的参数测量技术外，还需要研究高性能的跟踪滤波算法，以便最大限度地利用观测量提供的目标运动信息，同时也可减轻对参数测量技术的压力。

固定单站被动目标跟踪是典型的非线性滤波过程，经典的滤波算法是扩展卡尔曼滤波(extended Kalman filter，EKF)，但当系统非线性较强时，EKF算法存在的线性化误差大、对初始状态的依赖性大、协方差矩阵易出现病态等问题将更加突出，会导致滤波结果不稳定[4]。针对强非线性非高斯系统，Gordon等人于1993年提出了粒子滤波(particle filter，PF)算法。标准PF算法选择先验概率密度作为重要密度函数，没有充分考虑当前时刻的观测值，存在粒子退化现象[5]。为此，文献[6]从改进重要密度函数的选择入手提出了扩展卡尔曼粒子滤波算法(extended Kalman particle filter，EKPF)。针对实际系统往往是非高斯非线性的情况，本文将文献[6]所描述的EKPF算法应用于固定单站被动目标跟踪中，并与EKF算法进行比较，在初始误差或测量误差较大时滤波精度优于EKF算法，但EKPF算法的本质是在重要性采样阶段用EKF算法对每个粒子进行更新，这无疑加大了算法的运算量，使算法的实时性变差。为此本文提出一种修正的EKPF算法，通过对部分粒子间隔进行EKF采样，在保证滤波性能基本不变的前提下有效提高了算法的实时性。

1固定单站被动目标定位跟踪原理

1.1被动目标定位方法

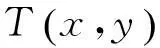
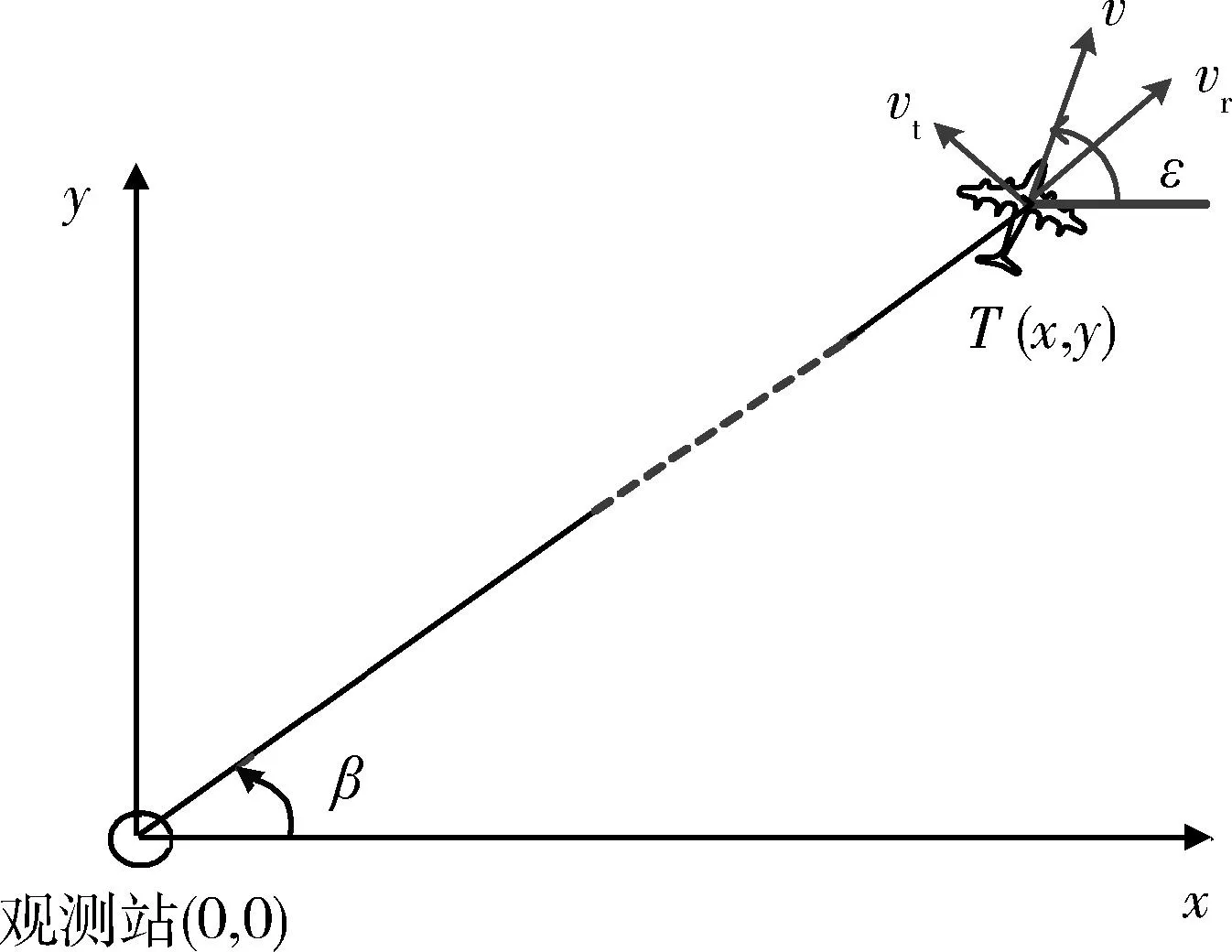
图1　二维平面固定单站被动目标定位几何示意图Fig.1　Geometry diagram of 2D plane fixed single　　　 observer passive target localization

1.2被动目标跟踪状态方程

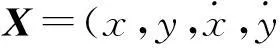
Xk=Φk,k-1Xk-1+υk-1，

(1)

式中：υk-1为状态噪声；Φk,k-1为状态转移矩阵：

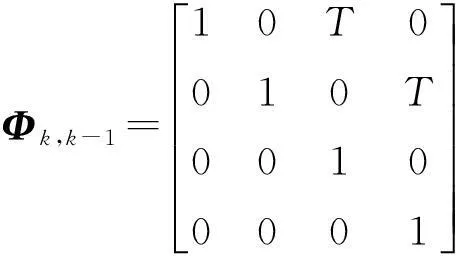
(2)

式中：T为观测间隔时间。

1.3被动目标跟踪观测方程

根据固定单站被动目标定位方法，得出目标状态向量与观测量之间的关系，建立系统的观测方程如下：

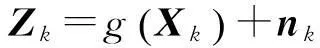
(3)

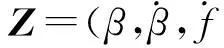
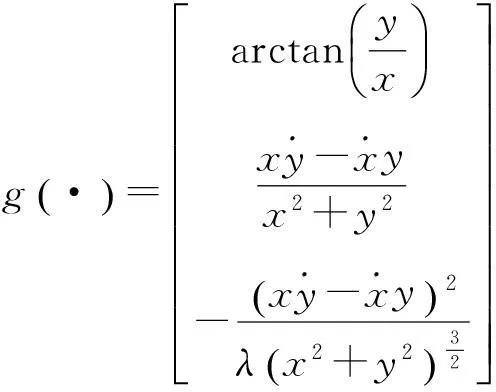
(4)

式中：λ为来波信号波长。

根据系统状态方程和观测方程，利用一定的滤波算法对目标状态进行递推估计，就可得到目标的位置与速度信息，从而实现固定单站对空中运动目标的被动跟踪。

2EKPF及其修正算法

2.1EKPF算法

粒子滤波是一种基于蒙特卡罗方法的近似贝叶斯滤波算法，其核心思想是用大量离散的随机采样点(粒子)及其相应权值来近似系统变量的后验概率密度函数，以样本均值代替积分运算，从而获得状态变量的最小方差估计，这些粒子根据贝叶斯准则进行适当的加权和递归传播。粒子数目越多，这种蒙特卡罗近似就越接近于状态变量的真实后验概率分布[8]。实际上直接从后验分布采样是很困难的，通常引入一个容易获取样本的重要密度函数，标准PF算法选择先验概率密度函数作为重要密度函数，由于没有考虑当前的观测值，重要性权值的方差会随时间而随机递增，使得粒子的权重集中到少数粒子上，即所谓粒子退化问题。减轻粒子退化的常用方法是使用重采样技术[9-10]。

减轻粒子退化现象的另一种方法是选择合适的重要密度函数。EKPF算法从修正重要密度函数的选择入手，利用EKF算法对每个粒子进行更新，将最后得到的近似后验密度作为重要密度函数，引入了当前时刻的最新观测值，在一定程度上避免了粒子退化现象，提高了粒子滤波算法的估计精度[11]。

EKPF算法的具体运算流程如下：

(1) 初始化粒子

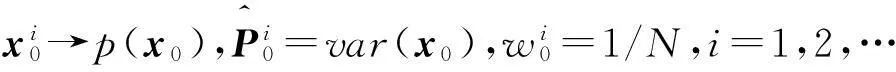
(2) 更新粒子

(3) 计算重要性权值

按式(5)计算粒子的重要性权值，并进行归一化。

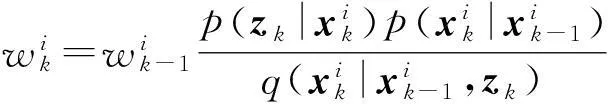
(5)

(4) 重采样

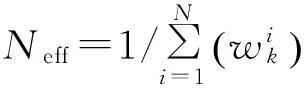
(5) 状态估计

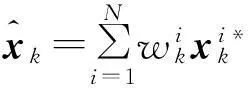
(6)

2.2修正的EKPF算法

EKPF算法的本质是在重要性采样阶段用EKF算法对每个粒子进行更新，这无疑加大了算法的运算量，使算法的实时性变差。为此，本文对EKPF算法作如下修正：

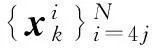
经过这样修正的算法，既考虑了当前时刻的观测值、先验概率对后验概率分布的影响，又增加了粒子的多样性，同时有效降低了计算量，提高了算法的实时性。

修正的EKPF算法的运算步骤如下：

(1) 初始化粒子

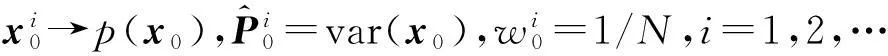
(7)

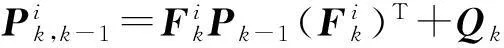
(8)

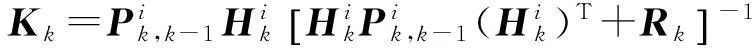
(9)

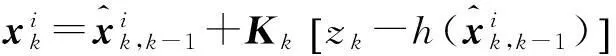
(10)

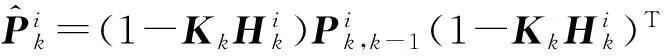
(11)

(3) 重要性采样

(4) 重要性权值计算

按式(5)计算粒子的重要性权值，并进行归一化。

(5) 重采样

(6) 状态估计

按照式(6)求出状态估计值。

3滤波算法性能仿真对比

3.1仿真条件

在二维平面，假设观测站位于坐标原点，目标的初始位置为(80，180)km，按照(-250，80)m/s的速度做匀速直线运动，辐射源信号波长λ=33 mm，观测间隔时间T=1 s，观测时间150 s。为比较各种滤波算法的定位跟踪效果，采用相对位置误差(RPE)来评价各算法的滤波性能[12]。RPE的定义为

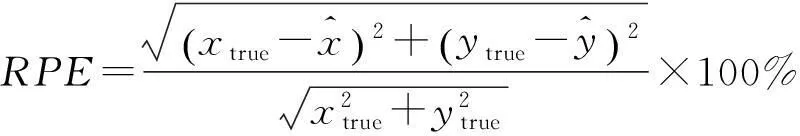
(12)

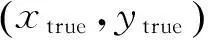
本文在以下2种条件下，分别进行100次蒙特卡罗实验，考察修正的EKPF算法相对于传统的EKF和EKPF算法的滤波性能。在EKPF及其修正算法中，均取粒子数N=200，重采样门限Nth=66。RPE<5%时认为算法收敛一次。

3.2仿真结果分析

经计算机仿真，得到在条件1和条件2下，100次蒙特卡罗实验中3种算法的收敛次数和单次滤波所需的时间，如表1所示。

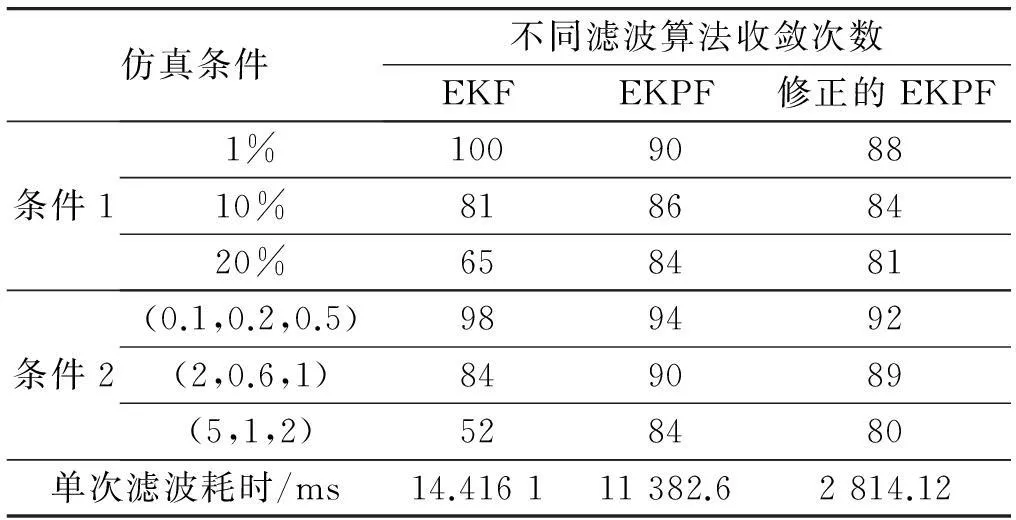
表1　100次实验中各算法收敛次数及滤波耗时对比

从表中可以看出，在初始误差较小时，EKF算法的收敛次数高于EKPF和修正的EKPF算法，说明粒子滤波算法在小初始误差情况下的优势并不明显；随着初始误差的增大，EKF算法的收敛次数明显下降，而EKPF和修正的EKPF算法的收敛次数下降不明显。因此，2种粒子滤波算法性能受初始误差影响较小，相对于EKF算法稳定性更好。在测量误差较大时，EKPF算法和修正的EKPF算法的收敛次数均大于EKF算法，说明测量误差较大时粒子滤波算法在固定单站被动目标跟踪系统中的性能优于EKF算法。从单次滤波所需的时间来看，EKPF算法明显高于EKF算法，实时性较差，修正的EKPF算法相对于原EKPF算法滤波耗时明显下降。

为了提供3种算法更直观的滤波性能比较，图2和图3分别给出了3种算法在不同初始误差和不同测量误差条件下RPE的统计平均曲线。

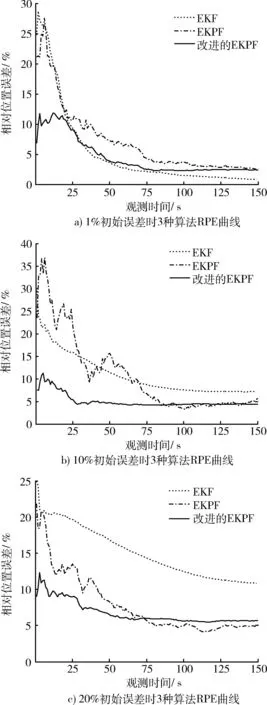
图2　不同初始误差时3种算法性能比较Fig.2　Performance comparison of 3 algorithms　　　with different initial errors

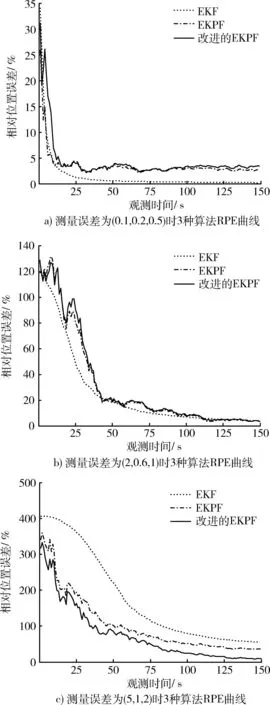
图3　不同测量误差时3种算法RPE曲线Fig.3　Performance comparison of 3 algorithms　　　withdifferent observation errors

通过上述仿真实验，结合理论分析可知，3种算法中，在小初始误差和小测量误差时，EKF算法的性能最优。随着初始误差和测量误差的增大，EKPF及其修正算法表现出更优的滤波性能。可见，EKPF及其修正算法在系统初始误差和测量误差较大时，表现出更大的优势。从仿真中还可看出，EKPF算法相对于EKF算法对初始值的依赖性较小，这是由于EKPF算法将EKF算法与对非线性估计较好的粒子滤波算法相融合，采用EKF算法来更新粒子，滤波过程结合了当前时刻的观测信息，使粒子集更加逼近真实的后验概率密度函数。尽管EKPF算法的滤波性能更稳定，但其运算量也远大于EKF算法，这是因为EKPF算法需对每个粒子进行EKF滤波预测，其运算量约为EKF算法的N倍再加上重采样和滤波结果输出所需的运算量。也就是说EKPF算法滤波性能的提高是以牺牲运算时间为代价的。而修正的EKPF算法只有N/4的粒子进行了EKF采样更新，既增加了粒子的多样性，使粒子分布更加合理，减轻了粒子退化现象，又有效降低了算法的运算量。仿真结果也表明，修正的EKPF算法在保证原EKPF算法滤波性能基本不变的前提下，有效降低了运算量，提高了算法的实时性。

需要注意的是，从仿真结果看，修正的EKPF算法尽管运算量大幅下降，但其滤波耗时仍非常高，这是由于计算机模拟仿真时N个粒子的运算是顺序处理的。实际工程应用中，在硬件上实现粒子滤波时N个粒子的运算是并行处理的，且随着高速计算机的出现，运算速度大幅提高，因此修正的EKPF算法具有很大的工程应用潜力。

4结束语

本文在介绍以角度、角度变化率、多普勒频率变化率为观测量的固定单站被动目标定位与跟踪原理的基础上，引入扩展卡尔曼粒子滤波算法对定位结果进行滤波处理，并针对EKPF算法运算量大、实时性差的问题，对其进行了改进，提出了修正的EKPF算法。理论分析和仿真结果表明，粒子滤波算法对非线性系统具有较好的估计能力，但由于EKPF算法需对每个粒子进行EKF滤波预测更新，运算量大幅增加。修正的EKPF算法只对N/4的粒子进行EKF采样，其余3N/4的粒子仍采用先验概率分布进行重要性采样，这样既降低了算法的运算量，又增加了粒子的多样性，使粒子集更加逼近真实的后验概率密度函数，在保证滤波性能基本不变的前提下，有效提高了算法的实时性，具有较好的应用潜力。

参考文献：

[1]孙仲康，郭福成，冯道旺，等．单站无源定位跟踪技术[M]．北京：国防工业出版社，2008．

SUN Zhong-kan，GUO Fu-cheng，FENG Dao-wang． Passive Location and Tracking Technology by Single Observer[M]．Beijing：National Defense Industry Press，2008．

[2]熊群力，陈润生，杨小牛，等． 综合电子战[M].2版．北京：国防工业出版社，2008．

XIONG Qun-li，CHEN Run-sheng，YANG Xiao-niu，et al．Integrated Electronic Warfare [M].2nd ed．Beijing：National Defense Industry Press，2008．

[3]何明浩．雷达对抗信息处理[M]．北京：清华大学出版社，2010．

HE Ming-hao．Radar Information Processing [M]．Beijing：Tsinghua University Press，2010．

[4]郁春来．利用空频域信息的单站被动目标定位与跟踪关键技术研究[D]．长沙：国防科学技术大学电子科学与工程学院，2008．

YU Chun-lai．Research on Crucial Technologies for Single Observer Passive Location and Tracking via Spatial-Frequency Domain Information [D]．Changsha：National Defense Science and Technology University of Electronic Science and Engineering College，2008．

[5]Olivier Cappe，Simon J Godsill，Eric Moulines．An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo[J]．Proceedings of the IEEE．2007，95(5)：899-924．

[6]FREITAS J F G，NIRANJAN M，GEE A H.Sequential Monte Carlo Methods to Train Neural Network Models[J]．Neural Computation，2000，12(4)：995-993．

[7]徐璟，何明浩，郁春来，等．固定单站被动目标跟踪算法性能分析[J]．电子信息对抗技术，2011，26(1)：29-33．

XU Jing，HE Ming-hao，YU Chun-lai，et al．Analysis of Fixed Single Observer Passive Target Tracking Algorithm Performance [J]．Electronic Information Warfare Technology，2011，26(1) ：29-33．

[8]梁军．粒子滤波算法及其应用研究[D]．哈尔滨：哈尔滨工业大学，2009．

LIANG Jun．Research on Particle Filter Algorithm and Its Application[D]．Harbin：Harbin Institute of Technology，2009．

[9]李孟敏．改进粒子滤波算法及其在目标跟踪中应用研究[D]．合肥：合肥工业大学，2011．

LI Meng-min．Research of an Improved Particle Filter Algorithm and Its Application in Target Tracking[D]．Hefei：Hefei University of Technology，2011．

[10]刘金华．基于粒子滤波单站无源定位跟踪技术研究[D]．成都：电子科技大学，2008．

LIU Jin-Hua．Research on Tracking Technology of Single Observer Passive Location Based on Particle Filter[D]．Chendu：University of Electronic Science and Technology of China，2008．

[11]万洋，王首勇．非线性滤波算法的性能分析[J]．空军雷达学院学报，2010，24(2)：111-114．

WAN Yang，WANG Shou-yong．Analysis of Performances on Nonlinear Filtering Algorithms [J]．Joumal of Air Force Radar Academy，2010，24(2)：111-114．

[12]郁亮．单站无源定位跟踪技术研究[D]．成都：电子科技大学，2006．

YU Liang．Research on Technology of Single Observer Passive Location and Tracking [D]．Chendu：University of Electronic Science and Technology of China，2006．

Application of Modified EKPF Algorithm in Target Tracking Technology ofFixed Single Observer Passive Localization

SHEN Zheng-yia，YAN Shu-shenga，WANG Xiao-juna，WANG Qing-qingb

(AFEWA，a．Center of Early Warning Training & Simulation；b．Library，Hubei Wuhan 430019，China)

Abstract:By taking the fixed single observer passive location and tracking system with angle, angle rate-of-change and Doppler frequency rate-of-change information as the concept of measurement,and the location result is processed by the extended Kalmanparticle filter algorithm. The theoretical analysis and simulation results show thesuperiority of the filter performance in the location system. Aimingat the problem of large computation burden and poor real-time, the EKPF algorithm is modified by interval sampling to part of the particle with EKF algorithm. The modified EKPF algorithm can effectively reduce the computation burden, increase the diversity of particles, and makethe particles closer to the true posterior probability density function. Simulation result shows that compared with the traditional EKPF algorithm, the proposed algorithm ensures the performance of the filter and the real-time of algorithm is effectively improved.

Key words:particle filter (PF)；extended Kalman filter (EKF)；passive target tracking by fixed single observer；interval sampling

中图分类号：TN957.51

文献标志码：A

文章编号：1009-086X(2015)-02-0116-06

doi:10.3969/j.issn.1009-086x.2015.02.019

通信地址：430019湖北省武汉市黄浦大街288号模拟训练中心E-mail：xinyu430010@163.com

作者简介：申正义(1982-)，男，山西五台人。讲师，硕士，主要研究方向为雷达信号处理。

* 收稿日期：2014-03-06；
修回日期：2014-06-27