基于蚁群算法的广义扩展双桥问题的最优解*



基于蚁群算法的广义扩展双桥问题的最优解*

孙婷1，孙晔1，向新1，许蕴山1，张远贵2

(1.空军工程大学,陕西 西安710038； 2.中国人民解放军95810部队气象台,北京100076)

摘要：在扩展双桥实验的基础上，提出了同时考虑路径长度和多项边成本的广义扩展双桥问题，该模型是多准则决策问题的基础模型。提出了一种基于蚁群算法的多准则寻优方法，该方法采用了边成本矩阵和相应的目标函数描述问题，并将信息素与其相关联。仿真结果证明，通过合理的参数设置，蚁群算法能有效得出广义扩展双桥问题的最优解。同时，退化为扩展双桥问题时，该算法同样适用。该实验有效证明了蚁群算法对于多准则决策问题的解决具有很好的指导意义。

关键词：多准则决策；扩展双桥实验；蚁群算法

0引言

双桥实验是研究蚂蚁通过信息素浓度选择路径行为的经典实验。Marco Dorigo等人在简单双桥模型的基础上，提出了一种扩展双桥模型[1]。扩展双桥模型的特点在于，图的上部是一条不带环路但并非最短的路径，图的下部是一系列路径的集合，包括2条最短路径，也包括有限数目的更长的不带环路的路径，以及无穷多的更长的带环路的路径。扩展双桥问题是蚁群算法的经典实验，由于其路径选择可能性增大，而且存在环路问题，该问题的求解对于深刻揭示蚁群算法具有重要意义。常规讲，扩展双桥实验就是以路径长度最短为准则的决策问题。

但是在实际工作中，可能很难遇见根据单一准则进行决策的情况[2-3]。一般都会从对最优解产生影响的各个方面进行全面的考虑和分析，最终得出全局的最优方案，这类问题就称为多准则决策问题[4-5]。针对这样的问题，也有一些研究从其他方面进行考虑，比如Satish Talreja提出了一种新的观念，针对多准则决策问题，采用了层次分析法进行决策，并利用简单双桥问题为背景进行了说明[6]，但是方法具有明显局限性。遗传算法[7-8]、粒子群算法[9]等算法也已被运用于该类问题。蚁群算法已被证明能出色地应用于各类组合优化问题[10-11]，是一种并行的高效的元启发式算法。本文中，以扩展双桥问题为基础，讨论出现边成本的情况下如何求解扩展双桥问题。为了明确起见，在本文中具有边成本的扩展双桥问题称为广义扩展双桥问题。该模型即为多准则决策问题的基础模型，并使用蚁群算法求解，最终证明蚁群算法对于求解多准则决策问题的有效性。

1广义扩展双桥模型

广义扩展双桥模型如图1所示。即在扩展双桥问题中同时考虑路径长度和多个路径成本，由寻最短路径转化为寻兼顾全局的最优路径。假设每条边都有n类不同的路径成本(图中标注了第k类成本)，蚂蚁经过不同的边所花费的代价不同。选择次短路径成本小但距离较长，而选最短路径距离短但成本大，如果基于成本考虑则最短距离的选择不是最优的。在本文中，针对最优策略讨论广义的扩展双桥问题的解，而原本的扩展双桥问题是最优策略为最短距离的特殊情况。

图1　第k类成本时带边成本的扩展双桥的图示Fig.1　Generalized extended double bridge with cost k

为了讨论方便起见，这里设定目标函数为路径距离和路径成本的函数，

F=f(Length,Cost1,…，Costi,…，Costn)，

(1)

式中：Length为路径长度；Costi为其他n项路径成本。对于最简单的情况，目标函数可以选取为路径长度和成本的线性和，ak为加权值，则

(2)

关于路径成本的建模，考虑到蚂蚁是逐点移动的，成本是在逐点移动过程中产生的，为此，本文提出边成本矩阵C来描述广义扩展双桥问题的各边成本，针对边成本Costk，有边成本矩阵如下：

(3)

式中：k表示成本标示，在本文模型中由于选用n类边成本，应该采用n个边成本矩阵，且

(4)

采用蚁群算法求解，首先对蚂蚁行为进行界定。

(1) 蚂蚁从源节点起逐点决策前往目的节点，此过程称为前向模式，在此过程中，为了防止蚂蚁直接返回，前一点排除在下一个拟前往点之外。第k只蚂蚁由节点i到节点j的概率为

(5)

式中：Ni为当前节点i的邻点的集合(不包含该节点的上一点)；τij为节点i和节点j连接边上累积的信息素值；α为信息素指数。

在前向过程中，蚂蚁将按式(1)计算并记录经过路径和相应路径成本。

(2) 蚂蚁到达目的节点后按原路径返回，此过程称为反向模式，在此过程中，蚂蚁将在每边释放信息素：

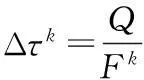
(6)

式中：Q为信息素强度；Fk为第k只蚂蚁所走路径的目标函数值。

则每边信息素为原有信息素加上一次迭代过程中该边蚂蚁释放的信息素之和，如下：

τij←τij+∑Δτk.

(7)

考虑到信息素的挥发因素，式(7)可以修正为

τij←(1-ρ)τij+∑Δτk，

(8)

式中：ρ为信息素蒸发系数，蒸发系数的取值关系到算法的收敛行为[12]。

(3) 蚂蚁回到原点的时刻不同，先到的蚂蚁不受其他蚂蚁影响，继续开始寻找新的路径。在本文中，每边的路径长度相同，并默认单位时间完成一个边的移动，该单位时间就是算法迭代的一个周期。

蚁群算法的流程图如图2所示。

2仿真实验

在仿真试验中，为简单起见本文仅考虑只有一种边成本的简单模型。如图3所示，各点的边上标注的为路径成本。

由图3得到的边成本矩阵：

图2　蚁群算法流程图Fig.2　Flow chart of ACO

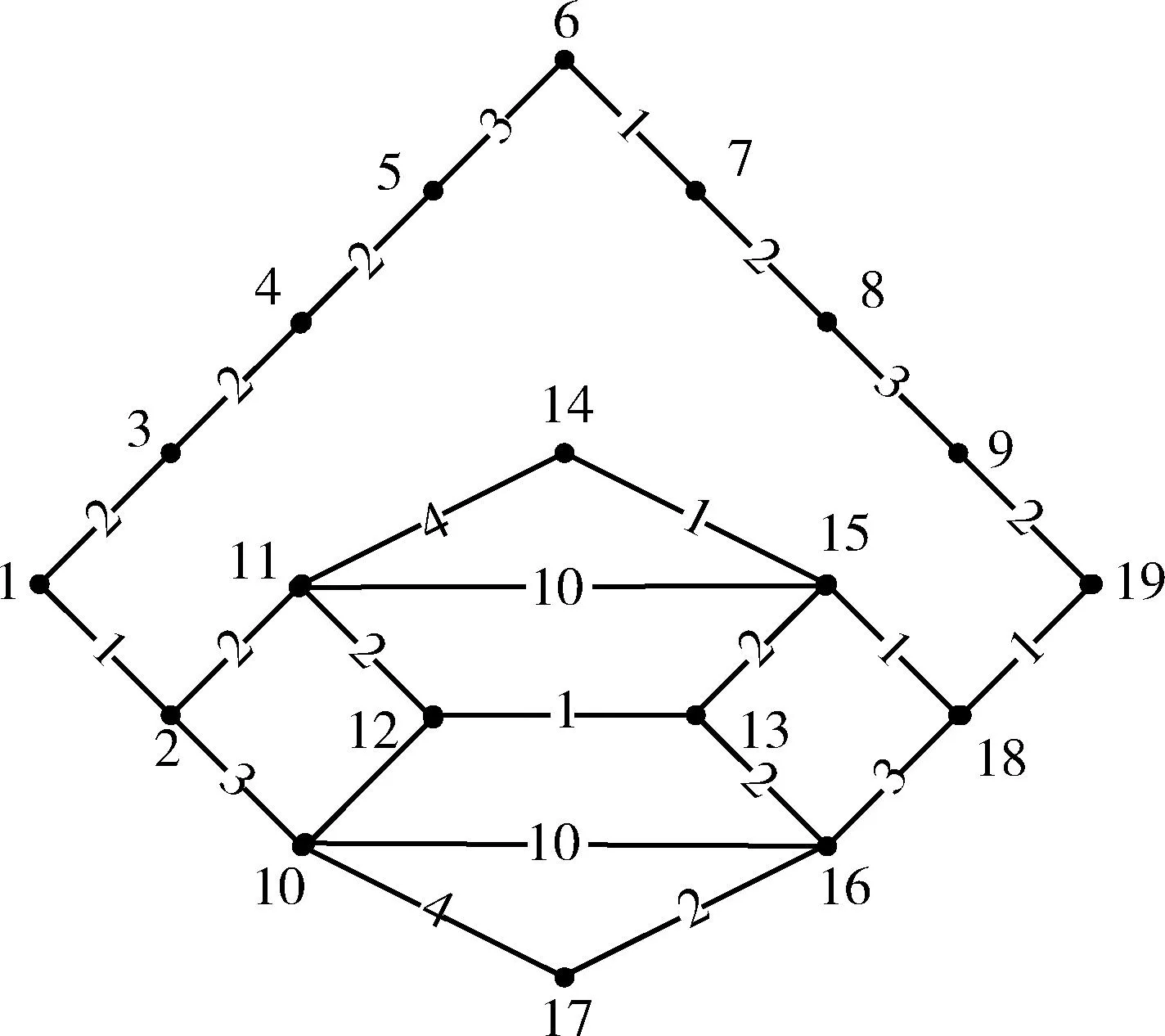
图3　只有一种边成本的广义扩展双桥实验的图示Fig.3　Generalized extended double bridge　　　with one kind of edge cost

此时的目标函数简化为

F=a0·Length+a1·Cost.

(9)

设定a0=1，a1=0.5，取参数α=1，信息素强度Q=1，蚂蚁只数m=128，同时设定迭代次数为5 000次。在该问题的求解过程中，考虑了不同信息素蒸发系数(ρ∈{0,0.01,0.1})对实验结果的影响，结果如图4所示。

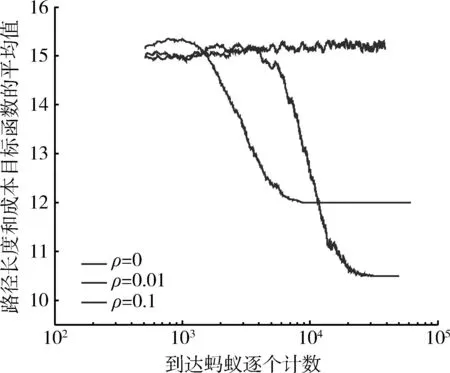
图4　考虑边成本时蚂蚁路径生成结果Fig.4　Ant path considering edge cost

图4中，路径长度和成本目标函数的平均值是指使用蚂蚁最近找到的4m条路径求得的目标函数值计算得出的。由图4可得，ρ=0时，即不存在信息素的蒸发时，结果不收敛，目标函数平均值在15附近浮动，蚂蚁无法寻找到最优路径。当信息素蒸发存在(ρ=0.01和ρ=0.1)时，最后结果都达到了收敛。但当蒸发系数过大(ρ=0.1)时，信息素蒸发过快，无法给以后的蚂蚁起很好的引导作用，最后都收敛到了次优路径中。当蒸发系数为一适当的取值(ρ=0.01)时，在信息素的正反馈作用下，蚂蚁都收敛到了最优路径。此时的最优路径为：1-2-11-14-15-18-19。实验证明，通过合理地设置参数，蚁群算法能有效地解决广义扩展双桥问题。

在特殊情况下，不考虑边成本时，广义扩展双桥问题就退化成了扩展双桥问题。模型图与图3相似，但边上成本均为0，矩阵C为零矩阵。此时的目标函数为

F=Length=n-1，

(10)

式中：n为蚂蚁经过的点数，问题退化为经典的求最短路径问题。在这种情况下同样设置了不同的蒸发系数ρ∈{0,0.01,0.1}，观察了蚂蚁找到的路径的生成情况，结果如图5所示。由图可知，不存在信息素的蒸发(ρ=0)时，结果不收敛，平均移动值在7.5附近浮动。当信息素蒸发存在(ρ=0.01和ρ=0.1)时，最后结果都达到了收敛。但ρ=0.1时，结果收敛到了长度为6的次短路径；ρ=0.01时，所有蚂蚁都寻找到了长度为5的最短路径，即1-2-10-16-18-19。实验结果与Marco Dorigo给出的结果相符，表明扩展双桥问题确为广义双桥问题的特例。

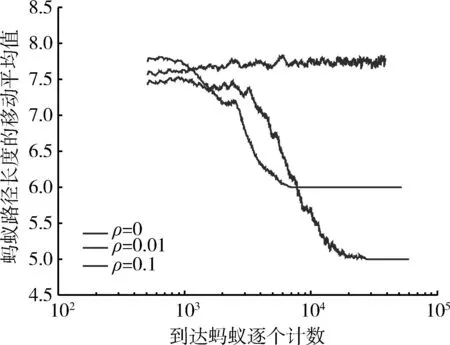
图5　不考虑边成本时蚂蚁路径生成结果Fig.5　Ant path without edge cost

3结束语

由单准则决策问题扩展成多准则决策问题，广义扩展双桥模型比扩展双桥模型具有更强的实用性。本文提出了边成本矩阵来描述边成本并给出了求解的目标函数,并使用蚁群算法求得了广义扩展双桥问题的最优解。仿真结果证明，通过不同蒸发系数的设置，证明了蚁群算法对于广义扩展双桥问题求解的有效性。当不考虑边成本时，广义扩展双桥就退化为扩展双桥问题。仿真实验得出了与理论相一致的结果。实验结果表明，蚁群算法能有效应用于多准则决策问题，对于其他应用也有很好的指导意义。

参考文献：

[1]DORIGO M ,STUTZLE T. Ant Colony Optimization[M].London: The MIT Press, 2004: 15-20.

[2]张洪波, 汤国建. 弹道导弹防御中多目标拦截的策略[J]. 现代防御技术, 2007, 35(2): 23-26.

ZHANG Hong-bo, TANG Guo-jian. The Tacises of Multitarget Interception in Ballistic Missile Defense[J]. Modern Defense Technology, 2007, 35(2): 23-26.

[3]魏唯, 欧阳丹彤, 吕帅, 等. 动态不确定环境下多目标路径规划方法[J]. 计算机学报, 2011, 34(5): 836-847.

WEI Wei, OUYANG Dan-tong, LÜ Shuai, et al. Multiobjective Path Planning Under Dynamic Uncertain Environment[J]. Chinese Journal of Computer,2011, 34(5): 836-847.

[4]魏唯, 欧阳丹彤, 吕帅. 一种实时多目标路径规划方法[J]. 计算机科学, 2010, 37(7): 236-241.

WEI Wei, OUYANG Dan-tong, LÜ Shuai. Real-Time Multiobjective Path Planning[J]. Computer Science,2010, 37(7): 236-241.

[5]郭季, 高博. 多目标路径规划方法的研究[J]. 自动化仪表, 2010, 31(7): 8-12.

GUO Ji, GAO Bo. Research on the Method of Path Planning for Multi-Targets[J]. Process Automation Instrumentation, 2010, 31(7): 8-12.

[6]TALREJA S. Transforming the Concept of Double Bridge Experiment[J]. International Journal of Scientific Engineering and Technology(S2277-1581), 2012, 1(4): 107-110.

[7]蒋里强, 高建军. 装备维修保障的多目标优化模型研究[J]. 现代防御技术, 2012, 40(1): 150-153.

JIANG Li-qiang, GAO Jian-jun. Research on Multi-Objective Optimization Model of Equipment Maintenance Support[J]. Modern Defense Technology, 2012, 40(1): 150-153.

[8]肖天国,符卓.基于遗传算法的联合路径优化[J].中国科技论文在线,2008, 3(10): 720-724.

XIAO Tian-guo, FU Zhuo. Optimizing Route of Muti-Modal Transportaion Based on Genetic Algotithm[J]. Sciencepaper Online, 2008, 3(10): 720-724.

[9]姚跃亭, 赵建军, 杨利斌, 等. 发射与制导分离的编队协同防空目标分配决策[J]. 现代防御技术, 2013, 41(1): 75-81.

YAO Yue-ting, ZHAO Jian-jun, YANG Li-bin, et al. Decision Making on Weapon Target Assignment with Separated Guidance and Fire in Coordinated Air Defense[J]. Modern Defense Technology, 2013, 41(1): 75-81.

[10]DORIGO M, MANIEZZO V, COLORNI A. Ant System: Optimization by a Colony of Cooperating Agents[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B, 1996, 26(1): 29-41.

[11]SHWETA K. An Experimental Study of Ant System for Solving Traveling Salesman Problem[J]. International Journal of Emerging Technology and Advanced Engineering, 2013, 3(7): 648-650.

[12]RAGHAVENDRA G S, KUMAR P. A Note on the Parameter of Evaporation in the Ant Colony Optimization Algorithm[J]. International Mathematical Forum, 2011, 6(34): 1655-1659.

Ant Colony Optimization Based Solution for Generalized Extended Double Bridge Experiment

SUN Ting1,SUN Ye1, XIANG Xin1, XU Yun-shan1, ZHANG Yuan-gui2

(1.Air Force Engineering University,Shaanxi Xi’an 710038, China;2.PLA,No.95810 Troop,Meteorological Observatory, Beijing 100076, China)

Abstract:On the basis of extended double bridge experiment, a generalized extended double bridge problem, which considers path length and several kinds of edge cost are proposed. And it is a basic model of multiple criterion decision. An ant colony optimization based method for multiple criterion decision is proposed. This method models this problem with edge cost matrix and objective function and associate them with pheromone. The simulation results show that this method can solve generalized extended double bridge problem effectively through a reasonable set of parameters, and can also apply to extended double bridge experiment. This experiment proves that ant colony optimization has a good guidance for multiple criterion decision.

Key words:multiple criterion decision; extended double bridge experiment; ant colony optimization

中图分类号：TP391.9

文献标志码：A

文章编号：1009-086X(2015)-05-0242-05

doi:10.3969/j.issn.1009-086x.2015.05.039

通信地址：038399山西省朔州市怀仁县亲和乡清水河村付1号E-mail：344578382@qq.com

作者简介：孙婷(1989-)，女，浙江湖州人。硕士生，主要研究方向为认知无线电、智能算法。

基金项目：国家自然科学基金(61372167)

*收稿日期：2014-05-24；修回日期：2014-08-22