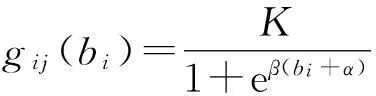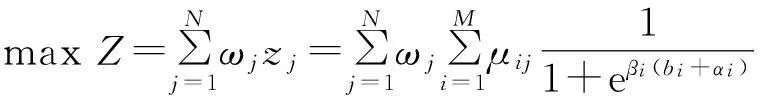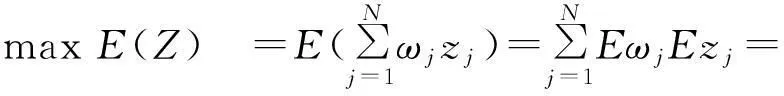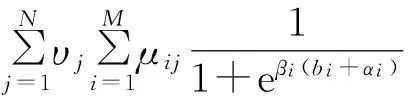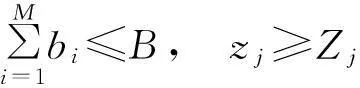不确定条件下武器装备体系发展规划模型*1



不确定条件下武器装备体系发展规划模型*1

刘旭，李为民，宋文静

(空军工程大学 防空反导学院，陕西 西安710051)

摘要：不确定条件下的武器装备体系发展规划是考虑形势变化所带来未知影响下的武器装备规划研究。建立了确定性条件下的武器装备体系发展规划模型，其中引入了Logistic函数反映投入资金与武器能力值之间的映射关系；用证券市场风险投资理论阐述了武器装备发展规划中的不确定性；利用Markowitz理论建立了不确定条件下的武器装备体系发展规划模型；通过某侦察预警监视体系建设规划案例，验证了所建模型和算法的有效性。

关键词：不确定条件；武器装备体系；发展规划模型；投入资金；武器能力值；Logistic；Markowitz

0引言

武器装备体系发展规划是武器装备建设的重要环节，是决策者基于作战背景、能力需求和资源约束等条件，寻求待规划武器装备之间的最佳发展方案，使得武器装备体系整体军事价值达到最大的决策过程[1]。武器装备体系发展规划决定武器装备的发展方向和规模，直接影响军队未来战斗力，具有重要研究意义。

不确定条件下的武器装备体系发展规划是指在未来战略走势不确定条件下规划武器装备体系的过程。在未来战场中，战略走势的变化会导致规划因子间权重系数的变化，在考虑这一情况下，如何进行武器装备体系发展规划，是值得研究的问题。

目前，已有文献针对武器装备体系发展规划方面的研究，主要集中在3个方面：武器装备体系能力需求分析，武器装备体系作战效能评估，武器装备体系结构优化设计，见文献[2-8]。已有文献在规划模型探索、具体问题分析上做了大量工作，但在考虑不确定条件下进行武器装备体系发展规划这一问题上，目前仍未有公开文献。

本文结合武器装备发展规划实际，引入了Markowitz理论解决了不确定条件下的武器装备体系发展规划问题。所建模型可为相关问题规划和论证提供决策支持。

1武器装备规划问题描述

武器装备规划是一个复杂的系统工程，要考虑能力需求、能力冗余和缺失、经费约束、与其他装备协同、发展时间及数量等问题，这些问题在文献[2-8]中有一定程度的描述和研究。为了简化研究问题，本文精简了武器装备规划的规划目的和规划约束。在这一前提下，对武器装备规划问题的分析如下：

武器装备规划的目的是追求最大的武器装备体系总军事价值。武器装备体系一般由M项武器系统组成，每项武器系统均可提供一种以上的作战能力。军事价值可以看成N项作战能力的集成，每项作战能力需求也均由一种以上的武器系统共同满足。两者关系见图1。在满足经费、能力、 型号等约束条件的情况下，如何确定武器装备体系的发展方案，才能使得体系总军事价值达到最大。

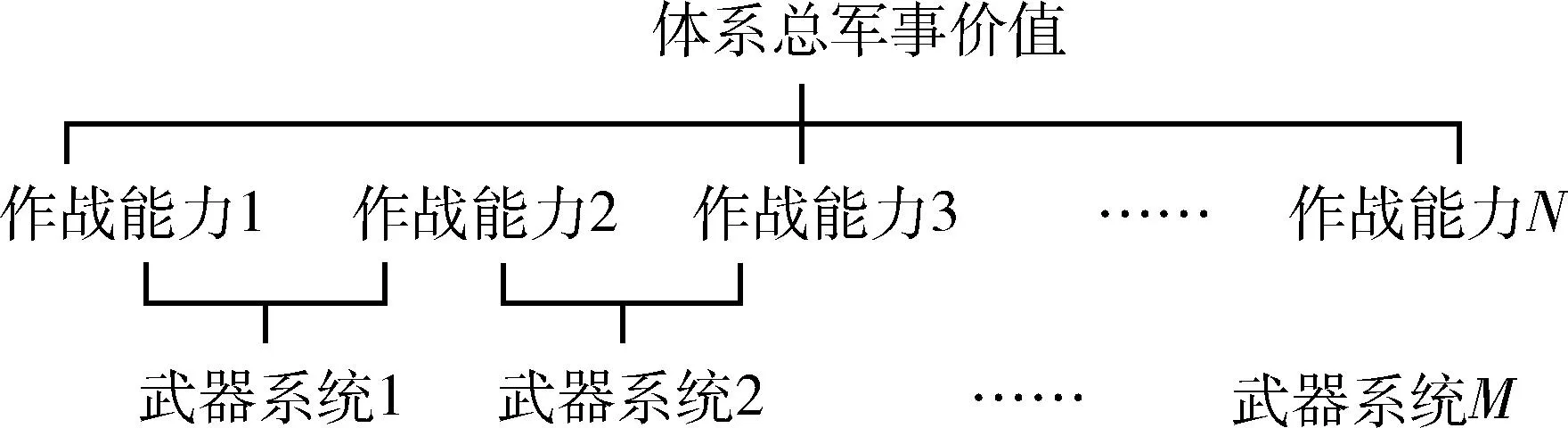
图1　军事价值效益与武器系统的拓扑关系Fig.1　Relationship between military value　　　and weapon system

2确定性情况下的规划模型

不考虑战略走势变化的情况下，建立武器装备体系发展规划模型：

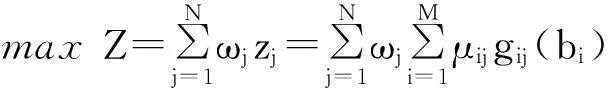
(1)

s.t.

(2)

zj≥Zj，

(3)

(4)

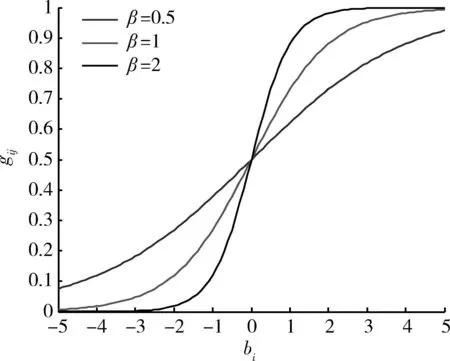
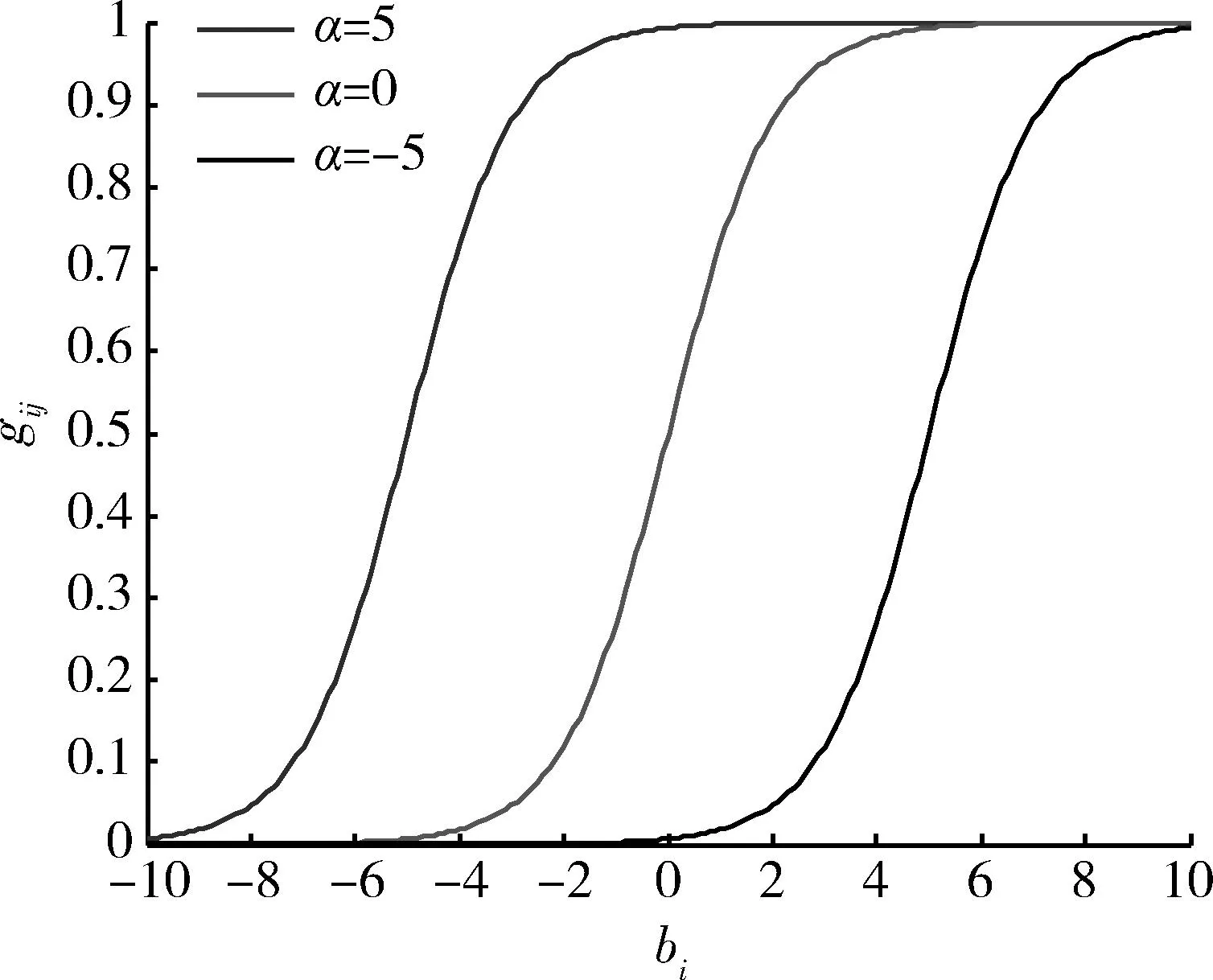
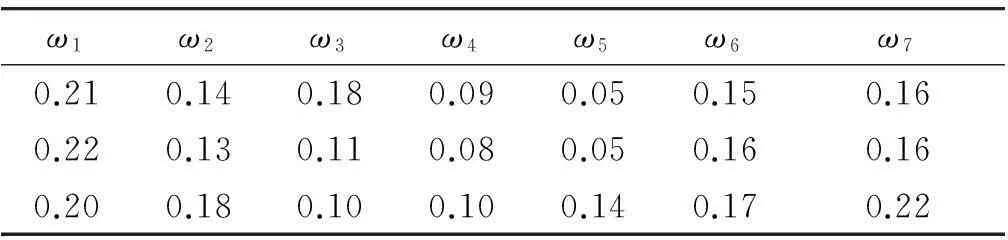
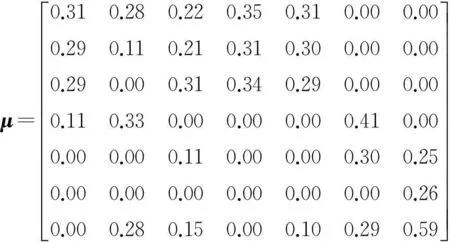
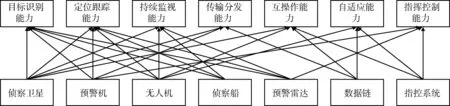
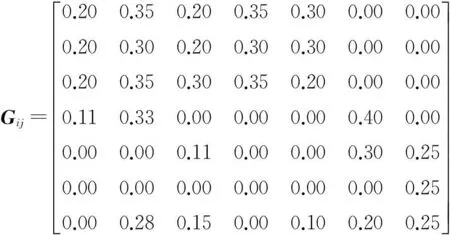
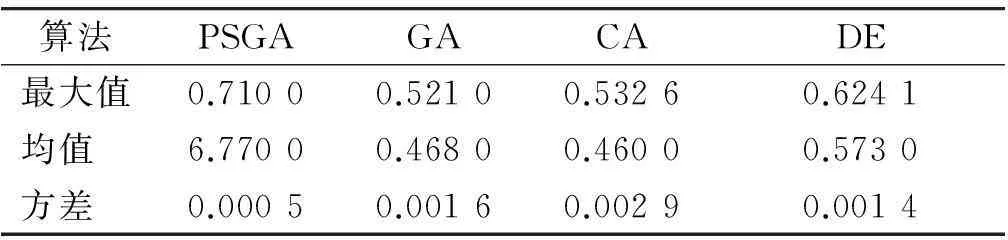
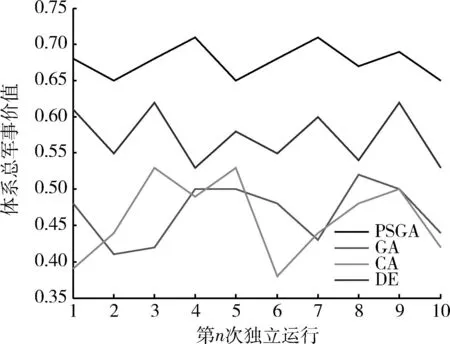
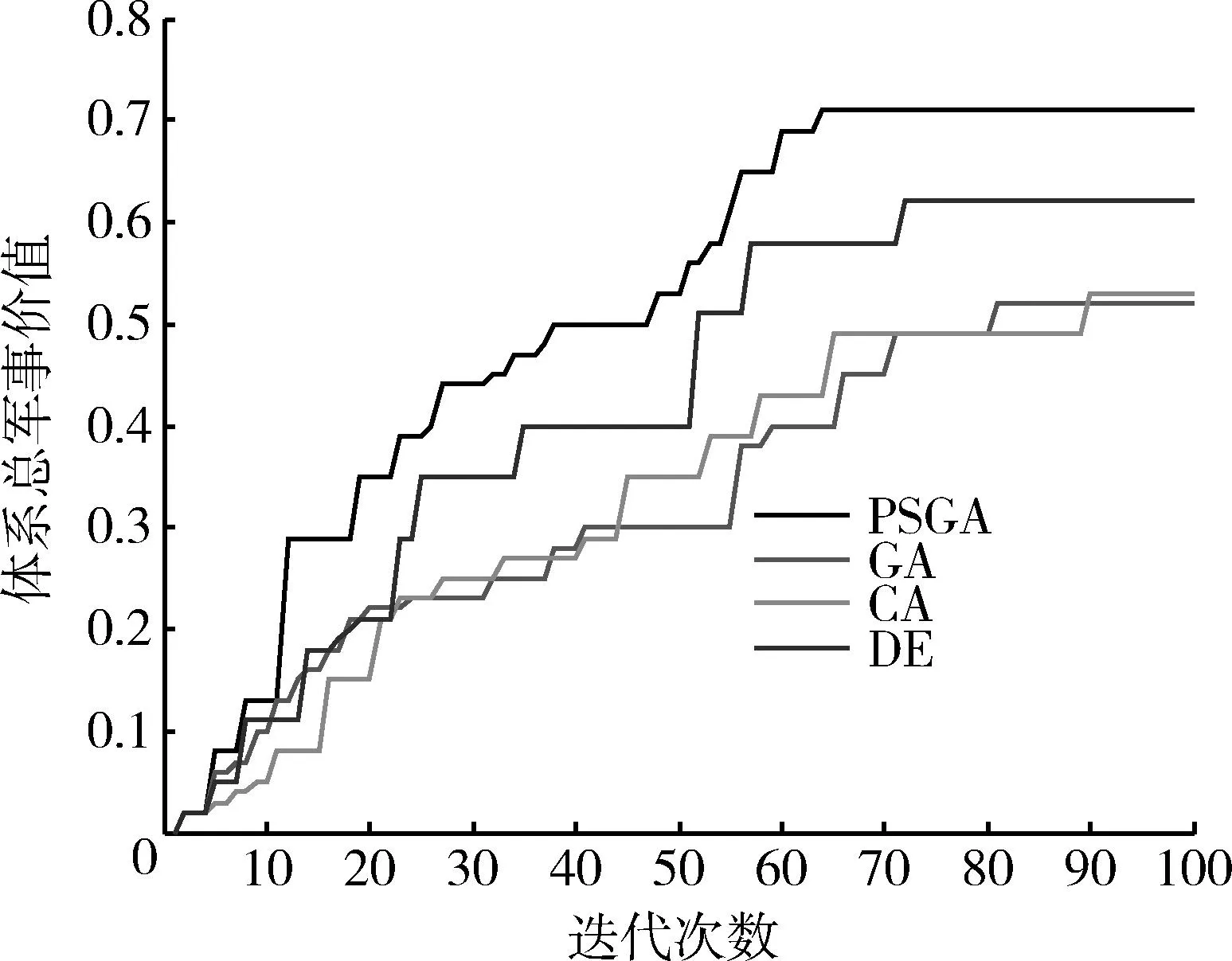
gij(bi)>Gij，0

(5)

式(1)代表体系发展规划目标为体系总军事价值达到最大。其中Z为体系总军事价值;ωj为第j能力在体系总军事价值中的权重；zj为体系具备的第j项能力；μij为第i项武器对第j项能力贡献系数；gij(bi)为第i项武器投入bi资金后拥有的第j项能力值；bi为对第i项武器投入的资金；N为需要满足的能力数；M为体系中包含的武器数。

式(2)代表武器装备体系发展规划方案的总费用要小于B，B为方案的经费约束。

式(3)代表体系的第j项能力zj需要满足最低需求Zj，Zj为体系的子能力约束。

式(5)代表第i项武器的第j项能力值要大于Gij，Gij为武器的子能力约束。

gij(bi)为反映投入资金与武器能力值映射关系的函数，在这里采用Logistic函数。Logistic函数的曲线特性可以描述为：当曲线的自变量过低或过高时，函数值变化率趋向于0。而当自变量取值在适当范围时，曲线的函数值具有较大的变化率。这与武器装备投入费用及所带来能力增幅效益的关系是一致的，当投入费用过低或过高时，武器的能力增幅率都较低，而当投入资金在一定区间时，武器形成的能力增幅率是较大的。Logistic函数的基本形式由式(6)给出[10]：

(6)

式中：K为调整因子；α为位移因子；β为压缩因子。3类因子取值不同的情况下Logistic函数的曲线如图2～4所示。

图2　K=1，K=3，K=5情况下Logistic函数曲线图　　(α=0，β=1)Fig.2　Logistic function graph at K=1,3,5(α=0, β=1)

图3　β=0.5，β=1.0，β=2.0情况下Logistic　　函数曲线图(K=1，α=0)Fig.3　Logistic function graph at β=0.5，β=1.0，　　β=2.0(K=1，α=0)

图4　α=5，α=0，α=-5情况下Logistic函数　　曲线图(K=1，β=1)Fig.4　Logistic function graph at α=5，α=0，　　α=-5(K=1，β=1)

为便于对结果进行比较分析，体系综合军事价值Z需处于[0,1]之间，对gij(bi)进行归一处理，令K=1，则0≤gij(bi)≤1。通过调整α和β，可以得出满足不同武器型号投入费用与能力效益关系的函数。

目标函数式(1)可以表示为

(7)

3Markowitz理论

Markowitz理论是美国经济学家Markowitz于1952年创立的针对证券投资的理论，主要说明“如何衡量投资收益与投资中存在的风险、如何组合自己的资金获得最大收益”等问题。该理论多年来在国内外证券投资风险管理中得到广泛应用和长足发展，被认为是现代投资组合理论的里程碑[11]。

Markowitz理论提出，用E(R)来度量投资收益大小，用D(R)来度量投资存在的风险[12]。基于这一理念，在决策者考虑一定风险下追求最大投资收益的情况下，组合投资决策模型则可以表示为

(8)

s.t.D(R)

(9)

式中：maxE(R)代表投资者的目的是追求投资收益最大；D(R)

4不确定性情况下的规划模型

武器装备体系规划从某一角度可以看成是用时间、人力、财力对武器装备发展的一个投资，与证劵投资有相似之处。因此，将Markowitz理论应用于武器装备体系规划，可以很好地解决武器装备体系规划中的不确定性问题。假定战略走势的不确定会带来能力权重的变化，则式(1)中ωj为随机变量，E(ωj)=υj。将投入资金后拥有的能力组合看成投资组合，将能力权重看成收益率，结合Markowitz理论，则不确定性情况下的武器装备发展规划模型为

(10)

s.t.

gij(bi)>Gij，0

(11)

5案例分析

通过对案例的发展规划过程进行研究，可分析所建模型的有效性。假定当前需要规划发展某侦察预警监视体系，该体系的能力需求内容、可选装备类型、装备与能力之间的映射关系如图5所示。

(1) 参数设定

由图5可知，N=7，M=7。假设采集了近3年的ω取值，见表1。

表1　近3年ω参数设定

则υ=(0.21,0.15,0.13,0.09,0.08,0.16,0.18)。令

图5　决策变量-能力需求之间的关系Fig.5　Relationship between decision variable and capability requirement

表和参数设定

(2) 算法验证

在这里采用改进的遗传算法对模型进行验证。在文献[13]中，基于捕食搜索策略(predatory search,PS)对遗传算法(genetic algorithm,GA)进行了改进，具体思想为：将捕食搜索策略应用到遗传算法中，克服遗传算法局部搜索能力弱的问题。首先以较大的交叉概率和较小的变异概率进行全局搜索；一旦发现一个较优解，则改为以较小的交叉概率和较大的变异概率进行局部搜索； 如果在一定次数

的搜索过程中较优解得不到改善，则恢复以较大的交叉概率和较小的变异概率进行全局搜索。基于捕食搜索策略的遗传算法(PSGA)过程如图6所示。

图6　PSGA算法流程图Fig.6　Flow diagram of PSGA arithmetic

为了便于比较，这里采用PSGA算法与传统遗传算法(GA)、蚁群算法(ant colony algorithm, CA)、微分进化算法(differential evolution algorithm,DE)，分别对这一案例进行求解。根据文献[14-16]，各算法的参数设置见表3。

表3　PSGA/GA/CA/DE参数设置

首先分析算法的求解稳定性。分别对4种算法独立运行10次，获得每次运算的体系总军事价值最优值，见图7。对10次运算所得最优值的最大值、均值和方差进行计算，结果见表4。可见，PSGA的方差值是4类算法中最小的，代表PSGA求解稳定性最好。

表4　PSGA/GA/CA/DE独立运算结果

图7　PSGA，GA，CA，DE求解稳定性比较Fig.7　Stability comparison among PSGA,GA,　　　CA, and DE

然后分析算法的求解效率性。将4类算法10次独立运行中得出最大体系总军事价值的求解过程

提取出来进行比较，见图8。可见，在收敛速度方面，PSGA在第64次达到收敛，而GA，CA，DE 3类算法分别在81，90，72次才达到收敛。而在最优值的搜寻上，PSGA，GA，CA，DE 4类算法分别是0.710 0，0.521 0，0.532 6，0.624 1。所以，无论是收敛速度，还是最优值的搜寻能力，PSGA均优于其他3类算法，PSGA具有更高的求解效率性。

图8　PSGA，GA，CA，DE求解效率性比较Fig.8　Efficiency comparison among PSGA,　　　GA, CA, and DE

(3) 规划方案分析

分析4类算法所得的最优发展规划方案，见表5。可知4类算法都倾向于优先发展预警机、侦察卫星2类武器装备。并且PSGA算法在预警机装备上投入资金最多，所得体系总军事价值也最大。规划方案结果的得出与前面设置的参数有关，实际操作时应根据作战实际严格设置参数，才能得出有效的结论。

表5　最优发展规划方案

6结束语

将Markowitz理论应用于武器装备体系规划，既为Markowitz投资组合理论开拓一个新的应用领域，也为武器装备体系发展规划找到一个新的定量决策模型，且较好地解决了战略走势变化带来的不确定影响这一问题，所建模型可为类似问题规划提供模型参考。

本文从理论和方法的角度对武器装备体系规划做了探索。下一步的研究应包括：如何用数学方法科学精确地描述军事价值；如何建立可操作性强、更反映规划实际的数学模型；如何确定投入资金与武器能力值之间映射关系的函数——即文中的Logistic函数中的变量系数；如何综合考虑并描述形势变化带来的其他不确定影响因素；如何构建包含更多规划目标和约束条件的模型；如何改进算法以实现更快更稳的寻优。

参考文献：

[1]李仁传，张合勇，殷燕. 对武器装备体系结构优化几个基本问题的理性认识[J]. 军事运筹与系统工程，2011，25(2)：5-10．

LI Ren-chuan，ZHANG He-yong，YIN Yan. An Understanding on Several Basic Problems of Weapon System of System Structural Optimization [J]. Military Operations Research and Systems Engineering，2011，25(2)：5-10．

[2]周宇，谭跃进，姜江，等. 面向能力需求的武器装备体系组合规划模型与算法[J]. 系统工程理论与实践，2013，33(3)：809-816．

ZHOU Yu，TAN Yue-jin，JIANG Jiang，et al. Capability Requirements Oriented Weapon System of Systems Portfolio Planning Model and Algorithm [J]. Systems Engineering—Theory and Practice，2013，33(3)：809-816．

[3]熊健，赵青松，葛冰峰，等. 基于多目标优化模型的武器装备体系能力规划[J]. 国防科技大学学报，2011，33(3)：140-144．

XIONG Jian，ZHAO Qing-song，GE Bing-feng，et al. Weapon Equipment System-of-Systems Capability Planning Based on Multi-Objective Optimization Model [J]. Journal of National University of Defense Technology，2011，33(3)：140-144．

[4]LEE J，KANG S H，ROSENBERGER J，et al. A Hybrid Approach of Goal Programming for Weapon Systems Selection[J]. Computers and Industrial Engineering，2010，58(3)：521-527．

[5]SNYDER D，MILLS P，RESNICK A C，et a1. Assessing Capabilities and Risks in Air Force Programming[R]. Pittsburgh：RAND Corporation，2009．

[6]STRUBE C M，LOREN J R．Portfolio Influences on Air Force Capabilities-Based Assessment and Capabilities-Based Planning Activities[C]∥Proceedings of the 6th International Conference on System of Systems Engineering，Albuquerque，New Mexico，USA，2011：83-89．

[7]United States Government Accountability Omce. Defense Acquisitions Assessments of Selected Weapon Programs[EB/OL]．[2012-4-18](2014-11-28)．http：//

www.gao.gov/assets/320/317081.pdf．

[8]GREINER M A，FOWLER J W，SHUNK D L，et al．A hybrid Approach Using the Analytic Hierarchy Process and Integer Programming to Screen Weapon Systems Projects[J]．IEEE Transactions on Engineering Management，2003，50(2)：192-203．

[9]张媛，刘文彪，张立民. 基于主客观综合赋权的CGF态势评估建模研究[J]. 系统工程与电子技术，2013，35(1)：85-90．

ZHANG Yuan，LIU Wen-biao，ZHANG Li-min. Situation Assessment Modeling for CGF Base on the Subjective and Objective Integrated Weight [J]. Systems Engineering and Electronics，2013，35(1)：85-90．

[10]刘旭,李为民，吴晓东. 雷达抗干扰性能多层次灰色评估模型研究[J]. 现代防御技术，2011，39(6)：179-184．

LIU Xu，LI Wei-min，WU Xiao-dong. Multilevel Gray Evaluation Model for Radar Antijamming Capability [J]. Modern Defence Technology，2011，39(6)：179-184．

[11]吴晓. Markowitz投资组合理论在房地产投资组合决策中的应用[J]. 深圳职业技术学院学报，2011(1)：36-42．

WU Xiao. Application of Markowitz Portfolio Theory in Real Estate Portfolio Decision [J]. Journal of Shenzhen Polytechnic，2011(1)：36-42．

[12]杨明辉，张智光，任百林，等. Markowitz组合证券投资决策模型的修正[J]. 南京林业大学学报:自然科学版，2005，29(1)：51-54．

YANG Ming-hui， ZHANG Zhi-guang， REN Bai-lin， et al. A Study on Revising Markowitz’s Portfolio Selection Model [J]. Journal of Nanjing Forestry University:Natural Sciences ed， 2005，29(1)：51-54．

[13]刘旭，李为民，宋文静. 考虑发射区部分重叠的防空作战目标分配[J]. 空军工程大学学报：自然科学版，2013，14(6)：30-34．

LIU Xu，LI Wei-min，SONG Wen-jing. Target Assignment of Defense Combat in Overlapping Shooting-Area [J]. Journal of Air Force Engineering University：Natural Science ed，2013，14(6)：30-34．

[14]余家祥，赵晓哲，史红权，等. 基于遗传算法的编队区域防空武器分配方法[J]. 现代防御技术，2013，41(1)：82-87．

YU Jia-xiang，ZHAO Xiao-zhe，SHI Hong-quan，et al. Air Defense Weapon Allocation Method for Warship Task Formation Based on Genetic Algorithm [J]. Modern Defence Technology，2013，41(1)：82-87．

[15]李红亮，宋贵宝，曹延杰. 多反舰导弹攻击多目标协同航路规划[J]. 系统工程与电子技术，2013，35(10)：2013-2019．

LI Hong-liang，SONG Gui-bao，CAO Yan-jie. Cooperative Path Planning of Multiple Anti-Ship Missiles to Multiple Targets [J]. Systems Engineering and Electronics，2013，35(10)：2013-2019．

[16]黄仁全，李为民，周晓光，等. 基于微分进化算法的防空导弹火力分配[J]. 空军工程大学学报：自然科学版，2009，10(5)：41-44．

HUANG Ren-quan，LI Wei-min，ZHOU Xiao-guang，et al. Research on Firepower Distribution Model of Surface to Air Missile Based on Differential Evolution Algorithm [J]. Journal of Air Force Engineering University：Natural Science ed，2009，10(5)：41-44．

Systems Development Planning Model on Weapon System Under Uncertain Conditions

LIU Xu， LI Wei-min，SONG Wen-jing

(AFEU,Air and Missile Defense School,Shaanxi Xi’an 710051,China)

Abstract:The system development planning on weapon system under uncertain conditions is to study weapon system development planning model considering changing conditions. The systems development planning model of weapon system under certain conditions is built; the logistic function is introduced into the model to reflect the mapping relationship between investment funds and weapon capability. The uncertain conditions for the system development planning are explained with securities market risk investment theory. And the model under uncertain conditions is built based on Markowitz theory. The effectiveness of the proposed model and algorithm are demonstrated by a portfolio planning example of intelligence, surveillance, and reconnaissance weapon system.

Key words:uncertain conditions; weapon system of systems; development planning model; investment funds; weapons capability; Logistic; Markowitz

中图分类号：E92；E917

文献标志码：A

文章编号：1009-086X(2015)-05-0026-07

doi:10.3969/j.issn.1009-086x.2015.05.005

通信地址：710051陕西西安长乐东路甲字1号空军工程大学防空反导学院研2队E-mail：liuxu193@126.com

作者简介：刘旭(1987-)，男，湖南湘潭人。博士生，研究方向为作战力量建设。

*收稿日期：2014-12-07；修回日期：2015-03-31