分布式多输入多输出天波超视距雷达海杂波仿真

薛永华 安 昕 王国庆 周 伟 关 键

（1.海军航空工程学院电子信息工程系，山东 烟台264001；2.中国人民解放军海军92277部队，山东 青岛266102）

引 言

分布式多输入多输出（Multiple-Input Multiple-Output，MIMO）体制的采用是天波超视距雷达发展的重要趋势之一［1-2］.强海杂波中海面慢速运动目标的探测是天波超视距雷达探测的重点和难点之一.分布式MIMO天波超视距雷达采用空间分布较广的多个发射站和接收站，多个发射站同时发射正交发射波形，经电离层反射到达目标处，目标散射后，部分散射信号经电离层反射到达各接收站，接收站通过匹配滤波分离出不同发射信号，最后联合处理完成目标的探测.与传统的（准）单基地天波超视距雷达相比，分布式MIMO天波超视距雷达由于收发站空间间隔较大，从不同角度观测目标，可获得空间分集增益；采用多种发射波形还可获得波形分集增益，在抗目标雷达散射截面积（Radar Cross Section，RCS）起伏、动目标检测等方面有巨大的优势，给强海杂波中海面慢速运动目标的探测提供了新的思路.与此同时，分布式MIMO天波超视距雷达的海杂波特性也更加复杂，不同的收发通道，几何关系不同，海杂波Bragg峰的位置也不同；电波传播路径上电离层状态不同，对海杂波的调制效应也不同；若采用频率正交发射波形，频率间隔较远时频率也会对海杂波特性造成显著的影响.

从海杂波形成的物理机制出发，深入分析分布式MIMO天波超视距雷达的海杂波特性，建立相应的模型并对其进行仿真，对分布式MIMO天波超视距雷达的海面目标检测技术，解决天波超视距雷达强海杂波中慢速目标的检测问题有着重要的意义.

高频雷达海杂波形成机理的研究，最早可追溯到1955年D.D.Crombie针对试验数据用Bragg谐振散射机理来对无线电波与海浪一阶作用的成功解释［3-4］.1972年，D.E.Barrick采用边界微扰法定量解释了随机海面上高频电磁波的散射机理，给出了单位面积下的一阶和二阶海杂波归一化散射截面积表达式，其中一阶表达式可适用于单基地或者双基地天波和地波雷达的情形，其二阶表达式仅适用于单基地地波雷达的情形［4］.1999年，E.W.Gill对双基地高频电磁波的海面散射进行了理论分析，给出了双基地地波雷达的一阶和二阶海杂波散射截面积表达式［5］，并在此基础上给出了在给定雷达参数情况下，海杂波加噪声时间序列的仿真实现方法［6］.S.Grosdidier等为使散射截面积的计算更加符合实际情况，进一步考虑了整个雷达系统的特性，包括天线方向图、距离衰减、接收信号的多普勒处理等因素，并与实测数据对比，取得了较好的效果，但其应用背景仍然是地波雷达的情形［7］.目前，针对天波超视距雷达海杂波的仿真研究，均以（准）单基地为应用背景［8-9］，而对于分布式MIMO天波超视距雷达而言，每个收发通道均需按成双基地的情形处理，故上述仿真方法均不适用.杨龙泉等分析了天波反射／地波绕射组合模式下一阶海杂波的产生机制、展宽原理，导出了一阶海杂波频移、展宽计算公式［10］，对分布式MIMO天波超视距雷达海杂波的仿真具有一定的借鉴意义.

针对分布式MIMO天波超视距雷达的情形，采用数字射线追踪计算各收发通道相对于观测海面的入射和返回散射的方位角和俯仰角，导出各收发通道双基地一阶和二阶海杂波归一化散射截面积表达式；在与收发传播路径的多普勒传递函数相卷积后，结合雷达方程得到接收端的海杂波功率谱密度；最后，根据该功率谱密度仿真接收端海杂波加噪声的随机时间序列，并对其特性进行简要分析.

1 归一化海杂波雷达散射截面积

分布式MIMO天波超视距雷达的多个发射站和接收站空间分布较广，如图1所示.每个收发通道的海杂波均为双基地散射，不同收发通道与关心探测区域的几何关系不同，不同收发通道中电磁波通过的电离层区域不同，这使得关心的海面上，不同收发通道的电磁波入射和返回散射的几何关系不同.

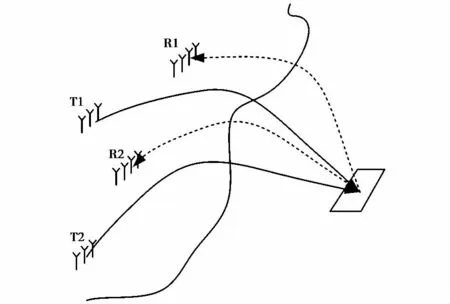
图1 分布式MIMO天波超视距雷达示意图

对于其中任意一个收发通道，采用数字射线追踪方法可以得到其发射站到观测海面，观测海面到接收站的传播路径，这里采用文献［11］中的射线追踪方法，不再赘述.根据传播路径可以得到该通道入射方向和返回散射方向的方位和俯仰角，进而得到入射电波擦地角Δi，返回散射电波擦地角Δs及半双基地角φ0，如图2所示.因此，该通道双基地Bragg谐振条件为［10］

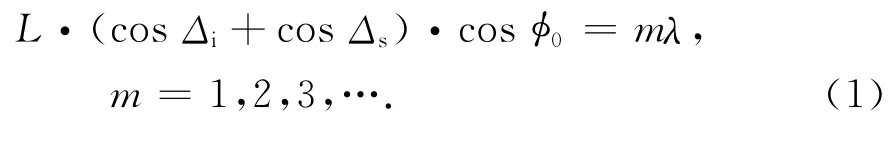
式中，L，λ分别表示海浪波长和电波波长.

高频电磁波与海浪一次作用后的散射回波为一阶海杂波（m＝1），此时有

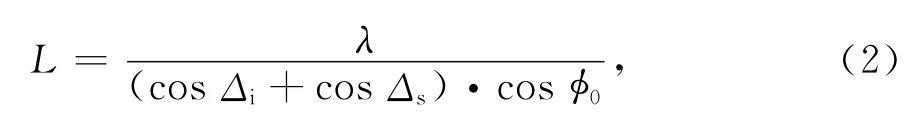
即只有满足式（2）的海浪波长才会产生一阶相干散射.对于重力波，满足表示特征速度，g表示重力加速度，由重力波产生的多普勒频移为

对应的多普勒角频率

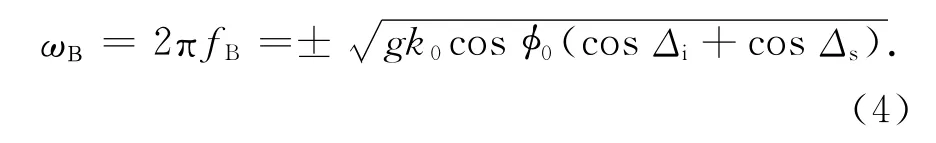
式中：k0＝2π／λ表示雷达发射电磁波波数；±号表示沿着双基地角平分线朝向雷达与背离雷达的重力波产生的正负多普勒频率偏移.高频无线电波与海浪的一阶作用会在回波的多普勒频谱中成对地产生正负一阶Bragg峰，其位置由式（4）确定.

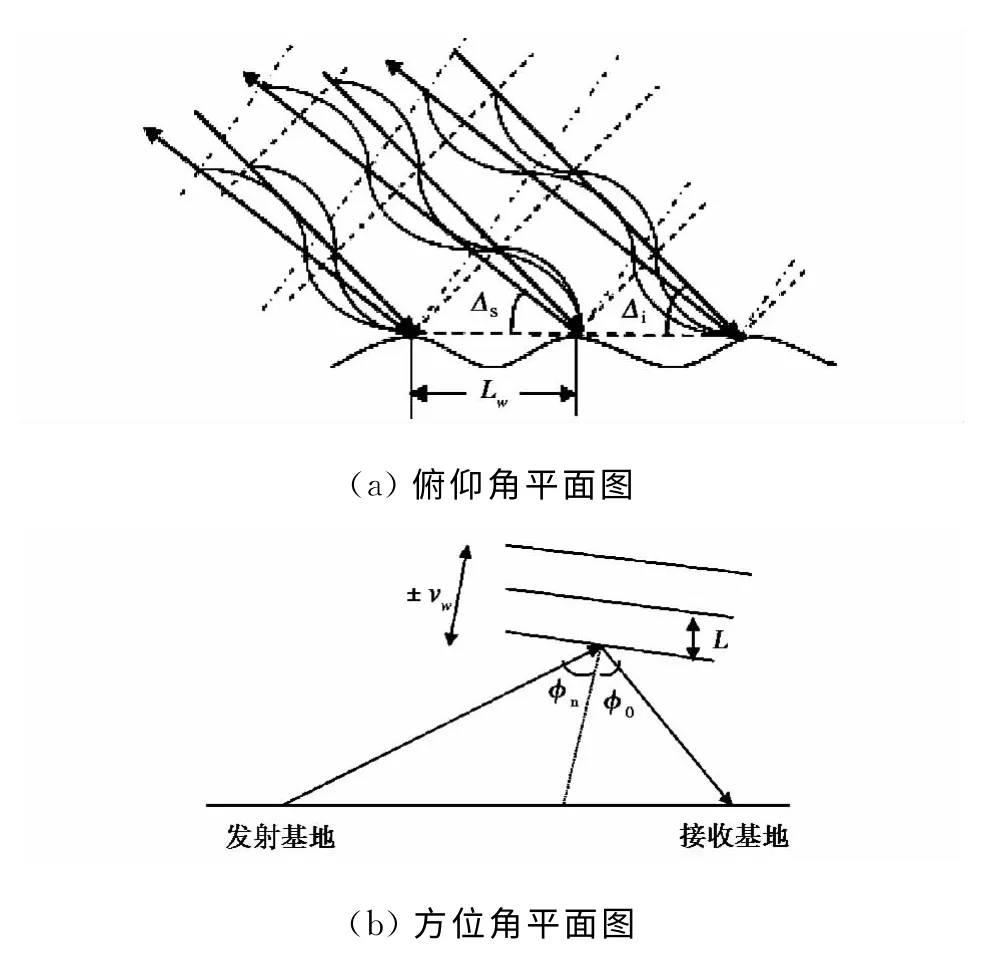
图2 双基地一阶Bragg散射机理

考虑双基地天波雷达目标探测的几何关系，用上述计算得到的一阶Bragg峰对双基地地波雷达的一阶和二阶海杂波单位面积RCS多普勒谱［5］进行修正，得

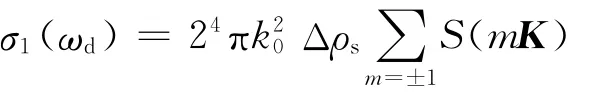
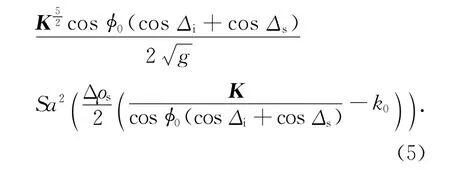
式中：Δρs表示雷达的距离分辨力；K，S（mK）分别表示海洋波数和其海洋波高谱.

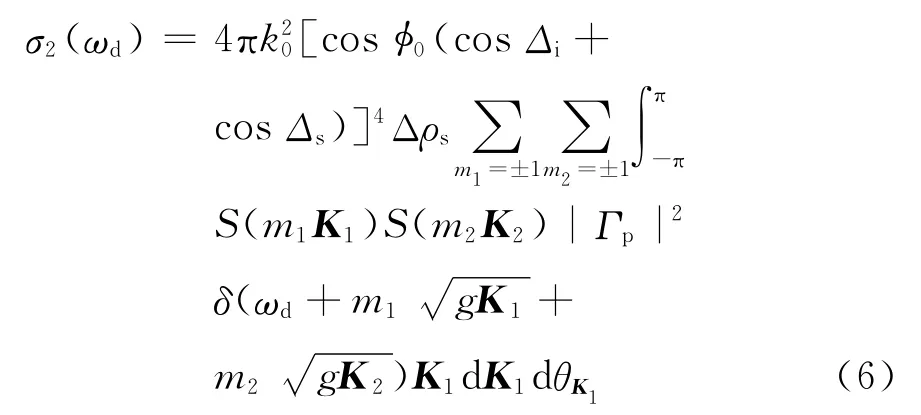
式中：K1，S（m1K1）分别表示一阶海洋波数和其海洋波高谱；K2，S（m2K2）分别表示二阶海洋波数和其海洋波高谱；θK1表示波矢量K1的方向角；ΓP表示耦合系数，由电磁耦合系数ΓEP和流体动力学分量耦合系数ΓH构成，即

得到该通道双基地海杂波归一化散射截面积为

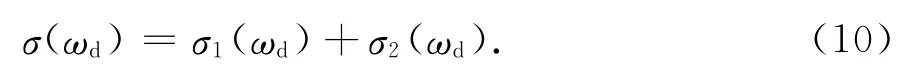
2 雷达接收的海杂波功率谱密度

根据雷达方程，对于分布式MIMO天波超视距雷达的任意一个收发通道，雷达接收机接收到的海杂波功率谱密度为

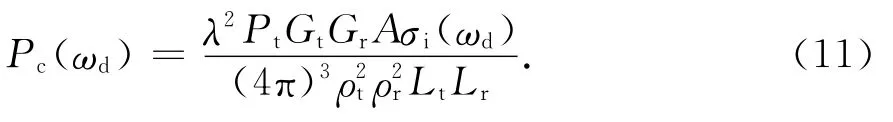
式中：Pt表示发射功率；Gt表示发射天线增益；Gr表示接收天线增益；表示分辨单元面积，ΔR表示雷达距离分辨力，表示接收天线3dB波束宽度；ρt表示发射机到目标传播路径的几何距离；ρr表示接收机到目标传播路径的几何距离；Lt表示发射机到目标的电波传播损耗；Lr表示接收机到目标的电波传播损耗；σi（ωd）表示通过电离层后的海杂波单位面积RCS多普勒谱，其表达式为

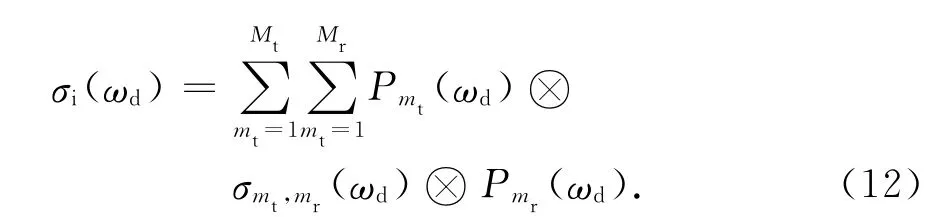
式中：⊗表示卷积；mt＝1，2，…，Mt；mr＝1，2，…，Mr；Mt，Mr分别表示发射和接收传播模式个数；Pmt（ωd）表示第mt个接发射传播模式的多普勒扩展因子；Pmr（ωd）表示第mr个接收传播模式下多普勒扩展因子；σmt，mr（ωd）表示第mt-mr个收发通道的归一化RCS多普勒谱.扩展因子的计算可根据电离层信道的广义功率谱函数［11］计算得到，以第mt个接发射传播模式为例，可表示为

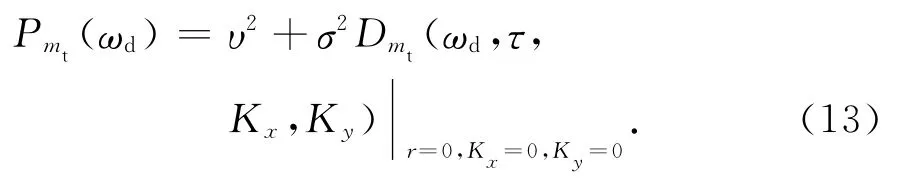
式中，Dmt（ωd，τ，Kx，Ky）表示第mt个接发射传播模式的广义功率谱密度.

3 海杂波加噪声时间序列

对于高频雷达而言，外部噪声是时刻存在的.无目标时，雷达接收机接收到的信号是海杂波加外部噪声.外部噪声一般可认为是白噪声，其功率谱密度为

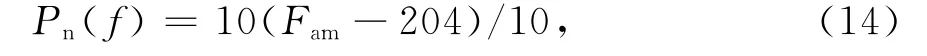
式中：Fam表示等效外部噪声系数；204是单位带宽内接收系统的热噪声系数.

至此，雷达接收机接收到的海杂波和噪声的功率谱密度已得到.该功率谱对应的随机时间序列信号才是雷达接收机实际接收到的信号.根据文献［6］，对于带宽为B，已知功率谱密度的一维平稳高斯过程，其时间序列为

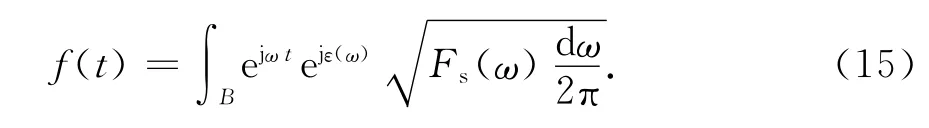
式中：ω∈［-B，B］；ε（ω）为服从［0，2π］均匀分布的随机过程；Fs（ω）表示功率谱密度.对于海杂波Fs（ω）＝Pc（ω），相应地，f（t）＝c（t）；对于噪声Fs（ω）＝Pn（ω），相应地，f（t）＝n（t）.为方便离散数值计算，采用部分和来逼近f（t）的积分运算，如下式所示

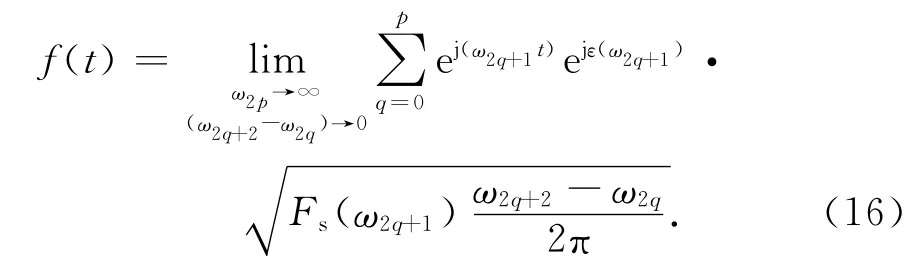
将海杂波和噪声的功率谱密度代入，即可得到海杂波时间序列c（t）和噪声时间序列n（t），两者求和即可得到无目标时雷达接收机的接收信号：

4 仿真流程及结果分析

根据各收发通道的双基地海杂波及噪声功率谱，进行仿真计算，即可得到各收发通道的海杂波加噪声随机时间序列.这里针对其中一个通道的海杂波仿真，将仿真过程梳理如图3所示，其它通道类似.首先，根据电离层参数、收发站位置和观测位置，设定发射频率，进行射线追踪计算，得到入射和返回散射俯仰角和半双基地角；其次，设定海面参数，根据式（10）计算该通道双基地海杂波归一化散射截面积；然后，将通道收发参数及收发路径的多普勒扩展及损耗因子代入式（11）计算接收海杂波的功率谱密度；最后，查表得到噪声功率系数，仿真计算海杂波加噪声的随机时间序列.

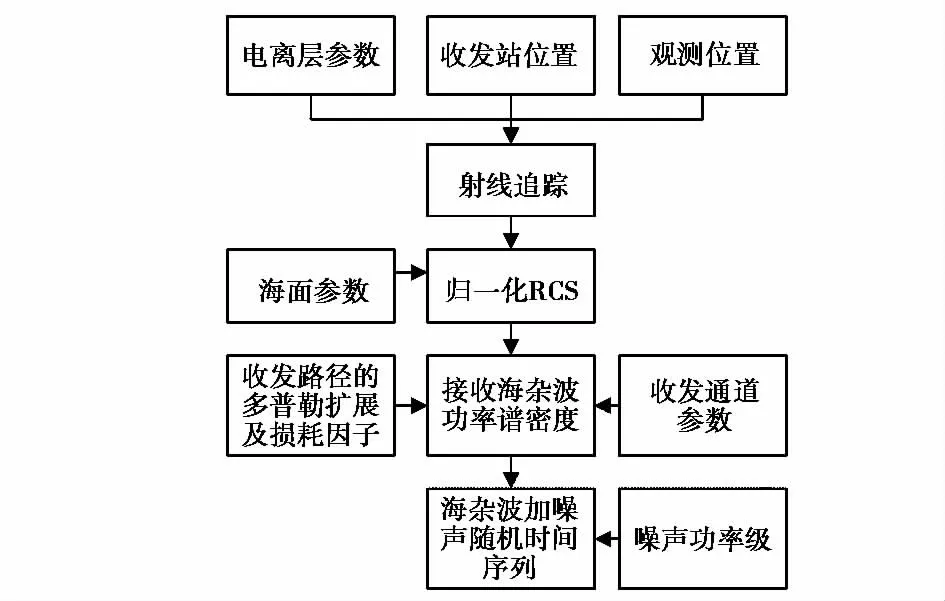
图3 一个收发通道的海杂波仿真流程图

从仿真过程可知，影响海杂波和噪声特性的因素主要来自三个方面：一是雷达系统参数，包括工作频率、不同收发通道的双基地角及收发波束的俯仰角等；二是电离层信道，包括电离层信道电子浓度起伏、运动等；三是海面状况，包括海面风速、风向等.其中海面状况的影响与地波雷达的情形［12］类似，不再赘述，下面主要分析前两个因素对海杂波功率谱的影响，并简要分析杂波和噪声时间序列的特性.

4.1 海杂波和噪声功率谱特性分析

1）雷达系统参数的影响

分布式MIMO天波超视距雷达不同的收发通道的多普勒谱与其发射频率，和关心海域所成的双基地角及收发波束的俯仰角等因素有关.这些因素造成不同通道多普勒谱的多样性，进而带来分集增益.

雷达系统参数设置如下：每个发射通道发射功率Pt＝15kW，发射天线增益Gt＝9dB，接收天线增益Gr＝10dB，带宽B＝20kHz，对应距离分辨力ΔR＝15km，接收天线3dB波束宽度3°，ρt＝ρr＝2 000km，Lt＝Lr＝3dB，风速为15m／s，风向为0°，海浪谱采用JONSWAP谱，发射波形为连续波，重复频率为10Hz，相干积累时间为25.6s.图4为不同雷达工作频率时，一个收发通道海杂波和噪声的功率谱，其中实线、虚线、点画线对应的工作频率依次是5、12、18MHz，这里半双基地角为10°.根据文献［13］中提供的表格查得三个工作频率对应的等效外部噪声系数分别为30、40、60dB，噪声功率级分别为-174、-164、-144dB.由图可知，雷达工作频率改变时Bragg峰的幅值变化不大，不同的频率Bragg峰的位置不同，这由式（3）可以看出，Bragg峰的位置与波长的平方根成反比.一般而言，高的工作频率上，等效外部噪声系数较低，噪声功率较低，杂噪比较高，更有利于杂波的抑制及目标的检测.

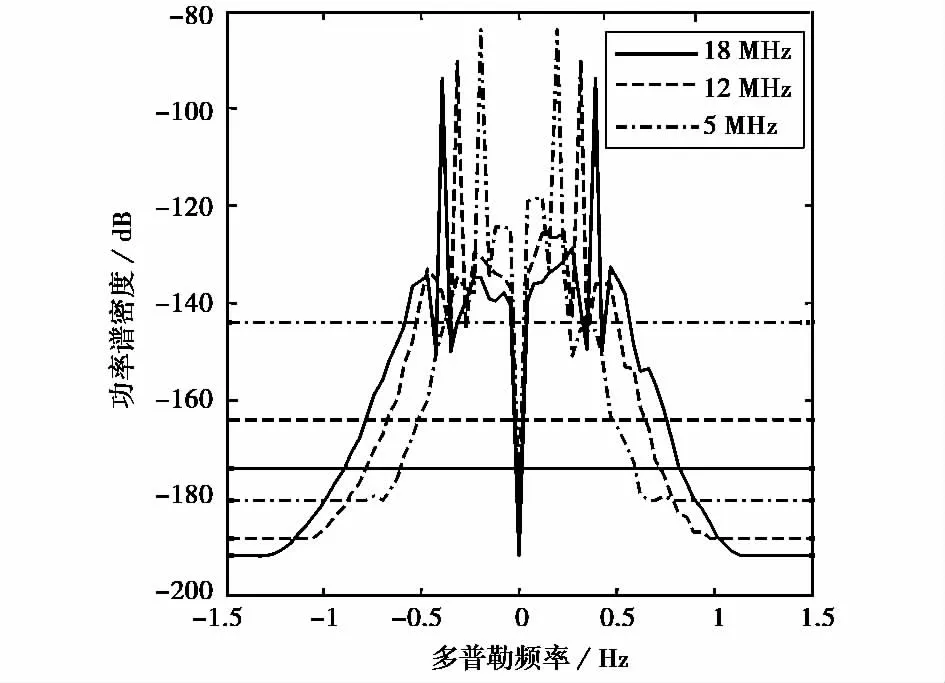
图4 雷达工作频率对功率谱的影响

雷达收发波束的俯仰角对海杂波功率谱的影响如图5所示，为方便分析这里假设收发波束俯仰角相同，工作频率为12MHz.从图上来看，海杂波功率谱随俯仰角余角（即擦地角）在5°变化到20°几乎不变，当擦地角取35°时，Bragg峰的位置有小的偏移.另外，不同擦地角的海杂波多普勒峰值的变化不大，只有几个dB.当然，由式（3）可知Bragg峰的位置随擦地角的变化还与半双基地角有关，这里预设半双基地角为10°，当半双基地角更小时，仿真情形类似，当半双基地角增大到约25°时，多普勒谱几乎不随俯仰角的变化而变化.这说明，在天波雷达探测采用的5°～35°的擦地角范围内，海杂波的多普勒谱对擦地角不敏感.

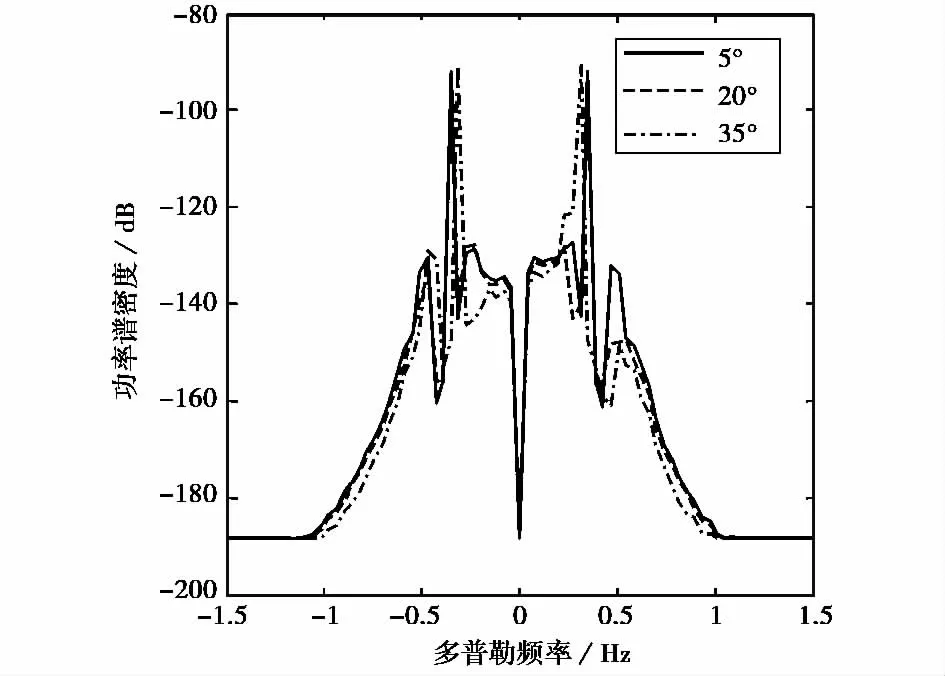
图5 收发波束的俯仰角对功率谱的影响

雷达双基地角对海杂波功率谱的影响如图6所示，这里雷达工作频率为12MHz.从图中可以看出，随着半双基地角的增大，一阶Bragg峰高度变化不大，位置逐渐向零频靠近，这是由于Bragg峰的位置与半双基地角余弦平方根的正比关系造成的，见式（3）.

图6 半双基地角对功率谱的影响

2）电离层对海杂波多普勒谱的影响

由本方法计算得到的海杂波谱与文献［11］计算的电离层模型卷积即可得到接收站接收到的海杂波多普勒谱，如图7所示.由图可见，海杂波通过电离层后期多普勒谱明显变宽.当电离层出现多模传播时，且每个传播模式带来的多普勒频移不同时，海杂波的多普勒谱出现重影，有多个一阶峰，如图7所示，在多普勒谱上占据更大片范围，会严重影响目标的检测.

4.2 海杂波加噪声时间序列特性分析

以图4中18MHz对应的海杂波和噪声的功率谱为基础，通过图7中单模传播的电离层后，仿真计算得到海杂波加噪声的时间序列，如图8所示，对其进行傅里叶变换得到图9的结果.由于电离层的作用，海杂波的二阶峰几乎被平滑掉，海杂波的时间序列也出现了一定程度的衰落.

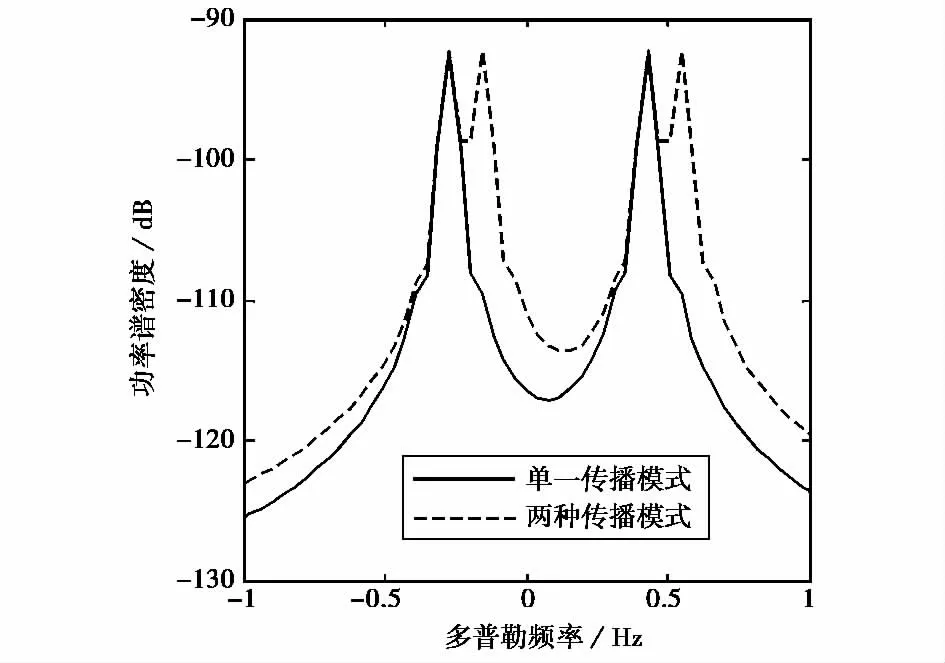
图7 电离层多模传播对多普勒谱的影响

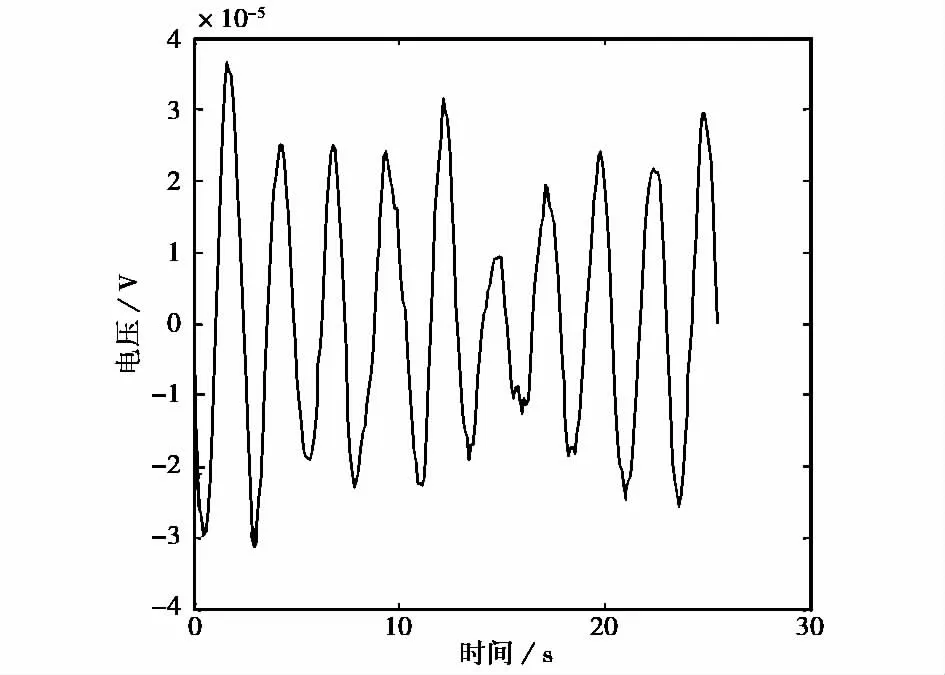
图8 海杂波加噪声时间序列

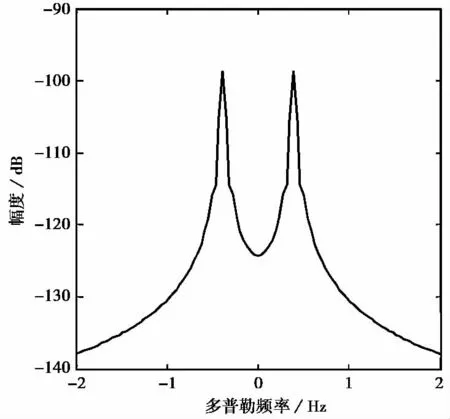
图9 海杂波加噪声的傅里叶谱

5 结 论

针对分布式MIMO天波超视距雷达的情形，采用数字射线追踪计算各收发通道相对于观测海面的入射和返回散射的方位角和俯仰角，导出了各通道单位面积下双基地一阶和二阶海杂波归一化散射截面积表达式；在与收发传播路径的多普勒传递函数相卷积后，结合雷达方程得到了接收端的海杂波功率谱密度；并仿真了接收端海杂波加噪声的随机时间序列.仿真中对影响分布式MIMO天波超视距雷达海杂波的因素考虑较为全面，通用性较好，计算量适中，可方便地用于各种体制的天波超视距雷达海杂波的仿真，以及海杂波抑制的研究.

需说明的是，仿真对发射和接收天线均假设为垂直极化，另外对电离层法拉第效应带来的极化旋转也未加考虑.但现有的天波超视距雷达系统收发天线主要采用垂直极化天线，而由于高频波段电离层法拉第效应导致的极化旋转角度很大且随机性较强，故通常将这一影响按3dB的极化损失处理，故并不影响仿真的适用性.

更精确的天波超视距雷达海杂波仿真，可以采用电磁散射的方法将海面建模成随机起伏散射面，直接采用数值计算的方法来计算海杂波，但可以预期该方法的运算量较大，在计算量和计算精度之间需折中考虑，这也是天波超视距雷达海杂波仿真的重要思路之一，高精度的目标回波仿真也可以采用这一思路，这也是后续进一步研究的方向.

［1］周万幸.天波超视距雷达发展综述［J］.电子学报，2011，39（6）：1373-1378.ZHOU Wanxing.An overview on development of skywave over-the-horizon radar［J］.Acta Electronica Sinica，2011，39（6）：1373-1378.（in Chinese）

［2］卢 琨.分布式天波超视距雷达体制研究［J］.现代雷达，2011，33（6）：16-19.LU Kun.A study on distributed skywave over-thehorizon radar［J］.Modern Radar，2011，33（6）：16-19.（in Chinese）

［3］CROMBIE D D.Doppler Spectrum of Sea Echo at 13.56Mc.／s［J］.Nature，1955，175（4459）：681-682.

［4］BARRICK D E.Remote Sensing of the Troposphere［R］.Boulder，Colorado：U.S.Department of Commerce，National Oceanic and Atmospheric Administration，University of Colorado，1972.

［5］GILL E W.The Scattering of High Frequency Electromagnetic Radiation from the Ocean Surface-An Analysis Based on a Bistatic Ground Wave Radar Configuration［D］.Newfoundland：Memorial University of Newfoundland，1999.

［6］GILL E W，WALSH J.A combined sea clutter and noise model appropriate to the operation of high-frequency pulsed doppler radar in regions constrained by external noise［J］.Radio Sci，2008，43：RS4012.

［7］GROSDIDIER S，FORGET P，BARBIN Y，et al.HF bistatic ocean Doppler spectra：simulation versus experimentation［J］.IEEE Transactions on Geoscience and Remote Sensing，2014，52（4）：2138-2148.

［8］郭延波.天波超视距雷达探测的海杂波谱模拟研究［D］.新乡：中国电波传播研究所，2007.GUO Yanbo.Research on Spectrum of Sea Clutter Detected by Sky-wave Over-the-Horizon Radar［D］.Xinxiang：China Research Institute of Radio Wave Propagation，2007.（in Chinese）

［9］PALADINI R，MESE E D，BERIZZI F，et al.Fetch limited sea scattering spectral model for HF-OTH skywave radar［C］／／IEEE International Geoscience and Remote Sensing Symposium.July 25-30，Honolulu，2010：4177-4180.

［10］杨龙泉，凡俊梅，蔚 娜，等.天波／地波组合传播模式下一阶海杂波特性分析［J］.电波科学学报，2012，27（4）：703-708.YANG Longquan，FAN Junmei，WEI Na，et al.Study on characteristic of first order sea-clutter in hybrid sky-surface wave propagation mode［J］.Chinese Journal of Radio Science，2012，27（4）：703-708.（in Chinese）

［11］薛永华，柴 勇，刘宁波，等.天波雷达电离层信道建模［J］.电波科学学报，2013，28（5）：862-868.XUE Yonghua，CHAI Yong，LIU Ningbo，et al.Sky-wave OTHR ionospheric channel modeling［J］.Chinese Journal of Radio Science，2013，28（5）：862-868.（in Chinese）

［12］刘春波，陈柏孝，陈多芳，等.岸-舰双基地高频地波雷达一阶海杂波特性分析［J］.电波科学学报，2007，22（4）：599-603.LIU Chunbo，CHEN Baixiao，CHEN Duofang，et al.Characteristic of first-order sea clutter for coast-ship bistatic HF-SWR［J］.Chinese Journal of Radio Science，2007，22（4）：599-603.（in Chinese）

［13］焦培南，张忠治.雷达环境与电波传播特性［M］.北京：电子工业出版社，2007.JIAO Peinan，ZHANG Zhongzhi.Radar Environment and Characteristics of Radio Wave Propagation［M］.Beijing：Publishing House of Electronics Industry，2007.（in Chinese）