太阳闪烁下深空信道建模与电波传播特性分析

吴 桐 闫 毅 李永成 王春梅 姚秀娟 李 雪

（1.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳471003；2.中国科学院空间科学与应用研究中心，北京100190；3.中国科学院大学，北京100049）

引 言

深空探测器受到太阳闪烁的影响会导致通信误码率增高甚至通信中断，进而导致数据传输或测控通信失败.因此，对于有可能飞到太阳背面的探测器，使探测器、太阳、地球近似形成一条直线（即经历太阳“上合”过程）的深空探测任务，需要对太阳闪烁影响下的通信链路的效应进行研究.

从20世纪70年代开始，美国国家航空航天局（National Aeronautics and Space Administration，NASA）在一系列深空探测活动中研究太阳闪烁下的深空通信链路性能，依靠许多探测器聚合时的实验［1-5］，获得了大量观测数据.Feria［6］等人根据遥测数据统计特性并结合太阳探测器轨道的几何模型建立了无线电信号幅度起伏的模型，研究了弱太阳闪烁对通信链路的影响，主要考虑了闪烁指数和信道衰落持续时间，但未考虑时延扩展和频谱扩展.Morabit利用Cassini号的实测数据证实了Feria的统计模型的正确性［7］，又分析了Cassini号获得的频谱扩展和相位闪烁数据，通过对比探测器实测数据、X光观测数据以及理论模型数据，证实了三者的一致性［8］，但也未将频谱扩展等参数引入模型中.国内在这方面研究较为薄弱.由于电离层闪烁与太阳闪烁具有一定的相似性，所以参考电离层信道的建模有助于对太阳闪烁下的深空信道进行建模.Wongtrairat［9］等人建立了平坦电离层闪烁的衰落模型，考虑了幅度统计特性和频谱扩展，但未考虑时延扩展.薛永华［10］等人利用互相关函数建立了电离层信道模型，但其目的是为了雷达探测而不是数据传输，因此，未提出有效的降低误码率的方法.由于时延扩展和频谱扩展对通信系统的影响较为重要，因此，我们建立了同时考虑时延扩展和频谱扩展的太阳闪烁下深空通信信道模型，分析了信道的相干带宽和相干时间，依据日张角的变化提出了深空信号带宽的选择方法.

1 深空通信信道建模

太阳连续发出的太阳风和偶尔发生的日冕物质抛射等太阳事件，均是太阳粒子辐射影响电波传播的因素.这类行星际环境物质处于等离子体态，会使单频电磁波信号产生幅度闪烁、频谱扩展、相位闪烁等现象［4，11］，对有一定带宽的电磁波还产生时延扩展等现象.

一般用闪烁指数来表示幅度闪烁的强弱.闪烁指数可以利用文献［2］中公式（8）进行计算.值得说明的是，虽然闪烁指数是利用弱闪烁近似方法推导得出的，但其在强太阳闪烁情况下依然与观测结果非常符合［12］.再根据闪烁指数与Rician分布中的Rician因子的关系［13］，可以将深空信道电波传播的模型用Rician信道表示.

若设调制后的发送信号为

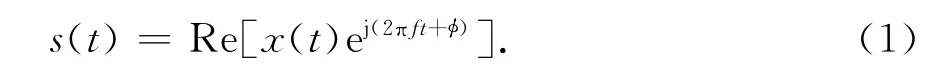
则在有时延扩展和频谱扩展、并考虑加性噪声与干扰的信道中，有视距分量的接收信号的一般表达式为

式中：n（t）为噪声；J（t）为干扰；x（t）为信号复包络；f为载波频率；N（t）表示t时刻时有N（t）条传输路径；αi（t）表示第i条路径t时刻时的幅度衰减系数；τi（t）表示第i条路径t时刻时的延时；φ为载波的初始相位；fDi表示第i条路径中由太阳风随机介质运动引起的频移，与频谱扩展有关.上式中第0条路径为接收信号的视距分量，并且ai（t，fDi）＝

因此，定义信道的闪烁影响因子为

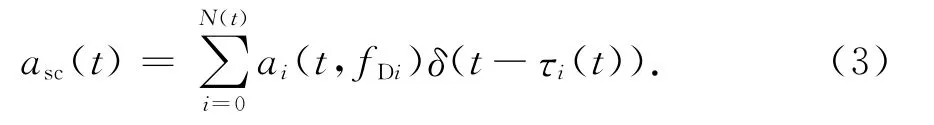
则闪烁影响因子asc（t）的包络R＝｜asc（t）｜的概率密度函数满足Rician分布的概率密度函数，而加性噪声因子n（t）＋J（t）的包络应满足高斯分布.

经过以上分析和推导，太阳闪烁下的深空通信模型可以用图1表示，其表达式为

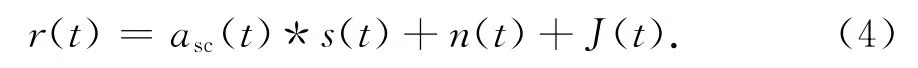
其中，＊表示卷积运算.

实际上，在信道模型中对传输影响较大的两个重要参数是fDi和τi（t），分别对应下文中的相干时间和相干带宽.

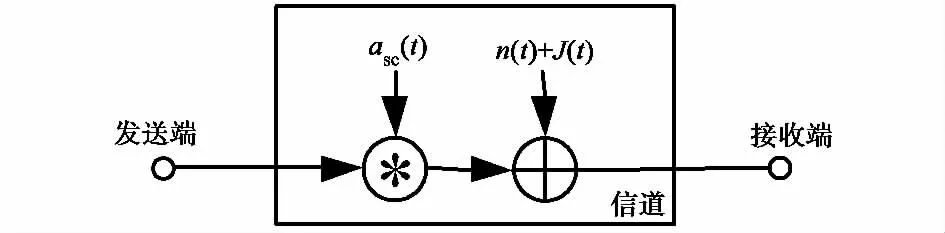
图1 信道模型

2 深空通信信号带宽的确定

2.1 相干时间

随机介质中电波传播的相干时间是利用时变单频电磁波的互相干函数，也即时变单频二阶矩的抛物线方程导出的［3］.相干时间表示两个瞬时时刻信道的冲激响应处于强相关时的最大时间间隔.其物理意义在于，当时间间隔小于相干时间时，信道的特性基本上是相同的.

靠近太阳传播的单频电磁波的频谱扩展为［3］

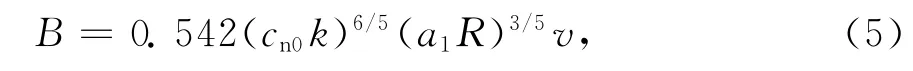
式中：a1＝0.85，为常数；k为电磁波的波数；R如图2所示，表示与太阳中心的距离，图中α为日张角（Solar Elongation Angle）.

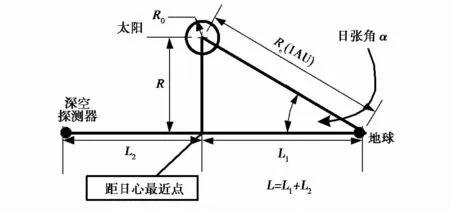
图2 几何模型

传播路径上离太阳中心最近的点（Closest Approach Point）的结构常数cn0的表达式为［3］

式中：σne为传播路径上离太阳中心最近的点的电子密度的均方值，它正比于该点的太阳风电子密度Ne（R）；L0为太阳风湍流结构外尺度.

行星际空间的平均太阳风速度v是与太阳距离的函数，其表达式为［14］

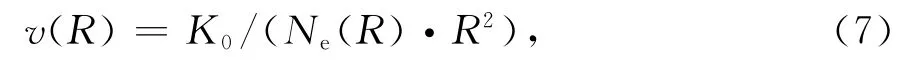
式中，K0为常数，其他参数如前文中定义.太阳风电子密度Ne（R）有很多模型，可根据太阳的周期，从文献［15］提供的模型中选择其一.由于文献［14］未给出K0的取值，这里再给出一种K0的确定方法：从文献［16］中查阅地球附近（R＝1AU处）实时的太阳风速度，代入式（7）便可求得常数K0，从而得到太阳系行星际空间任意点太阳风速度v（R）的精确表达式.

则信道的相干时间约等于频谱扩展B的倒数：

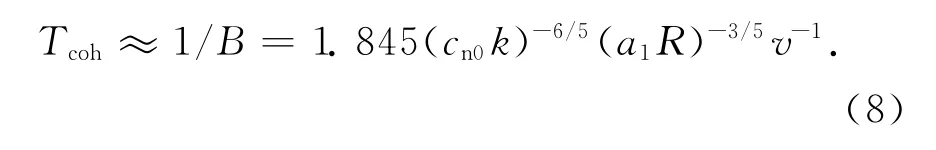
由式（6）和式（8）可以看出行星际介质中传播的电磁波的相干时间随电磁波频率增加而增加，同时也与太阳风速度、太阳风湍流结构的外尺度和电子密度有关.

注意到相干时间随电磁波频率增加而增加，这与陆地移动通信中，相干时间随电磁波频率增加而减小不相同，说明在等离子体中的散射与陆地移动通信中的散射有本质区别.因为在等离子体中，随着电磁波频率的增加，电磁波穿透等离子体的能力也增加，散射效应减弱，从接收端来看，等离子体介质产生的等效散射面减少，从而频谱扩展减小，相干时间增加.电离层中的等离子体与太阳附近行星际的等离子体具有类似的闪烁现象［9，17-18］，但电离层中的等离子体的运动速度较小，大约在0.2km／s的量级［19］，而太阳附近直到地球附近的太阳风，速度达20km／s到500km／s［16］，出现太阳事件时甚至能达到1 000km／s以上.因此太阳附近行星际的等离子体运动引起的时间选择性相对于近地电离层闪烁影响要严重得多.

2.2 相干带宽

随机介质中电波传播的相干带宽是利用非时变双频互相干函数，也即非时变双频二阶矩的抛物线方程推导出的［17，20］.相干带宽表示信道在两个频率处的频率响应保持强相关时的最大频差.其物理意义在于，频率间隔大于相干带宽的两个正弦波受到信道的影响不同.

相干带宽由Xu［17］给出，用来描述电离层的不规则性为

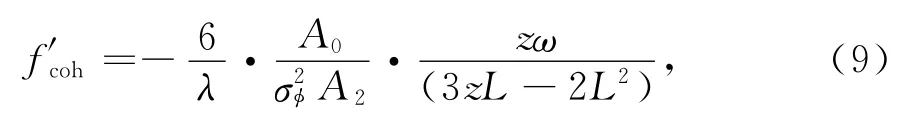
式（9）中参数定义详见文献［17］.

将相干带宽应用于太阳附近的不规则等离子体，则需假设接收端与发射端均处于不规则体内部.可令式（9）中z＝L，则可得太阳附近的不规则等离子体的相干带宽表达式：

式中：ω为电磁波角频率；L如图2所示；电磁波在介质中的波长λ＝2π／k；相位起伏的方差，等离子体波数kp＝ωp／c，等离子体角频率ωp约为

式中：e和m分别为电子的电荷和质量；ε0为真空中介电常数.该角频率表示只有电磁波的角频率ω大于ωp时，电磁波才能在等离子体中传播，否则将引起全反射或强烈衰减.并且，

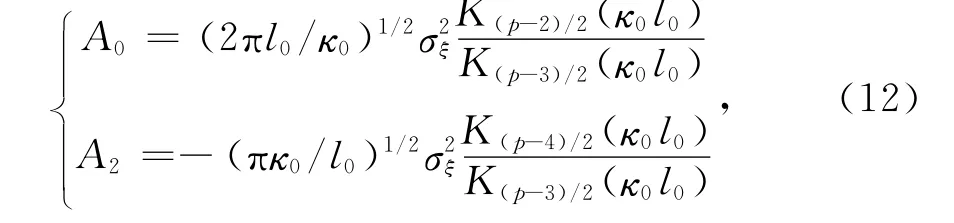
式中：K为虚宗量Hankel函数；l0为太阳风湍流结构内尺度；κ0＝1／L0；电子密度起伏方差＝〈ξ2〉≤1，ξ＝Ne-〈Ne〉／〈Ne〉，p为谱指数，当p＝11／3时，谱为Kolmogorov谱，其他为Shkarosfsky谱.

由式（10）可以看出随机介质中的相关带宽随着电磁波中心频率ω的增大而增大，同时也与太阳风湍流结构的内尺度、外尺度和电子密度有关.

2.3 信号带宽的确定

相干时间和相干带宽决定信道的时间选择性和频率选择性.若设传输信号带宽为W，则若要求深空信道表现出非频率选择性慢衰落特征，W应满足

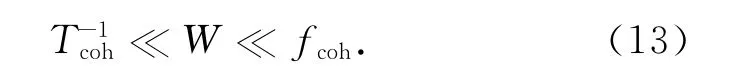
而深空信道的相干时间Tcoh和相干带宽fcoh由式（8）和式（10）确定，再根据图2中的几何关系可知相干时间和相干带宽在其他参数一定时，仅与日张角α有一定的函数关系.

若假设在深空通信中只能使用一种信号带宽，则当日张角由大减小时，选取落在非频率选择性慢衰落区域中最久的带宽作为信号带宽W，误码率性能应为最优的.

按照这样的思路，首先限定Ne（R）、σne、K0、v、f、L0、l0、、L等参数，然后求解关于日张角α的方程为

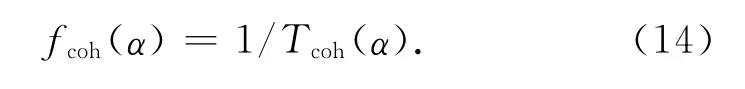
采用数值计算的方法可以解出式（14）确定的日张角αmin，然后代入等式左边或右边得到信号带宽为

则式（15）确定的信号带宽W即为会经历较小日张角的探测器在只能使用一种信号带宽下达到最优误码率的信号带宽.

查阅文献，取太阳风电子密度模型Ne（R）为文献［15］提出的模型，电子密度的均方值σne与Ne（R）的比例 为［12］0.275，地球附近的太阳风速度v（1 AU）为［16］509.8km／s，并根据式（7）求出K0，太阳风湍流结构外尺度为［21］L0＝106km，太阳风湍流结构内尺度为［22］l0＝102km，电子密度起伏方差σξ＝0.5，探测器到传播路径上离太阳中心最近的点L2＝1.2AU，电磁波频率f＝8.4GHz，则将以上参数代入等式（8）、（10）、（14）可求得αmin≈0.3°，再代入式（15）时得到信号带宽W≈40Hz，即在8.4 GHz下当深空探测器的日张角改变时，选取40Hz作为信号带宽可以在日张角α＞0.3°时，均使通信信道呈现出非频率选择性慢衰落，且该日张角为最小值，信道呈现非频率选择性慢衰落的时间最长.

3 模型仿真与信号带宽选择分析

根据国际电信联盟（ITU）对深空地球站的频段划分规定［23］，选取下行的X波段8.4GHz和Ka波段32GHz的两个频率代入式（8）和式（10）进行解析计算，做出信号带宽关于日张角的曲线图，如图3所示，参数选取与2.3节中一致.电磁波中心频率为8.4GHz时（图3中虚线）的相干带宽与相干时间的倒数将平面分为四部分，每一部分代表了一种特性的衰落信道，如图3中黑色框所示.由图3可以看出，非频率选择性慢衰落信道在32GHz时，比8.4 GHz的面积大，因此电磁波中心频率越高则选取的信号带宽落入非频率选择性慢衰落信道的概率也越大.同时，我们可以从图3中得出式（15）确定的信号带宽选择方法的物理意义，即信号带宽为fcoh和曲线交点对应的带宽.

图3 信号带宽与日张角

当电磁波中心频率为8.4GHz时，选取式（15）所对应的频率（约40Hz）作为信号带宽能使得落入非频率选择性慢衰落区域中最久，因此在图4中，我们选40Hz作为信号带宽进行不同日张角下的误码率计算，同时，选取10Hz和400Hz作为对照，信噪比为12dB，调制方式为DBPSK，其他参数与2.3节中一致.由图4可以看出，当日张角α＜0.4°时，选取40Hz的误码率明显好于选取400Hz，这是由于40 Hz的信号带宽进入非频率选择性慢衰落区域更早，虽然400Hz提前进入慢衰落，但其仍处于频率选择性衰落下，码间干扰较大，BER降低不明显；但随着日张角增加，相干带宽迅速增加，码间干扰降低，因此400Hz的BER下降较快，甚至超过了40Hz的BER性能.当0.4°＜α＜1.2°时，40Hz的误码率迅速接近400Hz，并且均好于10Hz的误码率性能.当α＞1.2°时，三种信号带宽的误码率基本一致，为非频率选择性慢衰落信道，并且随着闪烁由强变弱，视距信号逐渐增强，误码率也逐渐降低.

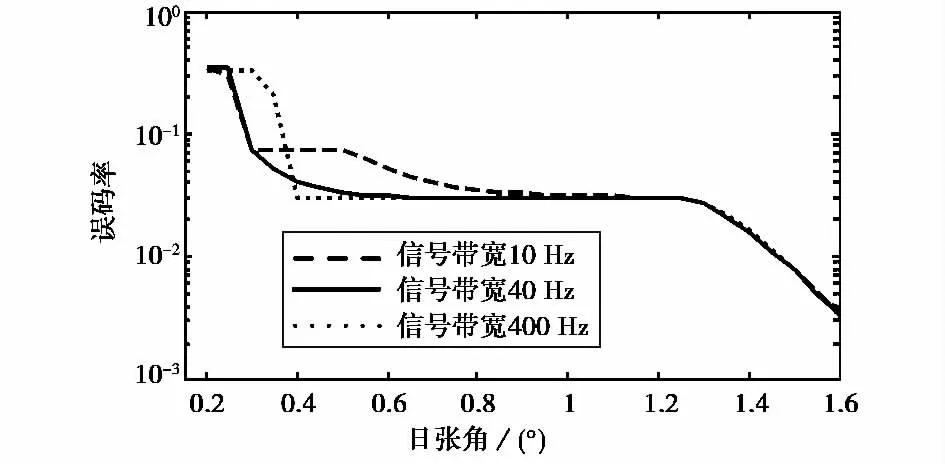
图4 不同日张角与误码率（8.4GHz）

由图5看出，电磁波频率为32GHz时，选取式（15）对应的频率（约40Hz）作为信号带宽在较小日张角范围内的误码率均比10Hz和400Hz好.同样，随着闪烁由强变弱，视距信号逐渐增强，误码率也逐渐降低.调制方式也为DBPSK，信噪比12dB.

从图4和图5综合来看，按照满足式（15）的相干带宽和相干时间来确定信号带宽可以降低通信误码率，从而减小了太阳闪烁带来的影响，提高了通信的可靠性.

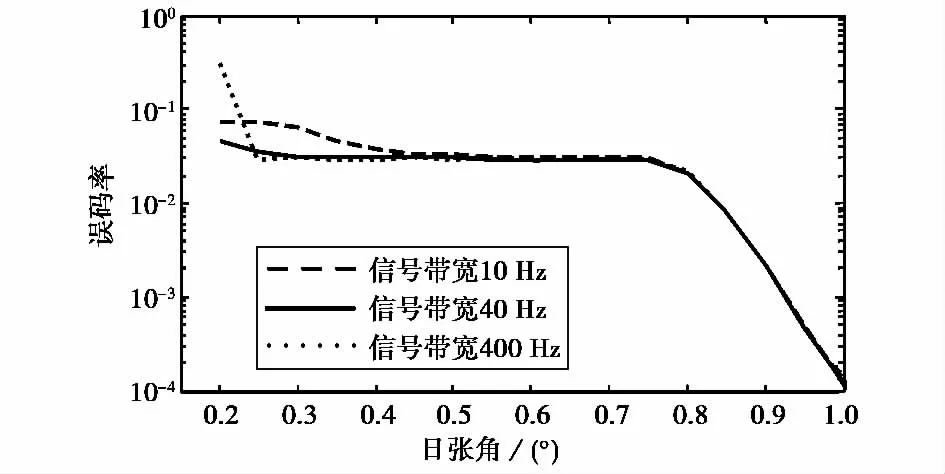
图5 不同日张角与误码率（32GHz）

4 结 论

通过对太阳闪烁影响下的电磁波传播的相干时间和相干带宽的分析，结合Rician衰落信道模型，建立的深空通信信道模型的完整性进一步提高，再利用信道相干时间和相干带宽的计算，确定了深空信道的频率选择性和时间选择性，给出的利用相干时间和相干带宽选择信号带宽的方法，降低了通信误码率，提高了通信的可靠性，为以后开展对太阳或太阳系行星等深空探测活动的测控通信带宽选择技术提供了参考.

［1］BOKULIC R S，MOORE W V.Near Earth Asteroid Rendezvous（NEAR）spacecraft solar conjunction experiment［J］.Journal of Spacecraft and Rockets，1999，36（1）：87-91.

［2］WOO R.Radial dependence of solar wind properties deduced from HELIOS 1／2and Pioneer 10／11radio scattering observations［J］.The Astrophysical Journal，1978，219：727-739.

［3］WOO R，YANG F C，ISHIMARU A.Structure of density fluctuations near the sun deduced from Pioneer-6spectral broadening measurements［J］.The Astrophysical Journal，1976，210：593-602.

［4］MORABITO D D，SHAMBAYATI S，FINLEY S，et al.The Cassini May 2000solar conjunction［J］.IEEE Transactions on Antennas and Propagation，2003，51（2）：201-219.

［5］BOKULIC R S，FLAHERTY M K E，JENSEN J R，et al.The NEAR spacecraft RF telecommunications system［J］.Johns Hopkins APL Technical Digest，1998，19（2）：213.

［6］FERIA Y，BELONGIE M，MCPHEETERS T，et al.Solar scintillation effects on telecommunication links at Ka-band and X-band［J］.The Telecommunications and Data Acquisition Progress Report，1997，129：1-11.

［7］MORABITO D D.Solar corona-induced fluctuations on spacecraft signal amplitude observed during solar superior conjunctions of the Cassini spacecraft［J］.Radio Science，2007，42（3）.doi：10.1029／2005RS003425.

［8］MORABITO D D.Spectral broadening and phase scintillation measurements using interplanetary spacecraft radio links during the peak of solar cycle 23［J］.Radio Science，2009，44（6）.doi：10.1029／2008RS004002.

［9］WONGTRAIRAT W，SUPNITHI P.Statistical modeling of ionospheric scintillation for system modeling［J／OL］.2004［2014-04-06］.http：／／www.kmitl.ac.th／～satcom／publication／paperISEA2004.pdf

［10］薛永华，柴 勇，刘宁波，等.天波雷达电离层信道建模［J］.电波科学学报，2013，28（5）：862-868.XUE Yonghua，CHAI Yong，LIU Ningbo，et al.Sky-wave OTHR ionospheric channel modeling［J］.Chinese Journal of Radio Science，2013，28（5）：862-868.（in Chinese）

［11］HO C M，SUEM K，BEDROSSIAN A，et al.Scintillation effects on radio wave propagation through solar corona［C］／／Proceedings of the XXVIIth URSI General Assembly，Maastricht，URSI，2002.

［12］MORABITO D.Solar Corona Amplitude Scintillation Modeling And Comparison to Measurements at Xband and Ka-band［J］.IPN Progress Report 42-153.Pasadena：Jet Propulsion Laboratory，2003：153.

［13］SHAFT P D.On the relationship between scintillation index and Rician fading［J］.IEEE Transactions on Communications，1974，22（5）：731-732.

［14］BERMAN A L.Solar wind turbulence models evaluated via observations of Doppler RMS phase fluctuation and spectral broadening in the inner corona［J］.The Deep Space Network，1978，44：197-202.

［15］LEBLANC Y，DULK G A，BOUGERET J.Tracing the electron density from the corona to 1AU［J］.Solar Physics，1998（183）：165-180.

［16］空间环境预报中心数据［EB／OL］.SEPC.［2014-06-07］http：／／www.sepc.ac.cn／.

［17］XU Zhengwen，WU Jian，WU Zhensen.Second-order statistics of radio wave propagation through the structured ionosphere［J］.Journal of Atmospheric and Solar-terrestrial Physics，2004，66（11）：971-980.

［18］王国军，史建魁，程征伟，等.海南地区电离层等离子体泡的多仪器同时观测［J］.电波科学学报，2014，29（1）：66-71.WANG Guojun，SHI Jiankui，CHENG Zhengwei，et al.Ionospheric plasma bubbles simultaneously observed by multi-instruments in Hainan region［J］.Chinese Journal of Radio Science，2014，29（1）：66-71.（in Chinese）

［19］蔚 娜，焦培南，杨龙泉，等.运动着的电离层不均匀体的观测研究［J］.电波科学学报，2013，29（2）：372-377.WEI Na，JIAO Peinan，YANG Longquan，et al.Observation research on moving ionospheric irregularities［J］.Chinese Journal of Radio Science，2013，29（2）：372-377.（in Chinese）

［20］YEH K C，LIU C H.An investigation of temporal moments of stochastic waves［J］.Radio Science，1977，12（5）：671-680.

［21］ISHIMARU A.Wave Propagation and Scattering in Random Media［M］.New York：IEEE Press and Oxford University Press，1997.

［22］SPANGLER S R，GWINN C R.Evidence for an inner scale to the density turbulence in the interstellar medium［J］.The Astrophysical Journal，1990，353：L29-L32.

［23］ITU-R.SA.1014-2.Telecommunication Requirements for Manned and Unmanned Deep-space Research［S］.Geneva：ITU，2011.