带电粒子的Mie散射研究

张自嘉 潘 琦 陈海秀

（1.南京信息工程大学信息与控制学院，江苏 南京210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心，江苏 南京210044）

引 言

研究带电粒子对电磁波的散射对云层探测、雷电预警具有重要意义，带电粒子对电磁波的散射能量分布，对分析雷暴云电磁散射信号、以及分析雷暴云的发展具有参考价值.Mie早在1908年就对中性粒子对电磁波的散射给出了描述［1-2］，带电粒子对电磁波的散射，在1977年，由Bohren和Hunt［3］建立了相应的模型并给出了散射系数公式，实际上是对Mie散射的修正，但对具体的带电粒子分析较少，进一步的应用研究不多.近年来，Klacka和Kocifaj对带电粒子对电磁波的散射进行了深入研究［4-7］，计算结果［4-7］和实验［8］均表明了粒子表面电荷会对电磁波散射产生影响.Rosenkrantz和Arnonl研究了纳米带电粒子的电磁波散射，表明粒子带电会增强对电磁波的吸收［9］.Li等还研究了不均匀带电粒子的电磁波散射，表明不均匀带电会引起电磁波散射的变化［10-17］.

已有文献讨论的是散射现象与微观量的关系，散射现象与宏观量的关系研究较少［2-16］，对散射波的整体能量分布较少研究，研究散射波的整体能量分布对雷暴云遥感探测具有重要意义.论文分析了带电球形粒子的散射与宏观量面电导率和电磁阻抗系数的关系，特别是对带电水滴的电磁波散射进行了分析.对电磁波散射系数进行分析和简化，给出了散射系数与面电导率和电磁阻抗系数的关系.表面净电荷形成一种额外的面电导率，通过电导率的变化与外界电场发生相互作用，这种额外的电导率不包括中性粒子中的自由电荷所产生的电导率.

计算了不同面电导率的粒子与中性粒子对电磁波散射系数和散射能量分布，计算表明面电荷使面电导率达到微西门子量级时，就会有明显的影响，随着面电导率的增加，散射系数发生较大变化，但当电导率达到一定值时，散射系数趋于恒定，与粒子的尺度有关.对尺度较大的粒子，带电后的散射系数减小，但沿不同方向的散射能量会重新分配，一些方向散射增强，另一些方向散射减小，尺度较小的粒子带电后，散射系数增大，但能量沿不同方向的重新分配不明显.

1 球形带电粒子的Mie散射系数

如图1所示，考虑一个均匀、各向同性且无磁性的球形粒子（介质1），处于大气或空气（近似为真空）环境中（介质2），球形粒子半径为R，带有净电荷Q，其相对介电系数为ε2＝m2，m为复折射率，空气的相对介电系数为1，真空的介电系数为ε0，环境和粒子的磁导率分别为μ1和μ2，并有μ1＝μ2＝μ0.假设所带净电荷可以在球形粒子表面上自由运动，因此在没有外场用时，会按照静电学的规律，均匀分布在球体的表面，在球体内部没有净电荷分布，设电荷面密度为η.取z轴竖直向上，电磁波的入射方向为k，取xyz坐标系，使k位于xz平面内沿z轴方向.入射电磁波E0沿x轴方向，r为散射波方向.

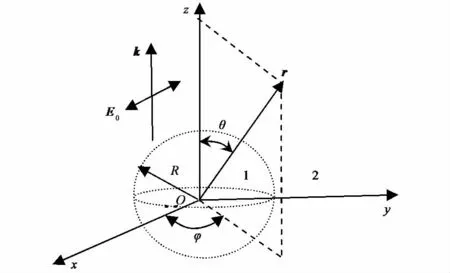
图1 粒子的坐标系选取及入射电磁波

根据文献［1-5］，考虑到

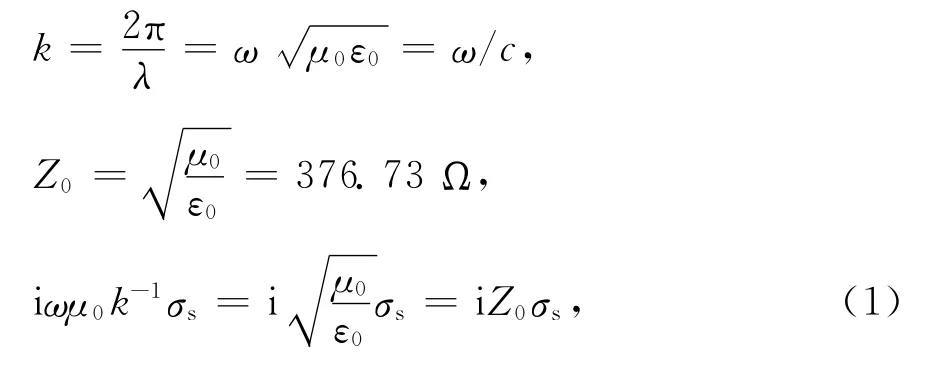
可以将an和bn改为：

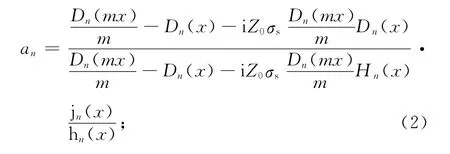
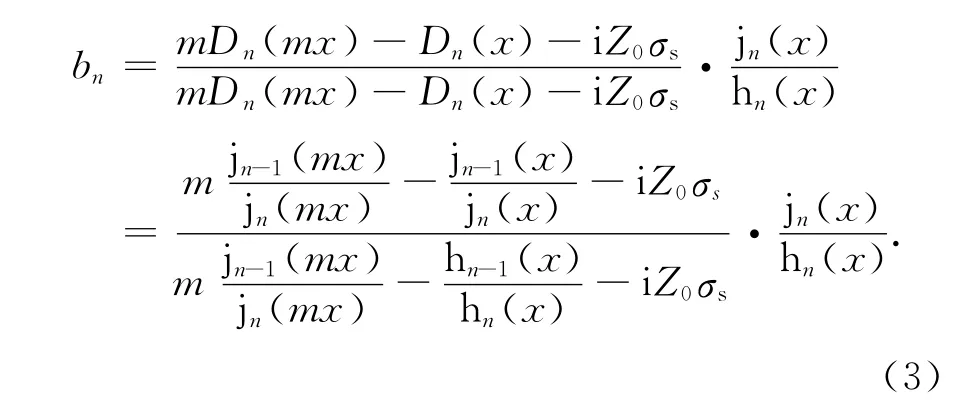
式中：λ为入射电磁波在真空中的波长；ω为角频率；c为真空中的光速；σs为球形带电粒子的表面电导率；

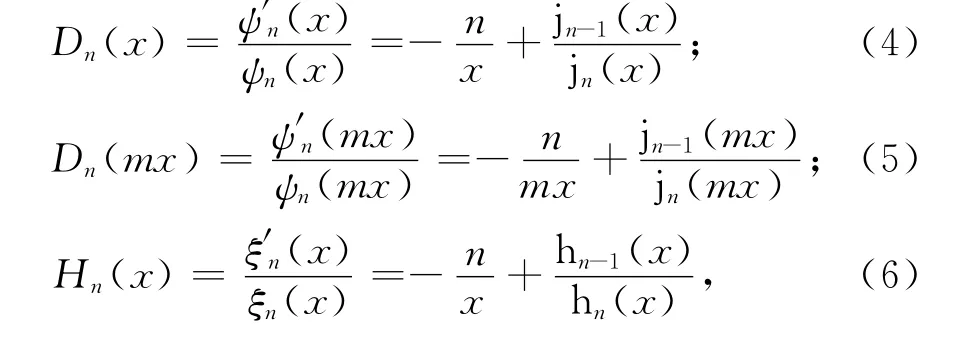
ψn（ρ）＝ρjn（ρ），ξn（ρ）＝ρjn（ρ），jn（ρ）为第1类球贝塞尔函数，hn（ρ）为第1类球汉克尔函数，（ρ）＝dψn（ρ）／dρ，ξ′n（ρ）＝dξn（ρ）／dρ.取μ1＝μ0，x＝kR＝2πR／λ，在an和bn的表达式中等式，在一般的x范围内，如0.1～100，其绝对值在100以下，因此Z0σs如果也和它们在同一量级，就会产生明显的影响，而Z0＝376.73Ω，为电磁阻抗系数，因此面电导率σs在微西门子量级时就会产生影响.x越大，这一比值越小，Z0σs的影响越大.

用Qsca、Qext和Qabs分别表示散射系数、吸收系数和消光系数，则有［1-2］：

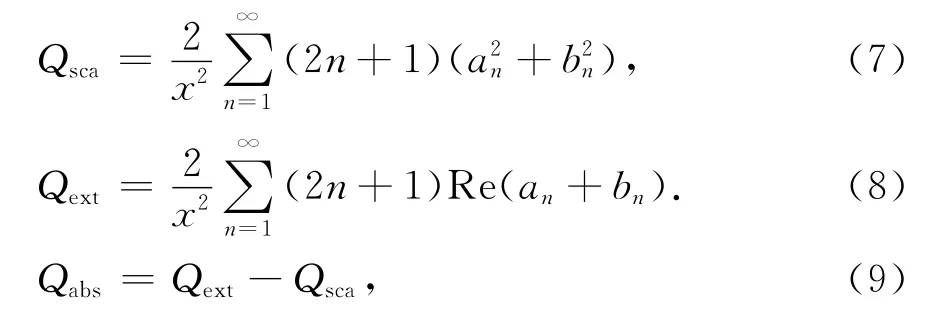
2 面电导率分析

文献［5］对面电导率进行了较为详细的分析，这里从另外一个角度对面电导率进行分析.电导率与可移动电荷的密度有关，即电子的密度有关，当粒子带上电荷后会产生额外的面电导率，一般意义上的电导率与运动电荷密度有关，面电导率与表面上可运动的面电荷密度有关，但在式（1）中，面电导率只与净电荷引起的电导率有关，而与不带电时的电荷密度无关.

对两介质的分界面，电荷守恒定律得到的电流边值关系为

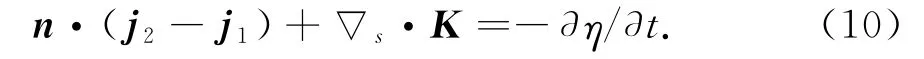
式中：n为由介质1指向介质2的法向矢量；j1和j2分别为介质1和2中的电流密度；K为面电流密度；η为表面电荷密度.

设球形粒子带电量为q，电势为u，则q＝4πε0uR，于是η＝q／4πR2＝ε0u／R.实际上电荷是分布在表面的一个薄层内，如图2、3所示，粒子上的电荷由于受到约束聚集于粒子的表面，表面电荷处于自身所携带电荷的电场中，可以计算出这一电场的大小为

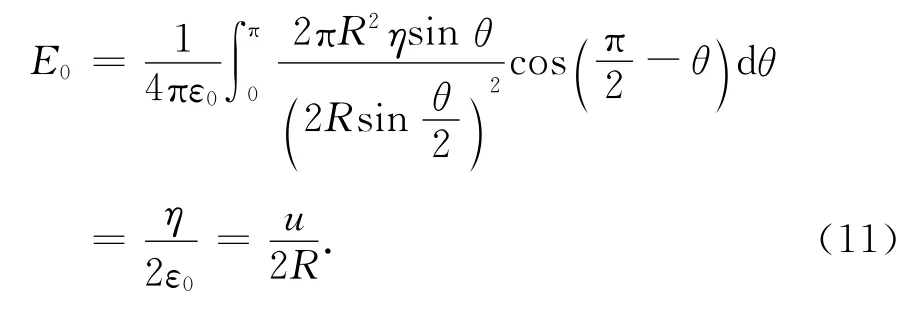
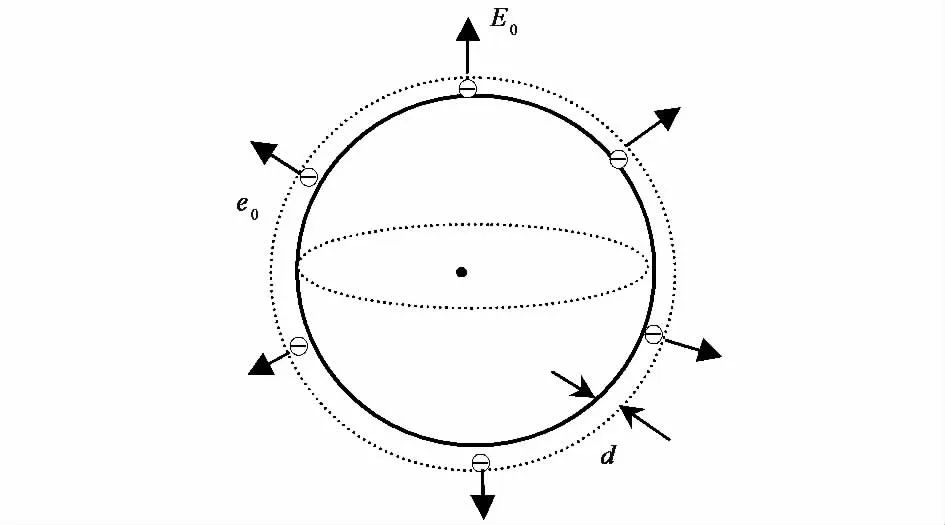
图2 带电球形粒子的表面电荷

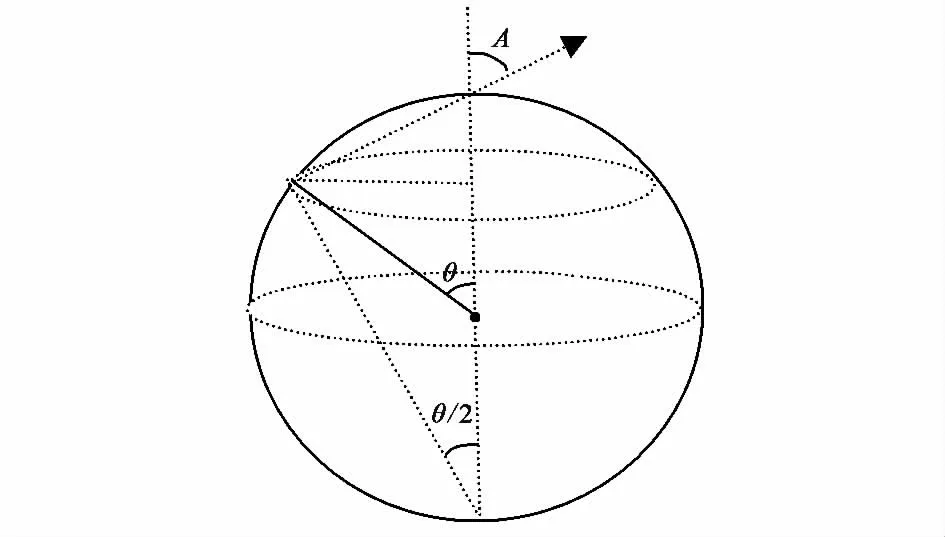
图3 表面电荷之间的相互作用

在没有入射电磁波的情况下，表面电荷受到径向电场E0的作用，在表面约束的共同作用下处于平衡状态，对半径R较小的粒子，E0有较大的值，如R＝10μm，u＝10V，E0＝5×106V／m，只有很强的电磁波才能达到这样量级的电场强度，因此强度较小的入射波不会引起电子的径向运动，电荷仍在粒子的表面运动，不会进入粒子的内部.此外电磁波入射到介质表面特别是导体表面的穿透深度为z0＝对可见光入射到通常的良导体表面，这一值约为nm量级.

设薄层的厚度为d，则薄层内电荷的体密度为ρ＝η／d＝ε0u／Rd，若所带电荷为电子，电子的电量为e0，则粒子表面电子的数密度为N＝η／de0＝ε0u／Rde0，可见d越小，数密度越大.而面电导率与数密度N成正比，N越大面导电率就越大.

对电磁波，时间因子写为e-iωt，则，其中略去因子e-iωt，在研究粒子对电磁波散射时，没有电流从两介质交界面上流过，也没有内部电荷向交界面上聚集，这与中性粒子类似，中性粒子对电磁波的散射，也不涉及电荷向交界面的聚集，则n·（j2-j1）＝0，于是

面电流密度与自由面电荷密度有关，面电荷密度是面电流的源，这里的面电荷密度只与所携带的净电荷有关，不涉及中性状态时的自由电荷密度.面电荷受到外界电场的作用引起电流，面电荷的存在实际上是改变了原来的面电导率，根据欧姆定律K＝σsE，对中性导体，电导率与电子密度成正比，结合式（12），K与η有关，则面电导率σs是由所携带面电荷引起的，若没有面电荷，则不会存在面电流K，σs不包括中性粒子中的电子密度.

3 球形带电粒子的Mie散射系数计算

Qsca、Qext和Qabs的计算，需要计算an和bn，已有不少文献分析了an和bn的计算方法［18-25］，实际上不少算法形成于20世纪六七十年代.由于当时计算机性能不强，容易溢出，但随着计算机的发展，在非极端情况下，对通常的粒子如云雾、雨滴等，x和m不是很大时，可以较容易计算，不会出现溢出，当x较大时散射系数趋于恒定.

图4给出了金属球形铜粒子带电前后散射系数的变化，其中取铜的折射率m＝0.62＋2.57i.由于铜本身的良导电性，可以看出带电后散射系数有变化，但变化不很大，图中σs的单位均为西门子S.

图5给出了球形水滴在不同面电导率时Qsca、Qext和Qabs与x的关系曲线.

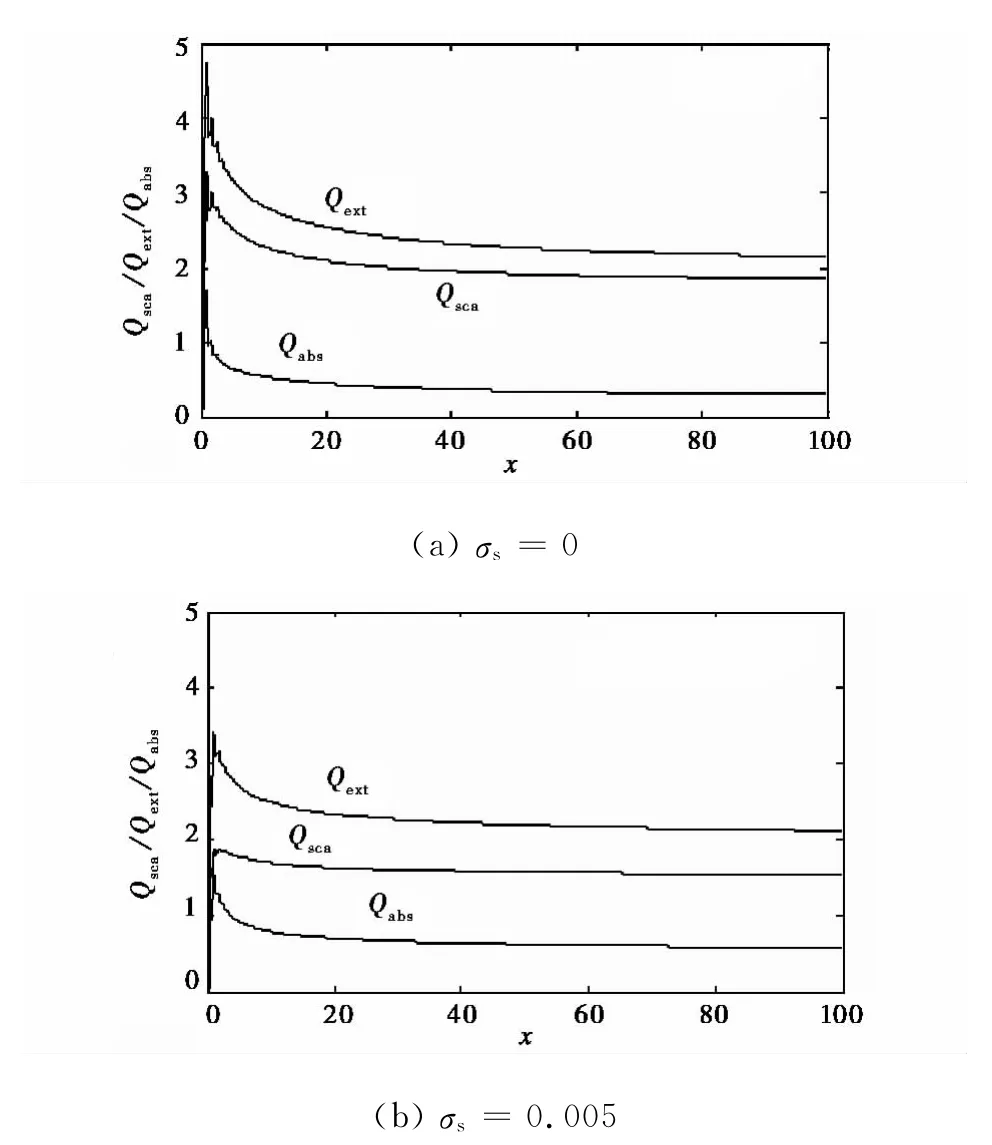
图4 带电球形金属（Cu）粒子在不同面电导率时Qsca、Qext和Qabs与x的关系

从图5可以看出，对球形水滴粒子，随着σs的增加，Qsca和Qext整体在减少，Qsca随着x变化时的波动变小，其散射特点趋向于同金属粒子的散射特点.随着参数x的增大，伴随着明显的振荡现象，x越小这种振荡越明显.这种振荡是由电多极子和磁多极子耦合产生的［26］.x不同时电多极子和磁多极子具有不同的振荡形式和强度，波长一定而粒子直径增大时，电多极子和磁多极子的振荡加强，两者的叠加便出现了强烈振荡现象.而当面电导率增加时，趋近于具有金属的特性，电多极子与磁多极子的耦合减弱，振荡幅度减小并消失.

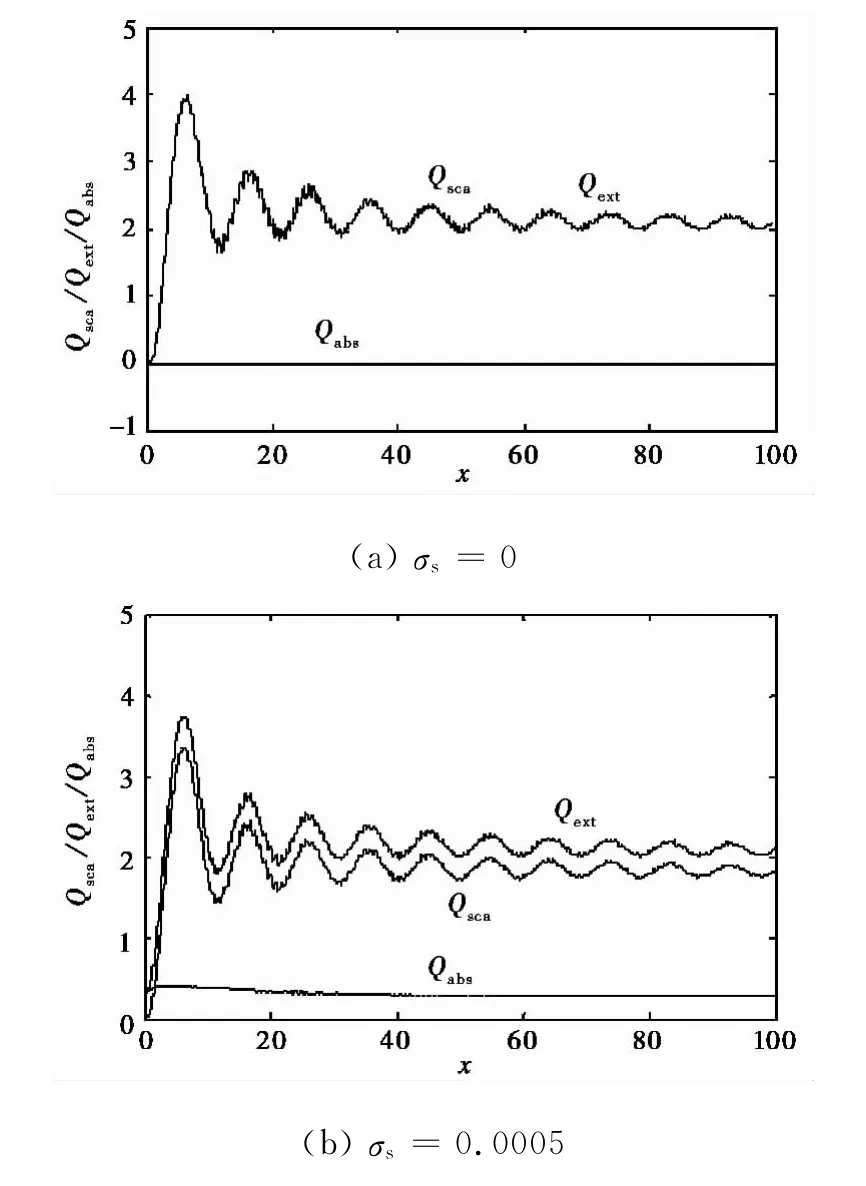
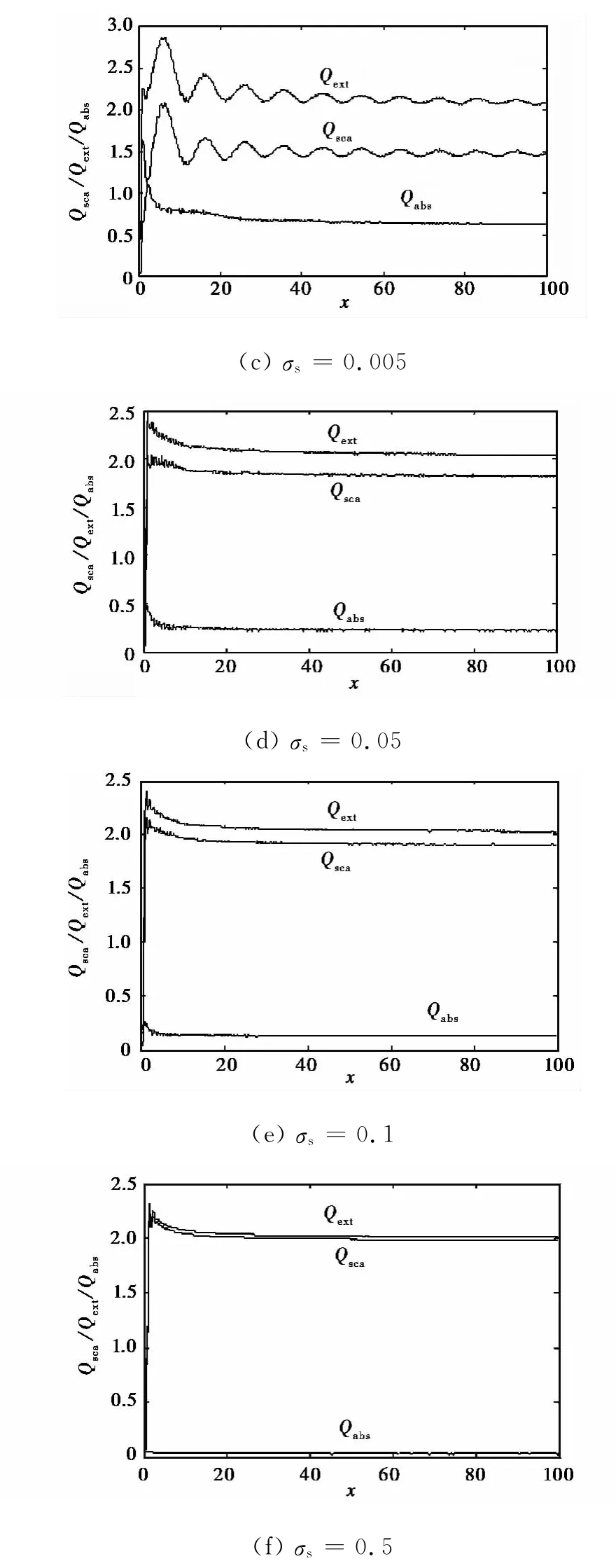
图5 带电球形水滴在不同面电导率时，Qsca、Qext和Qabs与x的关系

图6给出了x值一定时，Qsca、Qext和Qabs随电导率的变化，可见x一定且较小时，随着σs增加，Qsca先增加后减小.因为不带电时，中性粒子的散射系数较小，因此当σs较小时，Qsca有一个增加过程，但Qsca的值较小.当x较大时，中性粒子的散射较强，随着σs增加，Qsca反而会减小.

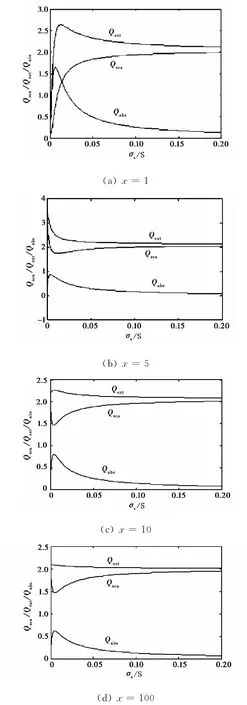
图6 带电球形水滴Qsca、Qext和Qabs与σs关系

4 球形带电粒子的散射光强与散射角的关系

在对散射进行观测时，需要掌握沿某一方向的散射强度，散射波的振幅为［1-3］

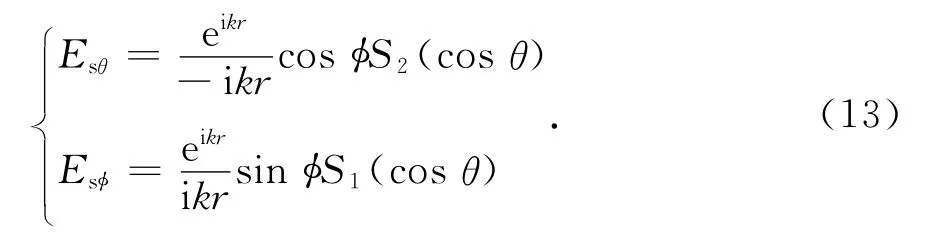
式中：

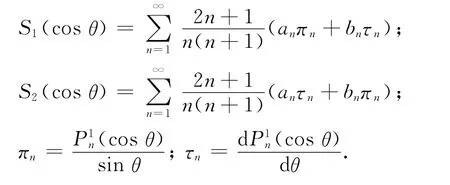
计算时需要根据对应的递推关系，由于光强与振幅的平方成正比，因此需要计算｜S1（θ）｜2和｜S2（θ）｜2，由于变化幅度比较大，因此给出的结果为lg（｜S1（θ）｜2）～θ和lg（｜S2（θ）｜2）～θ，取不同的σs进行计算.图7给出x＝10，σs＝0，0.000 5，0.005，0.05时，lg（｜S1（θ）｜2）～θ和lg（｜S2（θ）｜2）～θ，左边为｜S1｜2，右边为｜S2｜2.

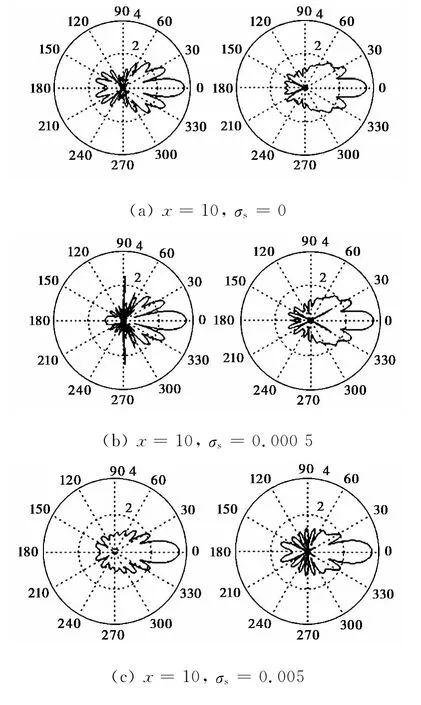
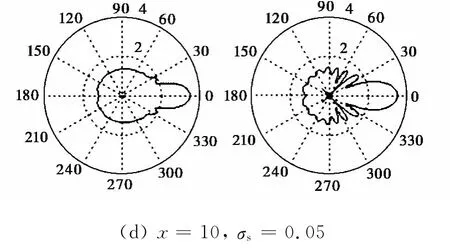
图7 带电球形水滴x＝10，σs＝0，0.000 5，0.005，0.05S时｜S1｜2和｜S2｜2与角度的关系

图8给出了x＝30，σs＝0，0.05时，lg（｜S1（θ）｜2）～θ和lg（｜S2（θ）｜2）～θ，可以看出，随着σs增加，｜S1｜2和｜S2｜2沿不同角度的值发生了变化，边瓣减弱.图8（a）、8（b）、8（c）、8（d）中左边为｜S1｜2，右边为｜S2｜2.散射波的强度分布呈现多瓣结构，是由于散射波的干涉形成的，x较小即波长与粒子直径接近时，前向散射强，与通常的散射规律相同.电导率增加时散射的多瓣结构减弱，趋于更均匀，但前向散射仍较强.

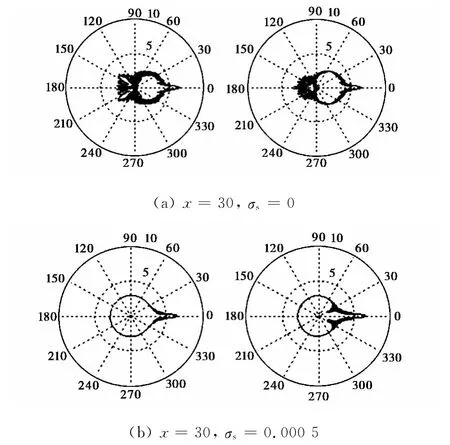
图8 带电球形水滴x＝30，σs＝0，0.05S时｜S1｜2和｜S2｜2与角度的关系

实际观测时，需要观测侧向或后向散射，可以证明，对后向散射，有

图9给出了x＝1和x＝10时，后向散射的｜S1｜2和｜S2｜2随σs的变化曲线（｜S1｜2＝｜S2｜2）.

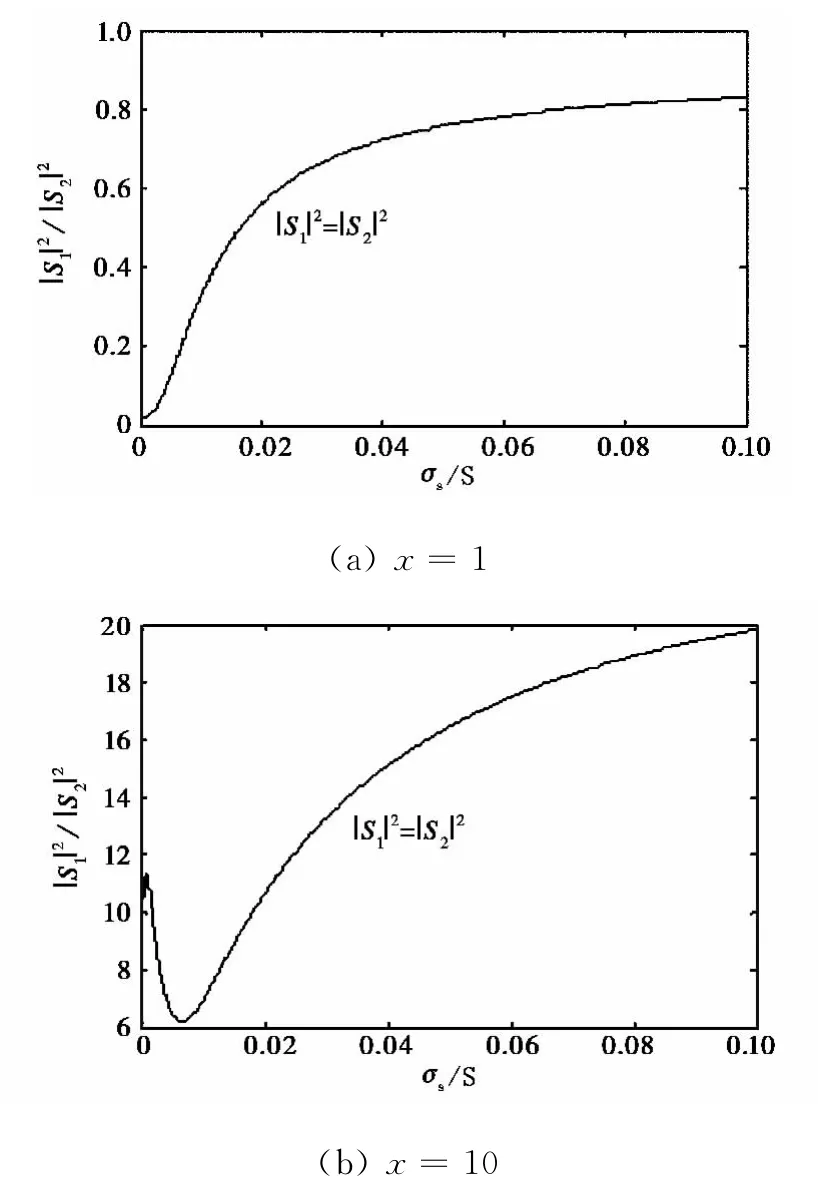
图9 带电球形水滴的后向散射｜S1｜2＝｜S2｜2与σs的关系

从图9可以看出，后向散射系数会随σs的增加而增加，在x较大时，后向散射系数与σs不是单调关系.随着σs的变化，散射的能量沿不同方向重新分配，有些方向增加，而另外的方向则会减小.

5 总结与讨论

研究了带电粒子对电磁波的散射特点，给出了散射系数与电磁阻抗系数及表面电导率的关系，计算了不同面电导率的粒子与中性粒子对电磁波散射系数和散射能量分布的差别，计算表明：对金属类粒子，带电后的散射影响不大；但对带电后导电的介质类粒子如水粒子，面电荷使面电导率达到微西门子量级时，就会有明显的影响.

随着面电导率的增加，散射系数发生较大变化，但当电导率达到一定值时，散射系数趋于恒定.相对中性粒子的散射，z较大的粒子，带电后的散射整体会使散射系数减小，但沿不同方向的散射能量会重新分配，后向、侧向和前向有不同的特点，与粒子的尺度x有关，有些随着电导率的增加散射系数会增加，有些先减小然后增加，而尺度较小的粒子带电后沿不同方向的散射能量变化不大.

［1］HULST H C.Light Scattering by Small Particles［M］.New York：Dover Publications Inc，1983：114-161.

［2］BOHREN C F，HUFFMAN D R，Absorption and Scattering of Light by Small Particles［M］.New York：John Wiley ＆Sons，1983：83-175.

［3］BOHREN C F，HUNT A J.Scattering of electromagnetic waves by a charged sphere［J］.Can J Phys，1997，55：1930-1934.

［4］KLACKA J，KOCIFAJ M.Scattering of electromagnetic waves by charged spheres and some physical consequences［J］.Journal of Quantitative Spectroscopy ＆Radiative Transfer，2007，106：170-183.

［5］KLACKA J.On the scattering of electromagnetic waves by a charged sphere［J］.Progress in Electromagnetics Research，2010，109：17-35.

［6］KOCIFAJ M，Klacka J.Scattering of electromagnetic waves by charged spheres：near-field external intensity distribution［J］.Optics Letters，2012，37（2）：265-267.

［7］KOCIFAJ M，KLACKA J.Scattering of electromagnetic waves by charged spheres：near-field external intensity distribution［J］.Optics Letters，2012，7（2）：265-267.

［8］HEIFETZ A，CHIEN H T，LIAO S，et al.Millimeter-wave scattering from neutral and charged water droplets［J］.Journal of Quantitative Spectroscopy ＆Radiative Transfer，2010，111：2550-2557.

［9］ROSENKRANTZ E，ARNON S.Enhanced absorption of light by charged nanoparticles［J］.Optics Letters，2010，35（8）：1178-1180.

［10］LI X，LI X C，ZHENG X J，et al.Attenuation of an electromagnetic wave by charged dust particles in a sandstorm［J］.Appl Opt，2010，49（35）：6756-6761.

［11］ZHANG B，LI X.Electromagnetic scattering by a partially charged multilayered sphere［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，2014，148：228-232.

［12］LI X C，ZHANG B.The electromagnetic scattering of the charged inhomogeneous sand particle［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，2013，119：150-154.

［13］LI X C，MIN X，LIU D D.Rayleigh approximation for the scattering of small partially charged sand particles［J］.JOSA，2014，31（7）：1495-1501.

［14］LI X C，LI X，ZHENG X J.Comparison between the Mie theory and the Rayleigh approximation to calcu-late the EM scattering by partially charged sand［J］.Journal of Quantitative Spectroscopy ＆Radiative Transfer，2012，113：251-258.

［15］何琴淑，周又和，郑晓静.带电沙粒的散射场及其对电磁波传播的影响［J］.中国科学G辑，2005，35（3）：308-317.HE Shuqin，ZHOU Youhe，ZHENG Xiaojing.Scattering electromagnetic field of charged sands and the effects on the tranmission of electromagnetic wave［J］.Science in China Series G，2005，35（3）：308-317.（in Chinese）

［16］张自嘉，王 其，孙亚杰，等.大气带电粒子对电磁波的散射［J］.电波科学学报，2011，26（4）：758-764.ZHANG Zijia，WANG Qi，SUN Yajie，et al.Scattering of electromagnetic waves by charged particles in atmosphere［J］.Chinese Journal of Radio Science，2011，26（4）：758-764.（in Chinese）

［17］何琴淑，周又和.带电椭球粒子对电磁波的散射［J］.兰州大学学报：自然科学版，2004，40（2）：25-30.HE Qinshu，ZHOU Youhe.Scattering of electromagnetic wave by charged spherical particle［J］.Journal of Lanzhou University：Natural Sciences，2004，40（2）：25-30.（In Chinese）

［18］赵振维，吴振森，薛谦忠.大尺寸均匀有耗球电磁散射的算法［J］.电波科学学报，1999，14（4）：422-455 ZHAO Zhenwei，WU Zhensen，XUE Qianzhong.An algorithm for electromagnetic scattering of large absorptive homogeneous sphere［J］.Chinese Journal of Radio Science，1999，14（4）：422-455.（in Chinese）

［19］丁大志，沈 鹏，陈如山.降雨粒子群散射特性的高效分析［J］.电波科学学报，2012，27（1）：30-37.DING Dazhi，SHEN Peng，CHEN Rushan.Electromagnetic scattering of precipitation particle group［J］.Chinese Journal of Radio Science，2012，27（1）：30-37.（in Chinese）

［20］LENTZ W J.Generating Bessel functions in Mie scattering calculations using continued fractions［J］.Appl Opt，1976，15（3）：668-671.

［21］WISCOMBE W J.Improved Mie scattering algorithms［J］.Appl Opt，1980，19：1505-1509.

［22］HONG D.Mie-scattering calculation［J］.Appl Opt，2004，43（9）：1951-1956.

［23］CACHORRO V E，SALCEDO L L.New improvements for Mie scattering calculations［J］.J Electromagn Waves，1991，5（9）：913-926.

［24］YANG W.Improved recursive algorithm for light scattering by a multilayered sphere［J］.Appl Opt，2003，42（9）：1710-1720.

［26］PLUCHINO A B.Infrared emissivity of single water droplets［J］.Appl Opt，1979，18（24）：4065-4066.