基于阵元相位调控的天线罩瞄准误差快速优化

王 威 万国宾 王 丽 沈 静，2

（1.西北工业大学电子信息学院，陕西 西安710129；2.航空电子系统射频综合仿真重点实验室，江苏 无锡214063）

引 言

天线罩是现代飞行器电子系统不可或缺的组成部分.电磁波通过天线罩时会产生波前畸变，致使天线指向的目标角位置偏离实际位置，这个偏角被称为瞄准误差［1］.因为关系到雷达的跟踪精度，在天线罩的设计、生产、使用阶段，都有相应的策略抑制瞄准误差.在使用阶段（特别针对导弹天线罩），常用的方法是结合存储的瞄准误差测量结果，用软件方式通过飞行控制回路进行补偿.在生产阶段，可以采用局部罩壁修磨技术，通过修磨槽的尺寸和分布控制瞄准误差［2］.而最基本的方法，还是在设计阶段，借助合理的优化设计让瞄准误差消于无形.从早期的准对称相位法［1］，到Hsu首先使用并得到广泛响应的基于进化算法的优化方法［3-4］，瞄准误差优化的目标大多在于找到最合理的罩壁厚度分布，减少罩壁对天线指向的影响.同时也有另一种思路［5］，将带罩相控阵天线看作一个整体，调节天线的辐射特性，同样能达到抑制瞄准误差的功用，它可以作为罩壁优化方法的有益补充.

当前多数相控阵天线都通过二进制数字移相器控制其辐射的指向.由于相位量化误差的存在，移相器的精度直接受制于它的位数，而较高位数的移相器往往意味着复杂的结构与高昂的成本，所以需要在有限位数条件下尽力减小量化误差.较早提出用于提高量化精度的移位加权馈相法［6］，不适于加罩天线的设计.而近年得到较多关注的随机馈相法［7］，更适用于阵元数目达到一定规模的情况.面对低成本市场需求，Ciattaglia提出一种相位偏移优选技术［8］，能有效提高基于低位移相器的小型阵列指向精度，但其计算效率尚有一定提升空间.

此外，在天线罩优化中常用的进化算法需要计算大量样本所对应的辐射特性.因此，对于样本适应度函数计算，任何效率方面的提升均是有意义并且必要的.

本文将以低位数字移相器的状态调节为手段，建立一种天线罩瞄准误差优化设计的快速方法.文中首先分析激励优化瞄准误差问题的计算模型及其连续粒子群优化（Particle Swarm Optimization，PSO）算法实现，在此基础上建立基于相位偏移优选技术的带罩天线性能离散PSO优化方法；然后提出一种基于先验信息的瞄准误差高效优化方法，改进连续与离散PSO速度更新公式；之后通过分析带罩天线辐射公式，建立用于计算辐射场的位置关系矩阵，提高优化效率.最后给出了瞄准误差优化验证算例.

1 分析方法

1.1 瞄准误差修正原理

如果将天线罩的材料与结构等参数表示为Xr，将天线阵列的激励参数表示为Xa，带罩天线的某一种性能参数可以表示为

式中，Θ＝［θmin，θmax］与Λ＝［fmin，fmax］分别代表天线指向θ与工作频率f的集合.在天线罩本身参数Xr已经优化确定的前提下，为进一步提高带罩天线系统的性能，便可对Xa进行优化操作.参考文献［9］对天线罩厚度优化问题的定义，带罩阵列激励优化问题可以归纳为如下形式

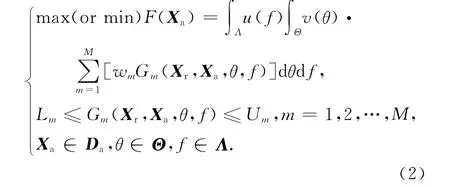
式中：u（f）与v（θ）为体现不同频带与扫描角下电性能参数要求的权函数；wm为各个电性能参数的权因子；Da为激励矢量Xa的取值空间；Lm与Um表示性能参数Gm的允许取值上下限.

为了实现以瞄准误差优化为主，兼顾透波率优化的目标，选择调节天线阵激励相位，使所需天线罩系统参数达到最佳.根据数值计算需要，可将θ限制在若干离散点上.对于单一频率优化问题，可以忽略其影响.于是优化问题可表示为

式中：B（Xa，θ）代表天线罩的瞄准误差；P（Xa，θ）代表透波率；代表第n阵列单元的相位；表示φn的基准值；ε表示φn的可调节范围.若阵元间隔为d，波长为λ可由下式确定

通过为式（3）中的权重因子w1与w2选择合适的值，即可实现瞄准误差为首要控制参数的期望.

1.2 瞄准误差修正实现过程

PSO方法的每次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，即

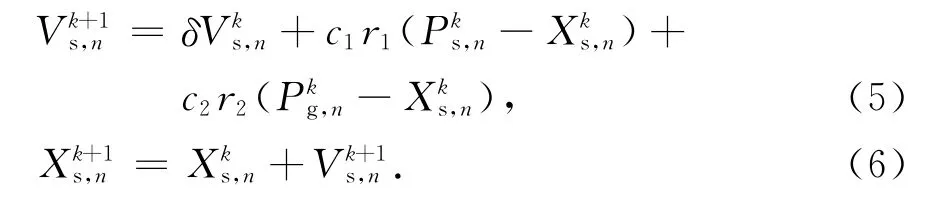
式中：Vs，n为粒子速度；Xs，n为粒子位置；Ps，n为个体极值；Pg，n为群体极值；δ为惯性权重；k为当前迭代次数；c1和c2是加速度因子；r1和r2是分布于［0，1］区间的随机数.瞄准误差优化中用于评价粒子的适应度函数为

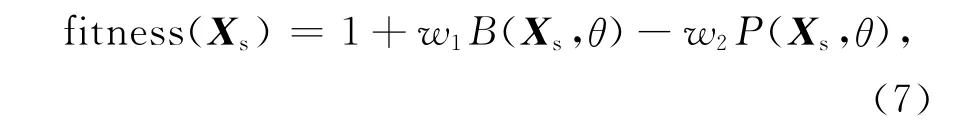
粒子Xs表示相位调节量ξ＝φ-φ0.

公式（5）、（6）基于相位连续可调的假设，而实际优化中相位通常由移相器控制，只能是最小调节量φs的整数倍，所以有必要建立针对数字相位的优化方法.我们在相位数字优化过程中采用一种相移优选技术［8］.对各个阵元相位基准值加入等量的相移K，K的加入并不改变理论天线指向，但会影响数字化后的移相器状态值由下式得到

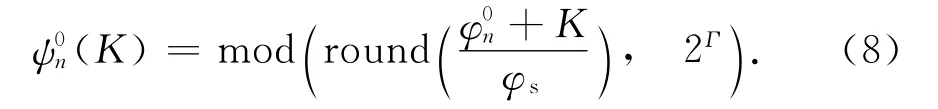
式中：round表示取整运算；mod表示求余运算；Γ为移相器位数.通过选择合适的K，可以用较低位数移相器取得符合要求的相位数字化效果.

数字相位优化依然采用式（3）定义的优化过程，但矢量Xa包括了相移K与数字相位ψ，即

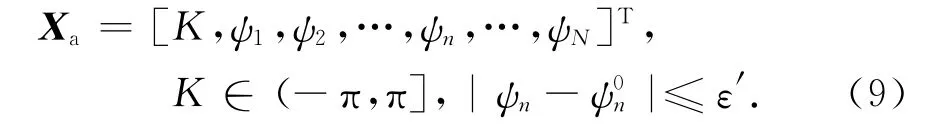
式中，可调范围ε′是一个有限的整数，因为ψn只能在有限的临近状态位置上跳变.

对于Γ位移相器，阵元相位状态ψ可以由一个Γ×N长度的位数序列表示，例如当Γ为4时，有

b为0或1.如果相位状态ψ在优化中作2位偏移，而K作10位离散，那么粒子Xs可表示为

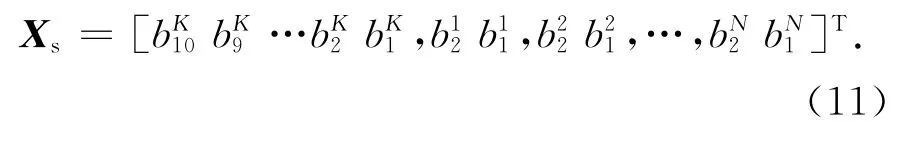
离散PSO的粒子更新公式为：

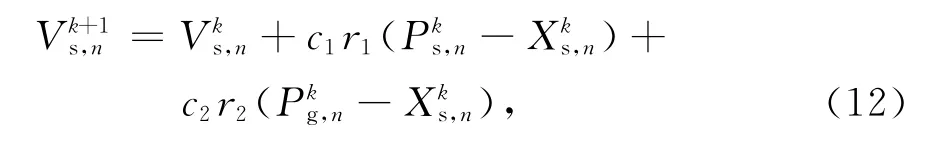
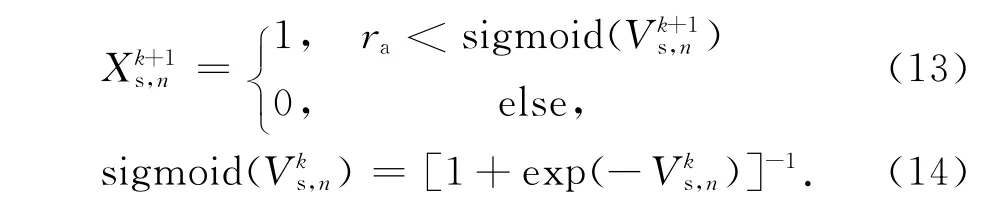
1.3 基于先验信息的高效优化

若Δ（θ）表示天线罩对天线指向θ造成的偏转角.对期望指向θ的带罩天线系统而言，当天线指向角为θ-Δ（θ）时，系统瞄准误差接近于0.所以使天线指向θ-Δ（θ）的相移ξe接近于优化的最终解，并有

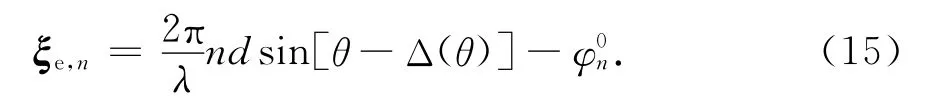
为了在PSO优化中更高效准确地得到最优解，可以利用ξe这一已知信息改良现有迭代公式.对于连续PSO，可建立近似解Pe＝ξe，修改式（5）中的速度公式为

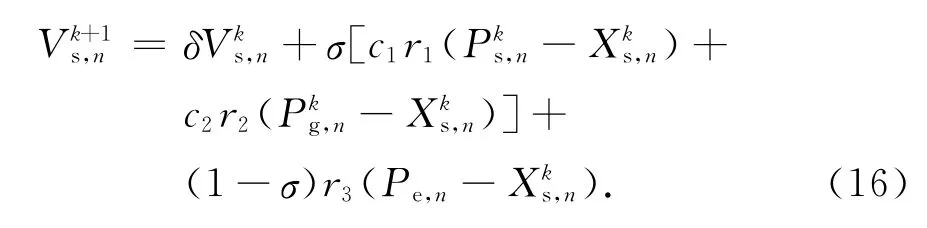
在改进迭代公式（16）中，粒子的位置更新不再仅仅依靠跟踪个体极值Ps与群体极值Pg，而且会参考近似解Pe的位置.Ps、Pg与Pe的影响力由权重系数控制.在迭代初期，σ的值较小，将促进粒子快速向近似解附近区域移动，因为这也是精确解所在的区域；之后，σ的值会迅速变大，并趋于1，表明近似解对算法的干扰作用受到了抑制，有利于精确实现局部搜索.

对于离散PSO，近似解Pe由最优相移Ke与最佳移相器状态ψe编码得到.Ke与ψe应使天线指向最接近θ-Δ（θ），它们的值可以通过在K的定义区间内采样计算后寻优获得.

1.4 数值算法效率提升

如图1所示的二维天线—罩系统，相控阵天线呈一组平行于z轴的无限长线电流激励源Ⅰn（n＝1，2，…，N），阵元间隔为d.天线罩长为L，底部直径为D.罩内表面第p（p＝1，2，…，P）个剖分单元处的入射电磁场为：

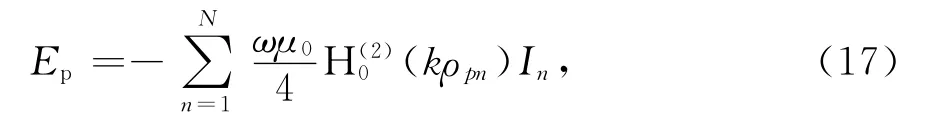
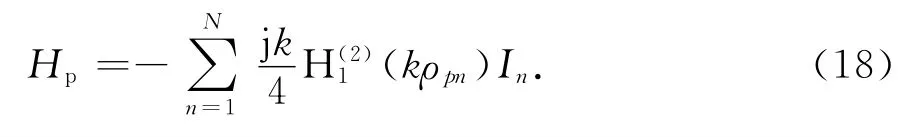
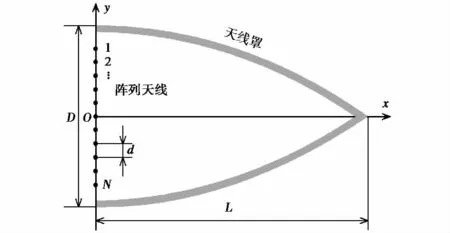
图1 带罩阵列天线示意图

式中：ω是电磁波角频率；k是自由空间波数；μ0是自由空间导磁率；ρpn为源点与场点的距离；分别为第二类和第一类零阶汉克尔函数.通过传输线矩阵法，可以由罩内表面入射电磁场求得罩外表面上的等效电流J与等效磁流M，具体过程见文献［9］.等效电磁流在远场点q处的辐射电场用数值积分可以表示为

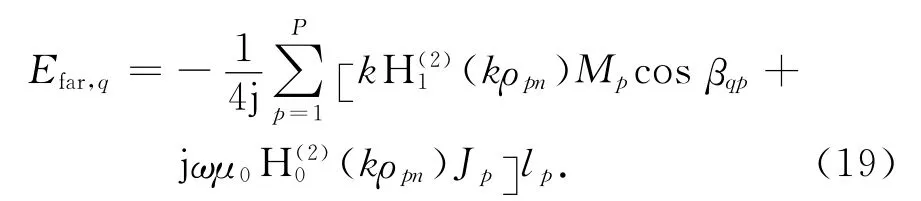
式中：lp为罩外表面剖分区间长度；βqp为辐射方向与外表面法向矢量的夹角.

如果设

那么式（17）至（19）可以表示为如下形式：

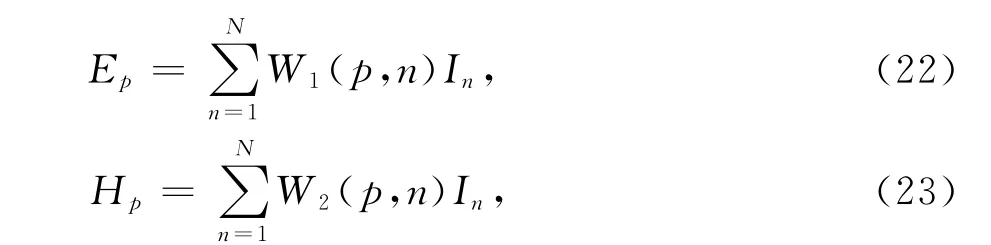
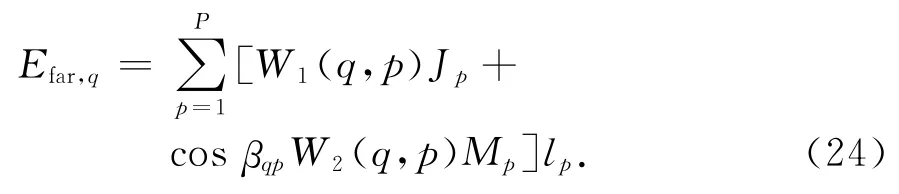
因为矩阵W1、W2代表了辐射场与空间位置的关系，并不受源电流特性的影响，所以能够预先计算以提升求解速度.这使在较短时间内完成大量优化工作成为可能.

2 优化算例与结果分析

优化一个包含线阵的正切卵形天线罩系统.等幅线阵单元数N为16，间距d为0.5λ，频率为13 GHz.天线罩长L为24λ，底部直径D为12λ，罩厚为0.282 3λ，相对介电常数为4，损耗正切为0.015.分别用连续PSO与离散PSO进行直接优化与基于先验信息的优化.适应度函数的权重因子w1取3，w2取1.带罩天线系统的扫描角范围选取［0°，50°］，连续相位优化的补偿范围为［-10°，10°］.离散相位优化中，移相器位数取4，相位补偿位数取1，这样相位补偿值将为0°或22.5°.相移K的调节范围为［-180°，180°］，K在优化中做12位离散，取值间隔小于0.1°.

差方向图瞄准误差的优化效果如图2所示.对于连续相位情况，优化后系统的瞄准误差低于0.001°，对于4位数字相位情况，优化后瞄准误差低于0.03°.

表1列举了部分扫描角处的详细相位参数.由于4位移相器有16种状态，数字相位在这里用十六进制数字表示.12位离散的最优相移量Kbest由3位十六进制数字代表.由于Kbest的作用，虽然只进行了一位相位补偿，优化前后阵元的相位状态有较大差别.

表1 差方向图优化前后的部分相位参数

图3比较了不同离散相位优化方法得到的瞄准误差.不考虑先验信息，直接优化后的最大瞄准误差为0.056°，与基于先验信息优化得到的0.03°相差不大.将相移K固定为0，优化后最大瞄准误差达到0.7°.可见通过优化相移K，能显著降低带罩天线系统的瞄准误差，这也说明低位移相器数字量化误差对系统瞄准误差的贡献不容忽视.

图4给出了连续相位优化情况下，扫描角15°的优化中，最优解对应的适应度函数曲线.无论是否采用先验优化方法，PSO的初始粒子群都是随机生成的，这里直接优化得到了更好的初始最优值.之后先验优化便迅速收敛，20步迭代即达到稳定；而直接优化要到46步迭代才获得最优解.

15°扫描角时，离散相位系统优化前后的辐射方向图如图5所示，优化并没有改变方向图的分布趋势，主瓣宽度也未受到影响，远离辐射方向处的旁瓣电平略有提高.

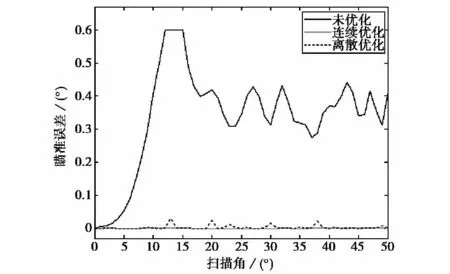
图2 带罩天线优化前后的差方向图瞄准误差

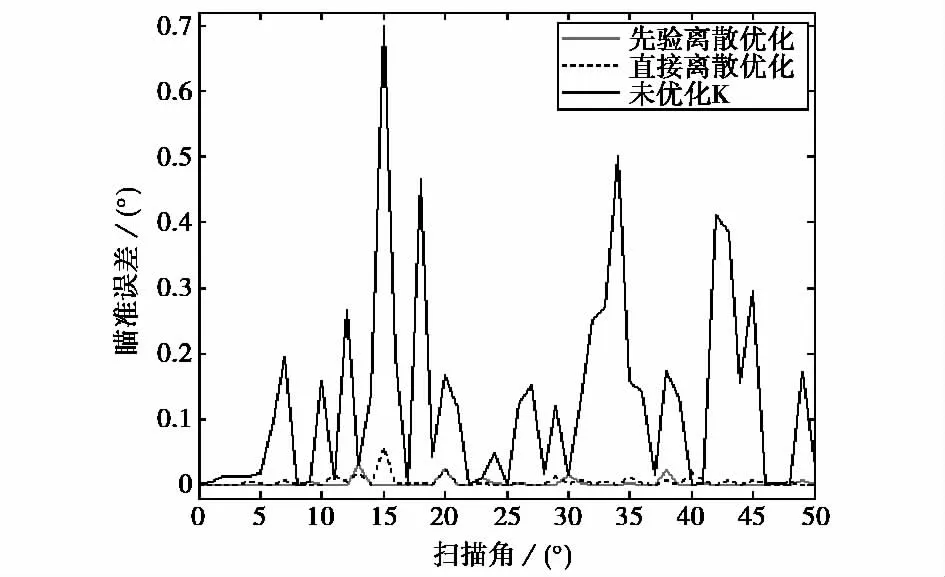
图3 离散相位优化中先验信息修正及K的影响

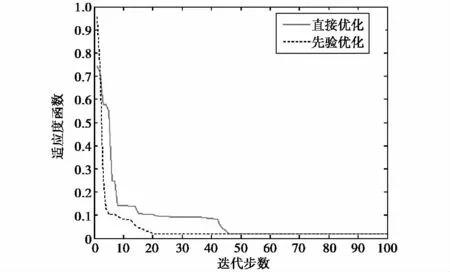
图4 先验信息修正对收敛速度的影响

图5 离散优化前后15°指向的方向图比较

3 结 论

本文提出了一种新的天线罩瞄准误差快速优化技术.基于小规模阵列与低位数字移相器，通过带有偏移量优选技术的离散PSO方法，调节阵元相位补偿值，实现瞄准误差的精确优化.同时为提高效率，提出了基于先验信息的快速优化方法，以及基于辐射关系矩阵的数值计算加速方法.虽然本文的公式推导与算例分析限于二维情况，但其思想完全适用于三维天线罩的优化工作.

［1］彭望泽.防空导弹天线罩［M］.北京：宇航出版社，1993.

［2］戎 华，曲晓飞，杨美建，等.关于减小天线罩瞄准误差的补偿方法研究［J］.系统工程与电子技术，2005，27（6）：1135-1137.RONG Hua，QU Xiaofei，YANG Meijian，et al.Research on the compensation method of decreasing a radome’s boresight error［J］.Systems Engineering and Electronics，2005，27（6）：1135-1137.（in Chinese）

［3］HSU F，CHANG P R，CHAN K K.Optimisation of two-dimensional boresight error performance using simulated annealing technique［J］.IEEE Trans Antennas and Propagat，1993，41（9）：1195-1203.

［4］傅文斌，陈忠宽，常以涛.夹层天线罩壁电性能的多目标遗传优化［J］.电波科学学报，2005，20（3）：289-294.FU Wenbin，CHEN Zhongkuan，CHANG Yitao.Multi-objective optimization of electric performance of sandwich antenna radome wall using genetic algorithm［J］.Chinese Journal of Radio Science，2005，20（3）：289-294.（in Chinese）

［5］任 宁.阵列天线的优化综合技术研究［D］.西安：西北工业大学，2010.REN Ning.Research on the Optimization and Synthesis Technique of Array Antennas［D］.Xi’an：Northwestern Polytechnical University，2010.（in Chinese）

［6］李知新.相控阵天线的一种新的馈相方法［J］.电子学报，1981，3（2）：87-88.LI Zhixin.A new method of phase feeding in phased arrays［J］.Acta Electronica Sinica，1981，3（2）：87-88.（in Chinese）

［7］JIANG W，GUO Y，LIU T，et al.Comparison of random phasing methods for reducing beam pointing errors in phased array［J］.IEEE Trans.Antennas and Propagat.，2003，51（4）：782-787.

［8］CIATTAGLIA M，ZUCCA M.Efficient beam pointing algorithm for phased arrays with low phase shifter control［C］／／IEEE Phased Array Systems ＆Technology International Symposium，2010，10：137-139.

［9］万国宾，万 伟，汪文秉.雷达罩电性能的优化［J］.系统工程与电子技术，2000，22（5）：40-42.WAN Guobin，WAN Wei，WANG Wenbing.Studies on electrical design of airborne radomes［J］.Systems Engineering and Electronics，2000，22（5）：40-42.（in Chinese）