一类具有垂直传染率的SIRS模型的稳定性分析

郭金生，刘旭峰，唐玉玲

(河西学院 数学与统计学院，甘肃 张掖 734000)



一类具有垂直传染率的SIRS模型的稳定性分析

郭金生，刘旭峰，唐玉玲

(河西学院 数学与统计学院，甘肃 张掖 734000)

摘要：讨论了一类具有垂直传染结构及其非线性传染率的SIRS传染病模型,给出了基本再生数R0,借助构造Liapunov函数及相关理论,分析了平衡点的局部渐近稳定性及全局渐近稳定性.

关键词：非线性传染率; 局部渐近稳定性; 全局渐近稳定性

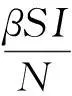
1预备知识

定义1[9]设n维自治微分方程

的解为x(t)=(x1(t),x2(t),…,xn(t)),V(x(t))是t的复合函数,关于t求导得

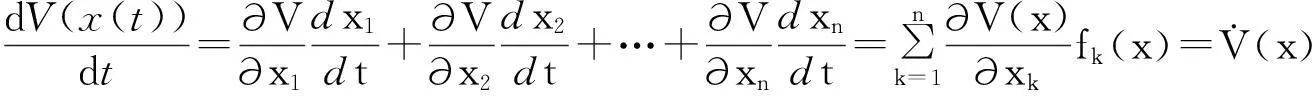
其中，f(x)=(f1(x1,x2,…,xn),f2(x1,x2,…,xn),…,fn(x1,x2,…,xn)),称V′(x)为V(X)沿着自治方程轨线的全导数.

定义2[9]考虑自治系统

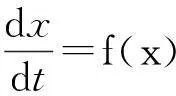
(1)

其中

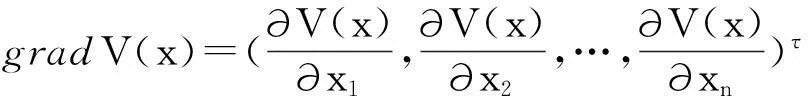
f(x)=(f1(x1,x2,…,xn),f2(x1,x2,…,xn),…,fn(x1,x2,…,xn))τ，

则称V是系统(1)的Liapunov函数.

M是系统(1)在E中的最大不变集,若M={x*},这里f(x*)=0,则称系统(1)的平衡点x*在Ω内是全局吸引的.

引理2[10](Routh-Hurwitz判据) 考虑多项式方程

a0λn+a1λn-1+a2λn-2+…+an-1λ+an=0，

式中an>0,其一切根具有负实部的充要条件是下列不等式同时成立:

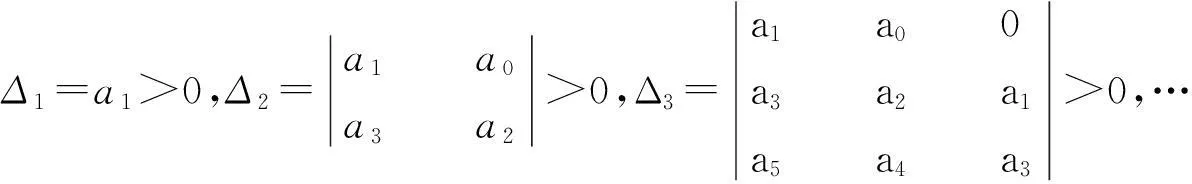
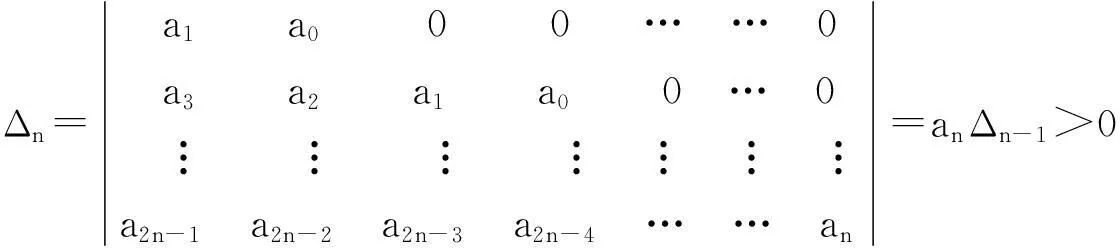
其中,当i>n时,ai=0.

引理3[10]若线性系统的系数矩阵A的所有特征值均具有负实部,则系统的零解是局部渐近稳定的.

引理4[10]若系统(1)的零解是局部渐近稳定的,且其吸引域是Rn或Rn中的一个确定区域时,称系统(1)的零解是全局渐近稳定的.

引理 5[10]设V(x)是Rn上的正定函数,有无穷大下界,V(x)沿着系统

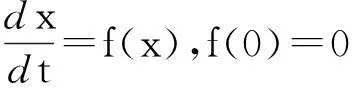
(2)

轨线的全导数半负定,且集合{x|V′(x)=0 }不含系统(2)中任何正半轨线,那么系统(2)的零解是全局渐近稳定的.

2模型建立

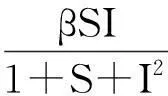
基于以上假设可得到具有非线性传染率及垂直传染结构的SIRS模型:

(3)

设t时刻的人口总数为N(t)=S(t)+I(t)+R(t),其中S(t),I(t),R(t)分别为时刻易感者类,染病者类和恢复者类的人口数量.

则由系统(3)把3个方程相加知

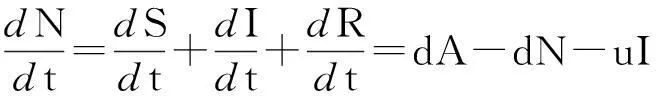
由上式可知当疾病不存在时,u=0 (即无因病死亡率),此时则有

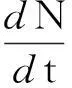
计算此微分方程可得

N(t)→A(t→+∞) ，

因此系统(3)的正向不变集为

T={(S,I,R)|S,I,R≥0,S+I+R≤A}.

记基本再生数

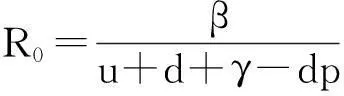
R0即为在假设发病初期人人均为易感者情况下,在平均染病期内一个病人传染的易感者类人数,其中1/(u+d+γ-dp)表示平均患病期.

3平衡点稳定性分析

P(S,I,R)=0,Q(S,I,R)=0,W(S,I,R)=0,

则当R0>1时有

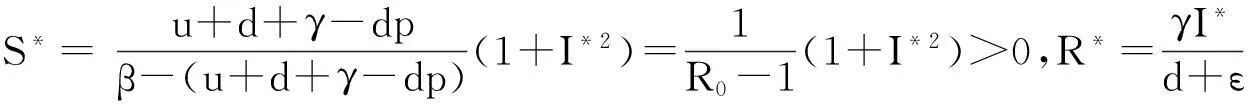
定理1当R0≤1时,系统(3)有唯一的无病平衡点P0=(S0,I0,R0),其中

S0=A,I0=0,R0=0,

当R0>1时,系统既有无病平衡点P0,又有地方病平衡点P*(S*,I*,R*),其中

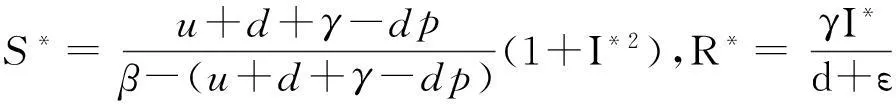
且I*是方程

f(I)=dA-dS+εR-(u+d+γ)I=0

在(0，A)上的唯一正解.

证明在系统(3)中令

P(S,I,R)=0,Q(S,I,R)=0,W(S,I,R)=0,I=0,

则有

S0=A,I0=0,R0=0，

故系统(3)在正向不变集T上有唯一的无病平衡点

P0(S0,I0,R0)=(A,0,0).

若仅令

f(I*)=dA-dS*+εR*-(u+d+γ)I*=0，

则在(0，A)上,当R0>1时

f(0)=dA-dS*=d(A-S*)>0，

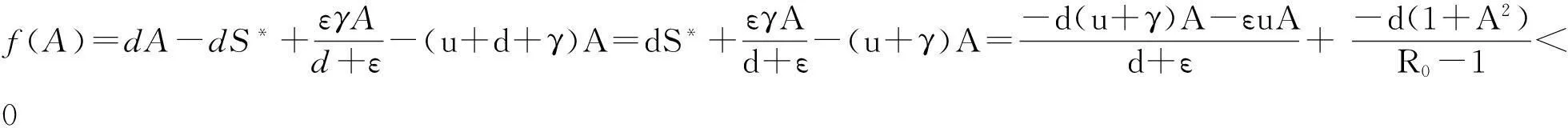
又

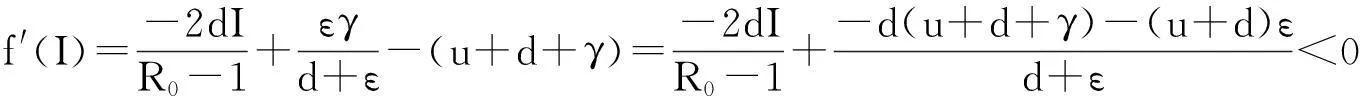
即f(I)关于I是严格单调递减函数,则I*是方程f(I)在(0,A)上的唯一正解.

故系统(3)在正向不变集T上有唯一的地方病平衡点

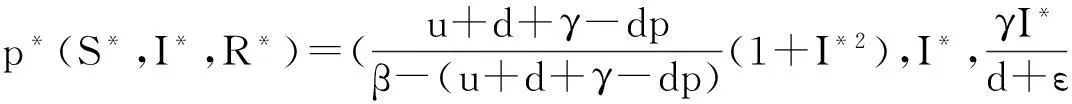
定理2当R0≤1时,系统(3)的无病平衡点P0=(S0，I0，R0)是局部渐近稳定的;当R0>1时,系统的地方病平衡点P*(S*，I*，R*)是局部渐近稳定的.

证明系统(3)的雅克比行列式为

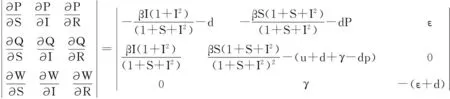
那么系统(3)在P0=(S0，I0，R0)点的特征方程为

即

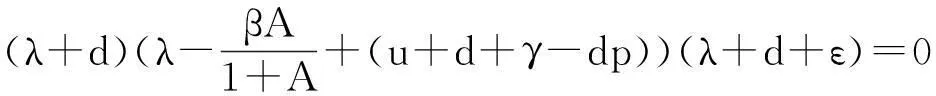
则有特征根

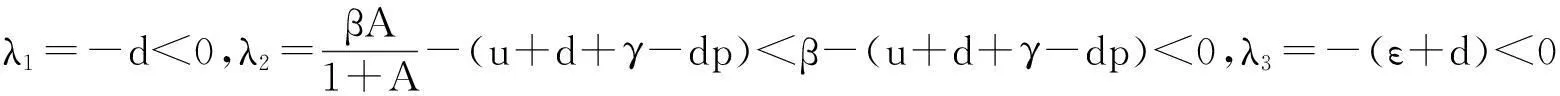
即R0≤1时特征方程的所有特征根均为负值,则系统(3)在P0=(S0，I0，R0)点是局部渐近稳定的.

当R0>1时,假设系统(3)在点P*(S*,I*,R*)处的特征方程为

λ3+a1λ2+a2λ+a3=0，

通过化简可知

a1=m+2d+ε+n0-n,

a2=(m+d+n0-n)(d+ε)+d(n0-n)+mn0+dpm，

a3=(mn0+dn0-dn)(d+ε)+dpm(d+ε)+mεγ，

其中

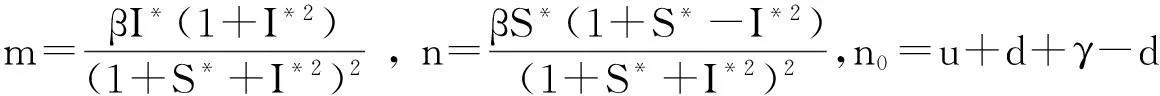
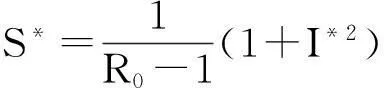
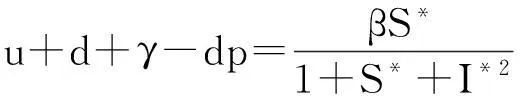
即有

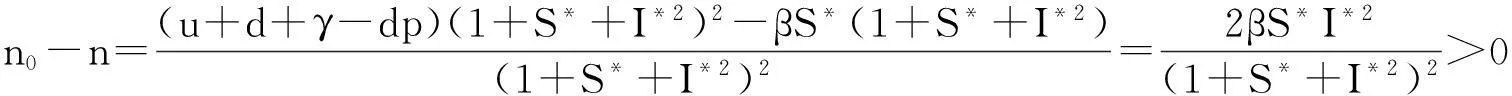
显然有a1，a2，a3>0.

由假设d>γ或ε>γ知

a1a2-a3=(m+2d+ε+n0-n)(m+d+n0-n)(d+ε)+(m+d+n0-n)(dn0-dn+mn0)+

dpm(m+d+n0-n)-mεγ>0.

则由Routh-Hurwitz条件知系统(3)在点P*(S*,I*,R*)是局部渐近稳定的.

定理3当R0≤1时,系统(3)的无病平衡点P0=(S0，I0，R0)是全局渐近稳定的;当R0>1时，系统的地方病平衡点P*(S*,I*,R*)是全局渐近稳定的.

证明当R0≤1时,构造Liapunov函数

V(t)=I(t)，

那么在P0=(A,0,0)点,V(t)沿着系统(3)轨线的导数为

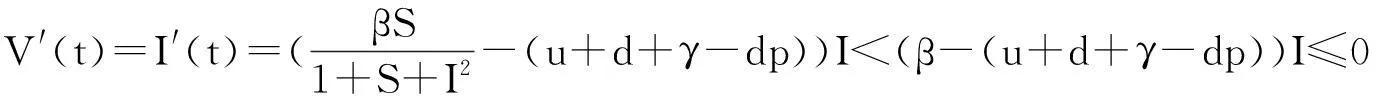
显然

那么系统(3)在E中的最大不变集为

M={I=0} .

考虑自治系统

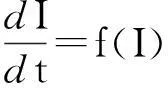
由于

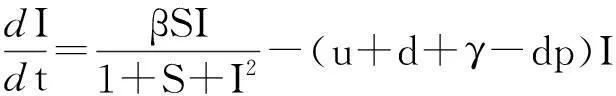
则f(0)=0,那么平衡点P0=(S0,I0,R0)在开集Ω⊂T内是全局吸引的.

结合P0=(S0,I0,R0)点的局部渐近稳定性,则系统(3)当R0≤1时在P0点是全局渐近稳定的.

当R0>1时,结合文献[3]中SIRS模型的V函数定义方法可定义

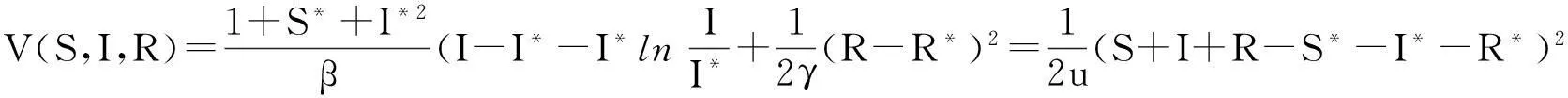
那么对所有的(S*,I*,R*)≠(S,I,R)均有V(S,I,R)>0.

又因为

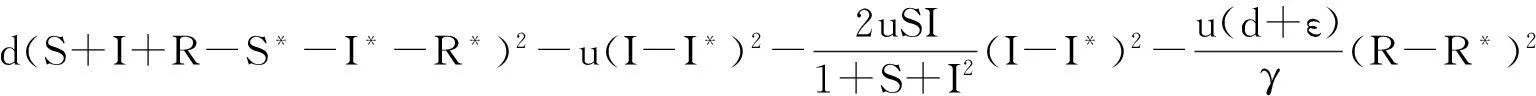
那么对所有的(S*,I*,R*)≠(S,I,R)均有V′(S,I,R)<0,则系统(3)在P*(S*,I*,R*)点是全局渐近稳定的.

4小结

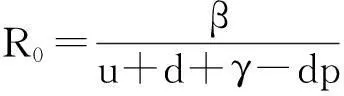
参考文献：

[1] 卢雪娟,王伟华,堵秀风.具有非线性传染率的SEIS传染病的研究[J].西北师范大学学报， 2010,46(5):6-9.

[2] 王拉娣,李建全.一类带有非线性传染率的SEIS传染病模型的定性分析[J].应用数学和力学学报,2006,28(5):591-596.

[3] 王拉娣.一类含有非线性传染率的传染病的全局稳定性[J].应用数学与计算机学报，2004,18(1):52-56.

[4] Liu W M, Levin S A. Influence of nonlinear incidence rates upon the behave of SIRS epidemiological model [J].Math.Biol,1986,23(1):187-204.

[5] Han L T，Ruan S L，Ma Z E.Stabiity of an SIRS epidemic model of two competitive species [J] Biol,2003,18(1):21-26.

[6] Wang W ，Ruan S.Sinulating the SIRS outbreak in Beijing with limited date[J].Theoret Biol,2004,227(2):369-379.

[7] 高淑京,滕志东.一类具有饱和传染力和常数输入的SIRS脉冲接种模型[J].生物数学学报,2008,23(2):208-217.

[8] 郭金生,祝进业,唐玉玲.具有一类具有非线性传染率的SEIS传染病模型的定性分[J].贵州大学学报,2013,30(5):4-8.

[9] 马知恩,周义仓.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.

[10] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

Stability Analysis of a Kind of SIRS Model with Vertical Transmission Rate

Guo Jinsheng, Liu Xufeng, Tang Yuling

(School of Mathematics and Statistics, Hexi University, Zhangye 734000，China)

Abstract：In the report, a kind of SIRS epidemic model with vertical transmission and nonlinear incidence rate was discussed, and the basic reproduction numberR0was proposed, based on the construction of Liapunov function and related theory, the local and global asymptotic stability of the equilibrium point was analyzed.

Keywords：nonlinear incidence rate; local asymptotic stability; global asymptotic stability

中图分类号：O 175.1

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0020

文章编号：1004-1729(2015)02-0109-06

收稿日期：------------------------ 2014-11-28基金项目： 河西学院青年基金 (QN2014-12)

作者简介：郭金生(1979-)，男，甘肃静宁人，硕士，讲师.通信作者： 唐玉玲(1980-)，女，甘肃民勤人，硕士，讲师，研究方向：计算数学，E-mail：tyl0316@163.com