关于伪Smarandache函数的一个混合均值

王曦浛，高　丽，鲁伟阳

(延安大学 数学与计算机科学学院，陕西 延安 716000)



关于伪Smarandache函数的一个混合均值

王曦浛，高丽，鲁伟阳

(延安大学 数学与计算机科学学院，陕西 延安 716000)

摘要：对任意的正整数n，著名的伪Smarandache函数Z(n)定义为最小的正整数m使得n|m(m+1)/2，即Z(n)=min{m:n|m(m+1)/2,mN}.对任意的正整数n，算术函数定义(1)=0,当n>1且n=p1α·p2α...pkα为n的标准分解式时，利用初等方法和解析方法研究了伪Smarandache函数Z(n)与算术函数的混合均值问题，并得到一个较强的渐近公式.

关键词：伪Smarandache函数； 算术函数； 混合均值； 渐近公式

对任意的正整数n，著名的伪Smarandache函数Z(n)定义为最小的正整数m使得n|m(m+1)/2，即

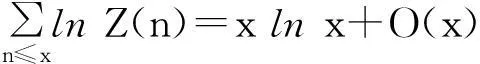
ChengLin[4]证明了渐近式

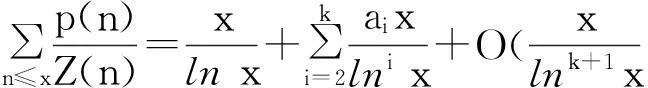
笔者曾讨论了Smarandache双阶乘函数与伪Smarandache函数的复合函数Sdf(Z(n))均值[5]，即证明了

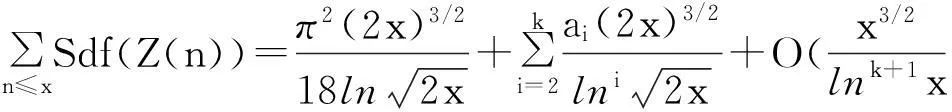
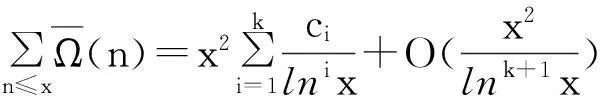
(1)

其中，ci(i=1,2,…,k)为可计算的常数且c1=π2/12.

定理1设k≥2是给定的正整数，则对任意的实数x≥2，有渐近式

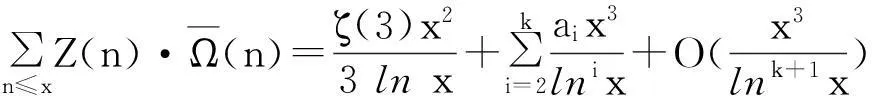
(2)

其中，ai(i=1,2,…,k)为可计算的常数.

1相关引理

引理1[7-8]对任意的正整数n和k，有1≤Z(n)≤2n-1，当n=2k时，Z(n)=2n-1；当n=pk时，Z(n)=n-1，其中p为奇素数；若n为任意的合数时，Z(n)=max{Z(m):m|n}.

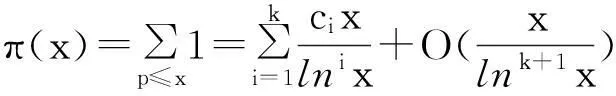
2定理的证明

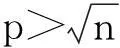
(3)

其次在集合B中讨论，由引理1知

(4)

由引理2及Abel求和公式[10]可得

(5)

(6)

其中，ai(i=1,2,…,k)为可计算的常数.

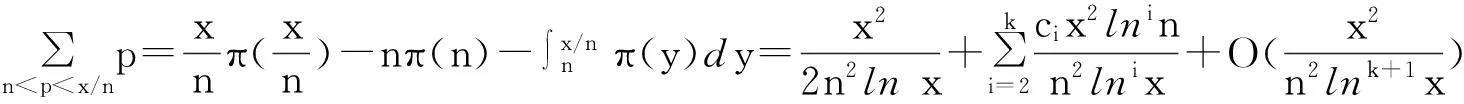
(7)

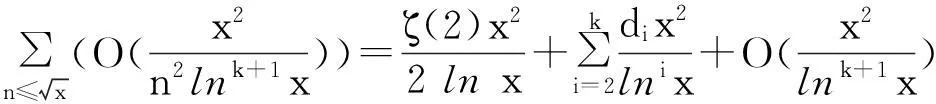
(8)

其中，di(i=1,2,…,k)为可计算的常数.

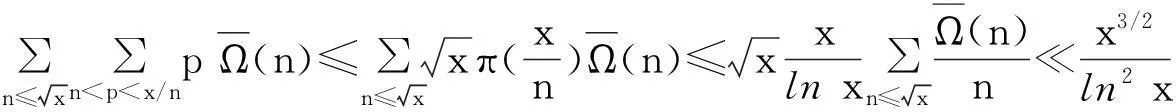
(9)

(10)

结合式(4)，(6)，(8)，(9)和(10)可得

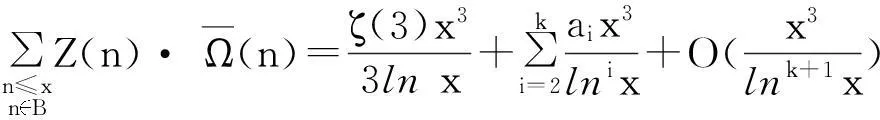
其中，ai(i=1,2,…,k)为可计算的常数.

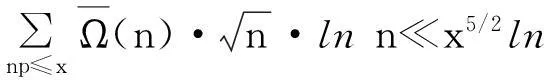
综上可知，

，

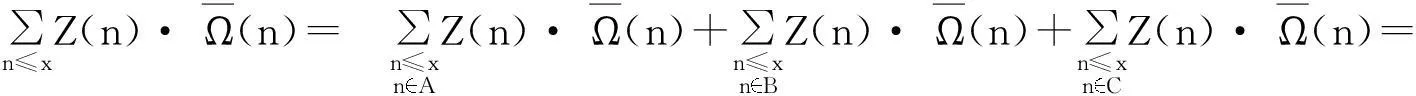
其中，ai(i=1,2,…,k)为可计算的常数.

证毕.

参考文献：

[1] Kenichiro K. Comments and Topics on Smarandache Notions and Problems[M]. Aarhus: Erhus University Press,1996.

[2] Majumdar A A K. A note on the Pseudo-Smarandache function[J]. Scientia Magna, 2006, 2(3):1-25.

[3] Luo Yuanbing. On the pseudo Smarandache function[J]. Scientia Magna, 2007, 3(4):48-50.

[4] Cheng Lin. On the mean value of the Pseudo-Smarandache function[J]. Scientia Magna, 2007, 3(3):97- 100.

[5] 鲁伟阳，高丽，郝虹斐. 关于Smarandache双阶乘函数与伪Smarandache函数的混合均值[J]. 江西科学, 2014, 32(2): 189-191，251.

[6] 薛社教. 一个新的算术函数及其均值[J]. 纯粹数学与应用数学, 2007, 23(3): 351-354.

[7] Pinch R. Some properties of the Pseudo Smarandache function[J]. Scientia Magna, 2005, 1(2):167-172.

[8] 马荣. Smarandache函数及其相关问题研究[M]. Columbus : The Educational Publisher, 2012.

[9] 潘承洞, 潘承彪. 素数定理的初等证明[M]. 上海: 上海科学技术出版社, 1988.

[10] Tom M. Apostol. Introduction to analytic number theory[M]. New York: Spring-Verlag, 1976.

A Hybrid Mean Value of the Pseudo-Smarandache Function

Wang Xihan, Gao Li, Lu Weiyang

(College of Mathematics and Computer Science, Yan’an University, Yan’an 716000，China)

Abstract：For any positive integern, the famous Pseudo-Smarandache functionZ(n) is defined as the smallest positive integer m such thatn|m(m+1)/2, that isZ(n)=min{m:n}m(m+1)/2,mN}.Andforanypositiveintegern,thearithmeticalfunctionΩ(n)isdefinedasΩ(1)=0,ifn>1andn=p1α·p2α...pkαbethefactorizationofnintoprimepowers,(n)=α1p1+α2p2+…+αkpk.TheelementarymethodandanalyticmethodwereperformedtostudythehybridmeanvalueprobleminvolvingthePseudo-SmarandachefunctionZ(n)andthearithmeticalfunction(n),andashaperasymptoticformulawasproposed.

Keywords：Pseudo-Smarandachefunction;arithmeticalfunction;hybridmeanvalue;asymptoticformula

中图分类号：O156.4

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2015.0017

文章编号：1004-1729(2015)02-097-03

收稿日期：------------------------ 2015-01-21基金项目： 陕西省科技厅科学技术研究发展计划项目(2013JQ1019); 延安大学校级科研计划项目-引导项目(YD2014-05); 延安大学研究生教育创新计划项目.

作者简介：王曦浛(1990-), 女, 陕西乾县人, 2014级硕士研究生.通信作者： 高丽(1966-), 女, 陕西绥德人, 教授, 硕士生导师, 研究方向：数论、函数论，E-mail:yadxgl@163.com