采用混合材料的离心风机转子的模态分析

叶福民，赵海东，陈 石

(江苏科技大学机械工程学院，江苏镇江212003)

离心风机广泛应用于煤炭、钢铁、电力、农业等各个领域，成为我国国民经济重要的机械设备，在现代化工业中用途广泛，其性能好坏对节能降耗影响重大［1－4］.离心风机在运行过程中由于叶轮的不平衡量引起整个风机转子的振动，影响周围环境，导致工作效率下降［5－6］.

近年来，国外学者对离心风机的模态和临界转速等进行了大量研究.我国关于离心风机转子模态分析研究较少，传统方法是在实验基础上，用实验和理论结合的方法来处理振动问题［7］，这样方法使计算过程比较繁琐，计算周期比较漫长.有限元软件ANSYS的出现能够快速准确的进行模态分析，大大提高了研究工作的效率.文献［8］中利用有限元ANSYS分析了轴流风机的振动特性，得到了固有频率和振型，并且通过实验对计算结果进行了验证.文献［9］中对轴流风机进行模态分析，得到叶片的固有频率和在空气激振力下的谐波频率.

文中通过对比不同材料离心风机转子固有频率和振型，得出混合材料转子不会发生共振的结论，为离心风机的设计提供参考.

1 离心风机转子有限元模型

1.1 模态分析

转子旋转时，都会由于质心偏离产生横向振动，这种振动在某些转速上显得异常强烈，这些转速称为临界转速.为防止机器工作发生共振，临界转速应适当偏离工作转速.传统动力学用传递矩阵法求解，避免不了陀螺效应的影响，使计算结果缺乏准确性和说服力.ANSYS能解决动力学分析中的陀螺效应，使动力学分析变得实际和有效.根据弹性力学有限元知识可知，N自由度的转子系统在静止状态下运动微分方程为［10］:

式中:M，C，K分别为质量矩阵、阻尼矩阵和刚度矩阵;Cg为陀螺效应矩阵;Ft为激振力列阵.

在转动状态下的运动微分方程为:

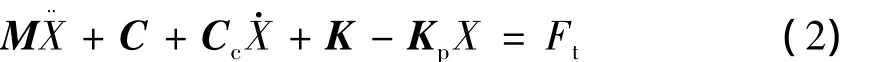
式中:Cc，Kp分别为哥氏效应矩阵和旋转软化效应刚度矩阵.

阻尼主要是减小共振点的幅值，对频率没有多大影响，这里忽略阻尼的影响.当不存在外力作用，即Ft为零时，对于求解多自由度模态的固有频率，可通过无阻尼的振动微分方程求解:

通过一些简谐振动的叠加，其自由运动简谐方程为:

式中:ωni为第i阶振型的固有频率;Xi为i阶位移列阵;Ai代表i阶位移最大值.将式(4)代入式(3)得到:

1.2 有限元模型

离心风机转子模型由2个叶轮、垫支轴、2个轴盘、轴套6个部分组成.利用UG建立与实物对等的三维模型并通过约束完成装配，如图1所示.

通过中间格式CATIA导入ANSYS进行有限元网格划分，由于该模型是装配体，导入之后需要进行GLUE定义体和体之间的接触.自由网格是自动化最高的网格划分技术之一，可以在体上自动生成四面体网格.SOLID187是一个高阶三维10节点四面体固体结构单元，单元通过10个节点来定义，每个节点有3个沿着X，Y，Z方向平移的自由度，能够很好的模拟不规则模型.文中以SOLID187单元类型，10mm为单元大小进行自由网格划分，划分的网格模型共224203个节点，116123个单元，如图2所示.

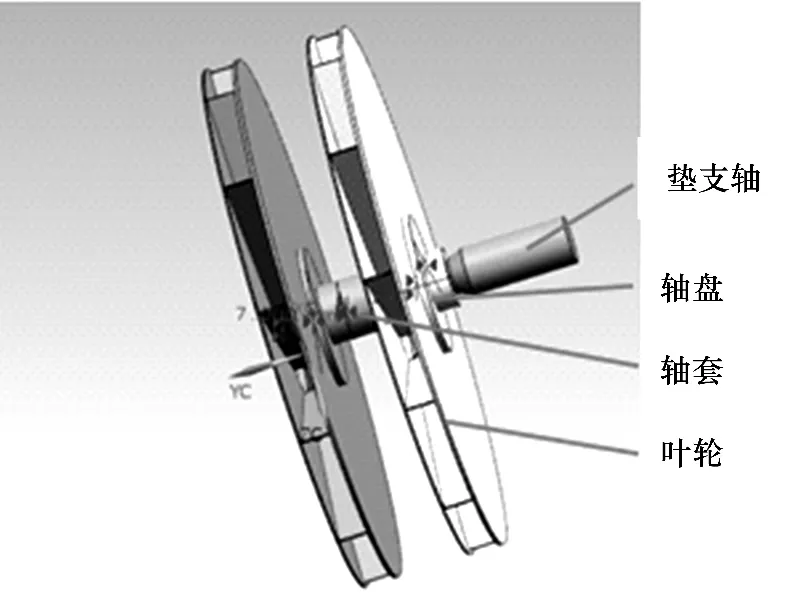
图1 转子的三维模型Fig.1 Three-dimensional model of the rotor

图2 转子的有限元网格Fig.2 Rotor finite element mesh

2 计算结果及分析

2.1 风机自由模态

离心风机的额定转速为n=2 900 r/min，由频率(k分别取正整数 1，2，3，…代表风机的基频及其倍频)计算可知风机的基频为48.33 Hz，基频的 1，2，3，4，…，10 倍频分别为 48.33，96.66，144.99，193.32，…，483.3 Hz.当叶片数目为 12，也即k=12时，风机的叶频为579.96 Hz.

自由模态分析是模态分析的一个重要组成部分，它不考虑任何约束的影响，得到的是结构本身的固有特性.通过自由模态的分析，可以对结构本身的尺寸、材料、振动情况等有个大概的了解.以工程应用较多的Q235材料作为对象，其弹性模量E=2.4×105MPa，泊松比 μ=0.3，材料密度 ρ=7.8×10－9t/mm.首先确定离心风机转子在自由模态下前20阶固有频率和相对应的振型图，固有频率如表1所示，因为篇幅原因，只选出代表性的6，7阶振型图.

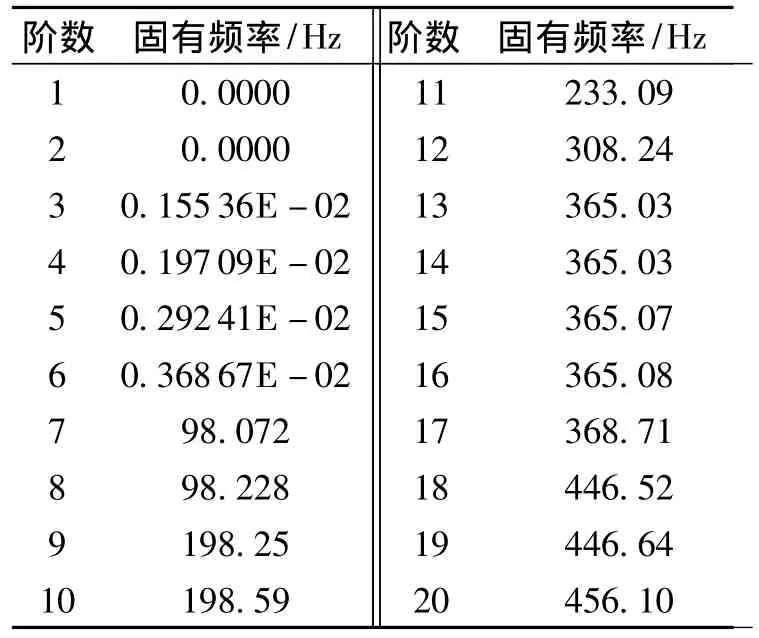
表1 转子自由模态频率Table 1 Rotor freedom modal frequencies

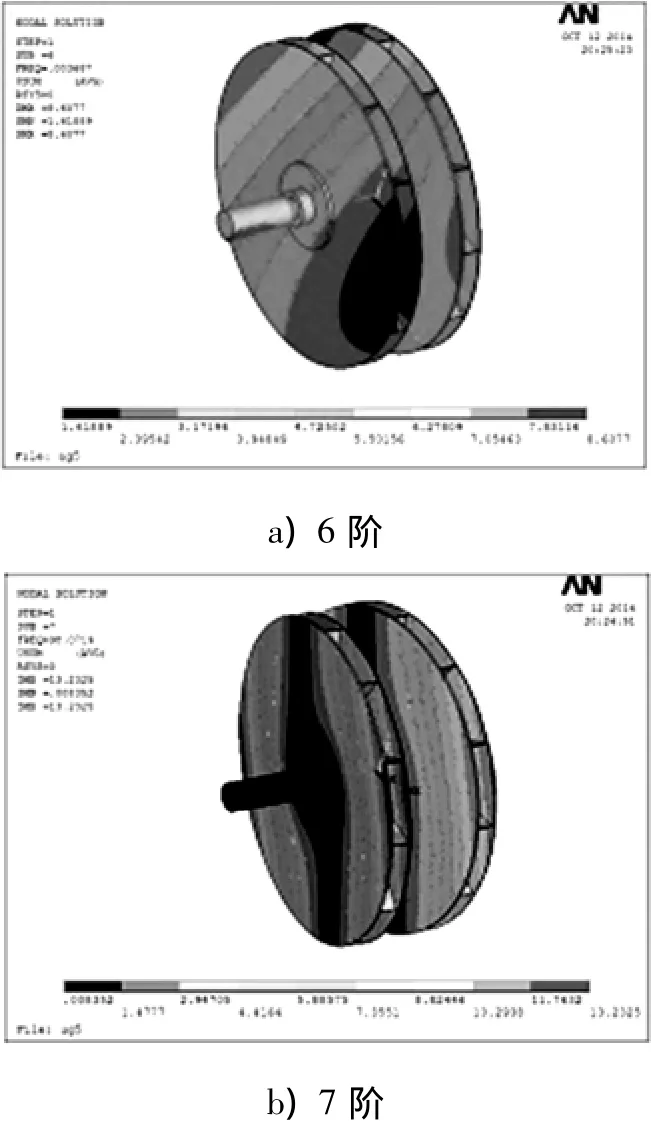
图3 转子自由模态的振型Fig.3 Vibration mode map of the rotor free modal

由表1可知，转子不受任何约束和外在力的情况下，有X，Y，Z3个方向的平动和转动，6个自由度都存在独立的刚体运动，所以前6阶接近于零.由图3可知道因为前6阶频率接近于零，振型图不存在明显的变形，最大位移在边缘处，7阶以后振型图有明显变形，最大位移有所改变.经验证，自由模态下各阶固有频率都不等于或不接近风机的基频及其倍频或叶频，不会出现共振现象.

2.2 不同材料转子模态分析

工程应用中，风机工作时受各种约束和外在的载荷作用.根据风机实际工作情况，在原来轴承支撑的地方加X，Y，Z方向的固定约束，如图4所示.

图4 约束的施加Fig.4 Applying constraints

2.2.1 Q235材料

Q235是普通碳素结构钢，是常见的风机制造材料，屈服强度σ≤235 MPa，材料弹性模量E=2.4×105MPa，泊松比 μ=0.3，材料密度 ρ=7.8×10－9t/mm.在受约束的情况下用ANSYS进行模态分析，得出前10阶固有频率，如表2所示.因为X，Y对称性，1和2阶，4和5阶频率接近，振型相似，所以只列出1，3，5阶振型图做研究，如图5所示.

表2 Q235材料转子的固有频率Table 2 Natural frequency of the rotor Q235 material

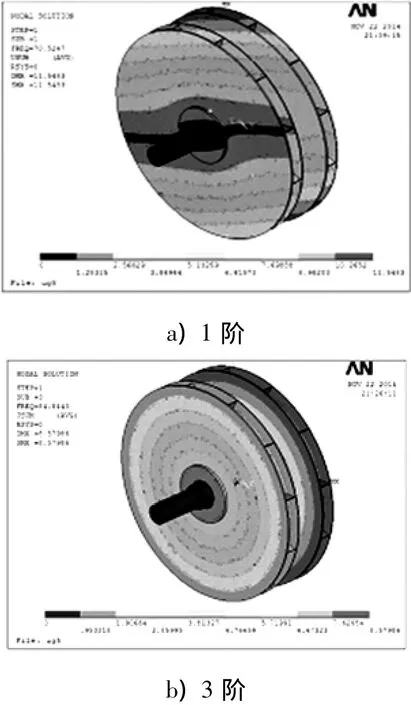
图5 Q235材料转子的振型Fig.5 Vibration mode map of the rotor Q235 material

图5反应的是前10阶频率中的1，3，5阶频率振型图，第1阶频率为70.525 Hz，沿着直径表现出向两边的条形振动，最大振幅为第1级叶轮边缘，大小为11.548 3 mm.第3阶频率为84.844 Hz，表现以叶轮中心向两边的环形振动，最大振幅也处在第1级叶轮边缘处，大小为8.579 9 mm.第5阶频率98.306 Hz，沿着轴径波浪式波动振动，最大振幅在第2级叶轮边缘处，大小为13.6758 mm.由于最大振幅代表的各阶模态对应的模态振幅反映转子振动特性，因为没有激励力，所以不是真实位移，这里的大小没有实际意义.根据前10阶振型图可知，转子在第9阶241.52 Hz与5倍基频241.65 Hz接近，容易引起共振.

2.2.2 铸铝

转子的材料改用铸铝，因为铸铝的特点是成分简单，容易熔炼和铸造，铸造性能好，气密性好，焊接和切削加工性能也好.其参数如下，材料弹性模量E=0.73×105MPa，泊松比 μ=0.33，材料密度ρ=2.8×10－9t/mm，建立带有边界条件的有限元模型，得出前10阶固有频率和对应的振型，1，3，5阶振型图如图6所示.

表3 铸铝转子固有频率Table 3 Cast aluminum rotor natural frequency

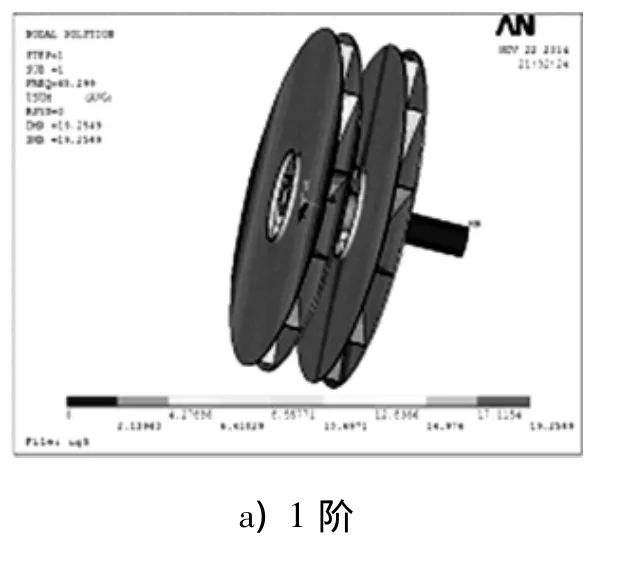
图6 铸铝转子振型Fig.6 Cast aluminum rotor modal map

由振型图可知，1，3，5阶频率分别为65.299，77.229，91.437 Hz，振动最大振幅分别为19.2549，14.3115，22.819 6 mm.转子在第10阶288.83 Hz与6倍基频289.98 Hz接近，容易引起共振，需要对转子的结构进行修改.

2.2.3 混合材料

根据以上分析，上述两种材料都存在共振现象，需要对结构参数进行修改.该型离心风机转子是由不同子部件装配而成，文中用以上两种材料分别用于不同的子部件，也即称为混合材料转子.因为垫支轴需要传递扭矩、弯矩等，要满足强的刚度要求，轴套和轴盘也承受较大的力，因而都采用Q235钢材料;叶轮用铸铝材料，这样不仅可以减轻整体重量，更能保证转子的整体结构强度.铸铝和钢的各项参数上文已经提到.利用ANSYS的模态分析得出前10阶固有频率和对应的振型，提取1，3，5阶振型图分析.

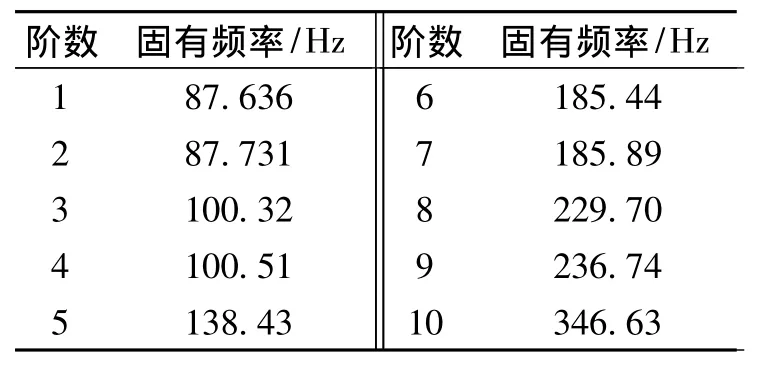
表4 混合材料转子固有频率Table 4 Natural frequency of the rotor hybrid materials

图7 混合材料转子振型Fig.7 Material mixing rotor vibration mode map

第1阶振型表现出两个叶轮都存在条形振幅，第3阶波浪型振幅并伴随着扭转的振动，第5阶环形振幅，整体振型接近钢材料和铸铝材料.分析结果表明这种混合材料转子，能满足强度要求，也能减轻重量，得出的前10阶固有频率不与基频及其倍频或者叶频相同或者接近，避免了共振的发生.

3 结论

1)采用ANSYS建立转子的有限元模型，对自由状态下转子进行模态分析，结果显示自由模态下不存在共振.

2)在受约束状态下，分别对Q235、铸铝、混合材料3种材料转子进行模态分析，得到固有频率和对应振型，分析结果显示Q235和铸铝都存在固有频率接近基频的倍频，容易引起共振，混合材料各阶频率不接近风机基频及其倍频或叶频，很好的避免了共振的发生.

3)所做研究为避免离心风机转子共振提出一种新的方法，也为离心风机的设计与转子动力学分析提供参考.

References)

［1］ 石雪松，丘明杰.新型工业化时期我国离心风机行业发展趋势分析［J］.通用机械，2009(1):15－18.Shi Xuesong，Qiu Mingjie.Development trend analysis of our centrifugal fan industry in new industrial era［J］.General Machinery，2009(1):15 －18.(in Chinese)

［2］ 叶福民，冯露，陈文杰，等.离心风机的内部流场数值模拟及噪声预估［J］.江苏科技大学学报:自然科学版，2014，28(2):155 －157.Ye Fumin，Feng Lu，Chen Wenjie，et al.Numerical simulation of inside flow field and noise forec－ast for the centrifugal fan［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2014，28(2):155 －157.(in Chinese)

［3］ 李燕平，吕新民.农用风机叶轮的有限元分析［J］.农机化研究，2012(4):207－209.Li Yanping，Lü Xinmin.Finite element analysis of the impeller of agricultural fan［J］.Agricultural Mechanization Research，2012(4):207 －209.(in Chinese)

［4］ 刘艳艳.风筛式清选装置中离心风机的试验研究及仿真分析［D］.江苏镇江:江苏大学，2009.

［5］ 林忠.风机叶轮与轴不平衡振动故障分析与治理研究［J］.仪表技术，2009(9):36－38.Lin Zhong.Analysis and research on the unbalanced vibration fault of fan impeller and shaft system［J］.Instrumentation Technology，2009(9):36 －38.(in Chinese)

［6］ 杨涛，任永，刘霞，等.风力机叶轮质量不平衡故障建模及仿真研究［J］.机械工程学报，2012，48(6):130－135.Yang Tao，Ren Yong，Liu Xia，et al.Research on the modeling and simulation of wind turbine rotor imbalance fault［J］.Journal of Mechanical Engineering，2012，48(6):130 －135.(in Chinese)

［7］ 张钰.水介质中的转子动力学建模及模态分析研究［D］.湖北 武汉:华中科技大学，2013.

［8］ 钮冬至，樊启泰.用ANSYS软件研究轴流通风机叶轮的振动特性［J］.风机技术，2001(5):29－30.Niu Dongzhi，Fan Qitai.Research on vibration of axial fan impeller with ANSYS［J］.Fan Technology，2001(5):29 －30.(in Chinese)

［9］ 周俊杰，刘博，王定表，等.基于ANSYS的风机叶片谐响应分析［J］.中国新技术新产品，2010(16):14.Zhou Junjie，Liu Bo，Wang Dingbiao，et al.Fan blades harmonic response analysis based on ANSYS［J］.China New Technology and Products，2010(16):14.(in Chinese)

［10］ 张建，唐文献，马宝，等.某轿车白车身试验模态分析［J］.江苏科技大学学报:自然科学版，2012，26(2):146－149.Zhang Jian，Tang Wenxian，Ma Bao，et al.Experiment modal analysis of a body in white car［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2012，26(2):146 －149.(in Chinese)