樟子松枝丫材收集压缩特性模型1)

刘晋浩 于航

(北京林业大学，北京，100083) (东北林业大学)

责任编辑:张 玉。

我国林业资源丰富，开发和利用林业生物质能源具有巨大的资源禀赋优势［1］。发展林业生物质可再生资源，代替石油和天然气能源材料，是国家发展战略核心任务之一。目前面临的挑战是如何将林业生物质材料从采伐区或者城市绿化带等地经济便捷地收集及运输到应用目的地。在实际生产中，由于林业生物质堆积密度小、运输储存占用空间大、成本高，严重制约了林业生物质能的大规模应用。加快研发先进的林业生物质作业机械装备，是林业生产作业中急需解决的关键技术问题。林业生物质材料压缩特性，是设计林业生物质收集机械装备相关压缩系统的关键参数。

国内外主要针对农业纤维材料进行了压缩特性研究，学者们主要研究压缩过程中压缩力与密度、压缩力与时间等因素之间的关系［2］。意大利的Raffaele Spinelli 持续3年，针对一种车载采伐剩余物林业的工作性能及生产成本进行了全面的系统分析，确定了采伐剩余物打捆机的许多优点，并建议应该进一步研究分析降低制造和作业成本的影响因素及机理［3］。Jerry Johansson 等学者对林木压缩的优缺点做了相关的研究［4］。

本文从降低林业生物质收集和运输作业机械装备的生产成本，并根据后续应用者的要求保持林业生物质材料的物理性质出发，针对林业生物质收集作业系统机械装备低能耗、高生产率设计的要求，以东北地区主要速生材樟子松的枝丫材为试验材料，应用微机控制电子万能试验机进行闭式压缩特性试验;主要研究加载力与压缩位移、加载力与压缩密度、体积模量与压缩密度的关系;通过数理统计分析软件SPSS 建立其数学模型。旨在为林业生物质收集机械装备的压缩工作系统的动力功率选择、结构设计提供参考。

1 材料与方法

试验用枝丫材，取自黑龙江省尚志市东北林业大学帽儿山实验林场(地理坐标:N45°20'～45°25'，E127°30'～127°34')。本次试验采用平均直径为50 mm 樟子松枝丫材，含水率为47.9%。应用台式圆锯机将试验材料锯成480 mm 左右长度。

本试验在深圳新三思CMT 系列的大门式微机控制电子万能试验机上进行。试验机具有试验力、位移、速度3 种控制方式;具有自动清零、自动标定、实时显示试验数据及试验曲线、打印试验报告等功能。根据压缩试验需要，专门设计并加工了适用于大门式微机控制电子万能试验机应用的林业生物质压缩室和压缩板。林业生物质压缩室，是由45 号钢板焊接组成的长方体结构，内截面尺寸为400 mm×500 mm，压缩室高度为600 mm;在压缩室四壁开了气孔，以免压缩时装置内部空气对压缩过程造成影响。为了压缩过程的顺利进行，压缩板与压缩室内壁留有2 mm 的间隙，并在中心位置固定有与万能试验机压力传感器接触的压杆，材料为45 号钢。

首先，将20 kg 樟子松枝丫试验材料以较规则的排列形式均匀地填入压缩室，经规则摆放后，平均高度为300 mm。通过预实验中的结果分析可知，压缩速度对于压缩密度的影响比较小，所以选取常规压缩速度(30 mm/min)。应用电子万能试验机测量加载力(F)随压缩位移(l')变化的数据，另存为Excel 数据文件以进一步分析。

2 结果与分析

2.1 加载力与压缩位移的关系

通过试验获得实验材料的压缩位移自变量(l')与因变量加载力(F)的关系曲线(见图1)。由图1可见，实验材料在被压缩过程中，压缩加载力随压缩位移的增加而增长。压缩后的材料没有受到较大的破坏和变形(见图2)。

图1 加载力与压缩位移的关系

图2 压缩后取出的材料

应用数理统计分析软件SPSS，分析初始密度为333.3 kg/m3的樟子松枝丫材在压缩速度30 m/min的条件下，加载力与压缩量关系，得出两者的数学模型:F=1.065-0.057l' +0.014l'2，R2=0.999。

2.2 加载力与压缩密度的关系

根据公式ρ=m/V=m/Sl=m/(l0-l')(式中:ρ为枝丫压缩密度，m 为压缩过程中樟子松枝丫材质量，S 为压缩面积，l 为压缩过程中枝丫材料的高度，l0为枝丫材料原始高度，l'为压缩位移)，经推导与计算，得出20 kg 樟子松枝丫在加载速度30 m/min下的加载力与压缩密度关系曲线(见图3)。加载力(F)与压缩密度(ρ)的函数关系为:F =631.034-3.892ρ+0.006ρ2，R2=0.998。

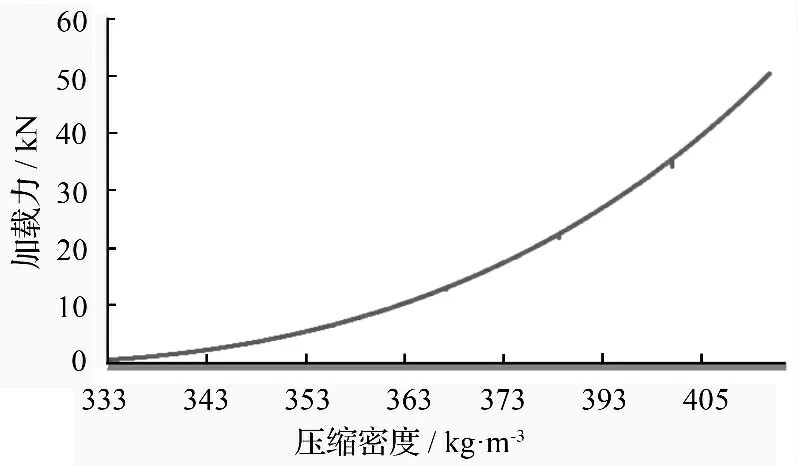
图3 加载力与压缩密度的关系

2.3 体积模量与加载力的关系

体积模量(K)，表示物料产生单位体积相对变化量时所需要的压力增量。在工程中，常用K 说明物料抵抗压缩能力的大小。K 越大，说明物料越不易被压缩，当K→∞时，表示该物绝对不可压缩;物料的种类不同，其K 也不同;同一种物料的K 随体积和压强的变化而变化［2］。英国学者Fabo rode 在研究麦秆压缩规律时，提出了用体积模量(K)来评价被压缩物质的不可压缩性［5］。本文利用樟子松枝丫材料的体积模量，说明樟子松枝丫材料在试验中的可压缩性。

体积模量:K=-dp/((dV)/V)，负号表示压强引起的体积减小。根据体积模量的定义，可以推出体积模量与压缩密度的关系。

由压缩装置p =F/S、V =Sl，所以，K =-d(F/S)/(d(Sl)/Sl)=((l0-l')/S)(dF/dl')。

通过试验测得压缩力(F)随压缩量(l')变化的规律，利用数值微分求出dF/dl'，根据数理分析软件SPSS 计算出压缩过程中樟子松枝丫材料的体积模量(K)与压缩密度(ρ)的关系(见图4)。体积模量(K)与压缩密度(ρ)的函数关系为:K=8.097×10-5ρ2-0.035ρ+2.803，R2=0.89。

4 结论

实验材料在被压缩过程中，压缩加载力随压缩位移的增加而增长。加载力与压缩位移符合以下规律:F=1.065-0.057l'+0.014l'2，R2=0.999。

实验材料在被压缩过程中，压缩密度越大，所需压力越大。加载力与压缩密度均符合以下规律:F=631.034-3.892ρ+0.006ρ2，R2=0.998。

压缩过程中，试验材料体积模量与压缩密度呈二次项关系，随着压缩密度的增加，体积模量增加，说明材料的可压缩性越来越差。K =8.097 ×10-5ρ2-0.035ρ+2.803，R2=0.89。

图4 体积模量与压缩密度的关系

从实验结果分析可知，试验中的压缩过程主要处于压缩材料之间的空隙阶段。在该实验条件下，压缩后的材料没有受到大的破坏和变形，保持了原有的物理特性，不减少后续加工中的价值损失。本文试验条件下，加载力与压缩位移、加载力与压缩密度、体积模量与压缩密度之间的数学模型，可为林业生物质采集机械装备的压缩系统动力选择和优化设计提供参考。

［1］ 谢璐琳.我国林业生物质能源产业扶持政策分析［D］.北京林业大学，2014.

［2］ 王洪波.羊草可压缩性及其应力松弛特性的虚拟样机分析研究［D］.内蒙古农业大学，2007.

［3］ Spinelli R，Magagnotti N，Picchi G.A supply chain evaluation of slash bundling under the conditions of mountain forestry［J］.Biomass and Bioenergy，2012，36(1):339-345.

［4］ Johansson Jerry，Liss Jan-Erik，Gullberg Tomas，et al.Transport and handling of forest energy bundles-advantages and problems［J］.Biomass and Bioenergy，2006，30(4):334-341.

［5］ 胡彩旗，陈夕尧，张兆玉，等.狗尾草压缩特性试验研究［J］.农机化研究，2015(3):175-178.