刚性基层对正交异性钢－混凝土组合桥面板受力性能影响

2015-03-07傅梅珍刘永健朱伟庆王成坤琚明杰

合肥工业大学学报（自然科学版） 2015年9期

关键词：钢桥关注点隔板

傅梅珍，刘永健，朱伟庆，王成坤，琚明杰

（1.长安大学公路学院，陕西西安 710064；2.东莞市公路桥梁开发建设总公司，广东东莞 523010）

0 引言

近年来，正交异性钢桥面板在大跨径桥梁中的使用逐渐增多。通过对正交异性钢桥面板使用过程持续监测发现其在使用过程中存在2个主要问题：

（1）正交异性钢桥面板局部刚度小，与沥青混凝土铺装的黏结能力差，钢桥面铺装极易破损，维修费用昂贵［1］。

（2）正交异性钢桥面板易疲劳开裂，危及全桥的安全性。

在正交异性钢桥面板表面铺设刚性基层，然后在刚性基层上加铺沥青混凝土铺装（磨耗层），即正交异性钢－混凝土组合桥面板是一种能够从根本上改善正交异性钢桥面板使用过程中存在问题的桥面板结构，其中刚性基层可采用轻质混凝土、钢纤维混凝土、活性粉末混凝土（RPC）以及超韧性混凝土（STC）等。

文献［2－3］采用轻质混凝土刚性基层，进行了钢桥复合铺装结构的大比例模型试验，并实测了该结构在不同荷位下的力学响应；文献［4］研究了一种钢桥面复合铺装结构，该结构采用了同时具有钢混抗剪连接和钢桥面板加劲作用的PBL，分析了该组合铺装结构静力性能并进行参数分析；文献［5］采用活性粉末混凝土（RPC）作为刚性基层，提出一种正交异性钢板－薄层RPC组合桥面板体系，并进行试验测试，研究结果表明，钢顶板及纵肋中应力明显降低且最大降幅超过70%；文献［6］进行大跨径和中等跨径钢桥正交异性组合桥面板体系力学行为分析与优化设计；文献［7］提出将高性能混凝土STC作为刚性基层这种钢桥面铺装新体系，并对其进行力学计算与实桥试验对比分析，结果表明该桥面体系能够降低钢桥面应力和位移，改善桥面板疲劳性能；文献［8］以广东虎门大桥为背景，利用热点应力法，分析了超高性能混凝土的轻型组合桥面板的疲劳性能。

本文依托广东某混合梁斜拉桥，采用大型有限元通用软件ANSYS，重点研究了正交异性钢－混凝土组合桥面板在车轮荷载作用下关注点应力及对应的应力集中系数，并比较分析了刚性基层厚度和弹性模量对关注点应力及应力集中系数的影响。

1 正交异性钢桥面板受力影响分析

1.1 依托工程

本文依托工程为广东某主跨138m的独塔无背索曲塔曲梁钢混混合梁斜拉桥，其跨径组合为51.5m＋138m＋55m，桥梁有限元模型如图1所示，主跨包括93m的钢箱梁段。主梁采用整幅式，标准宽度33m，荷载等级为公路Ⅰ级，钢箱梁标准长度9m，采用U型加劲肋，加劲肋间距60cm，中间设横隔板，横隔板标准间距3m，钢箱梁采用正交异性钢－薄层超韧性混凝土（STC）组合桥面结构，钢箱梁横断面及组合桥面板局部横截面分别如图2、图3所示。图2中尺寸单位为cm。

图1 桥梁有限元模型

图2 钢箱梁横断面图

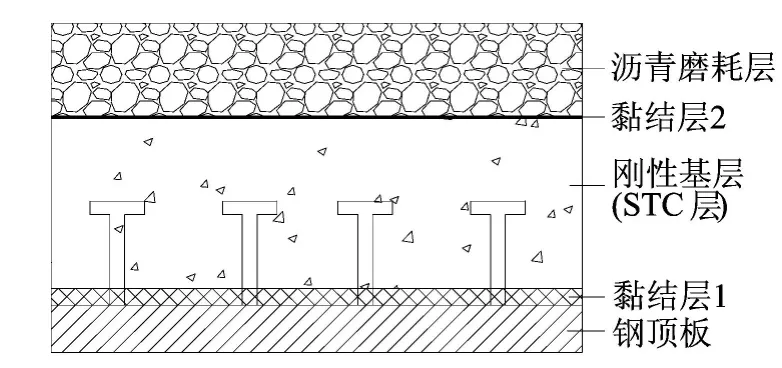
图3 组合桥面板局部横截面图

正交异性钢桥面板容易出现疲劳裂缝的地方主要包括纵肋与桥面板的连接、纵肋与横隔板的连接以及横隔板过焊孔等［9］，对应位置处的应力分别记为应力关注点① ～③。各应力关注点位置如图4所示。

图4 应力关注点位置示意图

1.2 受力分析

参照文献［10］选取加载轮压荷载，采用单轮胎轮重70kN计算，同时考虑桥面铺装层的荷载分布作用。

选取标准钢箱梁节段，横桥向选取5个U肋，宽度3m，纵桥向为4个横隔板（3跨），长度9m。边界条件采用桥面板纵向两端一端约束竖向和纵向位移，另一纵端仅约束竖向位移，横隔板底部固结，有限元模型如图5所示，有限元模型参数见表1所列。裸正交异性钢桥面板模型记为模型一，STC刚性基层的组合桥面板模型记为模型二。

图5 桥面板有限元模型

表1 有限元模型建模参数

在有限元分析中，对正交异性钢桥面板作如下假定：

（1）各部分为均匀、连续、各向同性的纯弹性材料。

（2）正交异性钢桥面板与刚性基层共节点，不考虑两者接触。

分析考虑2种加载模式，关注点①采用横隔板间中部加载，关注点②③采用横隔板处加载。

（1）关注点①。分析采用横隔板间中部施加轮压荷载，荷载作用下桥面板位移较小，模型一最大竖向位移为0.61mm，模型二最大竖向位移为0.32mm，如图6所示，模型二较模型一位移降低47.5%，模型二桥面板刚度明显提高。

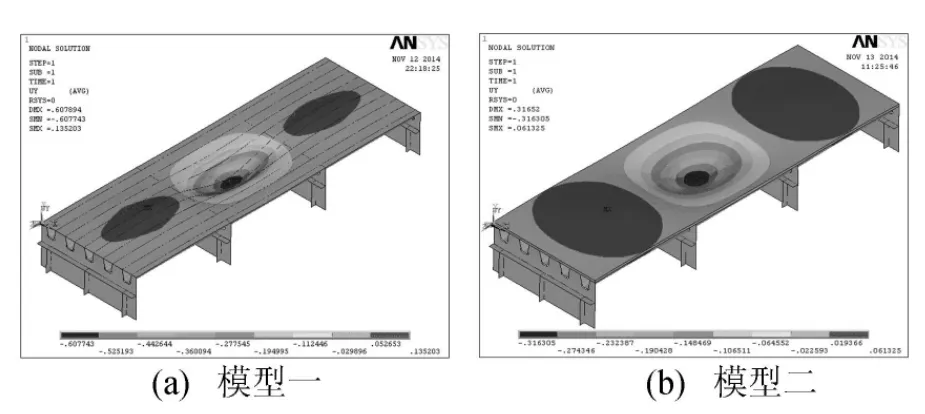
图6 横隔板间加载时桥面板位移云图

桥面板应力极值出现在纵肋底部，如图7所示。模型一应力极值为32.76MPa，关注点①应力极值为20.18MPa；模型二应力极值较模型一小，为21.08MPa，关注点①处应力极值为7.58MPa，对应的刚性基层最大拉应力为2.97MPa，出现在刚性基层顶部。模型二关注点①处应力约为模型一对应位置应力的1／3～1／4，降幅约为70%。

图7 桥面板应力云图

（2）关注点②③。分析采用横隔板处施加轮压荷载，荷载作用下模型一最大竖向位移为0.094mm，模型二最大竖向位移为0.04mm，如图8所示。模型二较模型一位移降低约57%，模型二桥面板刚度明显提高。

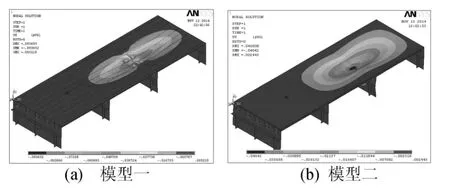
图8 横隔板处加载时桥面板位移云图

桥面板应力极值出现在横隔板过焊孔处，即应力关注点③处，如图9所示。模型一应力极值为34.73MPa，应力关注点②处应力为17.80MPa，关注点③处应力极值为34.73MPa，如图10a所示；模型二应力极值较模型一小，为27.48MPa，应力关注点②处应力较小，为3.17MPa，关注点③应力为27.48MPa，如图10b所示，对应的STC层极值拉应力为1.30MPa，出现在刚性基层顶部。模型二关注点②处应力约为模型一对应位置应力的1／6～1／5，降幅约82%；模型二关注点③处应力较模型一降幅约为21%，降幅较其他2个关注点小。

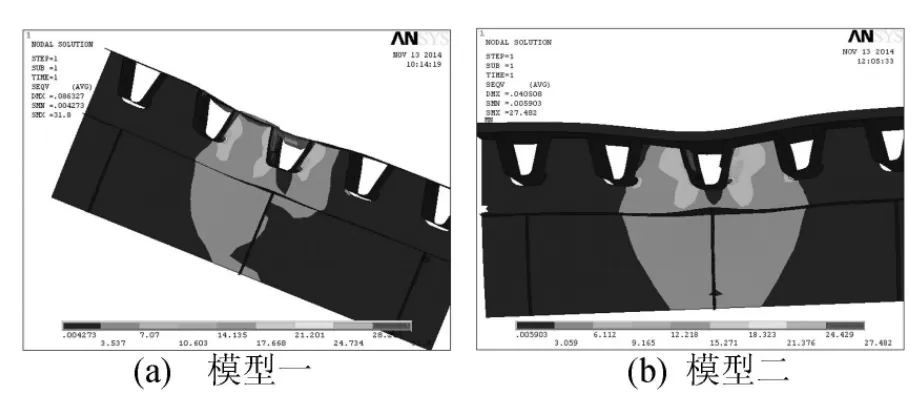
图9 横隔板处加载时桥面板应力云图

由上述分析可知，采用横隔板间中部加载和横隔板处加载，模型二的最大挠度较模型一最大挠度分别下降47.5%和57%，模型二桥面板刚度明显提高，即铺设刚性基层后的组合桥面板刚度明显提高。模型二各应力关注点处应力均较模型一对应位置处应力降低且关注点③降幅较其他2个关注点小。

2 关注点应力集中系数影响分析

2.1 子模型法

子模型法就是将子模型从整个较粗糙的整体模型中分割出来，把整体模型在切割边界的计算位移值作为子模型的边界条件，因此子模型法又称切割边界位移法或特定边界位移法。采用子模型技术进行分析能求得模型关注部位精确解且能提高计算效率。

基于以上思路以及ANSYS软件，子模型法建模计算流程如图11所示。

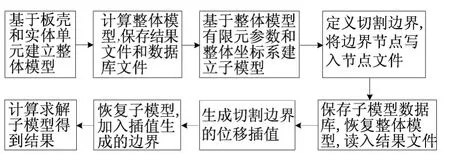
图11 子模型计算流程

2.2 应力集中系数

应力集中系数η为热点应力与名义应力的比值。名义应力指远离焊缝区域的应力，根据国际焊接学会规范IIW［11］的推荐，可取距离焊趾1.5t（t为板厚）处的应力σ1.5t作为名义应力。热点应力指最可能发生疲劳裂纹的起始点处的应力，可通过外推法计算，如图12所示［12－13］。

图12 外推计算示意图

IIW推荐的外推法分为两点线性外推和三点2次外推，本文采用两点线性外推。该法提取距离热点0.4t和1.0t处结构应力值，进行2点线性外推，计算公式为：

其中，σhs为热点应力；σ0.4t为距焊趾0.4t处的应力；σ1.0t为距焊趾1.0t处的应力。

应力集中系数η计算公式为：

2.3 刚性基层对关注点应力集中系数影响分析

采用子模型法建立子模型，模型边界采取内力和位移内插从原始模型中提取，关注点①②③计算模型及边界条件分别如图13～图15所示。

图13 关注点①模型及边界

图14 关注点②模型及边界

图15 关注点③模型及边界

采用两点线性外推法计算关注点处焊缝热点应力。关注点①模型一：提取顶板上距离热点（焊趾）0.4t和 1.0t处应力，即σ0.4t＝17.07MPa，σ1.0t＝13.49MPa，带入（1）式得热点应力σhs＝19.47MPa。名义应力为σ1.5t＝11.52MPa，则应力集中系数η＝σhs／σ1.5t＝1.69。同理提取其他关注点外推点处应力、名义应力、热点应力并计算应力集中系数，见表2所列。

由表2可知，设置刚性基层能降低各关注点处结构应力，且关注点①②处应力集中系数也降低，但是关注点③处应力集中系数提高。

表2 各关注点处应力及应力集中系数

3 参数分析

3.1 刚性基层厚度影响分析

3.1.1 对关注点应力的影响分析

以关注点①为例分析刚性基层厚度对组合桥面板关注点应力的影响，轮压荷载施加位置为横隔板间中部。刚性基层材料选取STC（弹性模量40GPa，抗拉强度25MPa），轮压荷载下组合桥面板应力极值、应力关注点①③处应力和刚性基层应力如图16所示。

组合桥面板各应力均随刚性基层厚度的增加而减小，且当刚性基层厚度较小（＜165mm）时，应力极值出现在纵肋底板部位，当刚性基层厚度达到165mm时，应力极值向横隔板过焊孔转移，即向应力关注点③转移。

图16 组合桥面板各应力随刚性基层厚度的变化

3.1.2 对关注点应力集中系数的影响分析

分别选取刚性基层厚度为40、50、60、70、80mm 5组参数进行刚性基层厚度对关注点应力集中系数影响分析，计算结果见表3所列。关注点应力集中系数随刚性基层厚度增加而增大。

刚性基层厚度对关注点应力及应力集中均有显著的影响，刚性基层厚度越大，关注点应力值降低，但是应力集中越明显，即应力集中系数越大。

表3 不同厚度下关注点①应力集中系数计算结果

刚性基层厚度增加能够提高组合桥面板刚度，降低组合桥面板应力，但是会增加应力关注点应力集中程度，降低桥面板疲劳性能，实际工程要兼顾组合桥面板静力及疲劳性能综合选取。

3.2 刚性基层弹性模量影响分析

采用3.1节相同的方法，假设刚性基层厚度为100mm，分别选取刚性基层弹性模量为30.0、32.5、34.5、36.0、40.0GPa 5组参数进行刚性基层弹性模量对关注点应力及应力集中系数影响分析。

3.2.1 对关注点应力的影响分析

刚性基层弹性模量对关注点应力影响分析计算结果见表4所列。

表4 刚性基层弹性模量对关注点应力的影响 MPa

由表4可知，刚性基层弹性模量增加能降低组合桥面板极值应力及关注点应力，但是刚性基层自身应力会增加。

3.2.2 对关注点应力集中系数的影响分析

刚性基层弹性模量对关注点①应力集中系数影响分析的计算结果见表5所列。

由表5可知，刚性基层弹性模量增加，应力集中系数降低。因此，降低关注点应力集中现象，采用弹模较高的高韧性刚性基层能改善桥面板疲劳性能。

刚性基层弹性模量增加能够同时降低组合桥面板关注点应力及应力集中系数，但是会提高刚性基层自身应力，实际工程中建议采用高弹模且抗拉强度高的高韧性混凝土刚性基层。

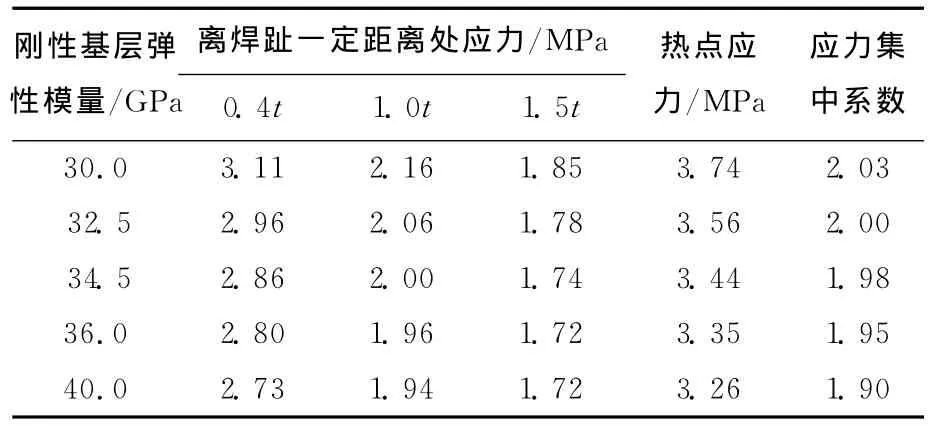
表5 不同模量下关注点①应力集中系数计算结果

4 结论

本文采用大型有限元通用软件ANSYN，重点研究正交异性钢－混凝土组合桥面板在车轮荷载作用下关注点应力及对应的应力集中系数，比较分析了刚性基层厚度和弹性模量对关注点应力及应力集中系数的影响，得到如下结论：

（1）与裸正交异性钢桥面板相比，铺设刚性基层后的组合桥面板刚度明显提高，不同加载位置下对应最大竖向位移降低45%～60%；应力关注点应力极值也降低，其中关注点①处应力约为裸正交异性钢桥面板对应位置应力的1／3～1／4，降幅约为70%；关注点②处应力约为裸正交异性钢桥面板对应位置应力的1／6～1／5，降幅约82%；关注点③处应力极值降幅约21%，降幅较其他2个关注点小。

（2）设置刚性基层能降低关注点①②处应力集中系数，但是关注点③处应力集中系数提高。

（3）刚性基层厚度增加，关注点应力值降低，但是应力集中系数增大，实际工程要兼顾组合桥面板静力及疲劳性能综合选取刚性基层厚度。

（4）刚性基层弹性模量增加能降低组合桥面板极值应力及关注点应力，降低关注点应力集中参数，但刚性基层自身应力增加，实际工程中建议采用高弹模且抗拉强度高的高韧性混凝土刚性基层。

［1］黄卫.大跨径桥梁钢桥面铺装设计理论与方法［M］.北京：中国建筑工业出版社，2006：12－25.

［2］朱铭.钢－轻质混凝土组合桥面及铺装结构试验研究［D］.西安：长安大学，2011.

［3］张久鹏，刘少文，刘永健.钢桥面复合铺装结构的大比例模型试验［J］.同济大学学报：自然科学版，2013，41（12）：1837－1842.

［4］姚文奇.基于PBL连接件的钢桥面复合铺装结构静力性能分析［D］.西安：长安大学，2012.

［5］邵旭东，曹君辉，易笃韬，等.正交异性钢板－薄层RPC组合桥面基本性能研究［J］.中国公路学报，2012，25（2）：40－45.

［6］耿东升.正交异性组合桥面体系力学行为分析与优化设计［D］.西安：长安大学，2013.

［7］李嘉，冯啸天，邵旭东.STC钢桥面铺装新体系的力学计算与实桥试验对比分析［J］.中国公路学报，2014，27（3）：39－44.

［8］丁楠，邵旭东.轻型组合桥面板的疲劳性能研究［J］.土木工程学报，2015，48（1）：74－81.

［9］王春生，付炳宁，张芹，等.正交异性钢桥面板足尺疲劳试验［J］.中国公路学报，2013，26（2）：69－75.