基于电子齿轮箱的蜗杆砂轮磨齿机几何误差补偿解耦研究

韩 江， 张魁榜， 杨清艳， 夏 链

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

齿轮是机械产品的重要基础件，应用非常广泛，磨齿是实现齿轮精加工的有效方法，而在磨齿加工中蜗杆砂轮磨齿是一种高精度、高效率的磨削方法，可以减小齿形误差、实现齿廓修形、提高齿轮承载能力、降低传动噪音，是小模数、大批量齿轮精加工的最佳选择［1］。但机床影响各项精度的因素比较复杂，它的精度指标是影响工件加工精度的重要因素。提高机床精度和减小加工误差的主要途径是提高机床的机械性能、实时对机床空间误差进行补偿［2－5］。

本文利用多体系统理论并考虑数控蜗杆砂轮磨齿机的运动特点，建立了机床空间几何误差模型并进行误差补偿解耦，解出的各轴运动误差补偿量可以为蜗杆砂轮磨齿机的实时误差补偿提供理论基础。

1 数控蜗杆砂轮磨齿机加工原理

数控蜗杆砂轮磨齿机数控系统柔性电子齿轮箱［6－7］采用主从式电子齿轮箱结构，并在自主开发的系列齿轮数控系统中得以实现，其原理图如图1所示。通过编码器将主轴电机运动信息反馈到微处理器DSP，根据齿轮加工联动数学模型，电子齿轮箱插补模块实时计算其他各运动伺服轴位置和速度参数，完成齿轮加工所需的联动关系，从而实现各种不同类型的齿轮加工。

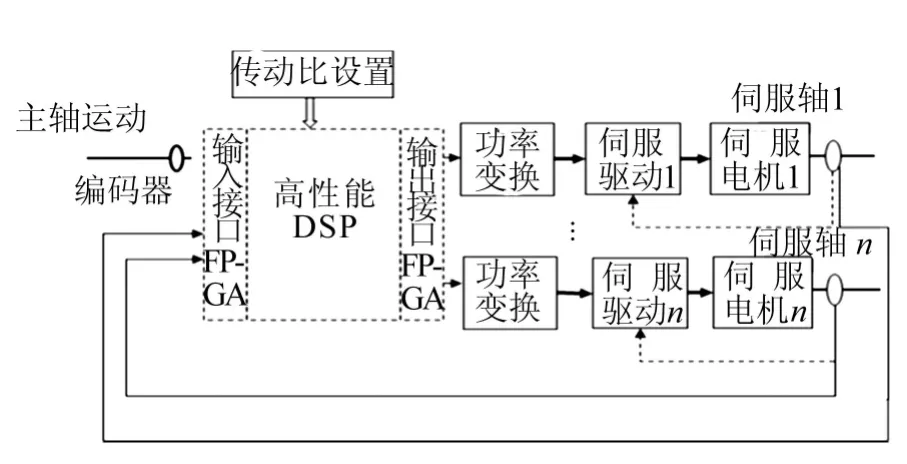
图1 电子齿轮箱原理示意图

齿轮加工机床如图2所示，运动轴有：砂轮的转动B轴（切削运动）、齿坯的转动C轴（分齿运动）、砂轮沿工件轴向的走刀运动Z轴、砂轮沿工件径向的走刀运动X轴、切向走刀运动Y轴和砂轮角度调整轴A轴。

图2 蜗杆砂轮磨齿机床结构

蜗杆砂轮磨齿加工时各轴联动关系为：

其中，nB、nC分别为砂轮转速和工件转速，单位为r／min；vY、vZ分别为Y轴、Z轴的移动速度，单位为 mm／min；k为砂轮头数；z0为工件齿数；β、λ分别为斜齿轮螺旋角和刀具的安装角；mn为齿轮的法面模数；kZ、kY为系数常量。当采用往复多次磨削加工工艺时，Y轴没有进给运动；在深切缓进磨削加工时需要进行Y轴方向窜刀运动。采用“差动法”加工斜齿轮或深切缓进加工方法磨齿时，机床工件主轴与机床砂轮主轴之间不仅要实现严格的展成分齿运动，还要完成与Z轴、Y轴或Z轴和Y轴进给有关的附加合成运动。

2 蜗杆砂轮磨齿机空间误差模型分析

由于制造、安装等方面存在的误差，一构件相对另一构件运动后会偏离理想位置，产生误差。磨齿加工时，每一刀刃在回转中的切削是从切入齿坯到切出齿坯，刀刃上任一点的回转平面与齿面呈λ角，砂轮刀刃磨削过程中齿坯始终在连续转动，因此，磨齿过程是一个刀刃周而复始的切削运动，形成接近渐开线的折线段。加工过程中的误差都是通过刀具的切削刃廓形及刀具与工件之间的相对运动传递到工件上，因此可以建立数学模型真实地反映磨齿过程，得出磨齿机空间误差。

根据机床运动副误差运动学原理［8－9］和多体系统理论［10－12］，建立蜗杆砂轮磨齿机各运动副间的变换矩阵。蜗杆砂轮磨齿机在加工过程中起主要作用的有3个移动轴X、Y、Z和3个旋转轴A、B、C，建立蜗杆砂轮磨齿机床的坐标系，如图3所示。基坐标系S1（O1X1Y1Z1）固连于床身，坐标系S2（O2X2Y2Z2）固联于砂轮进刀架X轴，S3（O3X3Y3Z3）固 联 于 砂 轮 架 进 刀Z轴，S4（O4X4Y4Z4）固 联 于 砂 轮 架 进 刀Y轴，S5（O5X5Y5Z5）固 联 于 砂 轮 架 旋 转A轴，S6（O6－X6Y6Z6）固 联 于 砂 轮 旋 转B轴，St（Ot－XtYtZt）是砂轮边缘点坐标系，S7（O7X7Y7Z7）固联于工件旋转C轴，Sp（OpXpYpZp）是工件边缘点坐标系。

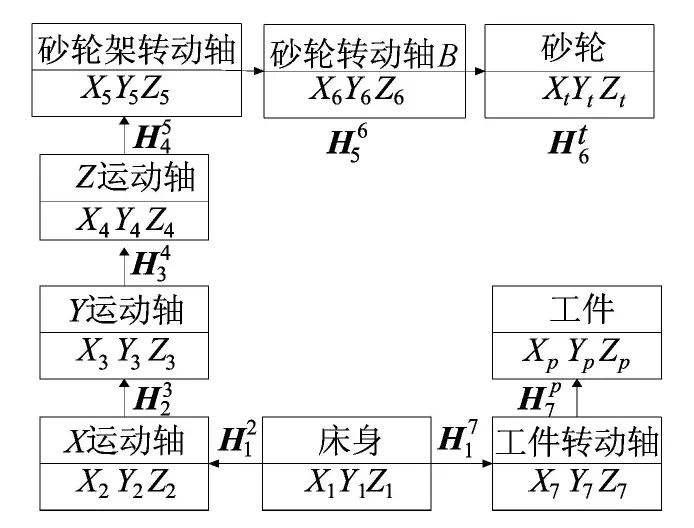
图3 蜗杆砂轮磨齿机床的坐标系

2.1 理想状态下各运动副的坐标齐次变换矩阵

（1）移动副坐标齐次变换矩阵。当机床的砂轮架进刀X轴、砂轮架走刀轴Z轴移动无误差时，相邻体之间的齐次变换矩阵为：

（2）转动副坐标齐次变换矩阵。当A、B、C轴无旋转误差时，其相邻体之间变换矩阵为：

其中，φ为A轴绕其X5轴的转角；α为B轴绕其Z6轴的转角；β为C轴绕其Y7轴的转角；D为砂轮外径为砂轮边缘上点坐标系t相对于砂轮旋转B轴的齐次坐标变换。

在理想（无误差）情况下，砂轮边缘上点坐标系t和工件坐标系p在空间重合，因此砂轮边缘上点坐标系t相对于机床底座基坐标系的齐次坐标变换，等于坐标系p相对于机床底座基坐标系的齐次坐标变换，即

根据多体系统理论并结合图2磨齿机的结构，可以分别得到：

可以得出工件C轴坐标系S7相对于工件坐标系p的齐次变换矩阵为：

显然，在无误差情况下，砂轮边缘上点坐标系t相对于工件坐标系p的齐次变换矩阵为：

其中，I为单位矩阵。

2.2 考虑误差时各运动副坐标齐次变换矩阵

在机床的加工过程中，如果各种误差为0，则砂轮边缘上点的空间坐标系t与工件的空间坐标系p是重合的；但实际中，由于各种误差的存在，砂轮边缘上点的空间坐标与工件的空间坐标将发生分离，此时砂轮边缘上点与工件之间的坐标变换矩阵即所求的误差模型矩阵。

根据机床多体系统理论，对于数控蜗杆砂轮磨齿机加工过程中的3个移动轴X、Y、Z和3个旋转轴A、B、C，总共包括39项空间误差。

在有误差的情况下，t与p在空间上产生了分离，t相对p的齐次变换矩阵即为误差矩阵，也就是所求的误差模型为：

把（12）式代入（13）式中，得到所要求的误差模型，基于小误差假设综合误差矩阵为：

其中，ΔξX、ΔξY、ΔξZ为平移误差；ΔφX、ΔφY、ΔφZ为转角误差。将（12）式展开并舍去二次及二次以上的分量，再结合（14）式得到该磨齿机的3个位置及3个转角的综合误差模型。以上所有的误差都将转化到砂轮刀具上来，在加工过程中最终将砂轮的位置偏差转化到工件上来。

3 基于电子齿轮箱的几何误差补偿解耦

为了对综合误差进行补偿，文献［13］提出了根据综合误差进行解耦获得各运动副的位置或方向误差补偿运动量，必须通过各运动副关节的微分运动来加以补偿（补偿运动中不考虑误差运动）。补偿运动为误差运动的逆运动，其目标为实施补偿后使分离的刀尖坐标系t和工件坐标系p在空间重合，即＝I，其中为砂轮边缘上点坐标系t相对于工件坐标系p的补偿运动变换矩阵，左上标c表示补偿运动。

以上的理论对一般的各个独立运动轴是适合的，但对于蜗杆砂轮磨齿机这样的各个轴运动有比例关系的，误差解耦应该再考虑各轴的联动关系，进一步解耦，使加工误差最小。

3.1 各轴的误差补偿量初步解耦计算

在进行加工过程中，砂轮主轴B是电子齿轮箱插补主动轴，其他轴跟随B轴按照一定的联动关系进行运动，因此对于蜗杆砂轮磨齿机在加工过程中能够进行补偿的有X、Y、Z、A、C轴。基于小误差补偿假设，根据机器人运动学的微分变换原理可得刀尖坐标系t相对于工件坐标系p的变换微分为：

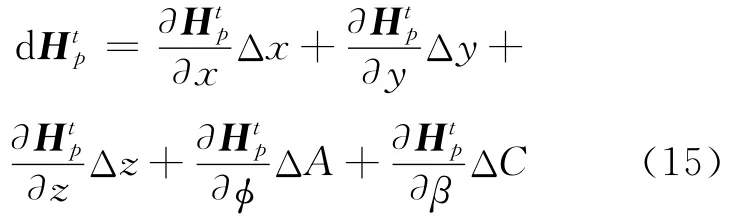
其中，Δx、Δy、Δz、ΔA、ΔC分别为X、Y、Z、A、C轴运动副及转动副的补偿微分运动量，且有：

根据相关的变换矩阵、逆变换矩阵，可以得出d关于 Δx、Δy、Δz、ΔA、ΔC的矩阵表达式即（17）式，其计算过程参见文献［10］。

其中，h1、h2、h3计算公式如下：

基于小误差补偿运动，砂轮边缘上点坐标系t相对于工件坐标系p的齐次坐标变换矩阵即误差补偿运动矩阵，可用齐次变换矩阵描述，即

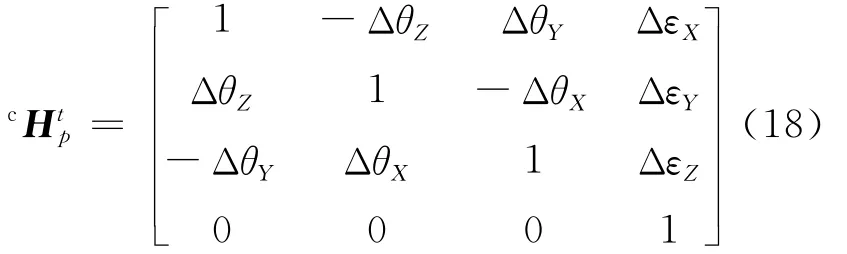
其中，ΔθX、ΔθY、ΔθZ为方向补偿量；ΔεX、ΔεY、ΔεZ为位置补偿量。且有：

可以由（17）式和（19）式解出关于 Δx、Δy、Δz、Δβ、Δα、Δφ的表达式。

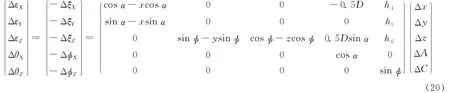
其中，h4＝－zcosα－xcosα－0.5Dcosα－0.5D；h5＝－zsinα－xsinα－0.5Dsinφ－

ΔξX、ΔξY、ΔξZ，ΔφX、ΔφZ可由误差矩阵的齐次坐标表示，也是机床X、Y、Z、A、C轴运动误差补偿量，但该方程没有解。对于蜗杆砂轮磨齿机，必须考虑其电子齿轮箱耦合运动的特殊性。

3.2 基于电子齿轮箱的各轴误差补偿解耦计算

蜗杆砂轮磨齿机在采用深切缓进磨削时，各轴运动关系如（1）式，在联动展成运动过程中，主轴B是基准轴，仅进行速度控制，不进行位置控制，无法进行误差补偿，因此可以进行补偿的轴有Z轴、Y轴、A轴和C轴。

在电子齿轮箱插补进行之前调整好A轴，它不参加联动展成关系，因此在调整过程中对其误差进行补偿即可。在联动插补过程中，只需对Z轴、Y轴和C轴进行补偿。

对（1）式进行微分变形得：

其中，B轴补偿量为0，整理得：

联立（20）式和（22）式，求出X、Y、Z、A、C各轴的误差补偿值，即得出关于蜗杆砂轮磨齿机的几何误差解耦补偿量，其解如下：

4 误差补偿实验研究

自主开发的HFUT－GSK系列蜗杆砂轮磨齿加工数控系统平台如图4所示。

在此平台上进行误差补偿实验研究，电机采用Panasonic MINAS A5系列，具体型号为MADHT1505。数控系统插补周期为1ms，直线轴分辨率为10－4mm，旋转轴分辨率为0.000 1°。

工件与刀具具体参数见表1所列，工件是标准的渐开线圆柱齿轮，刀具是标准的蜗杆砂轮，采用多次磨削法进行加工，不需要Y轴参与联动。

表1 工件与刀具参数

对电机施加稳定载荷，以达到与机床实际加工运行相接近的状况，通过测试代码，获取数控系统编程位置，与电机实际编码器反馈器相比较，从而获得位置误差，测试部分代码如下：

G81开启电子齿轮箱后，Y、Z、B、C轴通过电子展成形成齿轮加工，测试X、Z轴进给，每次进给10mm，共进给100mm，数控系统每隔30ms从编码器读取反馈位置，自动计算编程位置与实际电机位置差值，获取实时误差信息。获取位置误差后，在自主研发的数控系统内核中开发误差补偿功能模块，进行齿轮加工误差补偿，误差补偿效果如图5所示。

由图5a可知，X轴补偿前最大误差为0.012mm，补偿后为0.001 2mm；Z轴补偿前最大误差为0.008mm，补偿后为0.001mm。

根据联动关系，C轴跟随Y、Z、B轴运动，因此存在较大波动，从图5b中可以看出，补偿前C轴平均误差约为0.03mm，补偿后平均误差约为0.004mm。

因此根据误差解耦补偿公式，可以获得很好的误差补偿效果。

5 结束语

为了提高蜗杆砂轮加工齿面精度，本文先对蜗杆砂轮磨齿加工原理进行了详细的分析，利用齐次坐标变换理论建立了符合实际加工的蜗杆砂轮磨齿机几何误差数学模型。结合蜗杆砂轮磨齿机运动联动关系，在一般解耦方法的基础上，进行基于电子齿轮箱的各轴联动误差耦合的解耦算法研究；在自主开发的数控系统平台上进行误差补偿实验，获得了良好的补偿效果，验证了蜗杆砂轮磨齿加工几何误差补偿解耦算法的正确性。

［1］ Karpuschewski B，Knoche H J，Hipke M.Gear finishing by abrasive processes［J］.CIRP Annals：Manufacturing Technology，2008，57（2）：621－640.

［2］ Ni J，Wu S M.An on－line measurement technique for machine volumetric error compensation［J］.Journal of Manufacturing Science and Engineering，1993，115（1）：85－92.

［3］ 杨清艳，韩 江，张魁榜，等.数控成形砂轮磨齿机床几何误差分析与函数补偿法［J］.中国机械工程，2013，24（23）：3144－3149.

［4］ Okafor A C，Ertekin Y M.Derivation of machine tools error models and error compensation procedure for three axes vertical machining center using rigid body kinematics［J］.International Journal of Machine Tools and Manufacture，2000，40（8）：1199－1213.

［5］ 夏 链，谢 捷，许少平，等.Mikron UCP 800数控机床的定位精度检测与误差补偿［J］.合肥工业大学学报：自然科学版，2008，31（6）：835－838.

［6］ 韩 江，夏 链，田晓青.一种高速高精度柔性电子齿轮箱的控制方法：中国，CN201310180873.0［P］.2013－10－18.

［7］ 夏 链，程 杰，韩 江，等.基于DSP6713插补控制方法的研究及应用［J］.机床与液压，2013，41（15）：111－115.

［8］ Srivastava A K，Veldhuis S C，Elbestawit M A.Modeling geometric and thermal errors in a five－axis CNC machine tool［J］.International Journal of Machine Tool and Manufacture，1995，35（9）：1321－1337.

［9］ Lei W T，Hsu Y Y.Accuracy enhancement of five－axis CNC machines through real－time error compensation［J］.International Journal of Machine Tool and Manufacture，2003，43（9）：871－877.

［10］ Shabana A A.Transient analysis of flexible multi－body systems，partⅠ：dynamics of flexible bodies［J］.Computer Methods in Applied Mechanics and Engineering，1986，54（1）：75－91.

［11］ Agrawal O P，Saigal S.Dynamic analysis of multi－body systems using tangent coordinates［J］.Computers and Structures，1989，31（3）：349－355.

［12］ Boutaghou Z E，Erdman A G.On various non－linear rod theories for the dynamic analysis of multi－body systems，partⅠ：formulations［J］.Journal of Sound and Vibration，1993，164（2）：207－223.

［13］ 任永强，杨建国.五轴数控机床综合误差补偿解耦研究［J］.机械工程学报，2004，40（2）：55－59.