基于ANSYS的曲轴圆角滚压特性分析
2015-03-07杨秀芝肖新华杨春杰
杨秀芝, 张 锐, 王 健, 肖新华, 杨春杰
(1.湖北理工学院 机电工程学院,湖北 黄石 435000;2.武汉理工大学 自动化学院,湖北 武汉 430000;3.武汉理工大学 机电工程学院,湖北 武汉 430000)
0 引 言
曲轴作为发动机的主要零件之一,在工作过程中承受较大的弯曲应力和扭转应力,很容易疲劳断裂。大量的理论分析和实践表明,疲劳破坏主要集中产生在连杆颈、主轴颈和曲柄连接的过渡圆角处,因此有必要对曲轴圆角部位采取一定的强化措施以提高曲轴的使用寿命。强化措施中最好的方法是圆角滚压强化,该方法的强化效果主要取决于滚压力、滚压圈数、曲轴材料强度和变形能力[1-2]。
目前国内外对曲轴圆角滚压的工艺研究并不系统,而采用试验方法选取合适的滚压参数不仅时间长、成本高,且难于操作。本文采用有限元仿真分析的方法,不仅有助于快捷地获取滚压后圆角内部应力和应变分布规律,而且可以帮助选取合适的滚压参数,有效地降低了制造和测试成本,具有较大的工程应用价值。
1 曲轴滚压数学模型的建立
滚压层深度a和滚压力P的关系如下:

其中,m=1+0.07R,1/R=1/R1+1/R2+1/R3+1/R4,R1为滚轮半径,R2为连杆轴颈圆角半径,R3为主轴颈圆角半径,R4为相关轴颈半径;σs为曲轴材质屈服强度。
根据等效空间应力理论,在滚压时滚轮和圆角的接触半宽度从0开始不断扩展到最大宽度,其余各点的接触宽度向两侧对称缩小。加载后等效接触线扩展为长半轴为r(圆弧半径)、短半轴为b(最大负荷点的接触半宽度)的椭圆等效接触面,如图1所示。
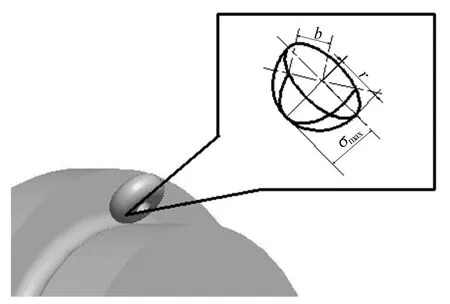
图1 曲轴滚压部位应力分布示意图
考虑滚压加工中的塑性变形,可得:

其中,σmax为滚压后最大应力;P为滚轮上总负荷;r为圆弧半径;b为最大负荷点接触半宽度;ks为塑性系数,与载荷力大小及曲轴材料特性、工作环境等有关[3]。
滚压塑性变形时全量应变与应力之间的关系与弹性应变时完全不同。塑性变形可以认为体积不变,应力和应变之间的关系是非线性关系,与加载里程和材料应变路线相关。
2 曲轴滚压仿真模型的建立
2.1 曲轴滚压简化模型的建立
在三维造型软件中建立曲轴和滚压轮三维模型,其中曲轴圆角半径为1.8mm,滚轮张开角为45°,滚压轮半径为 4.8mm,曲轴轴颈半径为23.95mm。简化数学模型后将三维模型导入到ANSYS/Workbench中,分别添加曲轴和滚压轮材料。本仿真属于三维刚柔接触瞬态仿真分析,滚压轮采用刚体设置,曲轴采用变形体设置、双线性等向强化模型,弹性模量为114GPa,泊松比为0.23,屈 服 极 限 为 480MPa,切 向 模 量 为11.25GPa,密度为7 830kg/mm3。仿真模型中滚压轮为刚体,故将其刚度加大为普通值的100倍[4];划分曲轴主体网格时应尽可能粗化网格,而为了提高求解精度,在接触副处应细化网格,将滚压轮和曲轴圆角处的网格大小设置为0.8mm,如图2所示。

图2 曲轴滚压有限元模型
2.2 边界条件
对曲轴端面施加Joints约束,类型选择为Revolute,约束除围绕轴颈自身轴线转动的自由度外的全部自由度。同样在滚压轮中心的圆柱孔上施加Joints约束,设置为Translational类型,约束除图中X方向外的所有自由度(X方向刚好指向曲轴圆角方向),如图3所示。

图3 滚压轮约束设置
实际滚压中需考虑滚压接触处摩擦力,为了简化仿真模型、方便收敛,在滚压轮表面和曲轴圆角处建立无摩擦接触对。实际生产中曲轴转速一般为30~60r/min[5],为了提高滚压效率,将曲轴上围绕自身轴线转动的速度设置为60r/min。在滚压轮上施加沿X方向的滚压力,滚压力加载模式如图4所示。
根据文献[5-8]所述,滚压中圈数以8~10圈为宜,故在仿真模型中设置滚压进给圈数为2圈,保持圈为6圈,退出圈为2圈(总圈数为10圈),进行求解。
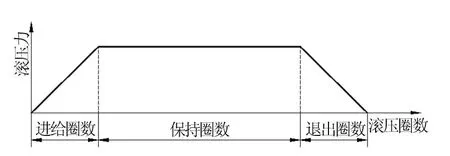
图4 滚压力加载模式
2.3 求解并提取数据
加载不同滚压力进行仿真求解,并提取圆角部位的应力和应变数值进行分析。为了便于分析对比圆角内侧和周向的应力应变,分别以圆角圆心和轴颈圆心为坐标原点,在圆角部位以X轴为极轴建立极坐标系,如图5所示。

图5 圆角和圆角周向坐标图
3 不同滚压力下应力和应变分布
3.1 圆角深度方向的应力和应变分布
仿真后,提取滚压力为13kN时57.5°位置圆角深度方向应力和塑性应变结果,如图6所示。不同滚压力下获得的57.5°位置圆角深度方向应力和塑性应变关系如图7所示。

图6 13kN时曲轴深度方向应力和应变分布

图7 不同滚压力下深度方向应力和塑性应变分布
由图7可知,任意滚压力下,最大压缩应力和塑性应变出现在曲轴圆角和滚压轮接触处(即圆角表面),应力和应变随着深度急剧下降,深度超过4mm后的应力和塑性应变可以忽略不计。同时滚压力越大,曲轴圆角深度方向4mm范围内的压缩应力和塑性应变也快速增大,但深度超过4mm后应力和应变基本没有明显区别。
3.2 圆角内侧应力和应变分布
由于曲轴圆角在滚压后还应进行磨削,磨削量一般为0.2~0.4mm,所以提取圆角内侧深度为0.4mm处的应力和应变值。滚压力为13kN时圆角内侧深度为0.4mm处应力和塑性应变分布,如图8所示。不同滚压力下圆角内侧应力和应变关系如图9所示。
由图9可知,压缩应力和塑性应变主要集中在20°~90°范围内,最大塑性应变出现在65°附近,圆角两侧由于受滚压轮挤压较少,所以应力和应变都较小,并且没有产生文献[1]中所说的对曲轴疲劳强度不利的轴向拉应力,说明滚压效果较好;同时滚压力越大,压缩应力和塑性应变也越大,说明合适的滚压力可以有效地提高滚压效果。
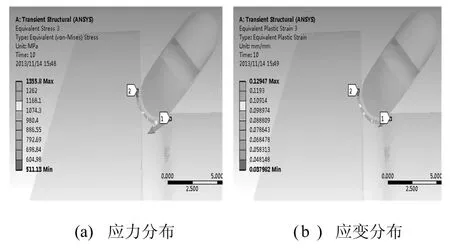
图8 13kN时曲轴圆角内侧应力和应变分布

图9 圆角内侧0.4mm处应力和塑性应变分布
3.3 圆角周向应力和应变分布
滚压力为13kN时圆角内部深度为0.4mm处,周向应力和应变分布图如图10所示。不同滚压力下的圆角深度0.4mm处周向应力和塑性应变关系如图11所示。

图10 13kN时曲轴圆角周向应力和应变分布

图11 圆角内侧0.4mm处周向应力和应变分布
根据仿真结果可以看出,经过不同滚压力滚压后,整个圆角内部区域都受到有效压缩应力,产生了一定的塑性应变,并且整个圆角的塑性应变都是比较均匀的,说明该滚压是合理可靠的。同时滚压力越大,产生的压缩应力和塑性应变也明显增大。
4 结束语
本文运用有限元分析方法,通过建立曲轴圆角滚压仿真模型,获得了曲轴圆角在滚压后的应力和应变分布规律;同时发现曲轴圆角经过滚压后,圆角所产生的压缩应力和塑性应变主要发生在距离圆角表面4mm、圆角中间区域20°~90°的范围内,并且经过滚压后圆角周向范围内都产生了较为均匀的压缩应力和塑性应变。通过对比不同滚压力下圆角处产生的应力和应变,发现合理增大滚压力可以有效增大滚压层塑性应变和压应力,从而提高滚压质量和效率,为实际曲轴加工和测试提供了参考。
[1] 赵红兵,郭晨海,梁福祥.曲轴圆角滚压残余应力的分布研究[J].小型内燃机与摩托车,2012,41(2):33-36.
[2] 陈立东,马淑英,刘荣昌,等.曲轴滚压强化机液压系统的设计[J].机床与液压,2009,37(7):66-68.
[3] 刘荣昌,薛隆泉,王慧武,等.曲轴圆角滚压强化加载范围与原则的研究[J].农业机械学报,2005,36(2):119-122.
[4] 张 锐,胡荣强,王培懿,等.曲轴圆角滚压有限元分析[J].热加工工艺,2009,38(19):101-104.
[5] 李海国,李满良.曲轴圆角滚压强化工艺综述[J].山东农机,2002(2):16-20.
[6] Spiteri P,Ho S,Lee Y L.Assessment of bending fatigue limit for crankshaft sections with inclusion of residual stresses[J].International Journal of Fatigue,2007,29(2):318-329.
[7] Gardin C,Courtin S,Bézine G,et al.Numerical simulation of fatigue crack propagation in compressive residual stress fields of notched round bars[J].Fatigue and Fracture of Engineering Materials and Structures,2007,30(3):231-242.
[8] Choi K S,Pan J.Simulations of stress distributions in crankshaft sections under fillet rolling and bending fatigue tests[J].International Journal of Fatigue,2009,31(3):554-557.
