表贴式永磁电机阶梯形永磁体设计及特性分析

王海星， 李志义， 封海潮

（1.河南理工大学 电气工程与自动化学院，河南 焦作 454003；2.国家电网宁夏电力公司 电力科学研究院，宁夏 银川 750002）

随着控制理论、电力电子技术和稀土永磁材料的快速发展，永磁同步电机正在取代步进和直流电机成为伺服驱动领域新的发展方向［1］。调速永磁同步电动机因其动态性能好，功率密度大、控制器简单等优点在高性能伺服领域中被广泛应用。为降低铁耗、减小转矩脉动和噪声，永磁同步电动机要求永磁体产生的空载气隙磁场（磁通密度，简称“磁密”）成正弦分布［2］。为了优化内置式V型磁体电机的空载气隙磁密波形，文献［3－4］采用不均匀气隙的方法获得了气隙磁密总谐波畸变率与偏心距的关系。但采用不均匀气隙后，转子冲片外围不再是一个标准圆，加大了转子冲片的制造难度和成本。文献［5］研究表明，不等厚度瓦片形永磁体（弧形永磁体）产生的气隙磁密波形比等厚度瓦片形永磁体更接近正弦形，由它感生的空载反电动势主要含基波和3次谐波。为了优化永磁同步电动机的空载气隙磁密波形，文献［6］提出了表贴－内嵌混合式磁极结构，与单一的表贴式、内置式磁体结构相比，这种新型磁极结构气隙磁密波形正弦性好、漏磁少。与常规永磁体结构相比，Halbach永磁体结构电机的气隙磁密波形正弦性好［7］，对电机的高效率、高速运行有益，特别适用于永磁无刷直流电动机［8］。

文献［5－7］改善气隙磁密波形的方法，同时也存在着磁钢加工制造困难、充磁复杂和不易安装等问题。针对这些难题，本文设计出一种结构简单、易充磁、易安装的表贴式永磁体新结构。与瓦片形永磁体结构相比，这种新型永磁体结构产生的气隙磁密谐波幅值小、波形正弦性好，更适用于表贴式调速永磁同步电机。

1 阶梯形永磁体设计构思及数学分析

理论分析和仿真结果表明：对于径向充磁的表贴式调速永磁同步电机，若忽略定子齿槽对磁场分布的影响，永磁体产生的气隙磁密波形具有严格的矩形特征。对于径向充磁的表贴式永磁同步电机（一般采用等厚度瓦片形永磁体结构），其一对永磁体产生的气隙磁密波形可理想化为函数图形，如图1a所示，对应的函数如下：

图1 函数图形

通过傅里叶级数展开，对（1）式做谐波分析。傅里叶级数展开的一般形式为：

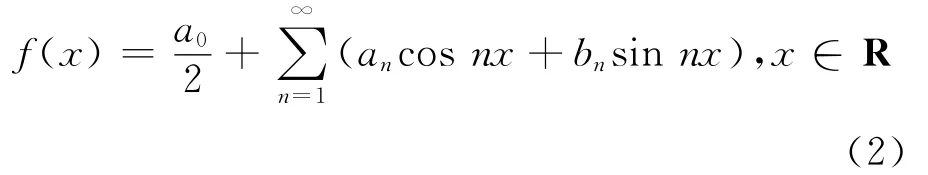
其中，an、bn为傅里叶系数。由于（1）式为奇函数，因此对应的傅里叶级数展开式中只含正弦项，故an＝0。对（1）式周期延拓，然后做傅里叶级数展开，可得：

对 （3）式做进一步分析，假设b＝π－L＝5π／6，a＝L＝π／6，则有：

其中，k＝1，2，3，… 。进而可得（1）式的傅里叶级数如下：

上述分析表明：气隙磁密不含偶次谐波分量，条件是永磁体沿转子圆周必须均匀分布。因此，在安装永磁体时，必须保证相邻永磁体等间距，以削弱气隙磁密的偶次谐波分量。当L＝π／3时，即瓦片形永磁体对转子圆心的张角b－a＝2π／3电角度时，气隙磁密不含3的奇数倍次谐波。

调速永磁同步电动机需要正弦分布的空载反电动势和正弦分布的相电流相互作用产生没有波动的平稳电磁转矩［9］。为了获得正弦分布的空载反电动势，除了采用短距分布绕组外，还可通过优化转子磁极使气隙磁密波形近似呈正弦分布。对于瓦片形永磁体，优化气隙磁密的常用方法是调整极弧系数。其极弧系数αp的计算公式为：

其中，bm为瓦片形永磁体弧长；τ为极距。

文献［10］分析了极弧系数对表贴式调速永磁同步电机感应电动势和漏磁系数的影响，得出表贴式永磁同步电机极弧系数在0.77附近时感应电动势总谐波含量最小，感应电动势取得最优正弦波形，而且漏磁系数随极弧系数的增大而增大。

数学分析表明，当函数形状越逼近正弦形时，它的谐波含量越少。研究发现阶梯形函数比矩形函数能更好地逼近正弦函数，阶梯形函数图形如图1b所示，相应的函数表达式为：

对（7）式进行傅里叶级数展开得：

对（8）式作进一步分析，假设a1＝L1，a2＝L2，b1＝π－L2，b2＝π－L1，且L1＝π／3－L2，A＝2B，则有：

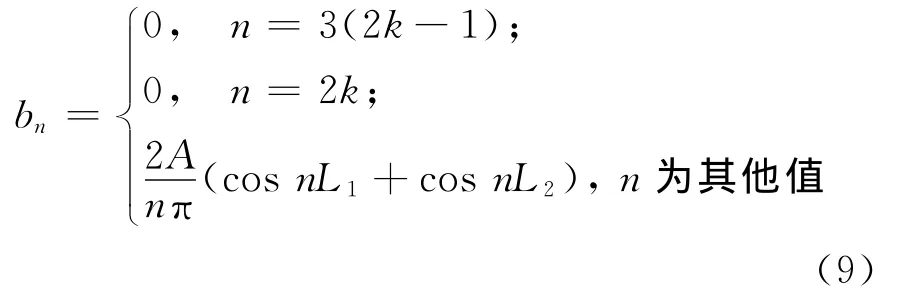
其中，k＝1，2，3，…。

进而可得（7）式的傅里叶级数如下：

上述分析表明，在所述条件下，阶梯形函数（7）式具有（1）式所有特点，不含偶次谐波分量和3的奇数倍次谐波。为保证（7）式的基波分量幅值足够大，L1及L2取值应尽可能小。若使L1＝π／12，L2＝π／4，L＝π／6，则有：

当且仅当n为12的倍数时，不等式两边取等号。由于（1）式与（7）式均不含偶次谐波，故不等式左边恒小于右边。对比 （4）式和 （9）式，可得（7）式的非零谐波幅值恒小于（1）式。在假设条件下（7）式的基波幅值降为（1）式的0.97倍，但带来的好处是其非零谐波分量幅值均降低。

鉴于阶梯形函数谐波分量幅值小的优点，本文设计出了一阶梯形永磁体转子结构，这种阶梯形永磁体转子结构及常规的瓦片形永磁体转子结构示意图如图2所示。其中，1表示转轴；2表示转子铁芯；3表示磁钢1；4表示磁钢2；α表示磁钢1对转子圆心的张角；β表示磁钢2对转子圆心的张角。

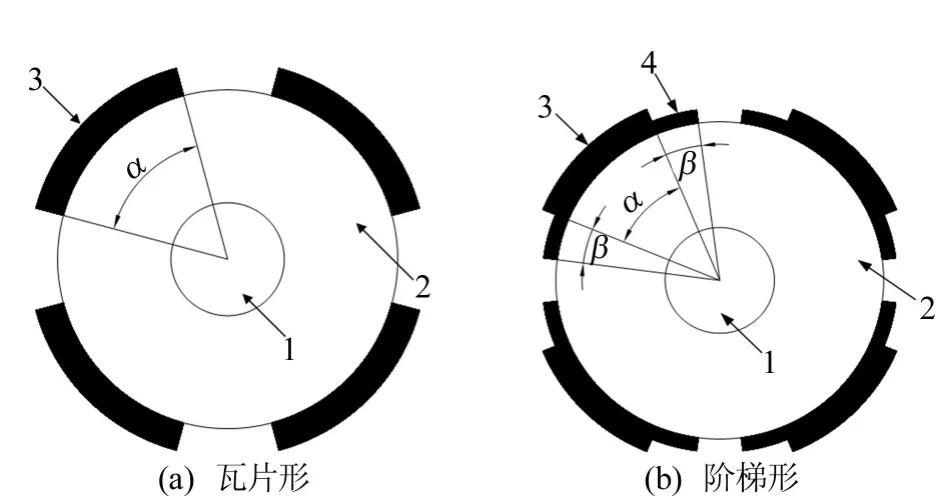
图2 调速永磁同步电机转子结构

在分析阶梯形永磁体设计前，做以下假设：① 忽略定子齿槽的影响，将所研究的电机理想化为一无槽电机；② 不计铁芯磁阻和永磁体内磁阻；③ 认为永磁体为各向同性媒质，并均匀磁化；④ 不计永磁体的漏磁。

当所有磁钢均采用同一种永磁材料，并且采用径向充磁时，则有：

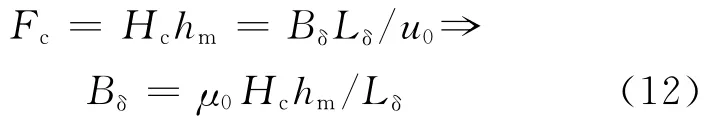
其中，Fc为永磁体虚拟内稟磁动势；Hc为永磁体的矫顽力；hm为永磁体厚度；Bδ为气隙磁密；Lδ为单边气隙长；μ0为真空磁导率。当Hc、μ0及Lδ保持不变时，Bδ正比于hm。因此，在气隙长度和永磁体材料确定的条件下，保证磁钢1厚度为磁钢2的2倍，那么磁钢1产生的气隙磁密便是磁钢2的2倍。

将永磁体沿转子圆周展开，并建立直角坐标系，如图3所示。坐标系原点为相邻两磁极中心线与转子铁芯外圆周的交点；y轴为沿转子铁芯径向方向，其值表征永磁体的厚度；x轴为沿转子铁芯圆周方向，其值表征转子外圆周对转子圆心的张角，单位为电角度。

从图3中可知，将区域1、2两部分的永磁体分别搬移到区域3、4，瓦片形永磁体便转变为阶梯形永磁体。从中可得到移动的永磁体体积V＝wplph／2，其中，wp为移动的永磁体宽；lp为移动的永磁体轴向长；h／2为移动的永磁体高度。保持lp、h不变，移动的永磁体体积仅决定于wp。从图3可得，wp最小取值为0，最大取值π／6。wp取不同的值，可得到不同尺寸的阶梯形永磁体，不同尺寸的阶梯形永磁体的气隙磁密谐波情况也不同。基于前述的数学分析，对瓦片形永磁体结构，选定α＝π／3；对阶梯形永磁体结构，选定α＝π／4，β＝π／12，并且磁钢1和2采用同一种永磁材料。

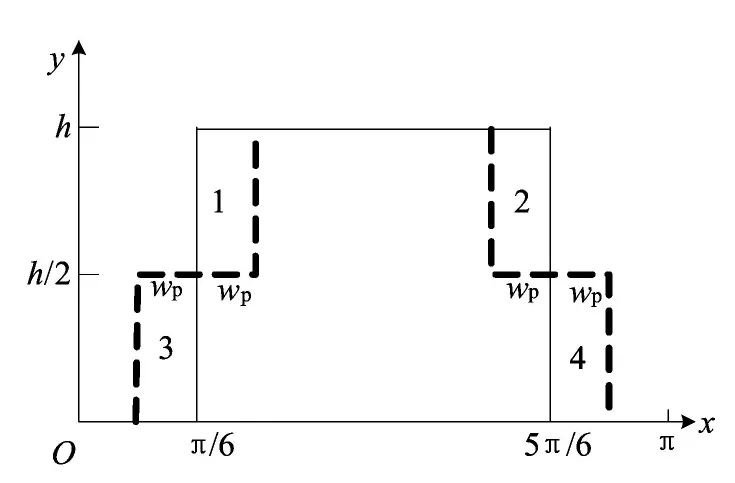
图3 永磁体沿转子圆周展开图

2 有限元仿真实验及结果分析

为了论证上述理论的正确性，本文研究3kW、4极表贴式调速永磁同步电机模型，电机的具体结构参数如下：定子槽数为24；定子外径为155mm；定子内径为94mm；气隙长度为0.4mm；磁化方向长度为2mm；转子外径为89.2mm；转子内径为38mm；轴向长为96mm。磁钢采用优质磁性材料铷铁硼，牌号为N38SH；定、转子采用优质冷轧硅钢片50DW600。

在电磁场分析软件Magnet中分别搭建了瓦片形调速永磁同步电机和阶梯形调速永磁同步电机二维有限元仿真模型并做仿真，并对这2种永磁电机的气隙磁密波形和反电动势波形进行研究分析。

2.1 气隙磁密仿真结果对比分析

仿真所得的气隙磁密波形如图4所示，图4只给出一对极范围内的气隙磁密，以便对比分析。从波形轮廓上看，图4b比图4a更接近正弦波。波形图中的凹凸是由于定子开槽引起的。

对仿真得到的磁密数据做谐波分析，结果如图5所示。对比瓦片形永磁体结构和阶梯形永磁体结构的气隙磁密谐波，发现两者均不含偶次谐波，而且3的奇数倍次谐波基本为0；1阶齿谐波（11、13次谐波）受周期性齿磁导的“放大”作用，后者比前者大；后者基波幅值略小于前者基波幅值，但后者谐波幅值得到很大抑制，其中5、7、11次谐波幅值比前者明显减小。为了对比这2种气隙磁密波形谐波含量的大小，本文引入总谐波失真率THD，其计算公式为：

其中，下标表示谐波次数，最大谐波次数为512；B1为气隙磁密的基波幅值。计算出的气隙磁密波形THD见表1所列，从表1可知，阶梯形永磁体的气隙磁密谐波含量相对较小。

图4 气隙磁密波形

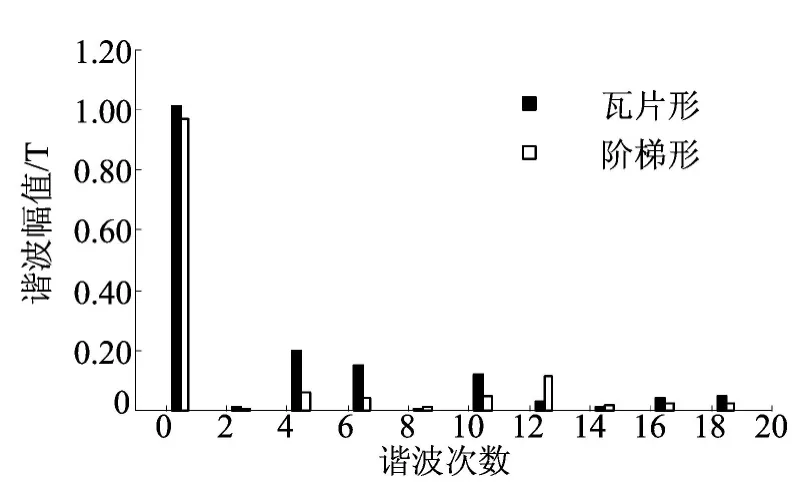
图5 气隙磁密谐波

表1 总谐波失真率

电机理论表明，对于正规的60°相带绕组，三相合成磁动势中存在6k±1次谐波（其中包含5、7、11次），并且随谐波次数的增加谐波幅值逐次减小。就永磁同步电机而言，三相合成磁动势所产生的气隙磁场与永磁体产生的气隙磁场相互作用产生转矩。两者基波磁场相互作用产生主要电磁转矩，它决定着电机负载能力的大小。其他次谐波磁场相互作用产生附加电磁转矩，附加电磁转矩对基波电磁转矩来说是一种干扰，对电机的稳定运行和控制均不利。另外，削弱谐波（尤其是5、7、11次）幅值，可减小电机的振动噪声、减小电机损耗、提高效率。传统抑制谐波的方法是采用短距绕组，该方法仅适用于双层绕组。至于永磁同步电动机可采用特殊永磁体结构（如阶梯形永磁体结构）来抑制谐波。这样定子绕组就不必局限于短距绕组（如采用单层绕组、整数槽绕组），从而增加了定子绕组设计的灵活性。气隙磁密谐波幅值的降低对改善反电动势波形、削弱齿槽转矩是有益的。这些决定了采用阶梯形永磁体结构比采用瓦片形永磁体结构具有一定优越性。

2.2 反电动势仿真结果对比分析

仿真得到的三相反电动势波形如图6所示。从图6可以看出，瓦片形三相反电动势波的顶部近似为平顶，而阶梯形三相反电动势波的顶部近似为圆弧形，因此阶梯形的三相反电动势波形更逼近正弦波。

图6 三相对称绕组的反电动势波形

对其中一相绕组的反电动势进行谐波分析，结果如图7所示。由图7可知，两者3次谐波电动势基本为0；5次、7次谐波反电动势幅值阶梯形明显低于瓦片形。2种反电动势波形的THD计算值见表1所列，从表1可以看出，阶梯形永磁体的反电动势谐波含量相对较小。电机反电动势谐波含量的减小，不仅对减小电机本身的杂散损耗、提高电机效率有益，而且有助于减弱电机运行时对电网造成的谐波污染。

图7 一相绕组反电动势谐波

3 结束语

理论分析和仿真后的数值分析均表明，在一定的条件下，阶梯形永磁体产生的气隙磁密谐波幅值比传统瓦片形永磁体小，尤其是5、7、11次。这种阶梯形永磁体结构，不仅具有瓦片形永磁体结构充磁简单、磁极安装方便的优点，还可达到优化气隙磁密的目的。

［1］ 唐任远.现代永磁电机理论与设计［M］.北京：机械工业出版社，1997：161－215.

［2］ 王成元.现代电机控制技术［M］.北京：机械工业出版社，2006：104.

［3］ 徐英雷，李群湛，王 涛.永磁同步电动机空载气隙磁密优化［J］.西南交通大学学报，2009，44（4）：514－516.

［4］ 徐衍亮，许家群，唐任远.永磁同步电动机空载气隙永磁磁密波形优化［J］.微特电机，2002（6）：5－6.

［5］ 常九健，马文礼，黄金龙.永磁同步电机永磁体形状分析和优化［J］.大电机技术，2012，（2）：16－17.

［6］ Si Jikai，Si Meng，Teng Haichao.Research on the field of new type rotor structure permanent magnet synchronous motors［J］.Applied Mechanics and Materials，2012，143：154－158.

［7］ 徐衍亮，姚福安，房建成.Halbach磁体结构电动机及其与常规磁体结构电动机的比较研究：Ⅰ［J］.电工技术学报，2004，19（2）：80－81.

［8］ Zhu Ziqiang.Recent advances on permanent magnet machines［J］.Transactions of China Electrotechnical Society，2012，27（3）：3－4.

［9］ 王秀和.永磁电机［M］.北京：中国电力出版社，2011：278.

［10］ 翟秀国.表面贴装和内嵌式永磁同步电机轮毂电机的研究［D］.北京：北京交通大学，2012.