基于稀疏表达的人脸遮挡物去除

吴从中， 刘渠芬， 詹 曙

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

0 引 言

人脸识别技术因其广泛的应用前景成为近年来模式识别和计算机视觉领域的研究热点，并取得了巨大的发展。随着光电技术、微计算机技术、图像处理技术、模式识别技术以及生物特征识别技术的不断发展，人脸识别技术逐步成为国内外热门的新兴学科。

在过去的几十年中，研究人员提出了很多方法来解决人脸识别问题［1］，而由于环境因素的非约束性，姿态、光照、遮挡是目前基于图像的人脸识别系统中几个重要但难以解决的问题。

传统的遮挡下人脸识别方法多将重点放在通过图像的预处理来去除眼镜等遮挡物的影响。一类方法是通过对图像分块来提取图像未被遮挡的稳定特征，如文献［2］对人脸图像分块后，再采用最近邻分类来选择特征，后来又有概率模型和计算区域遮挡权重等方法，但这类方法都取决于区域检测的效果，且不能充分利用人脸特征。另一类方法是通过图像重建来恢复无遮挡的人脸图像，文献［3－4］提出了基于PCA建模的不同方法，这些方法根据有遮挡图像在无眼镜图像空间中的投影系数重建出对应图像，这类方法对于镜片反光和模糊的人脸图像，重建效果很差。对于眼镜遮挡的去除问题，文献［5］提出了基于区域检测的通过关键点的迭代得出眼镜的形状、再通过区域补偿的方法来去除眼镜遮挡的方法，该方法比较复杂，对于墨镜、镜片反光等极端情况效果很差。

本文研究的重点是正面人脸图像中遮挡物的去除问题，提出了基于稀疏表达分类的方法来去除遮挡。首先在训练集上，求出有遮挡的人脸图像对应的稀疏系数，然后根据系数恢复重建出无遮挡的正面人脸图像。采用这种方法可以获得高质量的、无遮挡的人脸图像。

1 基于PCA重建的遮挡去除方法

为解决眼镜遮挡的人脸识别问题，文献［4］提出了基于PCA的重建方法，该方法的主要思想是通过对多幅不戴眼镜样本的训练，重建出测试样本（戴眼镜图像）的不戴眼镜的图像，具体实现方案有2种。

（1）假设训练集有N＋1幅图像yi，其中N幅是不戴眼镜的图像，1幅是戴眼镜的图像，利用PCA提取训练样本集的特征空间，可以得到特征空间的基向量αi（i＝1，…，M），对于任意一幅戴眼镜的图像x在特征空间的投影都对应一组系数，把表示眼镜特征的特征脸的系数赋为0，其他系数保持不变，则该组系数与特征向量的内积所形成的图像就是原输入图像移除眼镜后的图像x＊，即

（2）假设图像集中N幅图像均是不戴眼镜的人脸图像zi，首先利用PCA降维训练得到训练集的特征空间，并得到该特征空间的基向量vi。对于任意输入的戴眼镜的测试图像x，在该特征空间上投影都可以得到一组系数，使用这组系数和基向量的内积就可以得到测试图像移除眼镜后的图像x＊，即

该方法对于眼镜遮挡虽然同时考虑镜片和镜框的影响，但是重建的无眼镜遮挡的图像仍有镜框的痕迹，并且对于墨镜、镜框与眉毛重叠等极端情况重建的效果较差。基于PCA重建的去除眼镜的实验结果如图1所示。

图1 基于PCA重建的去除眼镜的实验结果

2 基于稀疏表达的人脸遮挡去除

2.1 稀疏表达分类

对于样本集的任一类测试样本y，首先计算其稀疏系数x。理想情况下，在x里的非0分量的位置代表了样本集里相关的类，可以容易地判断出测试样本y所属的类。在实验中往往会有噪声的干扰和模型的误差导致分类的错误。在分类时，可以采取设计好的分类器来解决，例如直接把测试样本y划到向量x的最大分量所对应的类，但是这样不利于人脸识别的子空间的关联性。为了较好地保持子空间的线性结构，本文采用最近邻法来进行分类，速度较快。

稀疏表达分类（sparse representation classification，SRC）［6－7］具体步骤如下：

（1）输入。包含k类的训练样本集A＝［A1，A2，…，Ak］∈Rm×n、测试样本y以及可调的容错项ε。

（2）对训练样本集A进行归一化，方便后续的计算。

（3）求解l1范数，即

或者求解

（4）计算残差，即

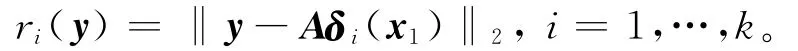
（5）输出。y＝arg minri（y）。

在开始对测试样本进行分类前，需要核查该样本是不是训练集中的样本。实际环境中人脸识别系统不仅要求有较高的识别效率，还要能区分是不是样本集中的数据。

传统的分类器常用的方法有最近邻或最小距离，然后使用残差来判断。然而，对于任一类残差都没有任何先验知识，只能通过计算每个样本和每一类之间的相似度来得到。

在范例中，对于所有类来说，向量x1是通过全局计算得到的，从某种意义上说，它可以利用所有验证类的联合分布。本文认为在统计验证方面，系数x是比残差更好的数据。

为了更好地对样本进行分类，定义SCI（sparsity concentration index）为：

对于求得的稀疏系数x，如果SCI（x）＝1，即表示仅用了某一类的一个图片来表示测试图像，这样可以准确无误地进行分类；如果SCI（x）＝0，则表示稀疏系数横跨所有的类，这时对测试图像进行分类，准确率很低。在实验过程中，设置一个阈值τ（0，1），如果SCI（x）≥τ（0，1），则接受这幅测试图像。

2.2 基于稀疏表示的人脸重建

在生活环境中，常常会有遮挡或是损坏的人脸图像，干扰识别的效果。在没有遮挡的人脸图像训练集中，测试样本y表示为：

其中，A为训练样本集；x的解是最稀疏的。

如果测试样本中有遮挡的人脸图像，则（4）式修正为：

其中，e0∈Rm为冗余向量，对应着人脸图像中损坏或遮挡的部分。由于遮挡的位置和大小是随机的，针对不同类型的遮挡，比如围巾或者眼睛，冗余项e0是可变的。每种不同的遮挡，构造出不同的e0，保证图像后期恢复重建的质量［8－9］。假设遮挡部分的区域比较小，冗余项e0和x0一样都是稀疏系数，（5）式可重写为：

其中，B＝［A，I］∈Rm×（n＋m）。（6）式是个签订方程，存在多解。本文的目标是在其中寻找最稀疏的解，实验表明，遮挡面积在小于50%的情况下，最稀疏的系数解ω0就是真实解。

一般来说，冗余向量e0对于一些正交基Ae∈Rm×ne有稀疏性，即e0＝Aeu0。其中的正交基Ae可以是傅里叶变换或者小波变换等。简化矩阵B的表达，即

这样转变以后可以处理多种遮挡或者不同程度的损坏等情况，比用单位阵来表示更有针对性，效果也更好。通过求解ω0的l1范数来寻找最稀疏系数解，因为在多数情况下，l1范数和l0范数是同解的。l1范数的表达式如下：

其中，B＝［A，I］；ω＝［x，e］。

从上述可知，l1范数的最小化取决于多面体P＝B（P1）＝［A，I］（P1）。在样本集A和矩阵I里找到的多面体的顶点就是要求的稀疏解。对于一个给定的样本集，能够处理多大的遮挡区域，需要通过相关算法验证。

稀疏解ε＝［x1，e1］得到之后，令yr＝y－e1，则残差修正为：

3 实验结果

（1）实验1。在AR人脸库上进行去遮挡实验，选择10个人的正面图像，每个人选择5副无遮挡图像作为训练，去除遮挡后的正面人脸图像如图2所示。

图2 基于稀疏表达的去除墨镜、围巾遮挡的实验结果

图3 基于稀疏表达的去除视频中眼镜图像的实验结果

（2）实验2。在视频中截取了一系列的图像作为实验对象，选择10个人的正面图像，每个人选择8幅作为训练图像，得到的去除眼镜的对比图像如图3所示。实验证明，该方法不仅能够有效地去除普通眼镜遮挡，并具有一定的鲁棒性，对存在墨镜、围巾遮挡这样的极端情况也具有很好的重建效果，而且能够克服光照、表情等变化的影响，具有一定的实际应用价值。

4 结束语

对于人脸识别过程中的遮挡问题，本文根据稀疏表达的相关知识提出了一种新的去遮挡方法，根据欠采样的原理，在有限少量的信息情况下依旧可以恢复出原始信号的思想，并通过实验，采样有遮挡的图像，对得到的信息进行恢复重建，获得没有遮挡的人脸图像。与传统的去遮挡方法相比，本文方法更简洁、有效。算法中不同类型遮挡的字典构造是以后进一步的工作方向。

［1］ 王 伟，张佑生，方 芳.人脸检测与识别技术综述［J］.合肥工业大学学报：自然科学版，2006，29（2）：158－163.

［2］ Oh H J，Lee K M，Lee S U，et al.Occlusion invariant face recognition using selective LNMF basis images［M］／／Computer Vision－ACCV 2006.Berlin：Springer－Verlag，2006：120－129.

［3］ Saito Y，Kenmochi Y，Kotani K.Estimation of eyeglassless facial images using principal component analysis［C］／／International Conference on Image Processing.IEEE，1999：197－201.

［4］ Park J S，Oh Y H，Ahn S C，et al.Glasses removal from facial image using recursive error compensation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（5）：805－811.

［5］ Wu C，Liu C，Shum H Y，et al.Automatic eyeglasses removal from face images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26 （3）：322－336.

［6］ Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31（2）：210－227.

［7］ 李 映，张艳宁，许 星.基于信号稀疏表示的形态成分分析：进展和展望［J］.电子学报，2009，37（1）：146－152.

［8］ Yang M，Zhang D，Yang J.Robust sparse coding for face recognition［C］／／IEEE Conference on Computer Vision and Pattern Recognition.IEEE，2011：625－632.

［9］ Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53（12）：4655－4666.