海流传感器的结构设计及优化

王云燕， 王 勇， 王晓锋， 鲍艳艳， 龙 灿

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

流速是流体的一个重要基本参数，流速测量一直备受关注，如海洋流场的实时监测和测量是海洋科学考察的重要内容，实时监测海流变化可以对气候进行及时预测，提出防范规则［1－2］。

虽然流速测量仪器种类繁多、各具特色，但是目前的毕托管式差压流速传感器、机械式转子流速传感器、电磁式流速传感器、热式流速传感器、多普勒声学流速传感器以及PIV粒子成像测速仪等，或测量精度难以提高，或存在转动部件，或成本较高价格昂贵，或对工作环境有特殊要求［3］。而应变式传感器不仅结构简单、操作方便、测量精度高、价格低廉，而且对工作环境几乎没有要求［4］。应变式传感器的优劣取决于弹性体设计的好坏，弹性体的设计和优化是其核心技术［5－6］。

本文介绍了一种应变式十字梁海流传感器的结构和原理，建立了传感器的模型，分析了弹性体的应变分布［7］，得到了传感器的贴片位置。为了实现对较低海流的精确测量，需要对弹性体尺寸进行优化，但对传感器弹性体关键参数的不同尺寸任意组合进行数值计算，计算量太大，且结果仍然不能提供充分的信息。故在对十字梁海流传感器弹性体关键参数单因素优化的基础上，结合正交试验方法综合优化［8］，以期最大限度地减少计算量，能较全面地分析十字梁海流传感器弹性体关键参数对其应变和固有频率的影响。

1 十字梁海流传感器的原理

1.1 十字梁海流传感器的结构

十字梁海流传感器的测量装置由圆球、圆柱固定杆、中心盘、十字弹性梁（弹性体）、弹性梁支架组成，其总体结构如图1所示。

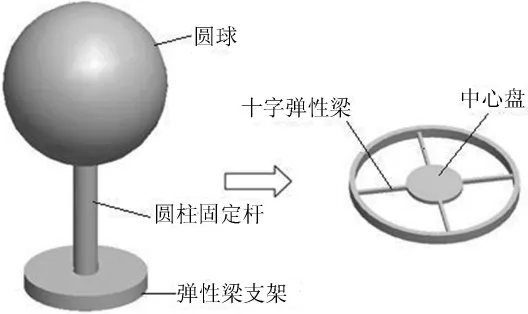
图1 十字弹性梁结构简图

圆柱固定杆上端固定圆球，下端通过一法兰盘与弹性梁中心盘连接；圆球通过一圆柱固定杆与中心盘刚性连接，故可将中心盘视为刚体；下端由中心盘和4根正交弹性梁组成，且为一整体，采用平面坐标内对称方式布置。弹性梁对称性设计能有效减小维间耦合、降低温度等因素的影响，且结构简单；中心盘截面尺寸较大，抗弯截面系数大。通常，传感器受到的应力在弹性梁的线弹性范围内，且变形较小，因此载荷与应变、位移成线性比例关系。

1.2 十字梁海流传感器的原理

在实际的海流中，球壳会受到水平流产生的二维水平作用力，该作用力通过圆柱固定杆和中心盘对十字弹性梁产生二维力矩，布置在2个方向上的十字弹性梁上、下的敏感元件分别受到拉应力或压应力。由1个方向上的敏感元件构成的电桥可以获得该方向上的力矩，由2个方向的力矩可以合成二维力矩的大小和方向，根据该力矩可求出水平作用力的大小和方向，再根据标定的水平作用力和流速间关系可以获得水平流速的大小和方向。

选用应变片作为敏感元件，通过惠斯通电桥把流速信息转化为电信号，此技术成熟且精度高，可有效地降低传感器的制作成本。

2 传感器弹性体应变的仿真计算

2.1 传感器弹性体材料选择

传感器弹性体材料选用铝合金LY12，其弹性模量E＝72 000MPa，密度ρ＝2 778.7kg／m3，泊松比μ＝0.3，抗拉强度σb＝5×108N／m2；条件屈服强度σs＝3.8×108N／m2。

2.2 弹性体的建模分析

将海流传感器模型放置在海流中进行流体模拟计算的情况，如图2所示，此处详细内容可参见文献［9］。

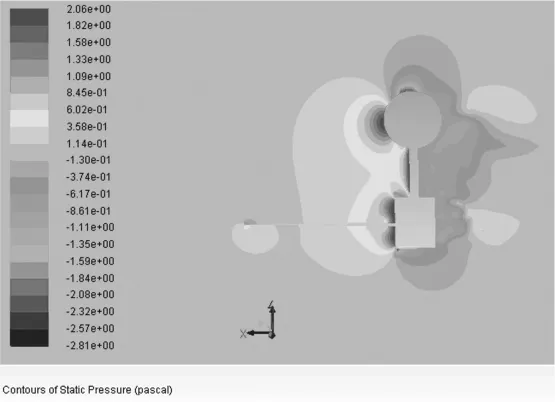
图2 模型流体分析云图

在流体计算的基础上，得到流速在16～100mm／s之间时作用在圆球上的阻力。弹性梁的长、宽、高分别为l＝45mm、a＝3mm、h＝3mm，中心盘直径为r＝30mm。

在弹性梁的端末用固定约束，在中心盘的中心施加绕Y轴的力矩Me＝13.9N·mm和沿X正方向的力Fx＝6.95×10－2N，分析弹性梁在不同载荷时的应变变化情况，结果见表1所列。其中，U0为来流速度；Fd为圆球阻力；εmax为弹性梁最大应变。

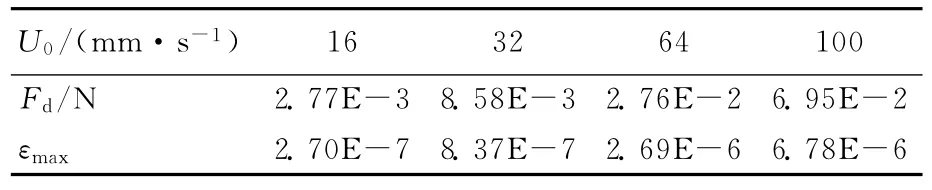
表1 流速对应的圆球阻力及梁的最大应变

由表1可知，当流速为32mm／s时，弹性梁产生的最大应变仅为8.37×10－7，而普通应变片的测量精度为微米级，无法测量出10－7数量级的应变，所以弹性梁也就无法测量到32mm／s及更小的流速。为了使设计的传感器能测量32mm／s及更小的流速，就需要对弹性梁进行优化设计。

2.3 弹性梁的贴片位置

流速为100mm／s的弹性梁上产生的应变分布情况如图3所示。由图3可知，弹性梁的最大应变主要产生在它固定端和中心盘根部附近，梁中间附近应变最小，即应变沿梁长度方向的分布是先逐渐减小至0后逐渐增大，中间附近为0。所以，应变片应该贴在每根弹性梁两端的上、下面上。每根弹性梁上、下面各贴有2片，共采用16片应变片，如图4所示，数字所在位置代表应变片在弹性梁此处的上、下表面上的贴片位置。

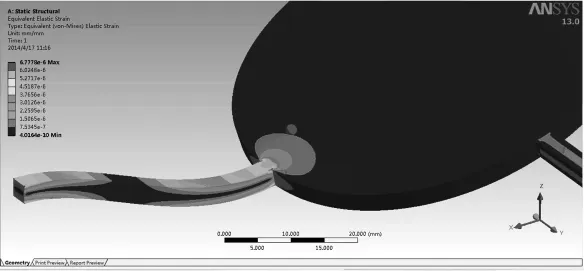
图3 弹性梁的应变分布云图

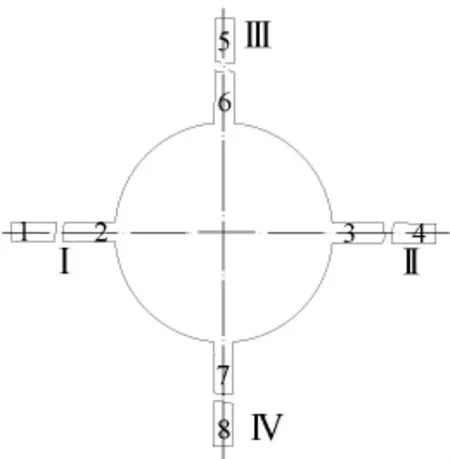
图4 弹性梁上应变片分布图

当有沿X方向的分力Fx作用时，弹性梁Ⅰ、Ⅱ产生弯曲变形，弹性梁Ⅲ、Ⅳ产生扭转变形，应变主要由弹性梁Ⅰ、Ⅱ根部上下表面的应变片1、2、3、4提供。当有沿Y方向的分力Fy作用，分析过程同X方向，应变主要由弹性梁Ⅲ、Ⅳ根部上、下表面的应变片5、6、7、8提供。

3 正交试验优化设计

由于梁的长度、宽度、高度的变化范围很大，直接进行正交试验不能找到对应的正交表，且计算量非常大。为了能在较大范围内确定梁关键参数的最优尺寸，且兼顾计算量较小，可先对梁的关键参数进行单因素优化，即分别讨论梁的长度、宽度、高度的变化对应的应变情况，根据结果曲线选取每个参数相对较优的1组数据，由这3组数据进行正交试验，以期得到模型的最优尺寸。

3.1 梁长、梁宽、梁高的单因素优化

材料不变、载荷输入不变的情况下，梁的长度、宽度和高度分别在一定范围内变化时，分析梁应变的变化曲线，如图5所示。

图5 应变随梁长、梁宽、高变化图

由图5a可知，当梁的长度为33、35、37mm时对应的应变最大，故梁长度选取为33、35、37mm；由图5b中的高度曲线变化可知，梁的最大应变随梁高度的增大而减小，而高度在0～2mm内变化时，应变的变化非常大，此后随着高度的降低，应变的变化比较平缓，故选取梁的高度为1.5、2.0、2.5mm；分析图5b中的宽度曲线，发现梁的最大应变也随梁宽度的增大而减小，但为了使梁有足够的抗弯能力，并兼顾应变最大，选取梁的宽度为2.5、3.0、3.5mm。

3.2 正交试验设计

传感器的结构复杂且设计参数多，如对不同结构参数任意组合进行数值优化分析，计算量太大，且计算结果仍不能充分反映各结构参数对传感器性能的影响程度。因此，本文采用正交试验设计，以期最大限度地减少计算量，较全面地分析弹性梁关键参数对传感器静、动特性的影响［9］。

按照正交试验的方法来设计试验方案，选取弹性梁长度A、宽度B、高度C3个因素，根据3.1节的分析结果，每个因素选择3个水平进行试验方案的确定，见表2所列。为了兼顾弹性梁的动态特性，保证梁有良好的动态性能，选取梁的最大应变和固有频率为试验指标。因此这是3因素3水平的多指标问题，选择L9（33）正交试验表，表3给出了9组水平组合对应的最大应变和梁的固有频率的分析结果，以及采用2指标试验的极差分析法对试验数据的分析。

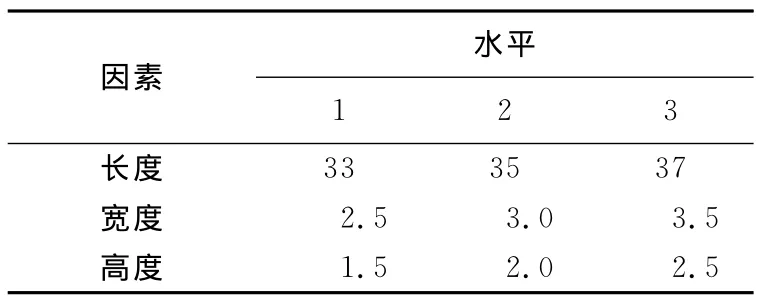
表2 因素水平表 mm

由表3可知，高度的变化对模型试验指标的影响最大、宽度次之、长度最小。兼顾梁的应变和固有频率不低于10Hz，可确定一组相对较好的方案A1B2C1，即梁长33mm、宽3.0mm、高1.5mm。此时，梁的固有频率为10.491Hz，满足了动态设计要求。

建立新模型，再对新模型施加载荷，分析其在不同流速时的最大应变，结果见表4所列。

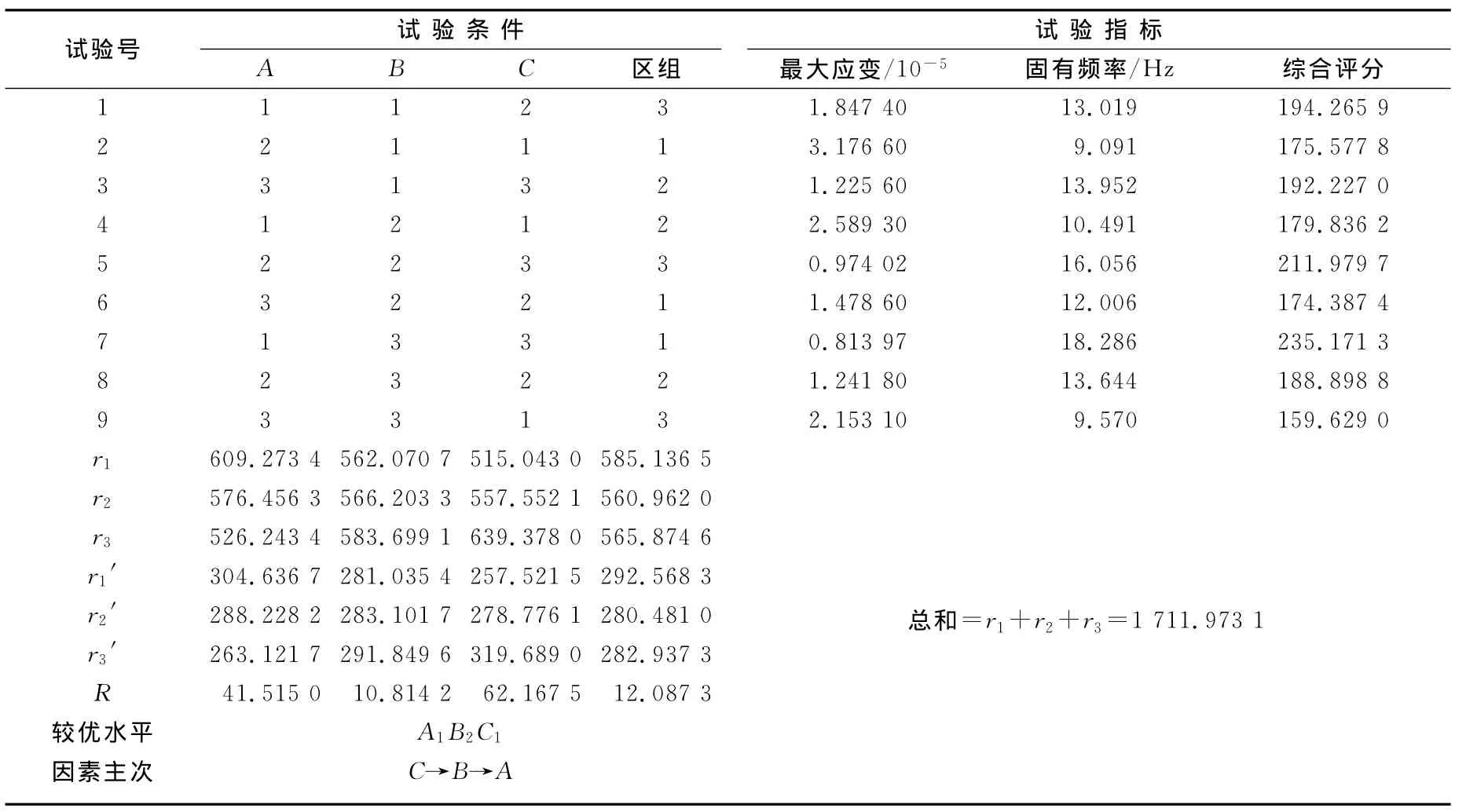
表3 正交试验表和极差分析结果

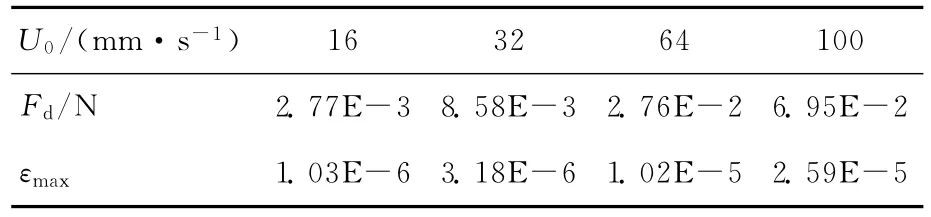
表4 流速对应的圆球阻力及优化梁的最大应变

由表4可知，优化后弹性梁在流速为16mm／s时，产生的应变为1.03×10－6，达到了应变片的测量要求，因此设计的传感器最小可测量到16mm／s的流速。又弹性梁在线弹性范围内，其产生的最大应变εmax≈5.27×10－3，根据流体计算得到的流速和应变之间的规律，可知此时对应的来流速度U0≈1 420mm／s。因此可以推断，优化后的海流传感器可测量的水平流速的范围约为16～1 420mm／s。

综上所述，优化的结果不仅使传感器的测量范围更大、测量精度更高，也保证了弹性体的固有频率不低于10Hz。结果不仅达到了优化海流传感器的目的，也提高了弹性体的动态特性。

4 结束语

本文设计了一种应变式十字梁海流传感器，由仿真分析结果给出了弹性梁应变片的贴片位置。采用关键参数单因素优化和正交试验综合优化相结合的方法对传感器弹性体结构进行优化，结果不仅使传感器实现了测量16～1 420mm／s海洋流速的目的，也保证了其固有频率不低于10Hz，扩大了传感器的测量范围，提高了弹性体的动态特性，减少了实验次数与计算量，达到了传感器结构优化设计的目的。设计的应变式海流传感器结构简单、操作方便、量程大、价格低廉、对工作环境几乎没有要求，可广泛应用于各种需要海流测量的场合，有良好的发展前景。

［1］ 韦祥杨.时差法三维流速测量技术研究［D］.哈尔滨：哈尔滨工程大学，2009.

［2］ 孙敬慧.三维流速传感器力标定系统的研究［D］.合肥：合肥工业大学，2011.

［3］ 王 勇.一种三维力流速传感器：中国，201010111455.2［P］.2010－07－14.

［4］ 干方建，刘正士，任传胜，等.一种应变式多维力传感器的优化设计［J］.传感器与微系统，2007，26（1）：56－59.

［5］ 宋 伟，张 新，王 磊.基于正交试验的应变式六维力传感器弹性体结构的优化设计［J］.工矿自动化，2009，35（10）：60－62.

［6］ 程晓晓，王秋晓.平行梁式传感器弹性体的设计与有限元分析［J］.重庆理工大学学报：自然科学版，2011，25（4）：55－60.

［7］ 许 斌，秦 岚，薛 联，等.基于ANSYS的压电四维力传感器一种优化设计方法［J］.传感器技术学报，2011，24（1）：36－40.

［8］ 吴宝元，申 飞，吴仲城.应变式多维力传感器结构优化设计方法研究［J］.传感技术学报，2010，23（10）：1412－1416.

［9］ 郑 双，高荣慧，王 勇.重力场下垂直微力发生装置的研究［J］.合肥工业大学学报：自然科学版，2014，37（2）：134－136，163.