基于绿色再制造的废旧汽车发动机最优回收价格决策

范 俊， 晋盛武

（1合肥工业大学 经济学院，安徽 合肥 230601；2.合肥工业大学 工业信息与经济研究中心，安徽 合肥 230601）

在环境污染和自然资源日益枯竭的双重压力下，人们越来越重视废旧产品的回收绿色再制造问题［1］，作为进行废旧产品回收绿色再制造的主体——再制造工厂应运而生。然而在再制造工厂管理中，如何将废旧产品的回收供给与再制造产品的需求通过价格杠杆进行匹配是非常关键的环节［2－3］，它直接影响后续的绿色再制造活动。因此，国内外学者在废旧产品回收定价问题上的研究成果丰硕。文献［4］指出原始设备制造商（OEM）更倾向将废旧产品回收及再制造外包给其他企业，产生了回收商驱动渠道、再制造商驱动渠道以及回收商与再制造商集中渠道，根据回收定价决定OEM应该选择哪种渠道的结论；文献［5］基于一个具有可控随机输入的库存模型来确定回收中心回收废旧产品的最优定价策略，证明了依赖于初始库存等级的关键值策略为最优定价策略；文献［6］分析在Stackelberg博弈和集中式决策2种情形下的回收商最优回收价格、制造商最优回购价格；文献［7］考虑单一制造商和单一零售商构成的二级供应链、逆向供应链系统的定价和协调机制，双方联合定价将带来最优结果；文献［8］考察了制造商生产的最优策略受到新产品生产和回收品再制造商的启动成本影响。

从上述文献可看出，目前关于废旧产品回收定价研究多集中于以制造商、回收商为主体，且研究的内容都是从消费者手中回收废旧产品的定价问题，以独立的再制造工厂为主体研究从回收商手中回收废旧产品定价问题的文献还较少。文献［9］以美国最大手机翻新厂商ReCellular为研究主体明确提出采取回收定价来控制回收品数量的定量模型；文献［10］研究再制造商作为Stackelberg领导者，预测到分销商的反应并据此选择最优的回收价格和批发价格。本文以我国汽车发动机再制造为例，基于由消费者、汽车4S店售后修理部、汽车发动机再制造工厂和汽车4S店售后配件部组成的废旧汽车发动机回收再制造逆向供应链，建立数量模型确定汽车发动机再制造工厂应采取最优回收价格决策。

1 模型假设与问题描述

本文依据的案例是大众汽车集团和中国一汽集团合资建立的汽车发动机再制造厂对废旧汽车发动机进行回收再制造，案例中涉及的废旧汽车发动机回收再制造供应链如图1所示。

图1 以再制造工厂为中心的废旧汽车发动机再制造供应链

废旧汽车发动机回收再制造供应链流程如下：

（1）废旧汽车发动机质量等级标准由再制造工厂设置，设其为n＝1，2，…，K。

（2）汽车发动机再制造工厂接受来自于汽车4S店售后配件部的订单，订单载明的信息包括：① 汽车4S店售后配件部预测对再制造汽车发动机的需求，用d表示，为常数；② 汽车4S店售后配件部向汽车发动机再制造工厂提供一台再制造汽车发动机的价格为Pn。

（3）汽车4S店售后修理部向再制造工厂提供废旧汽车发动机的供应量Sn为随机变量，预测供应量参数（均值μn和标准差σn），其概率分布函数为F（Sn），概率密度函数为f（Sn）。

（4）供应量的随机性会导致汽车发动机再制造工厂回收的废旧汽车发动机的数量与其需求量不能完全匹配。若汽车发动机再制造工厂回收废旧汽车发动机数量大于其需求量时，每台废旧汽车发动机残值为r0；若其回收量小于需求量，短缺一台废旧汽车发动机的处罚值为P0。

（5）为达到消费者对再制造汽车发动机所需的质量要求，汽车发动机再制造工厂需要从市场上采购一组额外的汽车发动机替换零件，将其与采购回来的废旧汽车发动机进行整合加工，设质量等级为n的废旧汽车发动机所需额外替换零件成本为bn。

（6）汽车发动机再制造工厂根据上述信息，估计从汽车4S店售后修理部回收废旧汽车发动机的最优价格pn以及最优数量qn。

为了便于分析，进一步对模型作如下假设。

（1）汽车发动机再制造工厂在质量等级n的初始废旧汽车发动机库存量为Xn。

（2）汽车发动机再制造工厂提供给售后修理部一台废旧汽车发动机的价格满足pn＝P0－bn，则导致其回收的废旧汽车发动机过多，严重降低其利润水平；而若价格满足pn＝r0，则较低的回收价格抑制了售后修理部向再制造工厂提供废旧汽车发动机。故认为pn范围为r0＜pn＜P0－bn。

（3）设运输成本为单位运输成本、收购数量和运输距离的乘积，单位运输成本为常数c，基准距离为D，售后修理部到再制造工厂的距离为Lj，j＝1，2，…，l，则运输成本为：

2 建立模型

汽车发动机再制造工厂的总成本函数是模型的目标函数，而总成本形式的设定参照文献［11］并进行扩展。依上述分析可知，汽车发动机再制造工厂的总成本由4个部分组成。

（1）汽车发动机再制造工厂从汽车4S店售后修理部回收数量为Sn的废旧汽车发动机的成本为

（3）汽车4S店售后修理部到汽车发动机再制造工厂的运输成本为Ct。

（4）再制造工厂回收的废旧汽车发动机数量与其需求量不能完全匹配引致的成本为Cm，即

由此得出汽车发动机再制造工厂总成本函数为：

（2）式约束条件为：

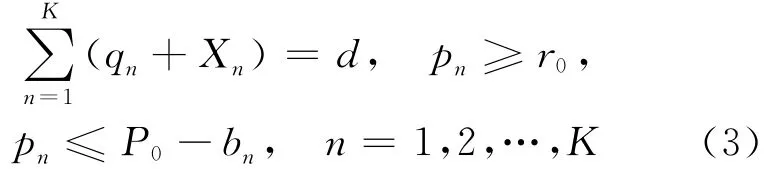
根据（2）式构造拉格朗日函数为：

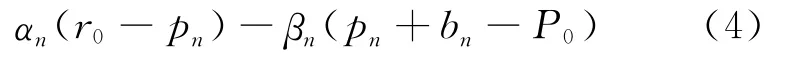
（4）式关于价格和数量的一阶库恩－塔克条件为：

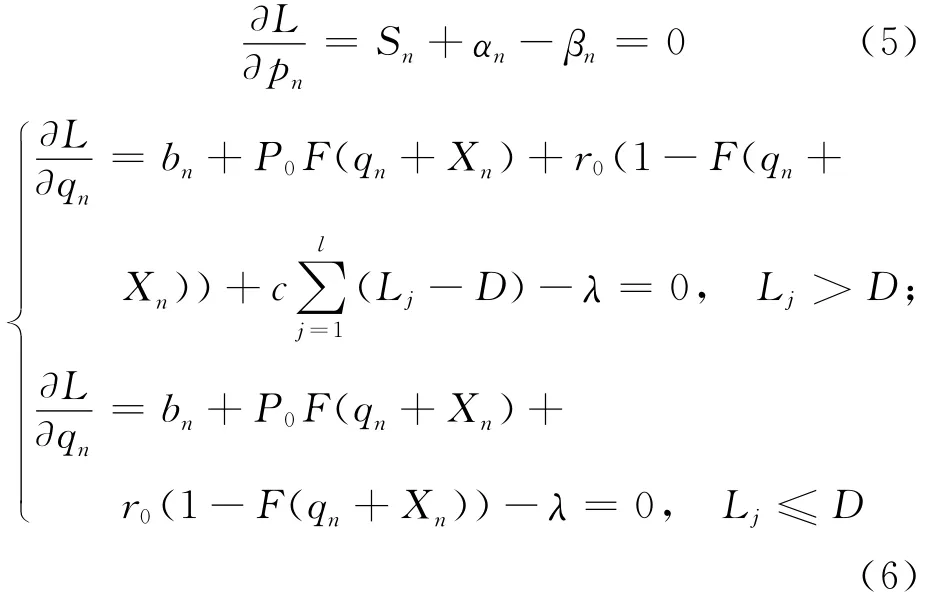
进一步得到互补松弛条件为：

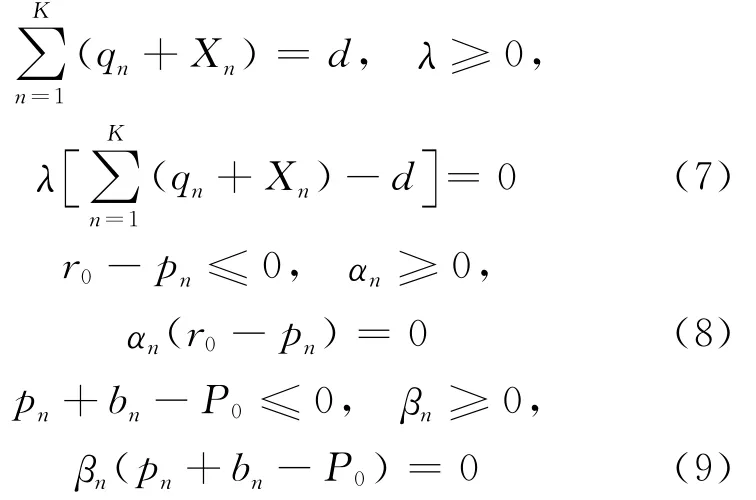
因此，由库恩－塔克条件得到汽车发动机再制造工厂从汽车4S店售后修理部回收废旧汽车发动机的最优数量qn，其必须同时满足下面2个方程：

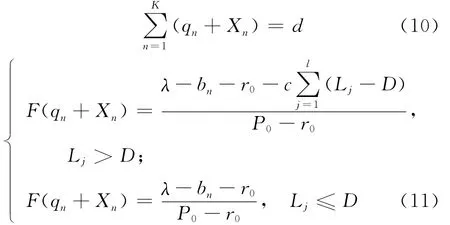
因概率F（qn＋Xn）既不能大于1，也不能小于0，所以限定条件为：

此外，参照文献［11］确定另一个均衡条件，即汽车发动机再制造工厂销售1台再制造汽车发动机的预期利润等于滞留1台再制造汽车发动机在工厂所带来的预期损失，即

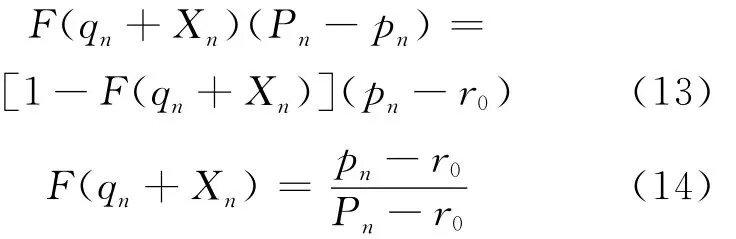
联合（11）式、（14）式得到汽车发动机再制造工厂向汽车4S店售后修理部提供回收废旧汽车发动机的最优价格以及最优数量。λ为调整废旧汽车发动机回收价格的关键变量，即

汽车发动机再制造厂根据自己对汽车4S店售后修理部向其提供废旧汽车发动机的数量预期，适时调整λ以达到调整回收价格的目的。

3 模型算法

从模型中解出再制造工厂的回收废旧汽车发动机的价格和数量最优值，步骤如下：

（1）获得r0、P0、Pn、bn、d、Xn、c、D、Lj值。

（2）由（15）式计算一组λ值；由（11）式计算所有关于n的F（qn＋Xn）。

（3）根据正态分布，已知均值μn和标准差σn，求出qn，即

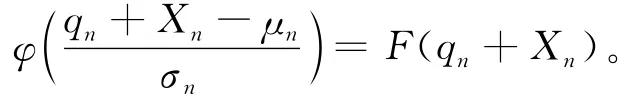
（5）根据步骤（4）再次计算F（qn＋Xn），然后再利用（14）式计算不同质量等级下废旧汽车发动机的回收价格pn。

4 算例分析

4.1 基本设置

为说明模型的求解过程和相关结论，给出如下数值算例。为简单起见，假设只有2个汽车4S店售后修理部，且与汽车发动机再制造工厂的距离不同，设L1＝58，L2＝45，D＝50，c＝0.5，n＝5，d＝2 000，r0＝20，P0＝80，Pn、bn、Xn为已知，见表1所列。

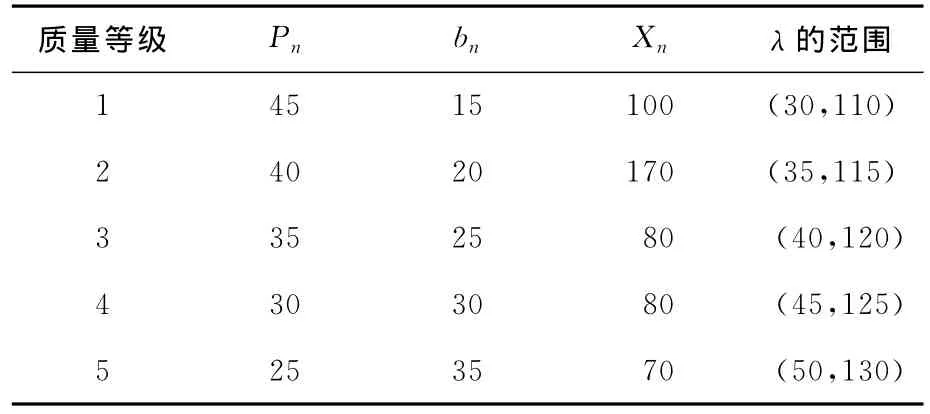
表1 不同质量等级下废旧汽车发动机回收再制造参数

由表1可知，质量等级越低的废旧汽车发动机在再制造过程中需要替换的零件就越多，再制造成本越高，且汽车4S店售后配件部可接受的再制造汽车发动机价格Pn就越低。

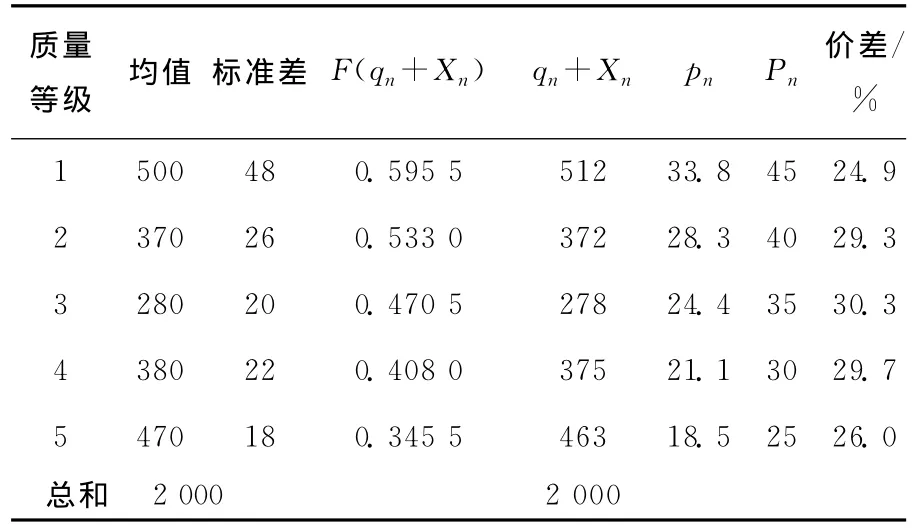
表2 λ＝77.64时不同质量等级下最优回收价格与数量

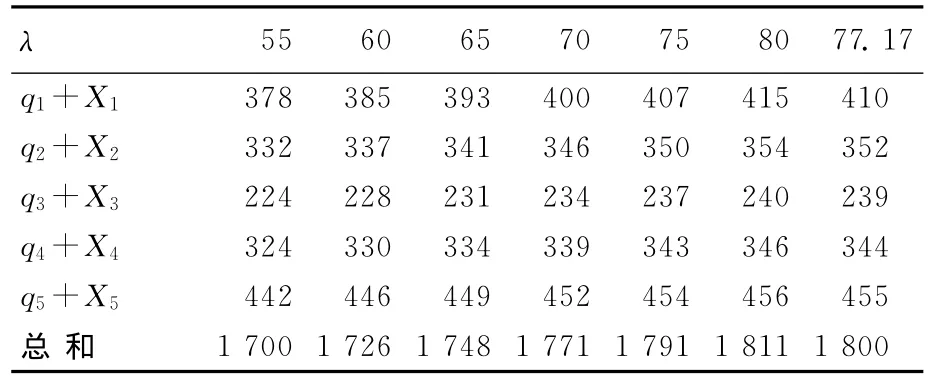
表3 不同λ值对应不同废旧汽车发动机回收数量

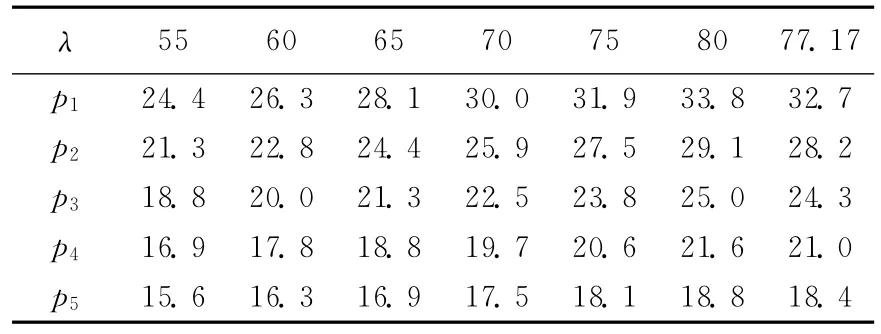
表4 不同λ值对应不同废旧汽车发动机回收价格

由表3、表4可知，随着λ值变大Xn）的值随之不断变大，最终使得d，汽车发动机再制造工厂回收废旧汽车发动机的价格pn也随之提高。这说明在废旧汽车发动机回收管理上采用最优价格能够有效平衡废旧汽车发动机的供给与对再制造汽车发动机的需求之间差距，同时也验证了模型算法步骤（4）所描述的规律具有合理性和现实意义。

5 结束语

本文建立了一个数量模型估计汽车发动机再制造工厂回收废旧汽车发动机的最优价格与最优数量，从而激励更多的废旧汽车发动机有效返回到汽车发动机再制造工厂进行再制造处理，且模型求解过程也表明在废旧汽车发动机回收管理上采用动态定价能够有效平衡废旧汽车发动机的供给与对再制造汽车发动机的需求之间差距。根据本文研究发现，推进我国汽车发动机绿色再制造业发展，就必须发展好汽车发动机回收再制造供应链中主体的合作关系，而建立并保持良好的供应链合作关系，实现合作企业的“多赢”局面，关键在于进行最优价格决策。

［1］ 许茂增，唐 飞.基于第三方回收的双渠道闭环供应链协调机 制 ［J］. 计 算 机 集 成 制 造 系 统，2013，19（8）：2083－2089.

［2］ 张成堂，杨善林.双渠道回收下闭环供应链的定价与协调策略［J］.计算机集成制造系统，2013，19（7）：1676－1683.

［3］ Reverse logistics：quantitative models for closed－loop supply chains［M］.Springer，2004：3－27.

［4］ Karakayali I，Emir－Farinas H，Akcali E.An analysis of decentralized collection and processing of end－of－life products［J］.Journal of Operations Management，2007，25（6）：1161－1183.

［5］ 孙晓晨，涂菶生.产品回收系统最优静态定价策略［J］.南开大学学报：自然科学版，2007，40（2）：20－25.

［6］ 孙 浩，达庆利.随机回收和有限能力下逆向供应链定价及协调［J］.系统工程学报，2009，23（6）：720－726.

［7］ 王玉燕，李帮义，申 亮.供应链、逆向供应链系统的定价策略模型 ［J］.中国管理科学，2006，14（4）：40－45.

［8］ 杨爱峰，王 晓.基于回收价格的再制造系统策略研究［J］.合肥工业大学学报：自然科学版，2011，34（4）：593－597，608.

［9］ Guide V D R，Teunter R，Van Wassenhove LVN.Matching demand and supply to maximize profits from remanufacturing［J］.Manufacturing ＆ Service Operations Management，2003，5（4）：303－316.

［10］ 李 响，李勇建.随机环境下考虑回收定价和销售定价的逆向供应链优化与协调研究［J］.系统科学与数学，2012，31（11）：1511－1523.

［11］ Pokharel S，Liang Y.A model to evaluate acquisition price and quantity of used products for remanufacturing［J］.International Journal of Production Economics，2012，138（1）：170－176.