基于多阶抽样的林地蓄积量估测方法1)——以三峡库区为例
2015-03-06李云霄彭道黎何彦然黄国胜王雪军
李云霄 彭道黎 何彦然 黄国胜 王雪军
(北京林业大学,北京,100083) (国家林业局调查规划设计院)
责任编辑:王广建。
森林调查是获取森林资源信息和分析决策的一项基础性工作。为了获得森林资源的数据,通常使用的方法是全林调查法,这种方法不但费时费力,而且成本高。随着统计学的发展,抽样调查方法,在林地资源监测、分析与评价领域得到广泛运用。
抽样技术和实地调查是两种重要的信息获取方式。抽样技术是一种非全面的调查手段,通过不同抽样方法选取样本(即以样木、样地等为抽样单元进行调查),并根据相应算法估测森林资源总体数量。多阶抽样是根据实际情况,将整个抽样程序分成若干个阶段进行抽样。多阶抽样有利于抽样调查的组织实施、降低调查成本以及满足各级部门对调查资料的需求[1]。
目前,抽样调查技术在林业、地质、渔业、生态环境保护以及农业统计等领域应用日益广泛。在国外,T.Charles等[2]采用抽样方法对林地资源量变化进行有效估计,并对林地资源量的动态变化进行监测;美国的森林资源清查与分析,采用三阶抽样与遥感影像及实地调查相结合的设计[3];加拿大的国家森林资源清查采用统一的抽样格网,根据生态区进行分层,利用遥感资料、森林经营档案和其他辅助信息源,在遥感判读样地中选取1个或多个多边形进行地面抽样调查,构成两阶成团抽样设计[4];澳大利亚则提出了基于多阶抽样设计的全国森林资源监测体系框架[5]。在国内,朱维凡[6]探讨了PR抽样设计,估计蓄积量的方法,PR抽样是一阶单元采取不等概率抽样,二阶单元采取等概率的抽样;章礼拐等[7]将遥感图像处理技术与分层抽样相结合,调查精度达到国家规定要求,节省了调查成本。1977年,我国建立的全国森林资源连续清查体系,采用以千米网交叉点作为样点定位的系统抽样方法。重庆市采用4 km×4 km抽样间隔对林地蓄积量进行调查;湖北省采用4 km×8 km抽样间隔对林地蓄积量进行调查,先在1∶50 000地形图上布设样点,每隔5年,对样地重复测量一次,用以推算全省森林资源现状及消长变化。
综上所述,利用多阶抽样与实地调查相结合的方法仍然较少。本文主要通过三阶抽样技术与实地调查相结合,对三峡库区的林地蓄积量进行估测,并通过对其总体精度的分析,证明此方法的可行性。
1 研究区概况
长江三峡库区位于(东经105°50'~111°40'、北纬28°31'~31°44')四川盆地与长江中下游平原的结合部。跨越鄂中山区峡谷及川东岭谷地带,北屏大巴山、南依川鄂高原,包括湖北省西部四县、重庆市22个区县,全长660 km,总面积5.8万km2。库区属于亚热带季风气候,年降水量1 000~1 800 mm,分布均匀。在第七次清查中,库区森林覆盖率达到39.56%,第八次清查中达到45.74%。
2 研究方法
2.1 数据来源
以三峡库区边界图(见图1)、三峡库区各县行政边界图,三峡库区二类调查数据作为实验数据。首先,将三峡库区边界图进行多阶抽样方案设计。最后,对三阶抽样结果进行统计分析及计算,估测得到三峡库区林地蓄积量,并与由一类清查数据统计得到的三峡库区林地蓄积量、二类调查统计得到的三峡库区林地蓄积量进行比较,分析其总体精度。
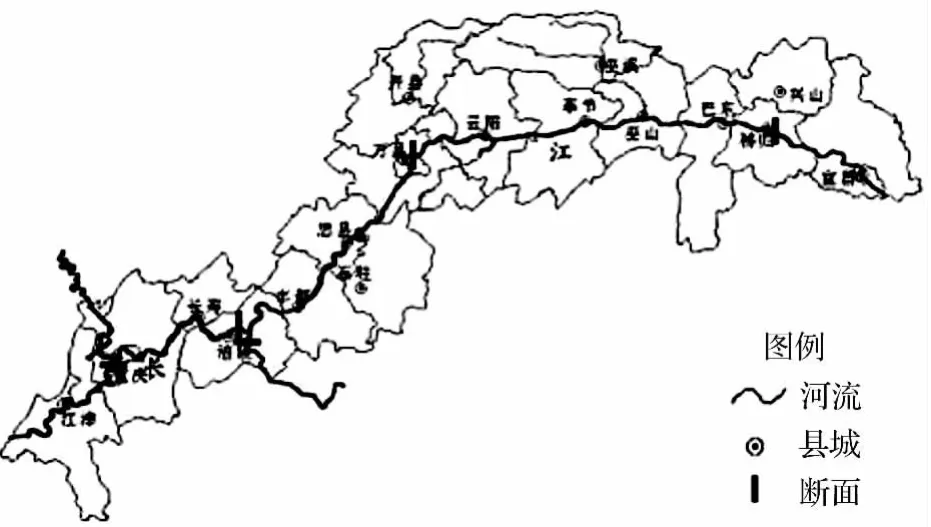
图1 三峡边界图
2.2 抽样设计
一阶抽样设计:加拿大的国家林地资源清查(NFI)全国采用20 km×20 km格网进行抽样,各省可以根据需要进行加密;澳大利亚的林地资源清查设计网格,按照20 km×20 km;巴西按20 km×20 km网格布设样地。世界上较多国家采用20 km×20 km网格进行布设抽样,所以本方案一阶样地大小采用20 km×20 km。
对三峡库区边界图进行网格划分,生成218个20 km×20 km的格网,去掉边界面积小于50%的网格,最终剩余146个20 km×20 km的格网(如图2)。
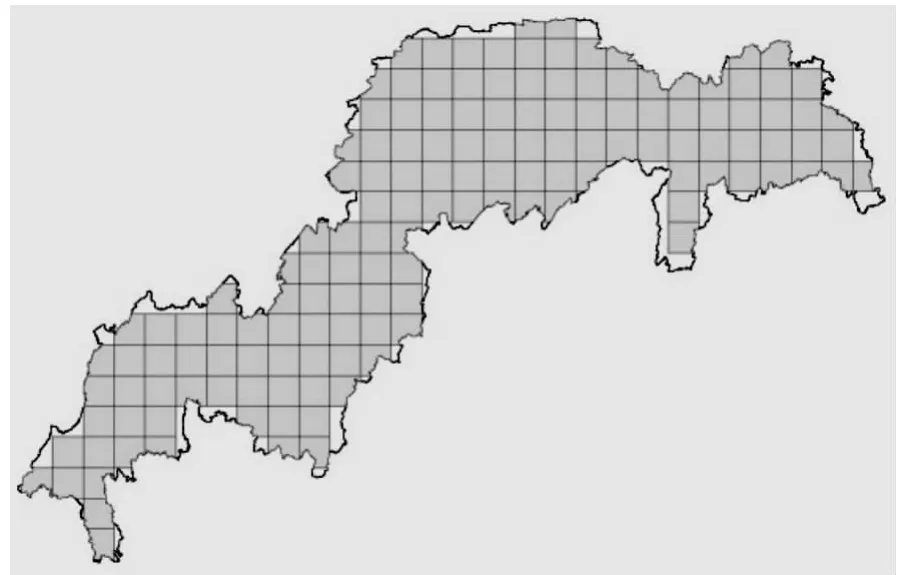
图2 一阶网格布设图
二阶抽样设计:对三峡库区不同大小的样地进行模拟试验并计算其变动系数。试验样地大小分别为1 km×1 km、2 km×2 km、3 km×3 km、4 km×4 km、5 km×5 km、6 km×6 km、7 km×7 km、8 km×8 km、9 km×9 km、10 km×10 km,计算样地的变动系数、抽样框个数及抽样间距,并分析不同大小样地变动系数的变化趋势。
林地变动系数计算公式如下:

式中:n为总体内网格数,yi为第i个网格的林地面积为三峡库区每阶样地总体的平均林地面积。
一阶样地样本单元个数:

式中:A为总体面积,a为样本单元面积,t为可靠性指标(按95%可靠性),C为总体变动系数,E为相对误差。
二阶抽样单元个数:
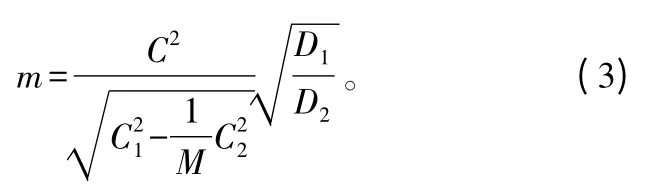
式中:m为二阶抽样单元个数,C1为一阶变动系数,C2为二阶变动系数,D1为调查一个一阶样本单元所需的平均成本,D2为调查一个二阶样本单元所需的平均成本。
三阶抽样设计:三阶样地即为实地调查样地,根据实际情况,大样地实地调查通常选用100 m×100 m,所以三阶样地大小确定为100 m×100 m。
2.3 蓄积量估测
对三阶样地进行实地调查,统计得到三阶样地蓄积。对三阶样地实地监测到的活立木蓄积量进行统计,计算得到所有三阶样地的活立木总蓄积量,并通过以下4种方式推测二阶样地、一阶样地及三峡库区总蓄积量。
逐级比例反推:V二阶=V三阶/f3;V一阶=V二阶/f2;V三阶=V一阶/f1。
跨级比例反推:V三峡=((V一阶/f1)/f2)/f3。
逐级面积反推:V二阶=V三阶/f6;V一阶=V二阶/f5;V三峡=V一阶/f4。
跨级面积反推:V三峡=((V一阶/f4)/f5)/f6。
式中:f1是一阶抽样比例,f2是二阶抽样比例,f3是三阶抽样比例,f4是一阶抽样面积比例,f5是二阶抽样面积比例,f6是三阶抽样面积比例。
2.4 估计值方差及精度计算
三阶抽样关系比较复杂,设yiju表示总体中第i个一阶样本单元中第j个二阶样本单元内的第u个三阶样本单元的标志值。在各阶等概抽样条件下,求出各阶相应的样本平均数。
第i个一阶样本单元中第j个二阶样本单元内的第u个三阶样本单元平均数为:

第i个一阶样本单元中第j个二阶样本单元平均数为:

则总体三阶单元平均数估计值(三阶样本单元平均数)为:

t值使用危险率a=1,自由度df=n-1,查小样本t分布表。
估计精度:PC=1-E。
3 结果与分析
3.1 一阶、二阶样地变动系数及样本单元数
根据公式1及二类调查数据计算样地得一阶变动系数(C1=0.2880),通过公式(2)计算得到一阶样地样本单元数及各样本单元格间距(n=26)。为保证调查精度,在确定的样本单元数上增加10%~20%的安全系数。则n=30。则布点间距d=(A/n)1/2=43 084.78 m。去除边界面积小于50%的跨界样地,所以经过试验确定布点间距为40 500 m。在边界图上进行均匀布点,以点为中心,向外扩生成20 km×20 km网格(如图3),即为一阶抽样样地共30个。
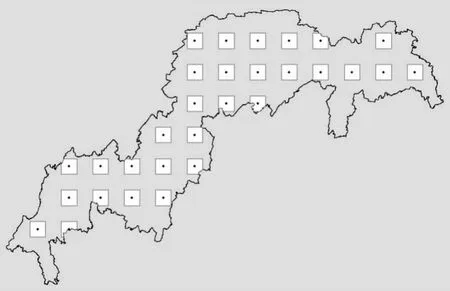
图3 一阶抽样样地分布图
对三峡库区不同大小的样地进行模拟试验,计算其变动系数、抽样框个数及抽样间距(见表1)。由表1可知,当样地大小为4 km×4 km时,变动系数趋于稳定。故二阶样地大小确定为4 km×4 km。
在一阶样地内布设4 km×4 km的二阶样地共743个,去掉边界面积小于50%的跨界样地,最终剩余731个二阶样地(见图4)。

表1 三峡林地变动系数表
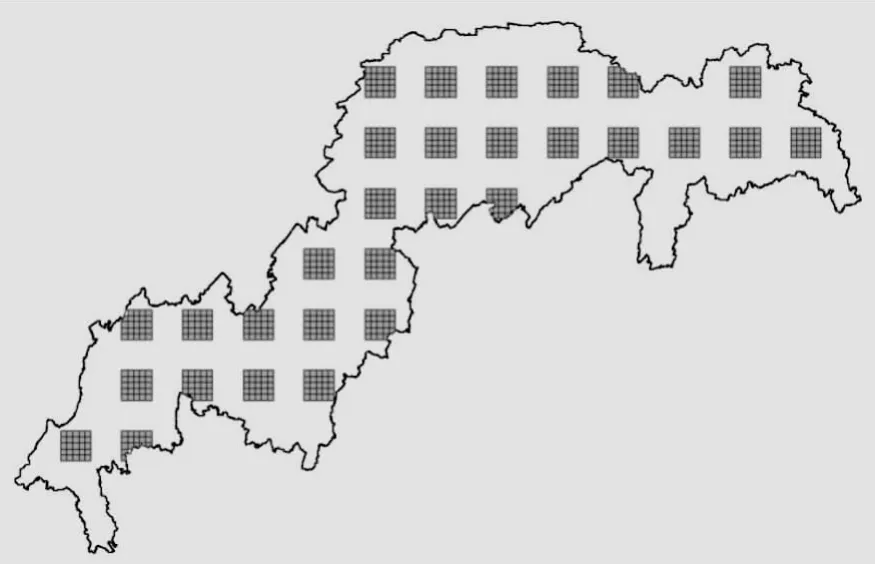
图4 二阶网格布设图
同样,利用公式(1)及二类数据,计算其变动系数(C2=0.314 7)。则通过公式(3)计算得到二阶抽样单元个数(m)为6个。为保证调查精度,在确定的样本单元数上增加10%~20%的安全系数,则二阶抽样单元个数取7个。则布点间距d=(A/n)1/2=7 559.289 m。去除边界面积小于50%的跨界样地,经过试验确定布点间距为6 750 m。总共需抽取206个二阶样地。
在边界图上进行均匀布点(见图5),以点为中心,向外扩生成4 km×4 km网格,去除边界面积小于50%的跨界样地,剩余206个样地即为二阶抽样样地。

图5 二阶抽样样地分布图
3.2 三阶抽样设计
三阶样地即为实地调查样地,根据实际情况,大样地实地调查通常选用100 m×100 m,所以三阶样地大小确定为100 m×100 m。在二阶样地内布设100 m×100 m的三阶样地,去掉边界面积小于50%的跨界样地。
同样,利用公式(1)及二类数据计算其变动系数C3=0.585。三阶抽样单元个数确定与二阶抽样单元个数确定方法一样,则计算得到三阶抽样的个数(g)为74。为保证调查精度,在确定的样本单元数上增加10%~20%的安全系数。则三阶抽样的个数取90个。则布点间距d=(A/n)1/2=421.637 m。去除边界面积小于50%的跨界样地,所以经过试验确定布点间距为375 m。每个二阶样地里面抽取116个三阶样地。在边界图上进行均匀布点(见图6),以点为中心,向外扩生成100 m×100 m网格,即为三阶抽样样地共计33 571个。
图6 三阶抽样样地分布图
3.3 蓄积量估测及检验
各阶抽样比例为:
f1=i/n=0.21;f2=j/m=0.28;f3=u/g=23754/327752=0.07;f4=A一阶/A三峡=0.20;f5=A二阶/A一阶=0.28;f6=A三阶/A二阶=0.07。
对三阶样地进行实地调查,统计得到三阶样地蓄积并通过以下4种方式推测二阶样地、一阶样地及三峡库区总蓄积量。计算结果见表2。

表2 总体蓄积推算值及总体精度表
根据表2可知,利用三阶抽样技术与实地调查相结合的方法,对三峡库区林地总蓄积量进行了较为准确的估测。且利用逐级比例反推和跨级比例反推得到的结果基本一致,逐级面积反推与跨级面积反推得到的结果也基本一致。与一类清查结果比较,利用抽样比例反推的总体精度明显高于利用面积比例反推的总体精度;与二类调查结果比较,利用抽样比例反推得到的总体精度明显低于利用面积比例反推总体精度。同时,与一类清查数据统计的三峡库区活立木总蓄积进行蓄积误差比较分析,总体精度最高达到99.52%,对应得出三峡库区林地总蓄积量为13 9738 605.8 m3,与二类数据统计的三峡库区活立木总蓄积进行蓄积误差比较分析,总体精度最高达到94.19%,对应得出三峡库区林地总蓄积量为142 068 794.1 m3。两种对比的总体精度都较高,达到了90%以上,说明利用三阶抽样方法估测林地蓄积量是可行的。
对三阶抽样结果进行检验,根据三阶抽样方差,计算得到总体方差、标准误、估计误差限及估计精度等指标。在α=0.1的情况下,估计精度达到87.16%,基本达到精度要求,同样说明利用三阶抽样方法估测林地蓄积量是可行的。
4 结论与讨论
利用三阶抽样技术与实地调查相结合的方法为准确估测大尺度范围的林地蓄积量提供了一种有效的途径。虽然用此方法估测得到的林地蓄积量,与实际三峡库区林地蓄积量比较的总体精度最高达到99.53%,且估计精度同时达到87.16%,均达到精度要求。但是三阶样地即实地调查监测样地个数达到23 754个,个数较多。造成三阶实地调查样地较多的原因,第一种可能的原因是在计算变动系数时,选用的计算标准为林地面积,,进而求算样本单元个数不具代表性。可以在今后的试验中,改变计算变动系数的标准,采用单位面积蓄积代替林地面积,可能对于样地个数的确定更具代表性。第二种可能的原因是整个三峡库区的林地蓄积变动较大,导致求算样本单元数较大,可以在今后的试验中,先对三峡库区进行分层,然后在每一层再进行多阶抽样,这样就可以大大减少三阶样本的个数。第三种可能的原因是三阶样地大小不合适,因为样地面积大小的选定直接影响在一定精度要求下的样地数量。在后续的研究中,应该对此方法进行改进,使其不仅可以在较高精度下估测总体蓄积量,还可以在保证精度的情况下估测各个县的蓄积量。
[1]林昌庚.森林资源清查[M].沙琢,译.北京:中国林业出版社,1985.
[2]Charles T Scott.Sampling Method for Estimating Change in Forest Resources[J].Ecological Application,1998,8(2):228-233.
[3]叶荣华.美国国家森林资源清查体系的新设计[J].林业资源管理,2003(3):65-68.
[4]Mark D.Gillis.Canada's National Forest Inventory(Responding to Current Information Needs)[J].Environmental Monitoring and Assessment.2001,67(1/2):121-129.
[5]曾伟生,程志楚,夏朝宗.一种衔接森林资源一类清查和二类调查的新方案[J].中南林业调查规划,2012,31(3):1-4.
[6]朱维凡,韦希勤.PR抽样在森林蓄积量调查中的应用[J].内蒙古林业调查设计,1999(1):26-27.
[7]章礼拐,汪乃武,魏志刚,等.利用TM图像进行二类调查中的分层抽样技术[J].安徽林业科技,2000(2):1-3.
