基于修正函数的杉木人工林单木冠幅预测模型1)

董晨 吴保国 韩焱云 刘建成

(北京林业大学，北京，100083)

责任编辑:王广建。

树冠是林木进行光合作用的主要场所。树冠的大小成为衡量林木生长健康与否的重要指标，反映树冠大小的指标非常多，最常用的指标仍然是冠幅［1］。冠幅模型是建立树冠冠幅与冠长、枝下高等树冠属性及林分其他因子之间关系的函数。国内外学者对单木冠幅模型已有大量研究，构建单木冠幅模型的方法很多，其中以线性回归模型居多。Curtis等［2］首次用线性回归法，构建了以直径、树高和立地等级为变量的黄衫冠幅生长模型，线性回归法在冠幅模型的构建上得到了广泛的应用［3－4］。在我国，雷相东等［5］构建了长白落叶松等9个树种的冠幅多元回归模型;周元满等［6］建立了桉树冠幅阶跃函数模型，该模型较好地解决分段拟合模型在变点上的不连续问题，其应用效果优于一般回归模型;刘平等［7］采用一元和多元线性回归法构建低山侧柏的单木冠幅模型;覃阳平等［8］建立了与距离有关的竞争指数、树高和胸径的冠幅线性回归模型。采用线性回归法构建模型虽然计算简便，但假设条件多、自变量之间存在共线性及异相关等局限性［9］。相比之下，非线性模型由于其变量组合形式的多样化，在模型的表达上具有更大的探索空间。近年来，研究者更多地运用非线性回归方法构建冠幅模型，如Ritchie等［10］采用非线性三阶段最小二乘法构建幼龄黄衫的冠幅生长方程，模型表达了冠幅增长量与冠幅面积和树高增长的关系;Ledermann［11］构建了云杉的非线性冠幅枯损模型;符利勇等［12］以立地指数和样地因子作为水平因子，建立了非线性混合单木冠幅模型。若采用单一的非线性理论或经验方程进行方程拟合，模型自变量选取复杂;混合模型尽管可以自由选择自变量，模型精度较高，但模型的构建过程复杂。

在诸多的非线性回归方程中，修正方程以修正变量和基础模型组合的形式存在，基础模型根据因变量的属性而制定，修正变量的加入能够尽量缩小理论模型与实际结构之间的误差，且修正模型直观易懂，应用方便。本文以冠幅的潜在生长量为基础模型，以林分密度、地位指数、林木竞争指数及林木直径为修正变量，构建杉木人工林单木冠幅模型，并与线性回归模型的拟合优度进行对比分析。

1 研究区概况

顺昌县位于福建省的西北部，地理坐标为117°30'～118°14'E，2635'～27゜12'N。该地区属中亚热带海洋性季风气候，年平均气温为18．9℃，1月平均气温为7．8℃，7月平均气温为28．1℃。地形以低山丘陵为主，海拔300～500 m。气候温和，雨量充沛，年降水量1 600～1 800 mm。土壤深厚、湿润、肥沃。森林覆盖率75．6%，属于福建省重点林区。主要用材树种有:杉木(Cunninghamia lanceolata)、马尾松(Pinus massoniana)、黄山松(Pinus taiwanensis Hayata)、巨尾桉(Eucalyptus grandis)、柳杉(Cryptomeria fortunei Hooibrenk)、侧柏(Platycladus orientalis)、刺槐(Robinia pseudoacacia)、毛竹(Phyllostachys heterocycla)、银桦(Grevillea robusta)等。

2 材料与方法

2．1 数据来源

实验地点设置于福建省顺昌县岚下乡林场。根据不同林龄和密度选取50块大小为30 m×30 m杉木人工纯林样地，使用围尺和激光测高仪分别测量样地中每株树木的胸径(D)和树高(H);在每块样地选择5～7株树冠生长较对称的林木作为标准木，选择2～3株树高长势良好，并且与周围树木竞争较小的林木作为优势木，借助皮尺和塔尺分别测量标准木和优势木的东西冠幅和南北冠幅。胸径测量的精度为0．1 cm，其他变量的精度为0．1 m，将东西冠幅和南北冠幅的平均数作为冠幅数据。同时记录每块样地的平均胸径、平均树高和林分密度。所采集的数据中，根据不同树龄、密度及立地条件，选择其中的227株杉木数据用于模型拟合，78株用于模型检验。模型拟合和检验的数据汇总见表1。

表1 模型拟合与检验数据汇总

2．2 研究方法

树冠的生长与林木直径生长类似，在周围没有竞争的前提下，树冠能够在林木生理所限定的范围内自由生长。但林分内绝大多数林木，由于林木间的相互竞争，林木的实际生长量小于潜在生长量，减小的程度与林分密度及林木之间的竞争程度有关;同时，树冠的生长还与立地条件以及其他林分因子相关。本研究以冠幅各个方向长度一致为假设前提，以反映冠幅潜在生长的冠幅－树龄函数作为基础模型，以胸径生长函数、地位指数、林分密度及竞争指数作为修正变量，对模型进行修正。杉木人工林单木冠幅表达式为:

其中:CW代表冠幅，F(CW0)代表树冠潜在生长方程，YCW代表误差函数，φ1、φ2、φ3、…分别代表修正变量。

在模型的拟合中，根据决定系数(R2)最大和均方残差(MSE)最小来判断最优的拟合函数。

在评价方程的拟合效果时，采用平均系统误差(B)、均方根误差(RMSE)和相对均方根误差(RRMSE)指标来检验拟合效果，各项检验指标如公式3～5所示。此外，在数据拟合之前，使用箱形图剔除两倍标准差之外的异常数据。

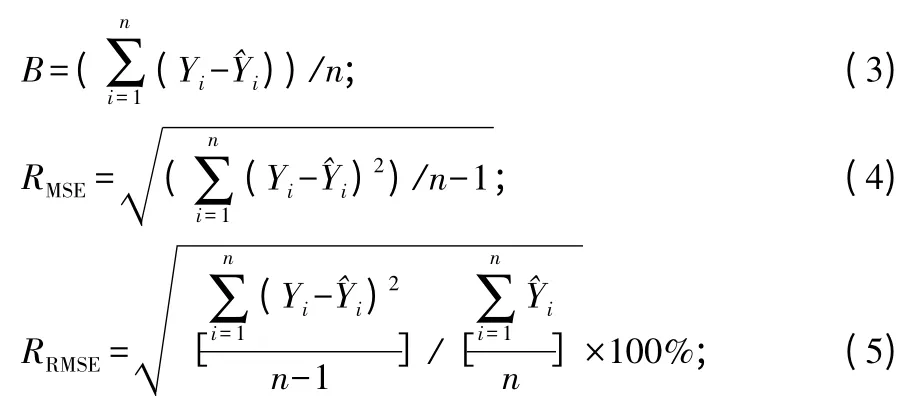
其中:n为样本数，Yi为参与检验的冠幅实际值，Yi为冠幅预测值。

3 结果与分析

3．1 冠幅潜在生长方程

由于实际调查中的疏开木不易确定，因此，在本研究中，以优势木的冠幅生长过程代替疏开木的生长过程，采用最常见的7个经验方程以及Logistic、Mitscherlich、Comperts、Korf和Richards五个理论方程对36块样地的108株不同树龄、冠幅长势良好的优势木进行拟合，建立冠幅－树龄的函数(见表2)。

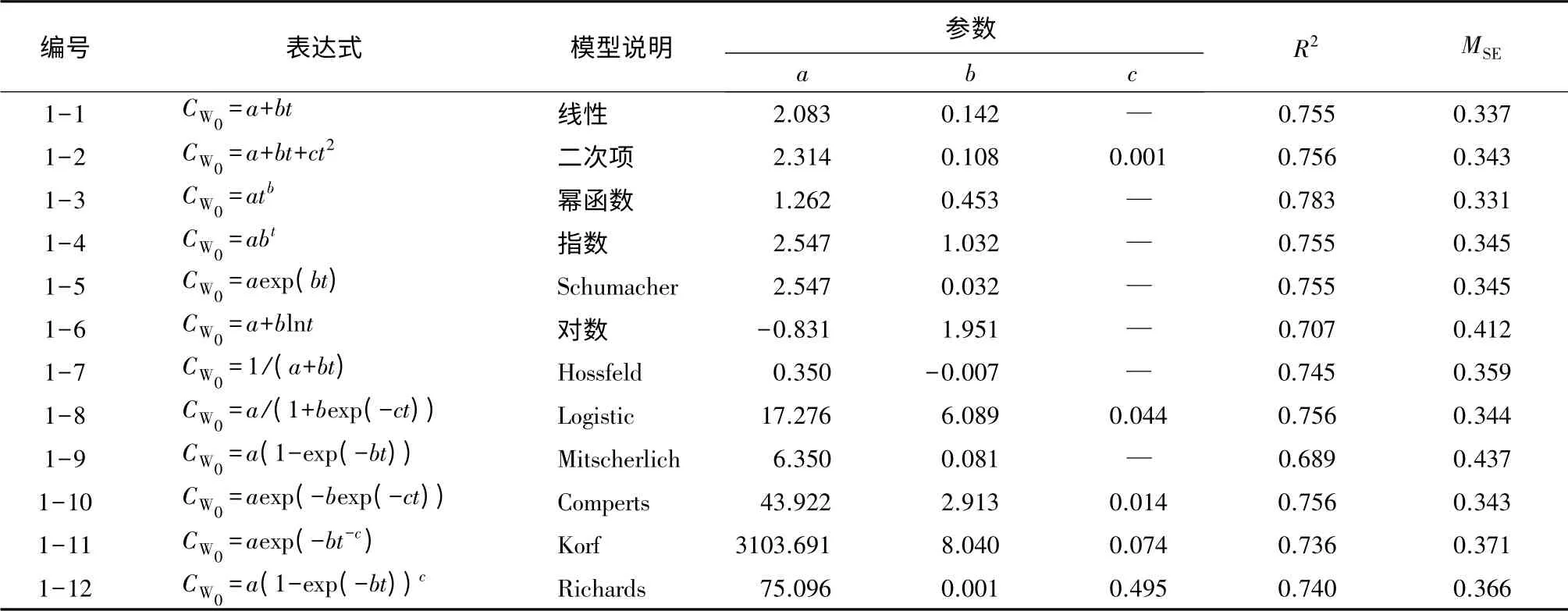
表2 冠幅潜在生长方程拟合结果

在显著性检验统计量F的sig值均小于0．05的前提下，在12个模型中，得到幂函数的相关系数R2最大(0．783)，均方残差最小(0．331)。因此，采用幂函数作为修正函数的基础模型。

3．2 修正函数的建立

建立修正函数首先要选择修正变量来构造误差函数，研究中以地位指数、林分密度、竞争指数和直径作为修正变量。

地位指数。立地条件对林分的生长收获具有重要的影响，通常采用地位指数或者地位级来判断林地的立地条件。对于人工林而言，林地会受到间伐、补植等人为因素的干扰，林分条件平均高会因此受影响，从而影响有林地立地条件的判断。而优势木的生长受人为干扰因素较少，因此，本研究选择地位指数作为立地条件的判定指标。

构建有林地地位指数的方法有导向曲线法、代数差分法，广义代数差分法等［13］，本研究使用代数差分法构建地位指数模型。选择Richards、Mitscherlich、Korf、Logistic和Compertz 5类理论生长方程作为基础模型，对于各类曲线中的参数a、b、c，以参数b作为消元参数，保留参数a、c。差分消元后，得到5个2参数的差分方程。采用研究区的每个样地平均优势木－树龄数据，平均分成两组进行方程拟合，选择其中一组数据，将其优势木的树高作为地位指数，树龄为杉木基准树龄20。

研究采用SPSS17．0，选取50块样地中的100株优势木作为研究对象，经拟合和检验，发现由Richards方程转化而成的差分方程，在众模型中得到的决定系数最高、均方残差最小。其具体的模型表达如公式7所示。

其中，IS为地位指数;t为任意时刻的优势木树龄;H为树龄t时对应的优势木高。

林分密度。树冠的生长与密度息息相关，衡量林分密度的指标很多，从便于林业生产实际应用出发，拟从每公顷株数(N)和相对植距(RS)两个林分密度测度中，选择一个与冠幅生长关系最为密切的指标作为林分密度指标。相对植距的是林分中林木的空间的开方与优势木高的除数。

其中:N为林分的密度;H0为优势木高。

在N和RS两个变量中，分别对其与冠幅数值进行Pearson相关性分析，挑选出相关系数最大的变量作为密度修正变量。由表3可知，N与冠幅的相关系数为－0．745，大于RS与冠幅的相关系数，因此，将N作为密度修正变量。

竞争指数。林分密度只能反映林分内每株林木平均占有的空间，但未考虑不同大小的林木占有不同的空间，而导致林木间的竞争关系也不同的问题［14］，冠幅的生长也受到竞争指数的影响。一个好的竞争指数，不仅应与林木生长关系密切，有一定的理论依据，还应该形式简单直观，测算容易，应用方便［15］。在实际操作中，由于与距离有关的竞争指数测量困难且计算复杂，研究表明，与距离无关的竞争指数，在方程的拟合中，优度不亚于前者［16－17］。根据上述原则，本文选择相对直径、相对树高和树高直径比作为与距离无关的单木竞争指标，3个指标的具体表达可见公式(9)～(11)。

其中:RDi为相对直径;RHi为相对树高;RHDi为树高直径比;di为林分中各林木的胸径;hi为林分中各林木的树高;H0为林分优势木高;Dg为断面积平均胸径;Di为单株木相对直径竞争水平。

分别对各指标与冠幅数值进行Pearson相关性分析，挑选出相关系数最大的变量作为竞争指数修正变量。由表3得RD与冠幅的相关系数最大，为0．790，故将RD作为竞争指数的修正变量。

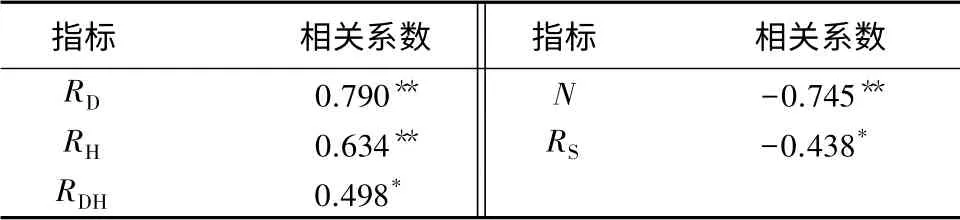
表3 各指标与冠幅的Pearson相关性

其他修正变量。除了地位指数、林分密度及竞争指数以外，冠幅的生长还受林分因子的影响。利用多元线性回归中的逐步回归法剔除变量，其原理是当一个变量的F统计量概率双侧检验的显著性水平≤0．05时，则引入该变量;当显著性水平≥0．10时，则剔除变量。为消除共线性，病态指数大于15或者容许度小于0．5的变量也排除在外。对37块样地的227株的杉木数据(胸径、树高、枝下高、树冠比)进行逐步回归分析，按照上述原则，被纳入的变量有地位指数、林分密度、竞争指数及胸径被选入作为修正变量。

根据不同形式的理论和经验方程，对227株杉木的胸径数据进行拟合，得到决定系数R2最高的方程。

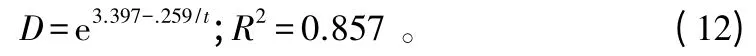
其中:D为平均胸径;t为林龄。

修正变量构造的误差函数YCW应该满足以下性质:

随着IS的增加，单株树木的优势木越高，树木长势越好，CW会随之增加，修正函数CW为IS的增函数;林分密度越高，树木竞争越激烈，冠幅生长受阻，因此，密度是CW的减函数;竞争指数越高，单木较平均木而言长势良好，相应的生长空间越大，CW为RD的增函数;林木直径与冠幅呈现显著的正相关性，CW为直径的增函数。

相关文献［15，18］表明，误差函数的构建方式以指数函数和幂函数的组合形式为最佳，因此，研究选择通过指数函数和幂函数来组合误差变量。每个修正变量都有两种表达形式，4个变量的误差函数则有16种表现方式。

结合已建立的冠幅潜在生长量函数，采用SPSS17．0，对37块样地的227株的杉木数据进行拟合，每类组合下的模型拟合结果见表4。由表4可知，1号组合的模型拟合效果最佳，其中系数α1=0．568，α2=－0．228，α3=1．085，α4=0．093，决定系数R2=0．876，MSE=0．081。则:

结合误差函数，根据冠幅模型的表达式CW=CW0×YCW，即得出单木冠幅预测模型。

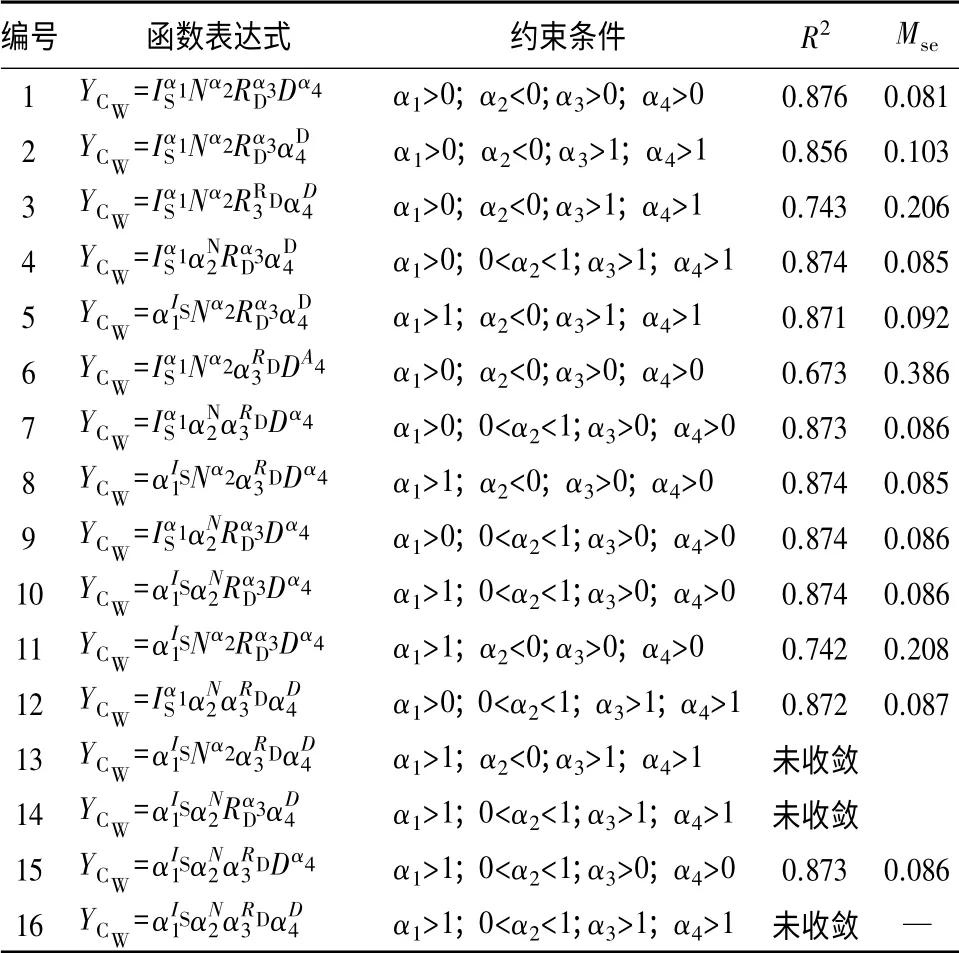
表4 误差函数表达式

3．3 模型检验

根据所拟合的冠幅修正模型，对未参与建模的13块样地中的78株杉木数据进行计算，经数据的整理和计算，在F双侧检验显著水平P＜0．05的前提下，得到B=0．053，RMSE=0．241，RRMSE=12．0%，模型的预测误差较小，因此，模型有一定的实用性。

为了进一步验证模型的真实性，分别对三个模型进行残差分析，分析结果如图1所示。

图中横坐标为冠幅值，纵坐标为各个模型的标准化残差值，由图1可知，一元线性回归的残差有小部分值超出［－2，2］的区间，且对于误差项方差为0的假设，其残差分布与正态分布稍微有所偏差;多元线性回归方程的残差分布尽管符合正态分布，但仍有部分残差值小于－2;而修正模型的残差分布既符合回归分布原则，其残差值都在［－2，2］的区间，残差值更加紧凑。因此，进而说明采用修正模型拟合杉木的单木冠幅具有优越性。

图1 模型残差分布

4 结论与讨论

在构建树冠单木模型时，多数使用的是一元模型或多元线性回归模型［19－21］。而本研究中采用修正法拟合的模型的决定系数为0．876，说明修正模型与线性模型相比，在精度上大大提高。

修正模型的构建中，修正变量的选择十分重要。根据经验以及数据的相关性分析，发现冠幅的生长与林分密度、地位指数、竞争指数和胸径呈现明显的相关性，因此，选择上述指标作为修正变量。但是不同树种存在不一致的生长特性，或者同一树种在不同的环境下，会获得不同的量测数据，从而导致冠幅生长与林分因子相关性的不一致，因此，修正变量的选择要根据数据的实际情况考虑。

本研究所构建的修正模型，尽管在精度上较线性回归模型有所提高。考虑到模型的推广应用，虽然树高、枝下高、冠长比等因子与冠幅也存在显著的相关性，但未将其作为修正因子，也未考虑经营作业对树冠生长的影响。因此，如何综合与冠幅生长相关的各种因子，构造更准确的冠幅模型，仍需要进一步的研究。

［1］Miguel G C，Martin E A，Ronald H W．Development and testing of models for predicting crown fire rate of spread in conifer forest stands［J］．Canadian Journal of Forest Research，2005，35(7):1626－1639．

［2］Curtis R O，Reukema D L．Crown development and site estimates in a Douglas-fir plantation spacing test［J］．Forest Science，1970，16(3):287－301．

［3］Bechtold W A．Largest crown-width prediction models for 53 species in the western United States［J］．Western Journal of Applied Forestry，2004，19(4):245－251．

［4］Russell M B，Weiskittel A R．Maximum and largest crown width equations for 15 tree species in Maine［J］．North JAppl For，2011，28(2):84－91．

［5］雷相东，张则路，陈晓光．长白落叶松等几个树种冠幅预测模型的研究［J］．北京林业大学学报，2006，28(6):75－79．

［6］周元满，谢正生，刘素青，等．短轮伐期桉树林分树冠生长的阶跃函数模型［J］．南京林业大学学报:自然科学版，2006，30(2):59－62．

［7］刘平，王玉涛，马履一．低山侧柏人工林单木冠幅预测模型及精度评价［J］．林业资源管理，2014(2):52－58．

［8］覃阳平，张怀清，陈永富，等．基于简单竞争指数的杉木人工林树冠形状模拟［J］．林业科学研究，2014，27(3):363－366．

［9］Uzoh F CC，Oliver WW．Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model［J］．Forest Ecology and Management，2008，256(3):438－445．

［10］Ritchie M W，Hamann J D．Individual-tree height-，diameterand crown-width increment equations for young Douglas-fir plantations［J］．New Forests，2008，35(3):173－186．

［11］Ledermann T．A non-linear model to predict crown recession of Norway spruce(Picea abies［L．］Karst．)in Austria［J］．European Journal of Forest Research，2011，130(4):521－531．

［12］符利勇，孙华．基于混合效应模型的杉木单木冠幅预测模型［J］．林业科学，2013，49(8):65－74．

［13］郭艳荣，吴保国，刘洋，等．立地质量评价研究进展［J］．世界林业研究，2012，25(5):47－52．

［14］孟宪宇．测树学［M］．3版．北京:中国林业出版社，2006:118．

［15］孟宪宇，张弘．闽北杉木人工林单木模型［J］．北京林业大学学报，1996，18(2):1－8．

［16］刘微，李凤日．落叶松人工林与距离无关的单木生长模型［J］．东北林业大学学报，2010，38(5):24－27．

［17］刘强，李凤日，董利虎．基于树冠竞争因子的落叶松人工林单木生长模型［J］．植物研究，2014，34(4):547－553．

［18］刘洋，亢新刚，郭艳荣，等．长白山主要树种直径生长的多元回归预测模型:以云杉为例［J］．东北林业大学学报，2012，40(2):1－4．

［19］Grote R．Estimation of crown radii and crown projection area from stem size and tree position［J］．Annals of Forest Science，2003，60(5):393－402．

［20］田晓筠．林木直径与冠幅的灰色模型及应用［J］．科技资讯，2008(25):86．

［21］韦雪花，王佳，冯仲科．北京市13个常见树种胸径估测研究［J］．北京林业大学学报，2013，35(5):56－63．