一种基于MFCC与PCP联合特征的和弦识别方法
2015-03-04秦媛媛
李 锵,秦媛媛
(天津大学电子信息工程学院,天津 300072)
一种基于MFCC与PCP联合特征的和弦识别方法
李 锵,秦媛媛
(天津大学电子信息工程学院,天津 300072)
结合乐理理论和信号处理理论,针对传统和弦识别仅考虑音高特性的音级轮廓特征PCP(pitch class profile)造成正确识别率较低的问题,提出一种以反映听觉特性的MFCC(mel frequency cepstral coefficent)与PCP的联合特征和稀疏表示分类器(sparse representation classification,SRC)的和弦识别方法.通过对两特征矢量的叠加构成新的和弦特征,然后利用SRC进行和弦识别.实验结果表明,与传统方法的识别率相比,本方法的识别率大幅提高.
和弦识别;MFCC;PCP;MFCC+PCP;稀疏表示分类器
音乐信号处理是近年来人工智能与模式识别领域的研究热点,和弦作为音乐信号重要的中层特征之一,是由3个或3个以上的不同音按照一定规则组合并同时发音形成的.不同和弦组成的和弦序列通过音符之间的和谐程度及高低差别表征不同的旋律,充分表达了一段音乐的内容和特征[1],对于实现音乐信息检索、乐曲分割与匹配以及歌曲自动翻唱具有重要作用.因此,和弦识别的研究具有很广泛的应用价值.音乐和弦识别主要包括和弦特征提取和识别模型的确定.比较有代表性的研究工作是Brown[2]首次将音乐识别与音乐理论结合,提出恒Q变换;Fujishima[3]在1999年率先提出12维音级轮廓(pitchclassprofile,PCP),将音乐信号能量映射到12个音级上,重建音级谱,最后利用模板匹配法识别和弦,取得了一定效果.Gomez[4]在此基础上提出HPCP(harmonic PCP)特征用于和弦识别的键估计系统中并取得了66.7%的正确键估计;Lee[5]使用谐波产物谱(harmonic product spectrum,HPS)提出一种增强型的PCP特征,与传统的PCP特征相比,增强型PCP对具有相同根音的和弦具有更高的识别率.Sheh和Ellis[6]提出将统计学方法即隐马尔可夫模型(hidden markov model,HMM)模型运用于和弦的分割与识别.Wang[7]结合人耳听觉特性和音乐理论提出了新的识别特征MPCP(Mel PCP),克服了PCP特征在低频段特征模糊和峰值处容易发生混倄的缺陷,但采用了条件随机场分割方法,运行时间长;文献[8]则采用卷积神经网络进行和弦识别,可以有效避免噪声对和弦识别率的影响,但该方法能识别的音频数量较小.稀疏表示[9]是最小一范数[10]的优化方法,在模式识别领域的相关研究中取得了很多可观的成果.本文将稀疏表示方法引入和弦识别模型学习与分类.传统的PCP特征没有考虑到人耳听觉特性,在低频段比较模糊,而MFCC[11]特征恰好能够弥补这一缺陷,充分描述了和弦旋律的低频段.本文将传统恒Q变换的PCP特征与梅尔倒谱系数(MFCC)相结合,提出一种基于MFCC与PCP的联合特征,并引入稀疏表示分类器,根据最小一范数实现对待测和弦的类型识别.
1 基于MFCC+PCP联合特征的和弦识别系统
本文和弦识别算法的特征提取部分包括:MFCC和PCP特征提取.和弦的具体识别过程如图1所示.

图1 基于MPCP特征的和弦识别流程图Fig.1 Flow chart of chord recognition based on MPCP
对训练样本和测试样本的每个和弦音频均提取MFCC和PCP 2种特征,然后对2种特征向量相加得到训练样本特征集和测试样本特征集的MFCC+PCP特征,再将2特征集矩阵输入到SRC分类器中,得到和弦识别结果.
1.1 和弦的特征提取
1.1.1 MFCC特征提取
Mel频率倒谱系数(MFCC)由Davis和Mermelstein[10]于1980年基于人耳听觉特性和语音生成原理提出,MFCC特征被广泛的应用到语音识别研究中.
对于音频信号而言,MFCC特征具体的计算步骤如下.
第1步:将时域离散和弦音乐信号进行预加重,分帧和加窗处理.预加重滤波器是一阶的,系统函数为H(z)=1-uz-1;取帧长为N,帧移为N/2;所加窗的窗函数类型为汉明窗(Hamming).
第2步:经过快速傅里叶变换(FFT)转化为频域信号,得到其频谱X(k).计算其能量谱

第3步:用M个Mel频率带通滤波器Hm(k)进行滤波;滤波器输出值为Pm(k),m=1,2,…,M.
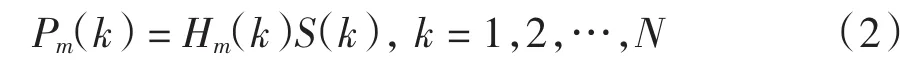
第4步:将每个滤波器的输出值Pm(k)取自然对数,得到Mm(k),m=1,2,…,M.
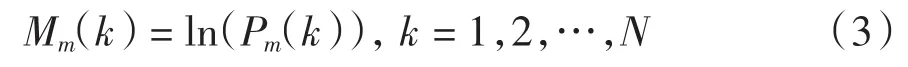
第5步:对第4步所得的结果作离散余弦变换(DCT),对于每一帧信号,得到M个MFCC系数.
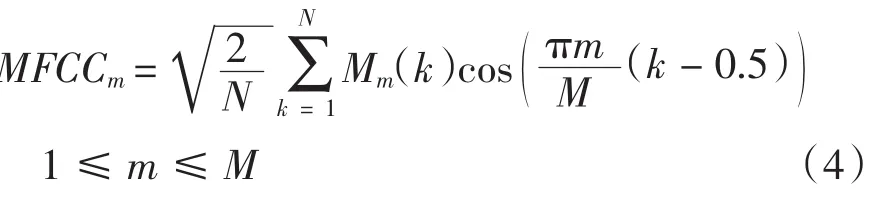
第6步:Mel滤波器的通道个数设置为M个,每个和弦样本得到的MFCC系数矩阵的大小为M*L,L为帧数.对每一帧第m(1≤m≤M)个滤波器的输出值MFCCm取平均值,公式为:

其中MFCCm(l)代表第l帧第m个滤波器的输出值.这样得到的每个和弦的MFCC统计平均值的大小为M×1.
1.1.2 PCP特征提取
音级轮廓(PCP)特征是由Fujishima[3]于1999年提出,将频谱重建为音级谱,然后将音乐信号能量映射到12个音级上.由于FFT和STFT估计音阶频率时的频率线是按线性分布的,所以两者频率点不能完全对应,致使某些音阶频率的估计值产生错误.因此在时频变换阶段采用了一种谱线频率与音阶频率具有相同指数分布规律的视频变换方法—CQT(Const-Q Transform,恒Q变换)[2].将经过CQT变换的PCP特征作为新的PCP特征,该特征包含丰富的音乐谐波结构.
PCP统计平均值特征的步骤如下.
第1步:时域离散和弦音乐信号x(m)分帧,加窗,进行恒Q(品质因数)变换(Constant Q Transform,CQT)将时域变换到频域.取帧长为N,帧移为N/2,所加窗的类型为汉明窗(hamming).
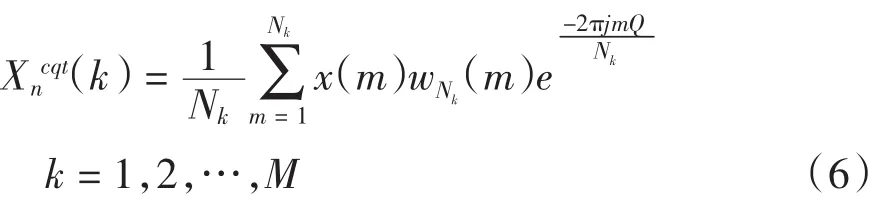
式(6)表示第n帧十二平均律中第k个半音的频谱,故通常M值为12.式中:x(m)为输入的时域离散和弦音乐信号;Nk=Qfs/fk表示第k个半音对应的窗长;fs表示采样频率;fk表示第k个半音的频率;wNk[m]表示窗长Nk为的hamming窗.
第2步:频谱映射.将频谱Xncqt(k)映射为音级域的p(k),它由12维向量组成,每维向量代表一个半音音级强度.按照乐理知识中的十二平均律以对数方式将频率映射到音级上,Xncqt(k)中的k被映射为PCP中的p,映射公式如下:

式中:f0=130.8 Hz为参考频率;fs为采样率;mod12为对12的求余运算.
第3步:通过累加所有与某一特定音级相对应的频率点的频率幅度平方值,得到每一帧信号的各个PCP分量的值.具体公式如下:
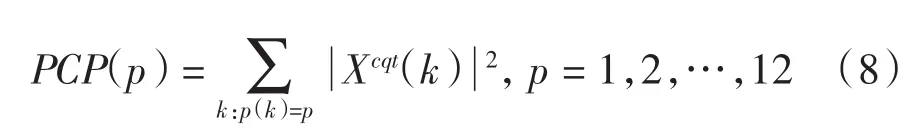
第4步:经过上面的计算得到一个12*L的矩阵音色图(chromagram),其中L代表帧数.计算每一个音级(行)的均值,公式如下:

经过上面的计算,得到一个12*1维的矢量,这就是所求的每个和弦样本的PCP统计平均值.
以大E和弦为例,其音色图和PCP图如图2所示.
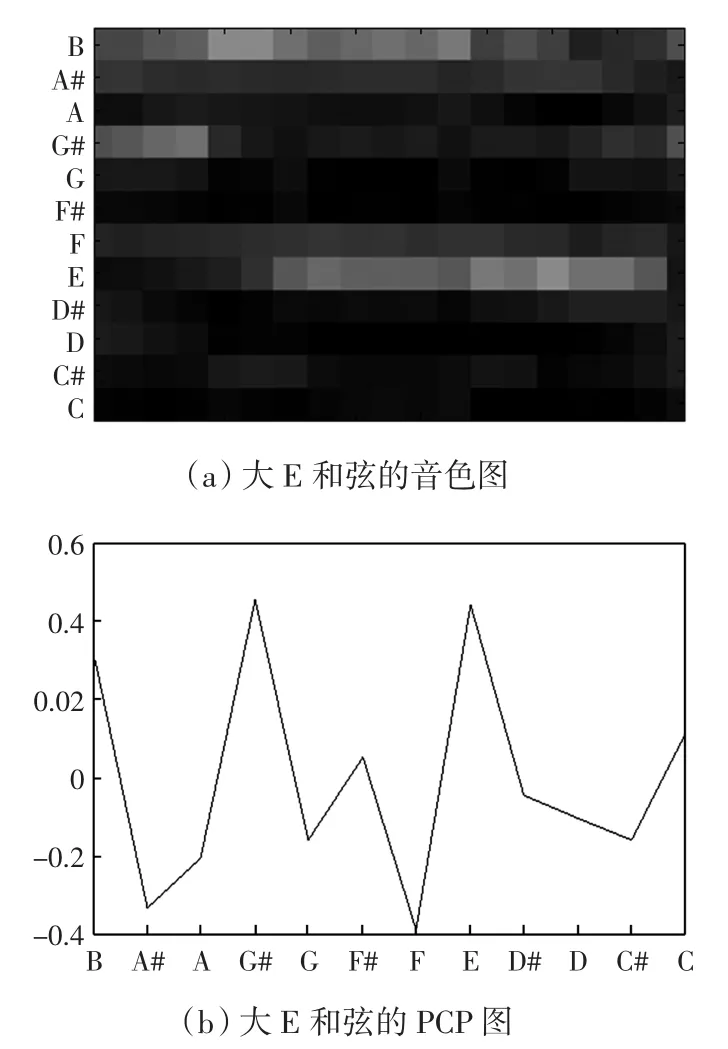
图2 大E和弦的音色图和PCP图Fig.2 Chromagram and PCP of E major
1.1.3 MPCP特征提取
MFCC作为和弦特征,虽然考虑了人耳听觉特性,但由于没有考虑到乐理知识、计算量和精度要求高,抑制了音高(pitch)信息,其识别效果并不好.
音级轮廓(PCP)作为和弦特征,虽然体现了音乐理论,但是没有充分考虑到人耳特性,在低频段特征比较模糊,在峰值附近容易发生混淆影响了识别效率.所以本文将M维MFCC统计平均值和12维PCP统计平均值连接,得到一个M+12维联合和弦特征值.和弦特征提取的具体流程如图3所示.
在物理实验的操作中,因为各方面的原因,出现数据偏差,实验现象与教材不符的几率非常的高,这些都是无法避免的。教师不应该“讳疾忌医”,而应该正视这些“意外”,在课堂上巧妙的应对实验误差和失败。当实验操作过程中,出现与课本不符的内容时,教师要改变既定方案,利用差错,生成更高价值的教学资源,培养学生的科学精神和科学态度。
1.2 基于稀疏表示的和弦识别
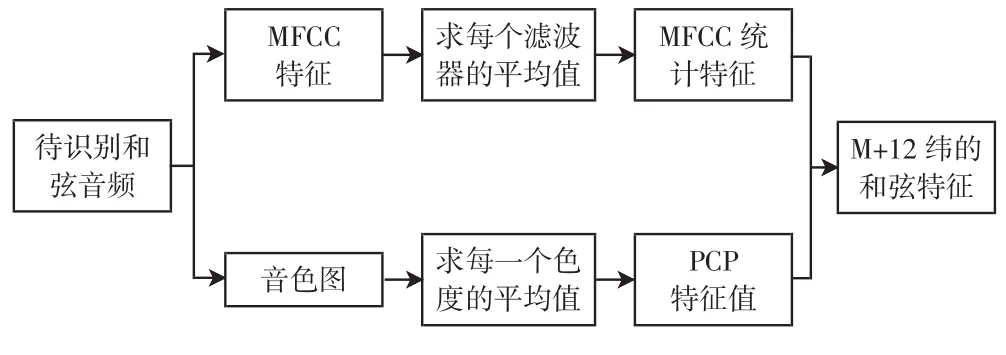
图3 提取和弦特征的流程图Fig.3 Flow chart of feature extraction
稀疏表示分类方法是在最小一范数基础上提出的,是模式识别领域热点研究课题,其分类思想是:在训练数据空间足够大的情况下,测试数据可以由训练数据空间中同类数据线性组合,找到最佳的稀疏向量.
在理想情况下,如果测试数据是训练数据中的某一类,则这个测试数据的线性组合就只能包含该类训练数据,即稀疏系数中只有一小部分是非零值.本文利用稀疏表示分类模型实现和弦识别.
1.2.1 稀疏表示模型
(1)稀疏表示方法.假设第i类训练样本的数据Ai=[vi,1,vi,2,…,vi,ni]∈Rm×ni,其中表示第i类样本数.完备训练样本数据矩阵A是由g类训练样本组成:

例如一个待测样本y属于训练样本的第k类,则由训练矩阵A构成的线性空间表示为

式中:x0=[0,…,0,ak,1,ak,2,…,ak,nk,0,…,0]T∈Rn为稀疏系数向量.在理想的情况下,除了该测试样本所属类别的系数不为零,其余的系数均为零.
(2)利用最小一范数求稀疏解.由压缩感知理论和稀疏表示[11]研究表明,若x0是稀疏的,则利用l1最小化范数求解式(11)可得

(3)基于稀疏表示的分类算法.通常情况下,由于存在噪声和建模误差,除k类以外,1在的其他类上的映射系数也会出现少量非零值.这时需要建立一个非零元素成分仅与和1第i类相关的新的向量来准确判断y的类别.所以,判断y的类别公式为

1.2.2 基于稀疏表示的和弦识别
本文提出的基于稀疏表示分类器的和弦识别算法分为如下5个步骤:①建立含有g类和弦的训练特征矩阵A=[A1,A2,…,Ag]∈Rm×n,其中Ai为第i类和弦的特征矩阵,m为特征个数,n为样本个数;②y∈Rm为待识别和弦样本的特征矢量,求出满足y=Ax,并使||x||1最小的解,其中=[1,2,…,K]T,i与Ai对应,i= 1,2,…,K;③分别保留K个和弦对应的系数i,构建K个矢量δi(1)=[0,…,0,i,0,…,0]T,i=1,2,…,K,矢量啄i(1)的维数与相同;④计算冗余值,即二范数为ri(y)=‖y-Aδi(1)‖2,i=1,2,…,k;⑤由最小冗余值对应的i确定y所对应的和弦.
以大E和弦为例,其最小一范数解和冗余值的求解过程,如图4所示.

图4 和弦类型识别的全过程Fig.4 Whole process of chord recognition
2 实验与分析
2.1 实验数据
本文选用的数据库是Beatles乐队的13部专辑的180首歌曲,Harte等[12]已经对这些歌曲中的和弦做了正确标注.实验中,输入的音乐文件格式是采样率为11 025 Hz,16 bit,单声道的wav格式.然后按所标注的和弦边界和类型从这180首歌中截取所需的大三和弦和小三和弦共24类,1 152个样本组成训练数据,288个样本组成测试数据,数据几乎涵盖了该乐队的所有演奏风格.
2.2 结果分析
本文实验先对所截取的训练数据和测试数据分别提取MFCC、PCP、MFCC+PCP联合特征,然后将特征分别输入到SRC识别模型中,并与经典的统计模型隐马尔可夫(hidden markov model,HMM)的识别方法作对比,实验结果表明,提取的MFCC+PCP特征与SRC模型结合效果最好,识别结果对比如表1所示.
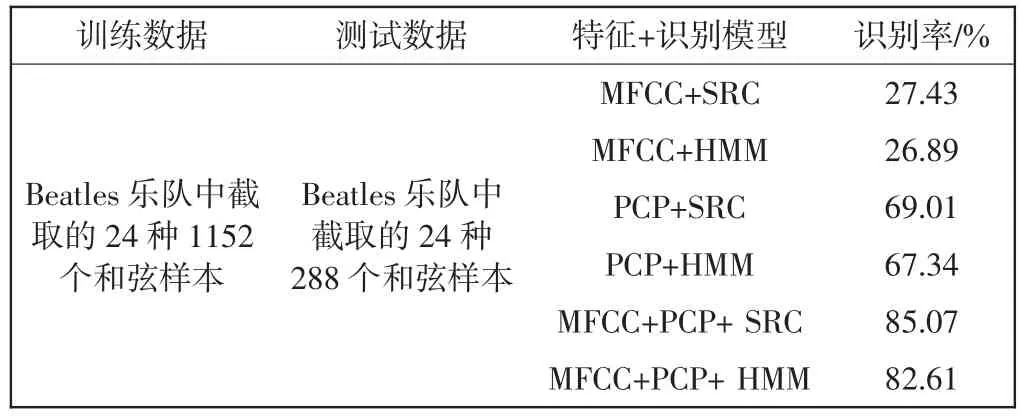
表1 识别结果对比Tab.1 Contrast result
通过对表1的和弦识别结果分析发现,MFCC+ SRC与MFCC+HMM组合模型识别率最低,由于MFCC没有考虑音乐乐理特征,抑制了音频的音高(Pitch)信息,导致和弦识别率低;PCP+SRC与PCP+ HMM识别模型虽然比MFCC+SRC与MFCC+HMM模型识别率高出40%左右,但识别率也只有69%和67%左右,因为PCP特征无法识别空和弦与具有相同根音和弦的情况,所以识别率不高;MFCC+PCP+SRC识别模型充分考虑了人耳听觉特性和音乐乐理特征,能够达到85.07%的识别效果,同时从表1中可以得出SRC模型要比HMM识别率高2%~3%左右,因为SRC可以有效地避免由于增加数据特征集而影响和弦识别率的问题.
3 结束语
本文提出一种基于MFCC与PCP联合特征和SRC分类器的和弦识别方法.实验结果表明,MFCC与PCP联合特征既符合人耳听觉特性,又符合和弦乐理上的特性,与传统基于MFCC和PCP单一特征和弦识别高出近20%和60%方法.同时,对于分类器的选择,SRC比HMM的识别率高出3%左右.下一步将研究如何融入更加丰富的乐理知识来进一步提高和弦识别率.
[1] 董丽梦,关欣,李锵.基于稀疏表示分类器的和弦识别研究[J].计算机工程与应用,2012,48(29):133-219.
[2]BROWN J.Calculation of a constant Q spectral transform[J].J Acoust Soc Amer,1991,89(1):425-434.
[3]FUJISHIMA T.Realtime chord recognition of musical sound:A system using common lisp music[C]//ICMC.1999:464-467.
[4]GOMEZ E,HERRERA P.Automatic extraction of tonal metadata from polyphonic audio recordings[R]//London:Audio Engineering Society,2004.
[5]LEE K.Automatic chord recognition from audio using enhancedpitchclassprofile[C]//ProcIntComputMusicConf(ICMC). New Orleans:LA,2006.
[6]SHEH A,ELLIS D.Chord segmentation and recognition using EM-trained hidden Markov models[C]//Proc Int Conf Music Inf Retrieval(ISMIR).Baltimore:MD,2003:185-191.
[7]WANG Feng,ZHANG Xueying,LI Bingnan.Research of Chord Recognition based on MPCP[C]//Proc The 2nd International Conference on Computer and Automation Engineering(ICCAE).IEEE Press,2010:76-79.
[8]HUMPHREY Eric J,BELLO Juan P.Rethinking Automatic Chord Recognition with Convolutional Neural Networks[C]// Proc The IEEE 11th International Conference on Machine Learning and Applications(ICMLA).Washington,DC,2012:357-362.
[9]DUAN GangLong,WEI Long,LI Ni.A multiple sparse representation classification approach based on weighted residuals [C]//The IEEE Ninth International Conference on Natural Computation(ICNC).2013:995-999.
[10]徐星.基于最小一范数的稀疏表示音乐流派与乐器分类算法研究[D].天津:天津大学,2011.
[11]王峰.美尔音级轮廓特征在音乐和弦识别算法中的应用研究[D].太原:太原理工大学,2010.
[12]DAVIS B,MERMELSTEIN P.Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences [C]//IEEE Transactionson Acoustics,Speech,and Signal Processing.1980:357-366.
[13]DONOHO D.For most large underdetermined systems of linear equations the minimal-norm solution is also the sparsest solution[J].Comm on Pure and Applied Math,2006,59(6):797-829.
[14]HARTE C,SANDLER M,ABDALLAH S,et al.Symbolic representation of musical chords:A proposed syntax for text annotations[C]//Proc Int Conf Music Inf Retrieval(ISMIR).2005: 66-71.
A chord recognition method based on joint feature of MFCC and PCP
LI Qiang,QIN Yuan-yuan
(School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China)
Combined with music and signal process theory,the paper proposes a new chord recognition approach which utilizes the MFCC (Mel Frequency Cepstral Coefficent)reflecting auditory perception properties jointly with the traditional PCP(Pitch Class Profile)as the combined feature and SRC(Sparse Representation classification)to improve the recognition rate.The experimental results show that the recognition rata of the new method is much better in average than that of the traditional methods.
chord recognition;MFCC;PCP;MFCC+PCP;sparse representation classification
TP391.4
A
1671-024X(2015)01-0050-05
2014-11-07
国家自然科学基金项目(61471263,61101225,60802049);天津大学自主创新基金(60302015)
李 锵(1974—),男,博士,教授,主要研究方向为音乐信号处理、模式识别、医学图像处理.E-mail:liqiang@tju.edu.cn
