地空导弹阵地避雷针设计模型

蒋 伟,余明友,王 光,余 娟

（空军预警学院，武汉 430019）

地空导弹阵地避雷针设计模型

蒋 伟,余明友,王 光,余 娟

（空军预警学院，武汉 430019）

研究了地空导弹阵地工程设计中普遍存在的避雷针对发射空间的干涉问题，建立了关于避雷针位置和高度设计的数学模型，并进行了仿真分析，然后对3种设计方案进行比较，最终确定了单支主动式避雷针的设计方案，该方案能有效解决地空导弹阵地的防直击雷工程设计难题，对提高阵地在雷暴气候条件下的全天候作战能力具有重要意义。

地空导弹阵地，发射空间，干涉，数学模型

0 引言

地空导弹武器系统是指从地面上发射，用来攻击各种空中飞行目标的导弹武器系统，它由目标搜索指示系统、跟踪制导系统、导弹系统、发射系统、指挥自动化系统和支援保障系统等组成［1］。长期以来，地空导弹武器系统因其阵地面积大、装备数量多、工作电压低、防雷难度大，以及全天候工作要求等原因使其经常遭受雷击，如果避雷针架设点和架设高度选取不合理，将可能造成导弹发射后撞击避雷针的问题。文献［2-5］已对避雷针的结构性能以及保护范围进行分析研究，美国、俄罗斯等发达国家都装备了大量先进的地空导弹武器装备，这些发达国家在传统的防雷技术、设备和器材的开发设计及制造方面处于世界领先水平，实行三维空间的综合系统防护措施［6］。本文将从固定式地空导弹武器系统的部署方式、导弹发射的空间区域、避雷针的数学模型以及仿真实例计算等方面进行分析研究。

1 发射空间的固有干涉问题

1.1 地空导弹阵地的部署方式

根据地空导弹部队阵地选择的基本要求,阵地选择最主要影响因素要考虑制导雷达和目标指示雷达阵地要求,具体可着重从7个方面进行评价:符合上级作战意图、雷达阵地条件、机动能力、通信状况、水源状况、电源状况、社会状况［7］。

本文以某型地空导弹系统为例且假设该型地空导弹武器系统按照环形方式部署，布局方式如图1所示，发射阵地为圆形，制导雷达天线中心位于圆心，多个导弹发射架均匀分布在圆周附近，车头朝外，车身中轴线与制导雷达天线中心对齐［8］。

图1 环形部署方式示意图

1.2 导弹发射空间范围的界定

根据互联网上的资料可知某型地空导弹的空间发射范围如图2所示。

则导弹的发射禁区为：

式（1）、式（2）中 α 为导弹的仰角发射范围，β为导弹的水平转角发射范围，m为导弹的最大发射仰角，n为导弹的最小发射仰角，θ为导弹发射架中心与制导雷达中心连线所形成的发射禁区，本文假设 n=20°、m=60°、θ=15°。

图2 导弹发射禁区示意图

因此，在架设避雷针时，必须把避雷针设计安装在导弹发射车的发射禁区内，且避雷针的高度不能影响导弹的发射，如图3所示。

考虑雷电流流经避雷针引下线和接地装置时产生的高电位对附近设施的干扰，以及避雷针的撤收架设场地大小等因数，避雷针架设点的选取，必须同时满足下列3个条件：

①防止避雷针接地泄流时高电位对附近设施的干扰。发射阵地中心到制导雷达之间的电缆及控制信号线沿图3中的直线AD铺设。根据建筑物防雷设计规范第4.2.1节规定：独立避雷针和架空接闪线或网的支柱及其接地装置与被保护建筑物及其有联系的管道、电缆等金属物之间的地上间隔距离，按以下表达式确定［9］：

式（3）中，S是空气中的间隔距离（m）；Ri是接地装置的冲击接地电阻（Ω）；hx是被保护建筑物或计算点的高度。取Ri=4Ω，hx=5.9m代入式（3）可得：S≥1.836m，考虑到GB50057要求不小于3m，本文S取为3m；

②由于地空导弹的火焰会影响阵地上的其他设备，因此，地空导弹的阵地半径必须大于限定值，本文假设阵地半径为15m；

③为减小避雷针撤收架设难度，架设点的选取要使得避雷针架设高度最低，即避雷针距离导弹发射中心距离最近。

图3 导弹水平发射区域示意图

1.3 避雷针的数学模型

为了满足①~③3个条件，在图3中作直线EF平行于AD，与圆弧的交点为E，且EF与AD相距3m；根据几何知识可求得AE=15m，∠GAE=15°-arcsin（1/5）=3.460 6°。因此，避雷针架设点的架设范围是离导弹发射中心距离为15m的圆弧EG上。

为了分析在圆弧EG上避雷针所需架设的高度以及对导弹发射的影响，在图3的基础上，按照阵地各兵器的部署情况绘出了相邻3部发射架与制导雷达天线平台中心相对位置，如图4所示。

图4 发射阵地避雷针与相邻发射架的示意图

在ΔABH中，AB为相邻两个发射车中心点的距离，设为α；H为避雷针的架设点，在导弹的水平发射禁区圆弧EG上分布，AH为避雷针离相应的发射车中心点的距离，设为 b；∠HAG=δ，∠BAG=ε；BH为发射阵地B的中心点离发射阵地A避雷针之间的距离，设为Li。

由几何知识可知：

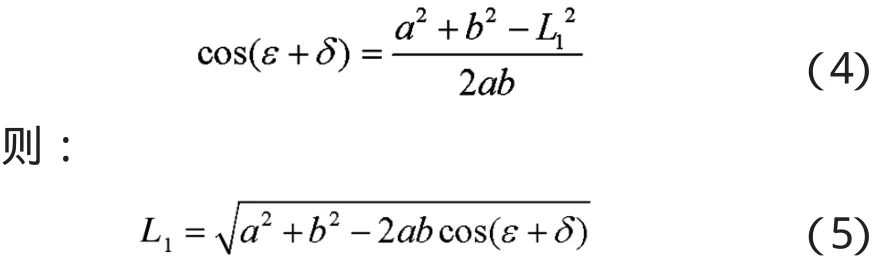
式（5）为避雷针架设点到相邻最近发射中心的距离。

图5 发射阵地B与点H避雷针示意图

在图5ΔOHH0中，为发射阵地B发射车中心点离发射阵地A避雷针之间的距离，为Li；H0H'为避雷针的高度，设为h，HH'为导弹发射点的高度，设为 h0；垂直发射角∠H0OH=μ。

由几何知识可知：

2 避雷针高度以及保护半径的计算

2.1 避雷针高度的仿真计算

当某型地空导弹武器系统按照环形方式部署时，假设相邻两个发射车A、B的距离a为50m；避雷针的位置取为图3中圆弧EG上（避雷针离发射车A中心点的距离b为15m）；导弹发射点离地面的高度h0为2m；发射阵地之间的夹角ε为30°；则不同垂直发射角μ以及不同夹角δ时，避雷针的临界高度仿真结果如图6所示。

从图6可以看出当导弹的仰角为20°，且避雷针在图3中圆弧EG上架设时（即夹角δ在0°到3.460 6°之间），避雷针的临界架设高度为16.85 m~17.12m之间，且为防止避雷针因导弹冲击波而发生变形损坏，避雷针在导弹飞行时，两者之间的距离不小于2m，即避雷针的临界架设高度为14.85 m~15.12m。且随着导弹仰角高度的增大或∠HAG增大时，避雷针的临界架设高度增大。

图6 避雷针的临界高度仿真图

2.2 避雷针保护半径的计算

当导弹围绕发射转轴作圆周运动，避雷针架设点、发射阵地中心点以及导弹中轴线在一条直线上时，兵器在其最高点的水平面内所需保护半径最大，如图7所示。

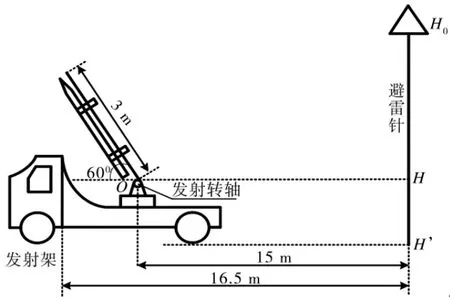
图7 发射车所需保护半径示意图

图7中L为架设避雷针到发射阵地A中心点的距离,假设导弹的长度为L1=3m，导弹所需的最大保护半径为R=L+L1cos60°。其中L=15m，可以推出R=16.5m。假设避雷针架设在图3中的G点，则由图6可知在G点架设避雷针时，其临界高度为16.85 m，考虑导弹飞行初期下降高度的影响，假设为2m，即避雷针的架设高度为14.85m。根据建筑物防雷设计规范第3.0.2节规定：凡制造、使用或贮存火炸药及其制品的危险建筑物，且电火花不易引起爆炸的应划为第2类防雷建筑物，则滚球半径hr=45m，在图7所示状态下导弹尖端的高度为4.55m，按照普通避雷针架设时保护半径的计算公式为［10］：

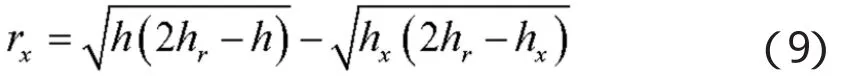
式中h为避雷针的架设高度；hr为滚球半径；hx为被保护物的高度。

如果在避雷针尖端架设主动式接闪器，根据NFC-17-102标准所提供的计算方法，保护半径按如下公式计算［11］：

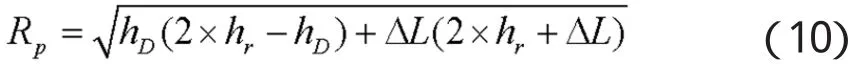
式中，hr为电击距离即滚球半径；hD为防雷器顶端到被保护平面的高度；ΔL为启动抢先距离，等于V×ΔT，通常情况 V=106m/s，ΔT=40ms~60μs，本文计算时假设ΔT=40μs。

表1根据式（9）、式10列出了导弹在不同垂直发射角时所需保护半径与普通避雷针、主动式避雷针的保护半径。

表1 所需保护半径与实际的保护半径

分析表1可知，在不同导弹发射角度下，普通避雷针的保护半径均小于其所需保护半径，而主动式避雷针的保护半径均大于其所需保护半径。

根据上述参数，设计3种方案：①单支传统避雷针保护一部兵器；②双支传统避雷针保护一部兵器；③一个主动式接闪器保护一部兵器。根据式(9)和式(10)，结合表1，运用SolidWorks软件仿真，仿真结果如图8所示。

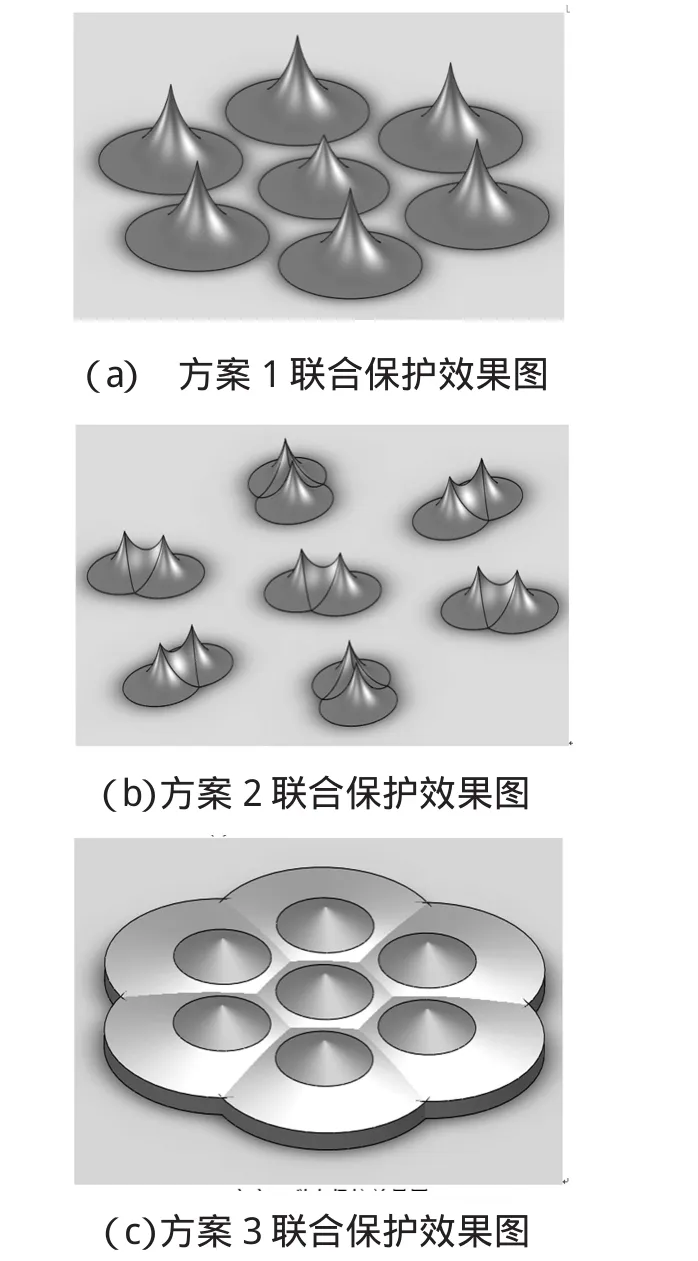
图8 3种方案的仿真图

利用方案1和方案2对发射阵地进行直击雷防护，虽然设计简单，但是避雷针数量多，施工难度大，成本高。大量的避雷针增大了雷达的遮蔽角，严重影响了雷达的探测范围，同时，避雷针产生的近距离反射波，会加快雷达接收机的老化速度。利用主动式接闪器虽然设计复杂，但是数量少，对雷达遮蔽角影响小，成本低。方案3不仅避雷针架设高度低，联合保护范围广，还能对阵地上的人员进行直击雷防护。

地空导弹阵地上的目标指示雷达天线也是防直击雷的重点，假设其高度为12m，宽15m。目标指示雷达天线需要保护的空间为天线转动时的圆柱体空间，高度为12m，地面半径为150m。该雷达说明中明确规定：雷达天线中心距离避雷针等强电设施不小于20m。因此，避雷针在高度为12m的保护范围半径至少为35m，也应采用主动式接闪器对其进行直击雷防护。

3 结论

本文针对某型地空导弹阵地部署有雷达及导弹发射架等特殊兵器，且相邻导弹发射阵地导弹发射时有可能撞击避雷针的问题，构建了避雷针的数学模型，并对其进行仿真分析研究。然后通过3个限制条件进行实例仿真计算，确定了避雷针的架设范围，最后根据相邻导弹阵地的布局以及导弹飞行的仰角和方向，确定了避雷针的临界架设高度，并对该避雷针的保护范围与在不同导弹发射角时的所需保护半径进行计算比较，结果表明主动式避雷针的保护范围满足要求，能有效解决地空导弹阵地的防直击雷工程设计难题，具有一定的推广价值。

［1］杨建军.地空导弹武器系统概论［M］.北京:国防工业出版社，2006：1-2.

［2］谢施君，何俊佳，陈维江.避雷针迎面先导发展物理过程仿真研究 ［J］.中 国 电 机 工 程 学 报，2012，32（10）：32-40.

［3］郑江，林苗.确定避雷针保护范围的新方法探讨［J］.广西电力，2004（2）：16-18.

［4］马宏达.各种避雷针的结构及其防雷性能［J］.电网技术，2000，24（12）：16-18.

［5］戴祥军，贾英江，安振涛.危险球心法求解避雷针保护范围［J］.军械工程学院学报，2003，15（2）：63-66.

［6］肖稳安，李霞，陈红兵.防雷专业技术知识问答［M］.北京：气象出版社，2010.

［7］雷蕾，辛永平，龙正国.基于FAHP和改进模糊综合评判的地空导弹阵地优选［J］.火力与指挥控制,2012，37（9）：150-153.

［8］张梦.某型地空导弹阵地防雷系统研究与设计［D］.武汉:空军预警学院，2012.

［9］中华人民共和国住房和城乡建设部.建筑物防雷设计规范.GB 50057-2010.［S］.北京：中国建设出版社，2011.

［10］苏邦礼，崔秉球，吴望平，等.雷电与避雷工程［M］.广州：中山大学出版社，1996：45-56.

［11］孙旭光，魏晴昀，余明友.大型多雷达阵地直击雷防护方案研究［J］.空军雷达学院学报，2008，22（4）：239-242.

Research of Design M odelof Lightning Rod in Surface-to-air M issile Launcher Position

JIANGWei，YUMing-you，WANGGuang，YU Juan
（Air Force Early Warning Academy,Wuhan 430019，China）

This paper studies the common problem of interference between lightning rod and launch space in the engineering design of the surface-to-airmissile launcher position,establishes the mathematical model about the position and height of lightning rod,then carries out the simulation analysis and compares the three kinds of design scheme,lastly adopts the design scheme of signal active lightning rod.The design scheme effectively solves the problem of protecting the surface-to-airmissile position from the direct stroke lightning in the engineering design,and it is of great significance to improve the all-weather combat capability in the thunderstorm conditions.

surface-to-airmissile position，launch space，interference，themathematicalmodel

TJ630

A

1002-0640（2015）11-0127-04

2014-09-15

2014-10-27

蒋 伟（1989- ），男，浙江建德人，硕士研究生。研究方向：电磁环境分析与防护。