IEFG针对环形域内的Poisson方程的精确度研究
2015-03-03凌建国王丽萍
凌建国,王丽萍
(1.晋中师范高等专科校 晋中 030619; 2.太原科技大学 数学系 030027)
IEFG针对环形域内的Poisson方程的精确度研究
凌建国1,王丽萍2
(1.晋中师范高等专科校 晋中 030619; 2.太原科技大学 数学系 030027)
基于移动最小二乘插值法的基础上,对提出的插值型无单元Galerkin方法(IEFG)在环形域内的势问题的精确度的研究.IEFG方法运用于工程计算时,可以直接施加边界条件,通过对误差进行分析表明,IEFG方法在运用于工程计算时,确实也提高了计算精度.
无网格方法;移动最小二乘法;插值型无单元Galerkin方法(IEFG);权函数;形函数
势问题是科学和工程科学的重要内容之一.本文是针对势问题的Poisson方程展开的研究.本章中,IEFG方法是在传统的无单元Galerkin(EFG)方法基础上,对基函数进行了单位正交化,与EFG相比,该方法中,形函数具有插值特性,且边界条件可以直接施加,计算形式更加简便,计算精度更高等优点.通过对环形域内的Poisson方程的精确度研究,表明IEFG较EFG有更高的计算精度.
1 移动最小二乘法
定义区域Ω上的函数u(x),已知其在域内N个节点x1,x2,…,xN的函数值,取函数
(1)
为函数u(x)的逼近函数.这里pi(x)是基函数,ai(x)是相应的系数.定义如下泛函,它表示点x的紧支域内各点处误差的加权平方和:
(2)
其中ω(x-xI)是具有紧支集特性的权函数,xI(I=1,2,…,n)为点x的紧支域内的节点.
系数ai(x)(i=1,2,…,m)的选择总是使泛函取极小值,
(3)
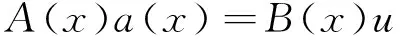
(4)
其中矩阵A(x)和B(x)分别为
(5)
(6)
可得
(7)
这样,逼近函数uh(x)的表达式为
(8)
其中Φ(x)为形函数
(9)
这样,当u(x)为二元函数时, 逼近函数uh(x)的表达式为
(10)
(11)
2 移动最小二乘插值法

把基函数p1(x)≡1在x点单位化为
(12)

(13)
(14)
这时可以证明
(15)
所以逼近函数经过插值节点.
3 势问题的插值型无单元Galerkin方法(IEFG)
考虑二维poisson方程
(16)
(17)
(18)
其中Ω是问题的所在区域,Γ为Ω的边界,且有
Γ=Γu∪Γq,Γu∩Γq=Φ;
(19)
式(16)、(17)、(18)的等效积分弱形式为
(20)
将式(10)代入式(20),得
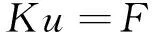
(21)
其中,
(22)
(23)
(24)
(25)
(26)
(27)
(28)
环形域上的泊松方程的狄利克雷问题
(29)
狄利克雷边界条件:

(30)
这个问题的解析解为
(31)
如图1所示,在环形域内沿着半径方向布置了101*11个节点,图2和图3分别给出了不同布点下,环形域内的解析解和数值解.随着节点数的增加,数值解与解析解也越接近.通过图4可知,权函数半径固定时,随着节点数的增加,相对误差范数也越小.
为进一步验证理论证明的有效性,图5给出了权函数影响域半径与相对误差范数之间的关系,即节点分布固定时,权函数半径r越小,相对误差范数也越小,计算结果越精确.但注意,r充分小,也应保证影响域的并集覆盖整个区域,否则也会影响数值解的精确度.

图1 节点分布
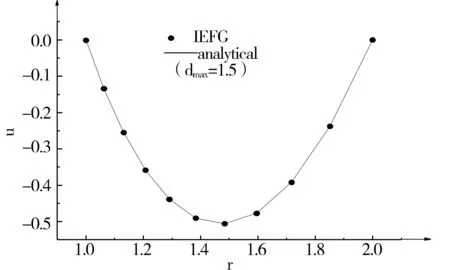
图2 解析解和数值解的对比
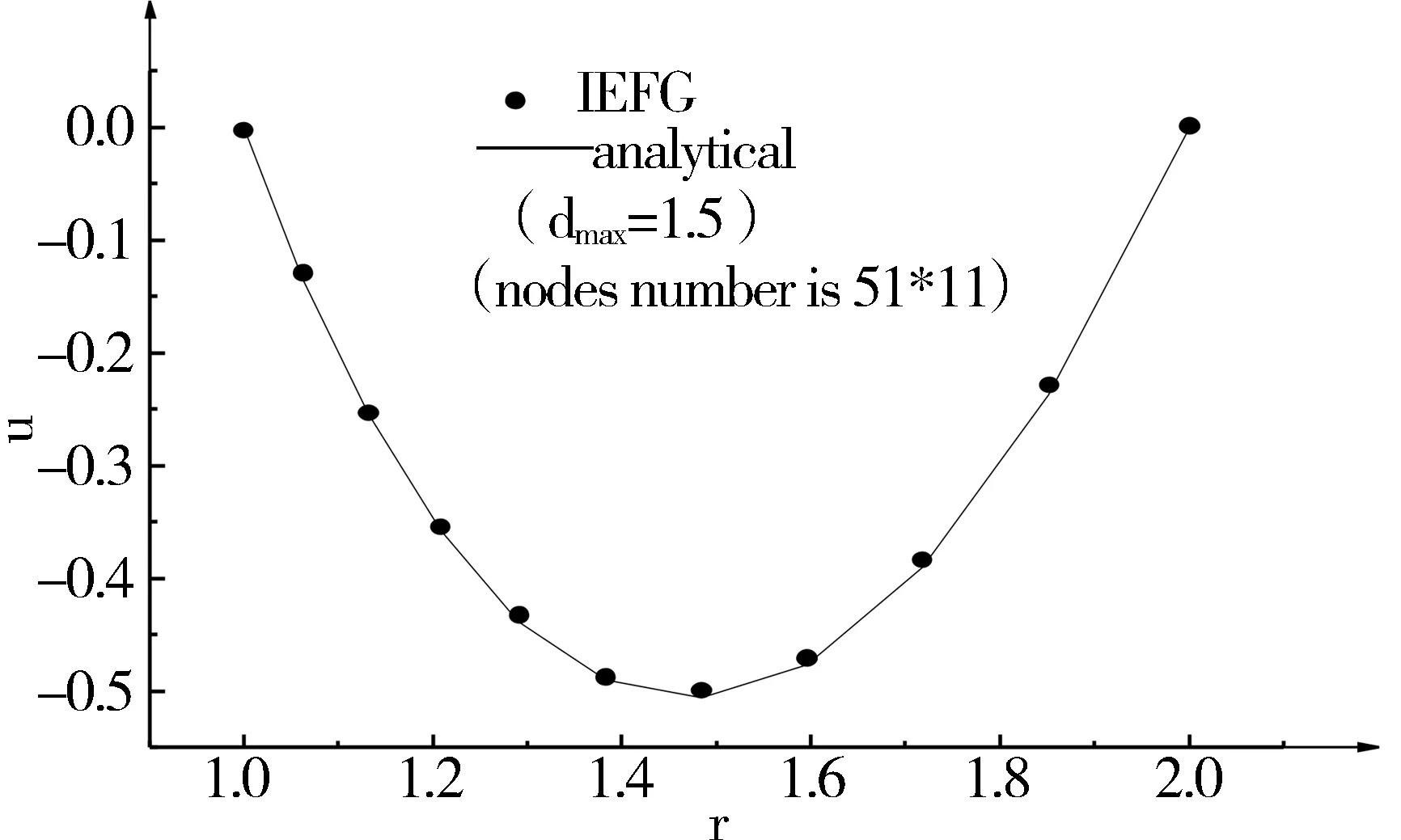
图3 解析解和数值解的对比(51*11个节点)

图4 相对误差范数和影响半径之间的关系
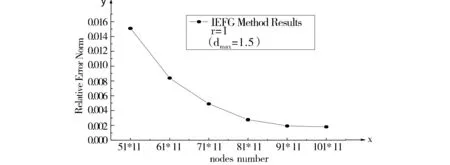
图5 相对误差范数和节点分布之间的关系
4 结论
针对Poisson方程的误差分析表明,该误差与权函数的影响域半径和节点分布密切相关.数值解与解析解的误差范数的上界与权函数的影响域半径密切相关,权函数的影响半径的值越小,误差值就越小,数值越精确.但注意,r充分小,也应保证影响域的并集覆盖整个区域,否则也会影响数值解的精确度.通过数值算例表明,IEFG在提高计算精度方面比传统的无单元Galerkin(EFG)方法更有效.
[1] Belytschko T,Krongauz Y,Organ D.Meshless method:An overview and recent developments[J].Computer Methods in Applied Mechanics and Engineering,1996,139:3-47
[2] LANCASTER P,SALKAUSKAS K.Surfaces generated by moving least square methods[J].Mathematics of Computation,1981,37:141-158
[3] Belytschko T,Lu Y Y,Gu L.Element-free Galerkin Methods[J].International Journal for Numerical Methods in Engineering,1994,37:229-256
[4] Mukherjee Y X,Mukherjee S.On boundary conditions in the element-free Galerkin method[J].Computational Mechanics,1997,19:264-270
[5] 任红萍,改进的移动最小二乘插值法研究[J].工程数学学报,2010,12(6):1021-1029
[6] Ren H,Cheng Y.The interpolating element-free Galerkin(IEFG)method for two-dimensional potential problems.Engineering Analysis with Boundary elements,2012,36(5):873-880
IEFG Study the Accuracy of the Circular Poisson Equation in the Domain
Ling Jianguo1, Wang Liping2
(1.Jinzhong Teachers’College, Jinzhong 030619;2.Taiyuan University of Science and Technology, Taiyuan 030027, China)
To study that method (IEFG)’s the domain of the potential problems in the ring the accuracy ,which is based on moving least square interpolation method,IEFG method applied to engineering calculation, and it can be directly applied boundary conditions.IEFG method applied to engineering calculation, does improve the calculation accuracy ,through the error analysis.
meshless method; the moving least squares method; interpolation type Galerkin method(IEFG); no unit weight function; the form of a function
2015-01-26
凌建国(1974-),男,山西晋中人,硕士,晋中师范高等专科学校讲师,主要从事偏微分方程及工程数值计算研究.
1672-2027(2015)02-0017-04
O242
A
