IEFG针对矩形域内的Poisson方程的精确度研究

王丽萍,任红萍

(太原科技大学 应用科学学院,山西 太原 030024)

IEFG针对矩形域内的Poisson方程的精确度研究

王丽萍,任红萍

(太原科技大学 应用科学学院,山西 太原 030024)

在移动最小二乘插值法的基础上,对插值型无单元Galerkin方法(IEFG)在矩形域内的势问题的精确度进行研究．IEFG方法在运用于工程计算时,可以直接施加边界条件,具有计算简便精度高的优点．

无网格方法;移动最小二乘插值法;插值型无单元Galerkin方法(IEFG);权函数;形函数

1 预备知识

IEFG作为无网格方法的一种新的数值方法,它满足Kronecker Delta函数的性质,具有插值特性,相对于传统的无单元Galerkin(EFG)方法,它克服了需要利用Lagrange乘子法等方法来施加边界条件,对边界条件可以直接施加,计算不仅简便,而且计算精度高．本文是把矩形域内的Poisson方程作为研究对象,针对IEFG的计算精度进行的研究[1-4]．

2 移动最小二乘逼近法

定义区域Ω上的函数u(x),已知其在域内N个节点x1,x2,…,xN的函数值,取函数

(1)

为函数u(x)的逼近函数．这里pi(x)是基函数,ai(x)是相应的系数．定义如下泛函,

(2)

其中ω(x-xI)是具有紧支集特性的权函数,xI(I=1,2,…,n)为点x的紧支域内的节点．

对J求极值,求出系数ai(x)(i=1,2,…,m)

(3)

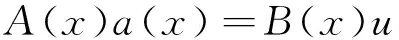
(4)

其中矩阵A(x)和B(x)分别为

(5)

(6)

可得

a(x)=A-1(x)B(x)u

(7)

这样,逼近函数uh(x)的表达式为

(8)

其中Φ(x)为形函数

(9)

这样,当u(x)为二元函数时, 逼近函数uh(x)的表达式为

(10)

(11)

3 插值型移动最小二乘法

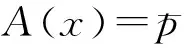
把基函数p1(x)≡1在x点单位化为

(12)

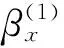
(13)

(14)

这时可以证明

(15)

所以逼近函数经过插值节点.

4 势问题的插值型无单元Galerkin方法(IEFG)

考虑二维poisson方程

(16)

(17)

(18)

其中Ω是问题的所在区域,Γ为Ω的边界,且有

(19)

式(16)、(17)、(18)的等效积分弱形式为

(20)

将式(10)代入式(20),得

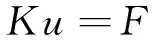
(21)

其中,K=∫ΩBT(x)·B(x)dΩ

(22)

(23)

F(1)=(F(1)(x1),F(1)(x2),…,F(1)(xnt))T

(24)

F(1)(xI)=∫ΩΦIbdΩ

(25)

F(2)=(F(2)(x1),F(2)(x2),…,F(2)(xnt))T

(26)

(27)

F=F(1)+F(2)

(28)

5 数值算例

矩形域上泊松方程的狄利克雷问题

(29)

T(x,y)=0在矩形域的边界上,

(30)

这个问题的解析解是

T(x,y)=(x-x2)(y-y2)

(31)

图1表示矩形域内的11*11的节点分布，图2、图3分别表示温度在x=0.5,y=0.6时的数值解，图4表示相对误差范数和影响半径之间的关系，图5表示相对误差范数和影响半径之间的关系。

图1 节点分布

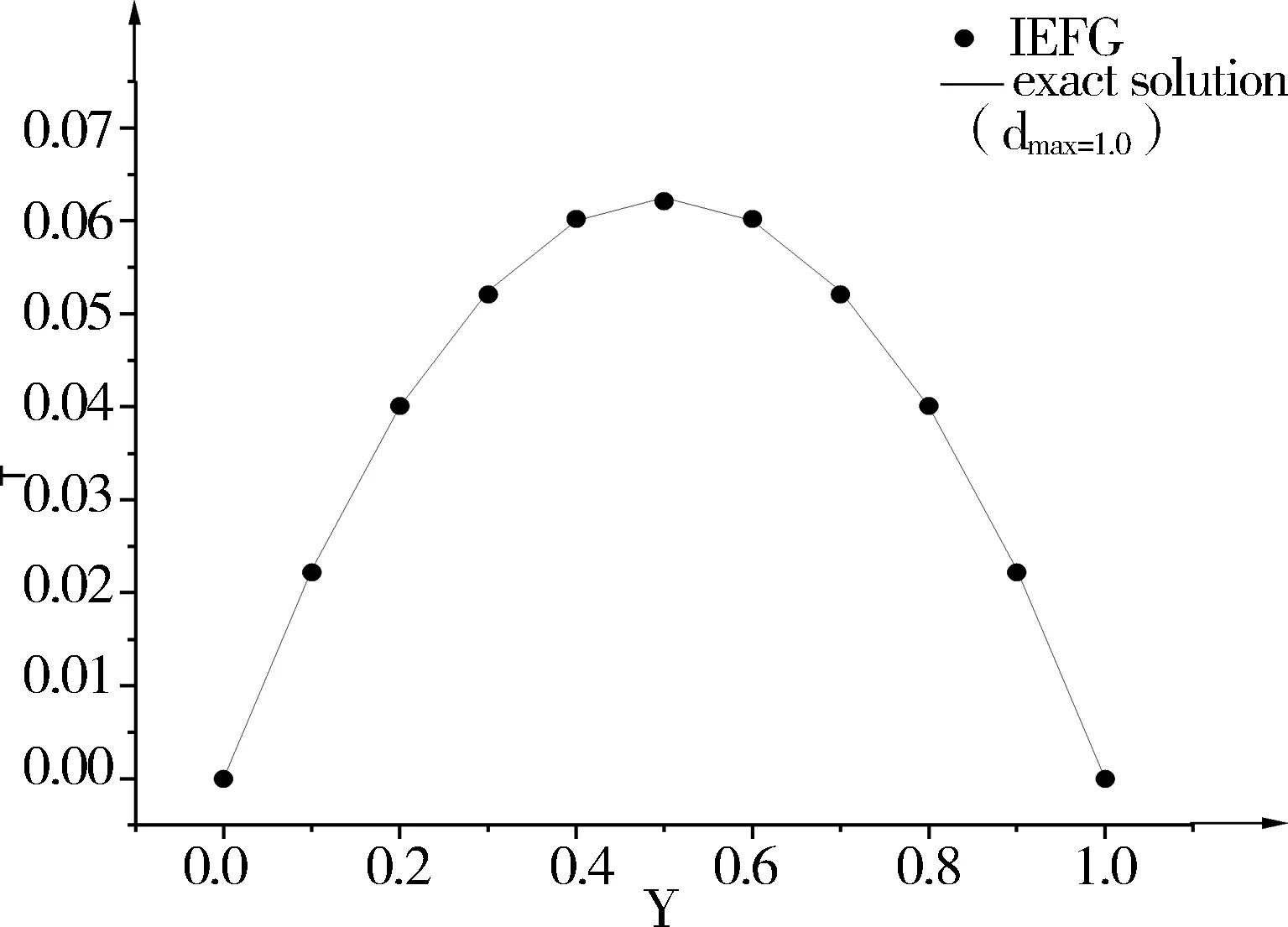
图2 x=0.5处温度的解析解与数值解

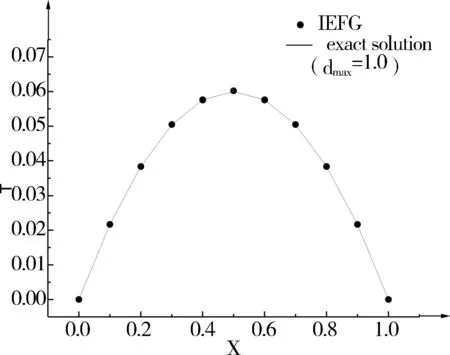
图3 y=0.6处温度的解析解与数值解

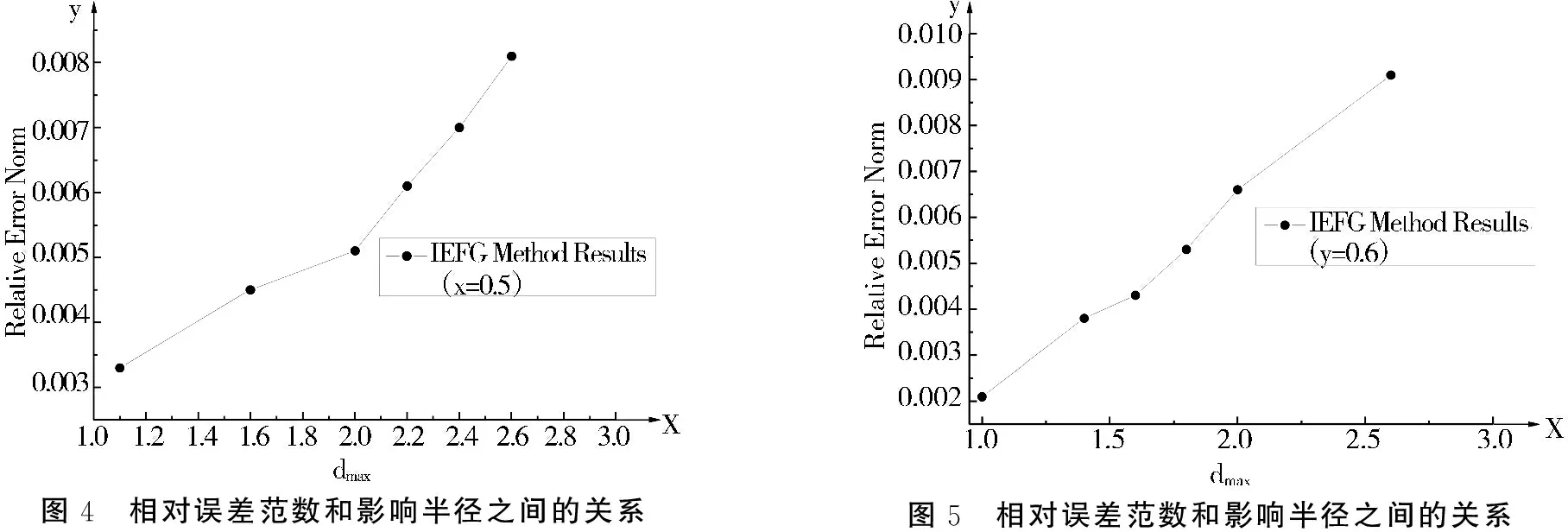
图4 相对误差范数和影响半径之间的关系图5 相对误差范数和影响半径之间的关系

6 结论

针对矩形域上的Poisson方程的误差分析表明,数值解与解析解的相对误差范数与权函数的影响半径密切相关,权函数的影响半径的值越小,误差值就越小,数值越精确,但是影响半径充分小,就会导致系数矩阵的奇异,所以权函数影响半径的选取要小,但要保证影响域的并集要覆盖整个区域,通过数值算例表明,IEFG在提高计算精度方面比传统的无单元Galerkin(EFG)方法有更高的计算精度．

[1] Belytschko T,Krongauz Y,Organ D.Meshless method:An overview and recent developments[J].Computer Methods in Applied Mechanics and Engineering,1996,139:3-47

[2] Lancaster P,Salkauskas K.Surfaces generated by moving least square methods[J].Mathematics of Computation,1981,37:141-158

[3] Belytschko T,Lu Y Y,Gu L.Element-free Galerkin Methods[M].International Journal for Numerical Methods in Engineering,1994,37:229-256

[4] Mukherjee Y X,Mukherjee S.On boundary conditions in the element-free Galerkin method[J].Computational Mechanics,1997,19:264-270

[5] 任红萍.改进的移动最小二乘插值法研究[J].工程数学学报, 2010, 12(6): 1021-1029

[6] Ren Hongping, Cheng Jie, Huang Aixiang.The complex variable interpolating moving least-squares methed[J].Applied Mathematics and Computation,2012,219(4):1724-1736

IEFG Method Studies about the Accuracy of Poisson Equations in the Rectangular Domain

Wang Liping, Ren Hongping

(School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China)

To base on the interpolating moving least-squares method (IMLS), the study has proposed the interpolating element-free Galerkin(IEFG) method for the two-dimensional potential problems in a rectangular region. The IEFG method, which is applied in engineering calculation, the boundary conditions can be applied directly, and the error analysis shows that the IEFG method has higher calculation precision.

meshless method;interpolating moving least-squares method(IMLS); interpolating element-free Galerkin(IEFG) method; weight function; shape function

2014-10-29

山西省自然科学基金项目(2014011006-2);太原科技大学博士研究基金项目(20102024);太原科技大学研究生科技创新项目(20145010).

王丽萍(1984-),女,山西晋中人,太原科技大学应用科学院在读硕士研究生,主要从事偏微分方程及工程数值计算研究．

1672-2027(2015)01-0001-04

O242

A