基于分数阶PID的环形单级倒立摆稳定控制研究
2015-03-03廖伍代刘正博温盛军张翔铭
廖伍代, 刘正博, 温盛军, 张翔铭
(中原工学院, 郑州 450007)
基于分数阶PID的环形单级倒立摆稳定控制研究
廖伍代, 刘正博, 温盛军, 张翔铭
(中原工学院, 郑州 450007)
针对环形单级倒立摆的稳定控制,设计了基于分数阶的PID优化控制器。用拉格朗日方法建立的环形单级倒立摆系统模型是一个具有3个自由度的欠驱动系统,其整数阶PID控制器难以获得满意的控制性能。因此,提出基于分数阶PID的稳定控制,其分数阶PID参数采用Signal Constraint优化模块进行优化。对整数阶和分数阶PID控制效果进行分析比较,结果表明:相对于整数阶的PID控制,分数阶PID控制系统的倒立摆起摆迅速,稳定控制性能优良。
环形倒立摆;Signal Constraint优化模块;分数阶PID控制
倒立摆系统是一个多变量、高阶次、强耦合、非线性的自然不稳定系统,是检验各种控制理论的理想模型,一直是控制理论界关注的焦点[1-2]。目前,国内外关于倒立摆的研究大都集中在直线型倒立摆系统,而对环形倒立摆的研究较少。相对于传统型直线倒立摆,环形倒立摆具有3个自由度,克服了行程限制,是校验各种控制理论更理想的控制体系[3-4]。对于倒立摆系统,传统的PID控制很难达到理想的控制效果。因此,本文引入分数阶PID控制。分数阶PID控制器是传统整数阶PID控制器的拓展,它比整数阶PID控制器多了2个可调参数,即积分阶次λ和微分阶次μ,控制器参数整定范围变大,能够更灵活地控制受控对象[5]。为了解决人工大量试凑、精度不高等问题[6-7],本文提出利用Signal Constraint优化模块满足约束条件来获得控制器的最优参数,以期得到更好的控制效果。
1 环形单级倒立摆系统的数学模型
环形单级倒立摆由1个连杆、1个摆杆和1个质量块组成,其坐标系如图1所示。图中:l1为连杆的长度;l2为摆杆转动中心到杆质心的距离;θ1为连杆与y轴的夹角;θ2为摆杆与垂直向上方向的夹角(顺时针为正)。环形单级倒立摆的物理参数如表1所示。
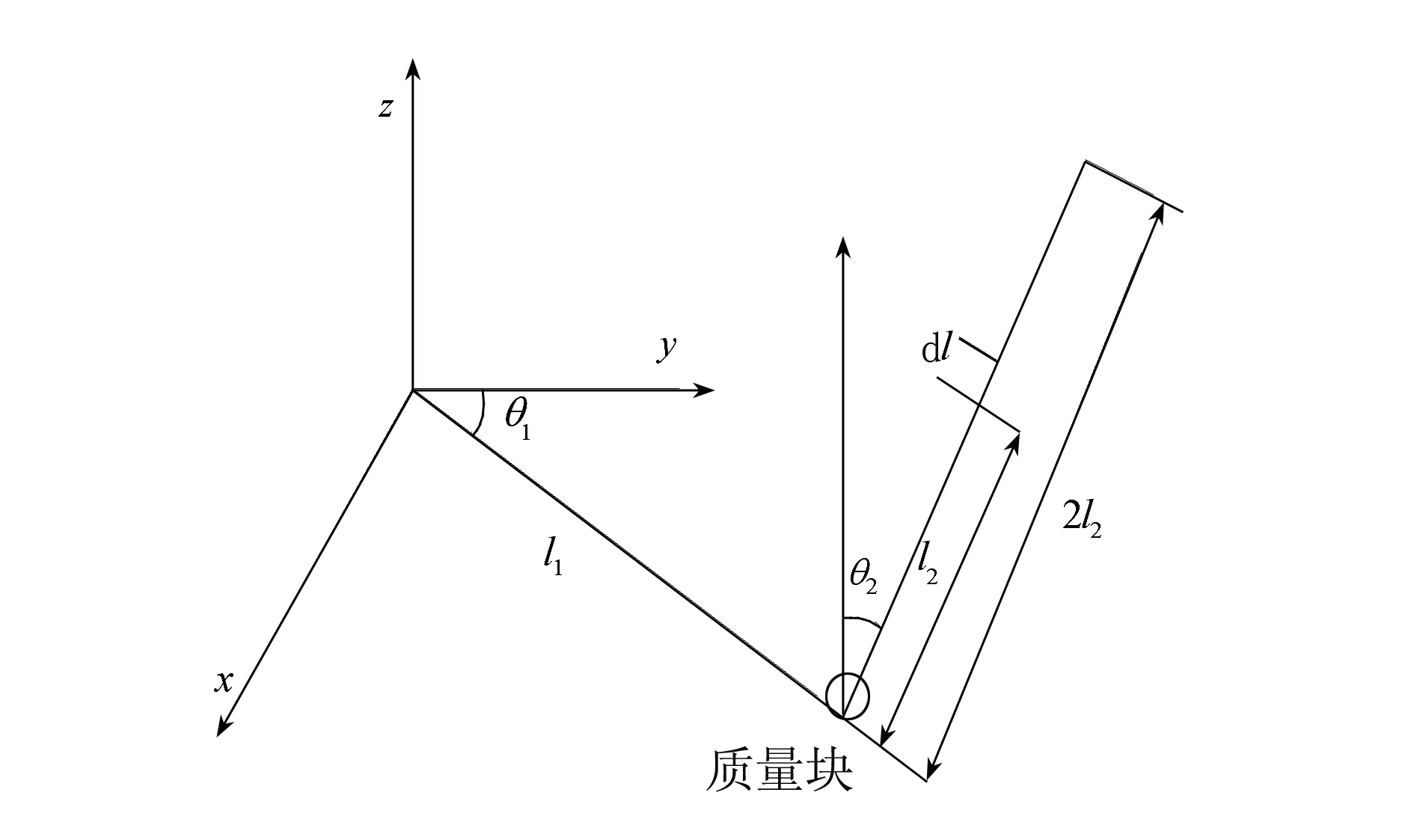
图1 环形单级倒立摆的坐标系

参数含义参数值m1/kg连杆的质量0.2340m2/kg摆杆的质量0.1323m3/kg质量块的质量0.1780l1/m连杆的长度0.2210l2/m摆杆质心到转轴的距离0.1975g/(m·s-2)重力加速度9.8
倒立摆运动方程的建立和分析方法主要有牛顿·欧拉方法和拉格朗日方法。这里利用拉格朗日方程推导得到环形倒立摆系统的运动方程。在摆杆上取一小段dl,dl的空间坐标设为(x,y,z):
(1)
则这一小段摆杆dl的动能dT为:
(2)

(3)
连杆的动能Tm1为:
(4)
质量块的动能Tm3为:
(5)
系统的总动能T为:
(6)
以连杆水平位置为0势能位置,则系统的势能等于摆杆的势能:
V=Vm1+Vm2+Vm3=0+m2gl2cosθ2+0=m2gl2cosθ2
(7)

由上述拉格朗日算法可以得到:
(8)
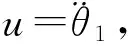
(9)
式中:Y(s)为系统输出的拉普拉斯变换;U(s)为系统输入的拉普拉斯变换;s为拉普拉斯算子。
2 环形倒立摆的稳定控制
2.1 基于Signal Constraint模块的PID优化控制
基于SignalConstraint模块的PID优化控制结构如图2所示。在SignalConstraint模块的优化过程中,简单搜索、梯度下降、遗传算法等优化方法为控制器参数优化提供了快捷方便的优化手段,尤其对于大型系统或者仿真速度较慢的系统,可以采用仿真技术加快优化速度。具体的优化步骤如下:①读取初始数据,并给予初始值;②计算目标和约束函数;③如果满足约束条件,优化结束,否则继续;④计算二次规划的目标函数;⑤线性搜索并更新Hessian矩阵,如果满足优化结果,结束命令,否则返回到③。
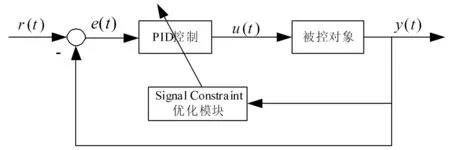
图2 Signal Constraint优化模块作用图
基于SignalConstraint优化模块建立环形单级倒立摆的Simulink仿真结构如图3所示。

图3 环形倒立摆PID控制仿真结构
双击SignalConstraint,打开Goals菜单,并从中选择DesiredResponse选项。这里可设置一些约束条件:上升时间为1s,调整时间为2s,超调为5%等(见图4)。然后,在Optimization菜单中选择TunedParameters,并将待调整参数加入。待调整参数需要在Matlab的CommandWindow中给出(见图5)。
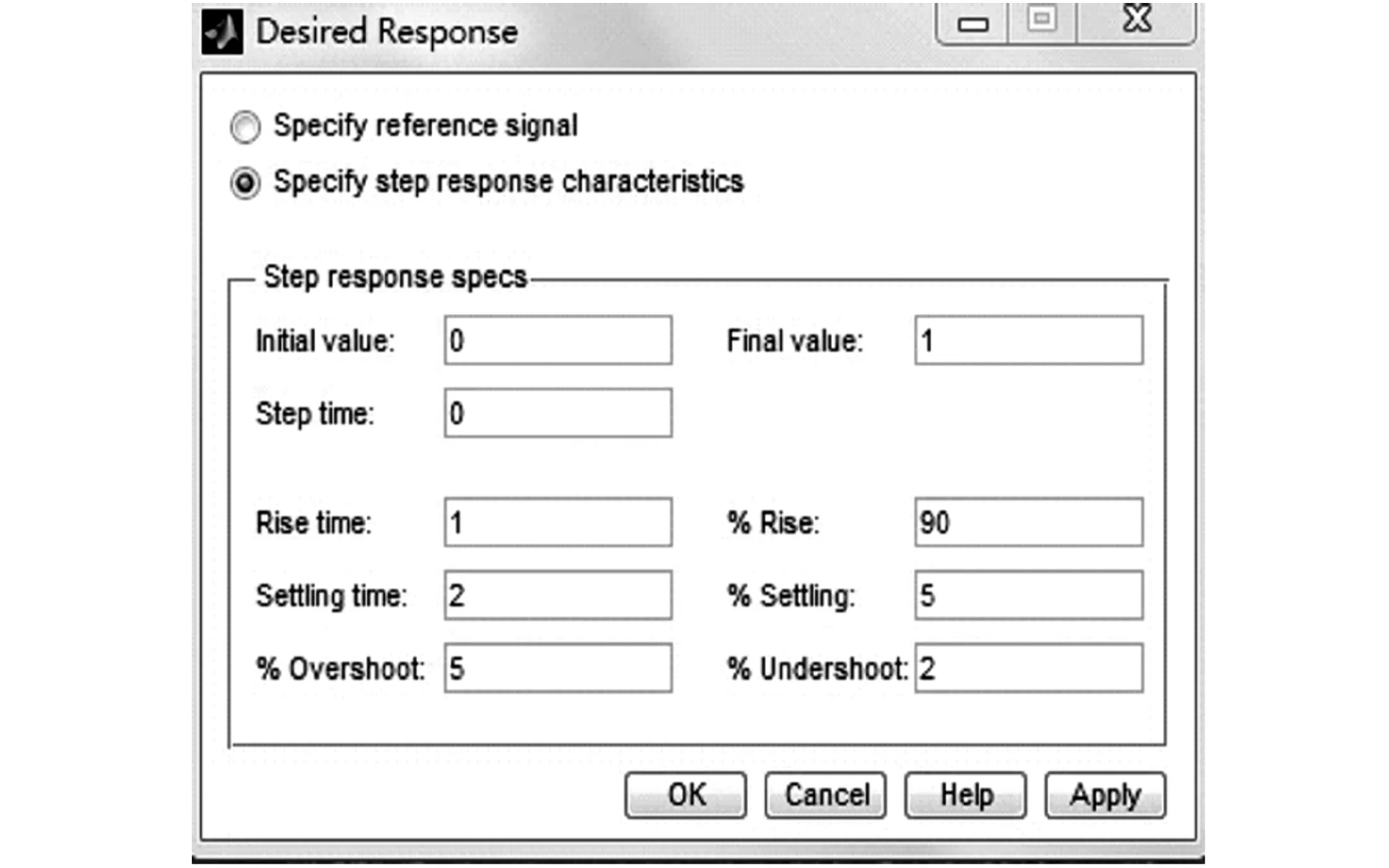
图4 Desired Response选项

图5 Tuned Parameters选项
完成目标建模和SignalConstraint模块的设置后,在SignalConstraint模块的主界面上点击StartOptimization选项,系统即可开始优化仿真。当系统优化完成后,SignalConstraint模块的主界面将会用黑线绘制出优化后参数的仿真曲线;同时,优化结果将生成一个报告。优化结果报告中包括重复次数、迭代
次数、网格大小、约束函数值及其方法,最重要的是给出了优化结论和待调整参数经过优化后的数值(见图6)。

图6 优化结果报告
2.2 分数阶PID优化控制器设计
由于分数阶PID控制器引入了微分阶次μ、积分阶次λ,因此,控制器参数的整定范围变大,控制器能够更灵活地控制受控对象,可以得到更好的控制效果。分数阶控制的意义就在于古典整数解控制的扩展化,它可以提供更多的模型,得到鲁棒性更好的控制效果[8]。
分数阶PID控制器的一般形式为PIλDμ控制器,包括一个积分阶次λ和一个微分阶次 μ,其中λ和μ可以是任意实数。其传递函数为:
(10)
分数阶PID控制器的参数优化同样可利用SignalConstraint模块对非线性控制系统进行优化设计和仿真,并在Simulink中建立如图7所示的非线性控制系统(闭环形式)的仿真模型。模型中阶跃信号模块、饱和特性模块的参数设置与PID控制器参数优化中的设置基本一致。因为在Simulink中没有分数阶PID控制器模块,所以本文编写了分数阶PID的Matlab工具箱,用来完成仿真。分数阶PID控制模块如图8所示。
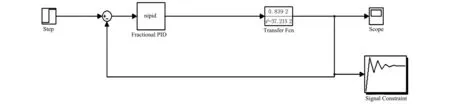
图7 环形倒立摆分数阶PID控制Matlab仿真结构
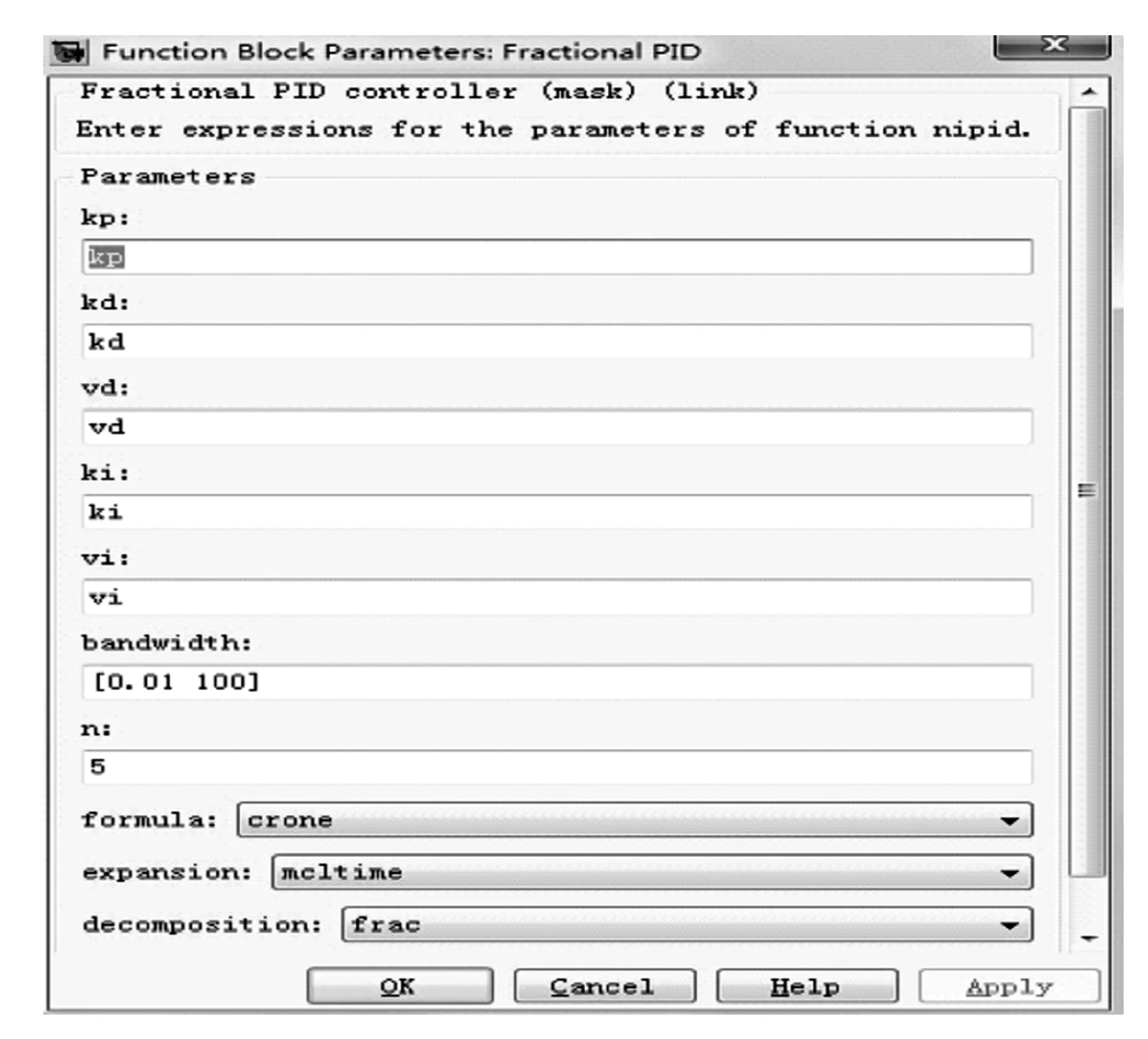
图8 分数阶PID控制模块
双击SignalConstraint模块,打开该模块的时域性能约束窗口。然后,在时域性能约束窗口中打开设置响应特性约束参数的窗口,把它的约束条件设置成与整数阶一样:上升时间为1s,调整时间为2s,最大超调量为5%,其余参数采用默认值。
在系统模型窗口中,加入封装好的分数阶PID控制模块,打开该模块的参数对话框,在比例系数(kp)、积分系数(ki)、微分系数(kd)、积分项阶数(vi)和微分项阶数(vd)等5个对话框中分别输入kp、ki、ld、vi、vd,按【OK】键后,在Matlab窗口中对分数阶PID控制器的初始值进行设置。设置完成后,系统即开始进行优化。得到的优化结果如图9所示。
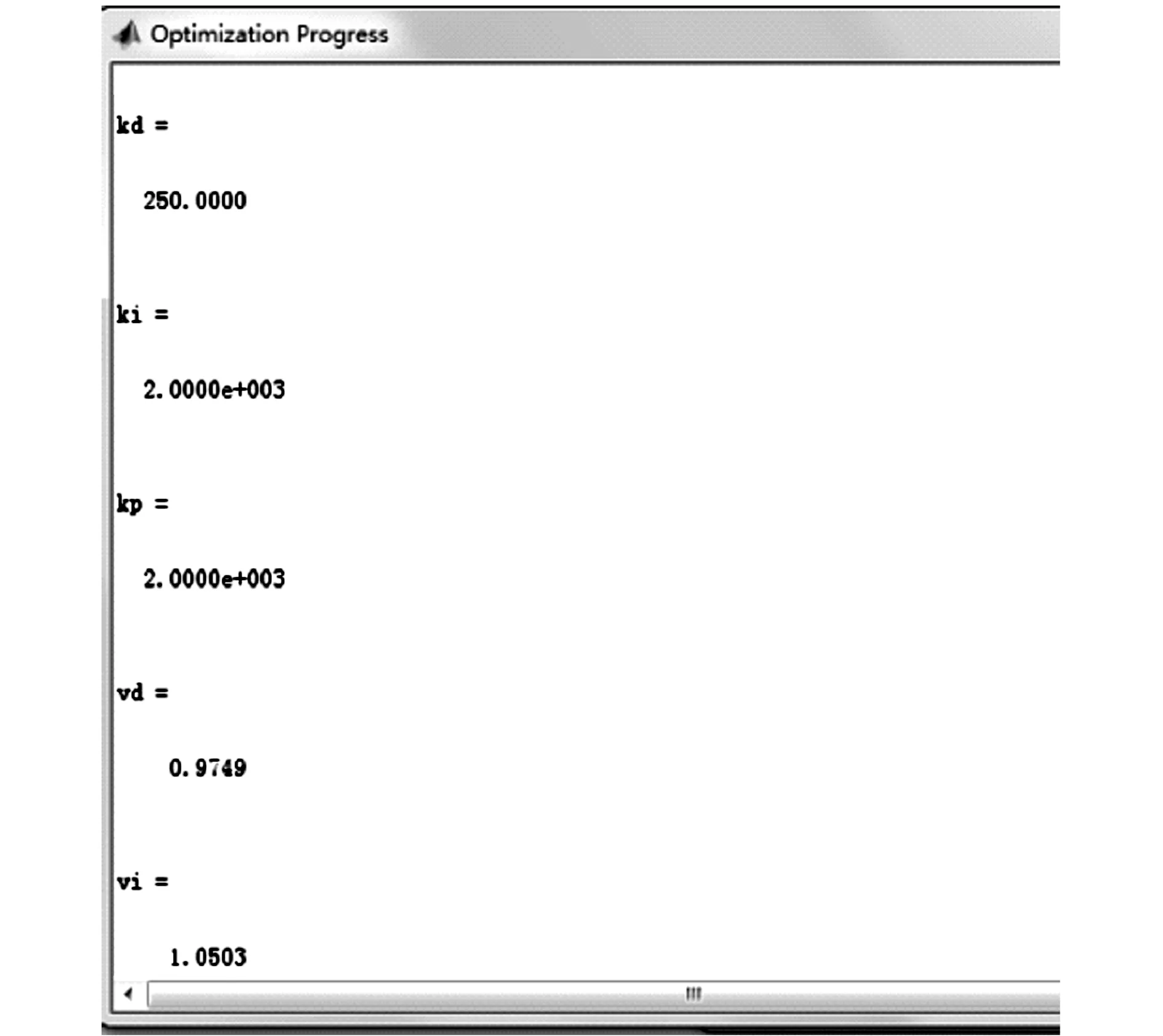
图9 分数阶PID优化结果
3 控制效果对比
根据优化结果报告得到的参数进行仿真,分别得到整数阶PID的仿真结果(见图10)和分数阶PID的仿真结果(见图11)。
将优化后的整数阶PID控制系统的输出响应曲线和分数阶PID控制系统的输出响应曲线局部放大(见图12)并进行对比,可以看出,在相同约束条件下,分数阶PID的上升时间、调节时间都更快,超调量相对较小,控制效果更好。
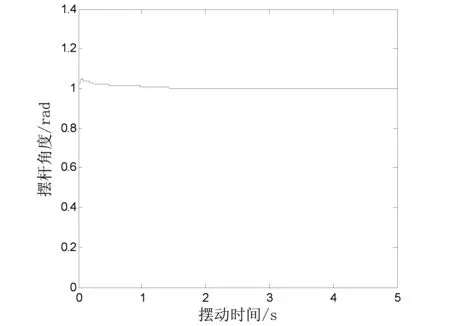
图10 环形单级倒立摆整数阶PID控制仿真结果

图11 环形单级倒立摆分数阶PID控制仿真结果

图12 整数阶PID和分数阶PID控制效果对比图
4 系统实现及实验结果
根据求出的倒立摆数学模型,运用Simulink搭建
环形单级倒立摆的系统模型,并将其封装。其实时控制模块如图13所示。
环形单级倒立摆的实时控制实验在MatlabSimulink环境中进行。打开倒立摆系统的实时控制模块,在分数阶PID控制模块中将分数阶PID控制器的参数输入(kp=2 000,ki=2 000,kd=250,vd=0.974 9,vi=1.050 3),然后点击编辑程序,编辑成功后点击“ConnectToTarget”,再点击“Startreal-timecode”,倒立摆摆杆摆起。环形单级倒立摆实时控制连杆和摆杆的输出波形分别见图14和图15。
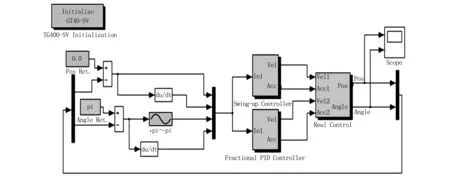
图13 环形单级倒立摆实时控制程序图
显然,在前7s内,倒立摆连杆由初始位置(0rad)小幅度均匀振荡,摆杆从初始位置(0rad)起摆至竖直方向(3.14rad)。摆杆起摆过程中发生较大幅度的振荡,持续时间约7s,之后稳定在竖直位置。摆杆起摆后,保持小幅度震荡,震荡幅度在±0.15rad以内。

图14 环形倒立摆实时控制连杆的响应曲线

图15 环形倒立摆实时控制摆杆的响应曲线
5 结 语
针对环形单级倒立摆系统,本文利用SignalConstraint优化模块分别对整数阶PID和分数阶PID进行优化设计。对它们的控制效果进行对比,结果表明,相对于整数阶的PID控制,分数阶PID控制多出2个控制参数,控制器的参数整定范围变大,控制器能够更灵活地控制倒立摆,可以得到更好的控制效果。本文设计的分数阶PID优化控制系统的倒立摆起摆迅速,稳定控制性能优良,上升时间和调节时间短,超调量小。
[1]PujolG,AchoL.StabilizationoftheFourthPendulumwithBacklashUsingH-LMITechnique:ExperimentalValidation[J].AsianJournalofControl, 2010, 12(4):460-467.
[2]NohJS,LeeGH,JungS.PositionControlofaMobileInvertedPendulumSystemUsingRadialBasisFunctionNetwork[J].InternationalJournalofControl,AutomationandSystems, 2010, 8(1):157-162.
[3]SooyongJ,WenJT.NonlinearModelPredictiveControlfortheSwing-upofRotaryInvertedPendulum[J].JournalofDynamicSystems,Measurement&Control, 2004, 126(3): 666-674.
[4]CastilloTB,ObregonPG,EspinosaGO.StructurallyStableRegulationforaClassofNonlinearSystems:ApplicationtoaRotaryInvertedPendulum[J].JournalofDynamicSystems,Measurement&Control, 2006, 128(4):18-19.
[5]PodlubnyI.Fraction-orderSystemsandControllers[J].IEEETransactionsonAutomaticControl, 1999, 44(1):208-214.
[6] 张晓华.控制系统数字仿真与CAD(第二版)[M].北京:机械工业出版社,2005:207-217.
[7] 赵文峰.控制系统设计与仿真[M].西安:电子科技大学出版社,2002:102-126.
[8] 赵春娜,李英顺,陆涛.分数阶系统的分析与设计[M].北京:国防工业出版社,2011:3-5.
(责任编辑:王长通)
Fractional PID Based Stability Control for Rotary Inverted Pendulum
LIAO Wu-dai, LIU Zheng-bo, WEN Sheng-jun, ZHANG Xiang-ming
(Zhongyuan University of Technology, Zhengzhou 45007, China)
In order to realize the stability control of the rotary inverted pendulum,a fractional order PID based optimal control is proposed.The mathematical model is firstly derived from Lagrange Equation ,which is a 3DOF under actuated system.The fractional order PID is considered for the system, where the parameters of the PID controller are optimized by Signal Constraint optimization module. Comparing with the integer order PID controller,it shows that the rotary inverted pendulum using fractional order PID controller is more quickly swigged up, and the setting time is shorter.
rotary inverted pendulum; Signal Constraint optimization module; fractional PID controller
2015-01-04
廖伍代(1963-),男,湖北武汉人,教授,博士,主要研究方向为系统工程、非线性控制、智能控制、神经网络理论与应用。
1671-6906(2015)06-0015-06
TP393
A
10.3969/j.issn.1671-6906.2015.06.004
