土体力学特性颗粒尺度效应的理论与试验研究

冯德銮，房营光, ，侯明勋

（1.华南理工大学 土木与交通学院，广东 广州 510641；2. 华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510641）

1 引 言

土体是由粒径跨越多个尺寸数量级的矿物颗粒以及水和空气在一定条件下聚集而成的不均匀不连续颗粒材料[1]，具有非常复杂的颗粒物质力学特性[2]。土体复杂的颗粒物质力学特性宏观上表现为不同尺度土颗粒对其强度和变形影响产生强烈的颗粒尺度效应。土体内部存在大量随土颗粒尺寸减小而增加的界面，土颗粒内部与土颗粒界面的力学性质完全不同，土颗粒内部过渡到界面的变形是不均匀不连续的，即土颗粒的尺寸和级配对土体内部的微细观变形特性有重要影响[3]，导致其在受力变形过程中表现出一系列与土颗粒尺寸直接相关的复杂力学行为[4]。土体中微颗粒主要产生由分子键引起的黏聚效应，而相对较粗颗粒则主要产生由接触键引起的摩擦效应，土体不同尺度颗粒间的多种微细观耦合力场对土体的强度和变形产生重要影响，即土体的宏观力学特性与其颗粒特征密切相关，突显土体强烈的颗粒尺度效应[5]。颗粒尺度效应可引起主要作用力的不同，导致材料內禀性能及其规律和原理的质的区别。经典土力学视土体为均匀连续介质，其理论基础仅建立在单一的宏观尺度之上，不能模拟和预测土体的颗粒尺度效应。因此，经典土力学在分析与土颗粒尺度有关的力学行为如剪切带[6]及泥石流[7]等的产生和发展的物理机制时遇到极大的挑战。随着离散元法的提出[8]和不断改善[9]，推动了土体颗粒尺度效应的模拟研究，并取得了一定的进展，但主要研究对象为同一尺度颗粒聚集而成的简单颗粒体系，且由于离散元法计算量过于庞大，计算模型以及模型参数难以确定，导致其在土体颗粒尺度效应模拟和工程实际计算中受到巨大的限制。

目前偶应力理论[10－12]被有效地应用于单相金属[13－14]和层状岩体[15－16]的尺度效应研究，但土体介质的颗粒性特征与金属材料的晶体性特征和层状岩体的节理性特征均有着本质的区别，能否有效地应用偶应力理论解释土体强度和变形的颗粒尺度效应，需要进一步的研究。Műhlhaus等[17]对偶应力理论在砂土中的应用做了开创性的工作，并假设內禀尺度为砂颗粒的平均粒径，但未对其物理意义作出解释。Fang[18]基于土体不同尺度颗粒间相互作用产生的物理力学效应，提出了基于偶应力理论的“基体-加强颗粒”土体胞元模型，并通过一系列的三轴试验，初步验证了屈服应力的模型预测与试验结果的一致性，但文中仅把加强颗粒视为具有相同粒径的球体并未考虑其级配对屈服应力理论计算结果的影响，且未对模型中的应变梯度和內禀尺度等反映土体颗粒尺度效应的微细观参数作出定量计算和物理机制分析。

本文基于土体胞元理论模型，进一步提出基于颗粒间相互作用产生黏聚和摩擦的物理效应而非纯粹几何尺寸作为划分颗粒尺度层次的依据，划分胶结性的黏聚颗粒和耗散性的摩擦颗粒构造可反映土体内部材料信息和颗粒特征信息的细观土体胞元，建立考虑加强颗粒级配的胞元土体理论；采用多种颗粒组合制备胞元土体理论的饱和重塑土试样，进行一系列三轴不固结不排水剪切试验，对土体力学特性的颗粒尺度效应进行测定，同时定量计算胞元土体理论中反映土体内部不均匀不连续变形的应变梯度和反映土体颗粒尺度效应的內禀尺度，并解释其物理意义。

2 胞元土体理论模型

2.1 胞元土体理论物理力学基础

土体颗粒的粒径跨越多个尺寸数量级，颗粒间的连结作为土体颗粒各种粒间力相互作用的综合反应，对土体的宏观力学特性产生直接影响[19]。土体颗粒间的连结形态通常是分子键联结和接触键连接并存。比表面积和表面电位是土颗粒产生分子键联结还是接触键连接的决定因素，土体中微颗粒由分子键联结，主要表现为黏聚效应，体现范德华力和库仑力等微观力场的相互作用。相对较粗颗粒则由接触键连接，主要表现为摩擦效应，体现重力和外部荷载等宏观力场的相互作用。上述由土颗粒尺寸决定的连结方式对土体的宏观变形和强度特性产生重大影响。研究发现[20]，颗粒间的黏聚和摩擦效应与颗粒间的微观作用力(范德华力、库仑力等)与颗粒重力的比值(简称为微重比)有密切关系，引入微重比作为衡量颗粒间黏聚和摩擦效应以及划分颗粒尺度的判别参数，依此确定颗粒间产生黏聚效应和摩擦效应的颗粒界限尺寸。对于石英颗粒，其颗粒表面电荷密度经阳离子交换试验实测为9 419.5静电单位/平方厘米，Hamaker常数为8.86×10-20J，根据表面化学原理，图1为两个石英颗粒间的范德华力和库仑力与其重力之间的比值随颗粒粒径变化的计算曲线。图中，Fw为范德华力；Fe为库仑力；W为重力。

图1 颗粒间微观作用力与重力比值关系Fig. 1 Relationships between micro-forces and gravity

从图1中可以看出，当颗粒粒径较小时，颗粒间的相互作用力主要体现为微观作用力，随着颗粒粒径增大，重力作用效应逐步显现。为定量探究土体的颗粒尺度效应，根据土颗粒间的连结性状及微重比，按不同的尺度层次以粉粒粒径（75 μm）为界，将土体的固相部分划分为以产生黏聚效应为主的基体颗粒和以产生摩擦效应为主的加强颗粒，其中粒径小于粉粒的颗粒称为基体颗粒，粒径大于粉粒的颗粒称为加强颗粒，基体颗粒通过与孔隙水和气体相结合形成均匀连续的团聚体（基体），加强颗粒假设为球体并均匀分布于基体中，且为基体所包裹。基体与包裹于其内的加强颗粒共同构成土体的土体胞元，土体胞元为土体的基本单元，如图2所示。宏观土体则由一系列胞元聚集而成，由此把土体简化为具有胞元结构的颗粒物质。胞元土体模型可考虑黏性土不同尺度颗粒之间相互作用产生的黏聚效应和摩擦效应。

图2 土体胞元结构Fig.2 Soil cell element

2.2 胞元土体理论分析

根据土体不同尺度结构层次上力学响应的特征，土体可划分为宏观、细观和微观3个不同尺度的结构层次，如图3所示。

图3 土体介质多尺度研究框架Fig.3 The multiscale framework of soil

土体在受力变形过程中，微观上表现为土颗粒间的连接件(分子键和接触键)的滑移和拉裂；细观上表现为土体胞元因两相介质(基体和加强颗粒)变形性状差异诱发内部材料形状畸变而产生应变梯度；宏观上表现为土体非线性，剪胀性和应变软化等复杂的工程力学行为。因此，土体在不同尺度层次上的力学行为是不一致的，土体胞元作为反映土体内部材料信息和颗粒特征信息的基本单元，成为建立连接多个耦合尺度的多尺度理论框架的纽带。从细观角度考虑，在外部荷载作用下基体产生连续变形，加强颗粒产生平移和转动，基体与加强颗粒因变形性状差异而引发土体胞元内部的不协调变形，表现为加强颗粒邻近基体应变的梯度现象。Fang[18]基于偶应力理论和能量平衡原理，得到了三轴不固结不排水条件下不考虑加强颗粒级配的土体胞元模型屈服应力和应变梯度表达式：

2.3 考虑加强颗粒级配的土体胞元模型理论计算

联立式（2）和式（3）可以定量地计算考虑加强颗粒级配的应变梯度：

应变梯度是土体内部不均匀不连续变形的综合反应，与加强颗粒的体分比和粒径有关。

2.4 內禀尺度le计算

內禀尺度是反映土体颗粒尺度效应的特征参量，由式（1）、（5）可得

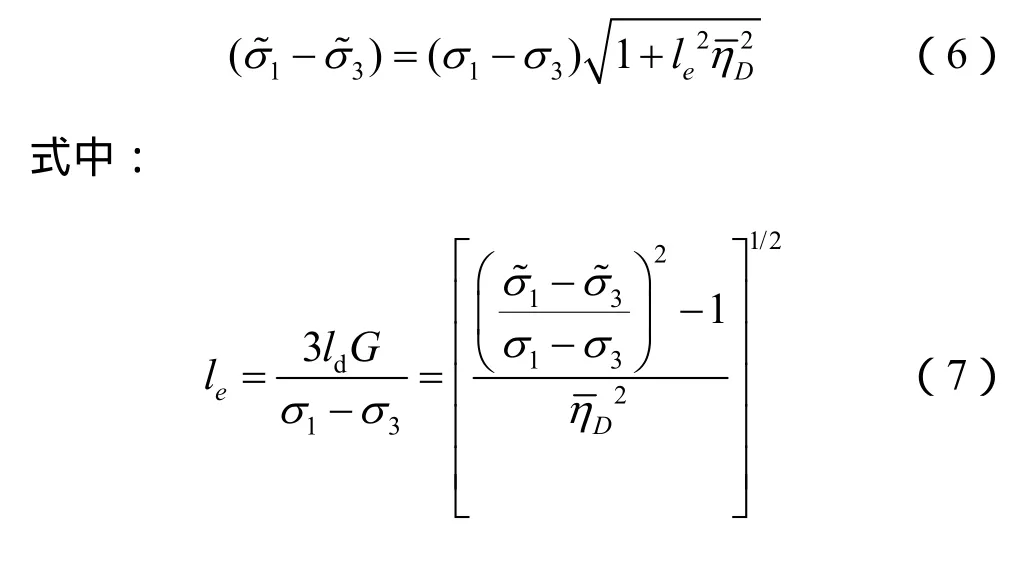
式中：le为土体胞元的內禀尺度，与加强颗粒的体分比和粒径有关，可由式（7）定量计算。

由式（6）、（7）可知，胞元土体理论揭示土体的屈服应力与应变梯度、內禀尺度以及加强颗粒的粒径和体分比有关，可较好地反映土体的颗粒尺度效应。

3 胞元土体理论三轴不固结不排水剪切试验

3.1 试验材料与方案

试验采用广州重塑黏土颗粒作为基体颗粒，高纯度商用石英砂作为加强颗粒。根据章节2.1的分析，筛分得到体现黏聚效应的粒径小于 0.075 mm的黏土颗粒作为基体颗粒。选取体现摩擦效应的粒径相对较大的商用石英砂作为加强颗粒，经筛分选择2个粒径组合，分别为0.1～0.3 mm和0.5～0.9 mm。试验材料的基本物理参数见表1。

采用多种加强颗粒组合制备胞元土体理论的饱和重塑土试样以进行一系列的三轴不固结不排水剪切试验。基体性质通过基体含水率（基体液性指数）控制。

表1 试验材料的基本物理参数Table 1 Basic physical parameters of experiment materials

制备试样时，先在黏土颗粒中掺入石英砂颗粒进行充分搅拌，再掺入适量水进行长时间搅拌，保证加强颗粒均匀分布于基体之中，掺入的石英砂颗粒作吸湿处理，保证其掺入后不改变基体的含水率。同时，试样经真空抽气饱和处理达到饱和状态。试样尺寸为直径为39.1 mm，高80 mm。同一系列试样具有相同的基体含水率。

采用全自动应变控制式三轴仪对试样进行三轴不固结不排水剪切试验，剪切速率为应变1%/min。试验过程中，设定基体液性指数Il=0.2(硬塑)和Il=0.4(可塑)，设定加强颗粒的体分比α为 0、0.088、0.162和0.225，加强颗粒粒径d为0.1～0.3 mm和0.5～0.9 mm，设定每组试验的围压P为100、200、300 kPa。制备48件试样，共进行了16组试验，均按《土工试验规程》[21]进行。

3.2 试验结果

对于三轴不固结不排水试验，试验过程中试样始终不允许排水，其体积保持不变，即试样剪切前不同围压下的有效应力不变，则不同围压下试样的应力-应变曲线理论上一致，可将同一组别不同围压下的试验看作是一组平行试验，并以同一条曲线表示其应力-应变关系，试样的应力-应变关系如图 4所示。

4 试验结果分析及物理机制的解释

4.1 试验结果分析

图4为试样三轴不固结不排水剪切试验的应力-应变曲线的测试结果。利用这些随试样加强颗粒粒径和体分比改变而改变的三轴试验结果，可对土体力学特性的颗粒尺度效应进行分析。从图中可以看出，当轴向应变较小时，轴向应力随轴向应变的增加而迅速增加，加强颗粒对试样的应力-应变关系影响不明显；随后，轴向应力随轴向应变增加的速度逐渐减缓而进入屈服阶段，且试样的屈服应力随加强颗粒粒径和体分比的变化而明显改变，当加强颗粒粒径不变时，试样的屈服应力随加强颗粒体分比的增加而明显增加；当加强颗粒体分比不变时，试样的屈服应力随加强颗粒粒径的减小而明显增加。加强颗粒的粒径减小和体分比增加均使试样的应力-应变曲线得到强化。上述的土体抗剪强度特性随颗粒粒径和颗粒含量比例（体分比）变化而改变的现象，反映了其力学特性的颗粒尺度效应。

图4 试样的轴向应力-应变关系Fig.4 Relationships between axial stress-strain

4.2 颗粒尺度效应物理机制解释

由章节3给出的试样制备方法可知，加强颗粒随机分布于基体中且为基体所包裹，形成如图2所示的土体胞元。宏观试样则简化为由许许多多土体胞元集合而成的具有胞元结构的胞元土体。其中黏土颗粒与水相互结合形成反映黏聚效应的基体，石英砂颗粒则可视为反映摩擦效应的刚性加强颗粒，在轴向应力作用下基体产生均匀连续应变，加强颗粒不发生变形但产生刚体转动和平动。基体与加强颗粒变形性状的差异引发加强颗粒邻近基体产生应变集中，应变集中增强至一定程度时，细观上表现为土体胞元内部出现形状畸变而产生不可忽略的应变梯度，微观上表现为加强颗粒邻近基体产生协调微裂纹[4]以适应基体与加强颗粒两相介质间的不相容变形，如图5所示。当试样轴向应变较小时，加强颗粒导致其邻近基体的应变集中不明显，此时加强颗粒对试样的应力-应变关系影响不明显；随着轴向应变的增加，加强颗粒邻近基体的应变集中和应变梯度逐渐显著，土体力学特性的颗粒尺度效应趋于强烈。

由于应变梯度和协调微裂纹的出现，土体中的应变能由应变和应变梯度共同引起。加强颗粒转动使其邻近基体产生形状畸变而引起的微裂纹萌生，导致土体比均匀连续变形情况下储存或释放更多的能量，使其变形阻力增加，在宏观上体现出具有更强的变形性能和更高的屈服强度。

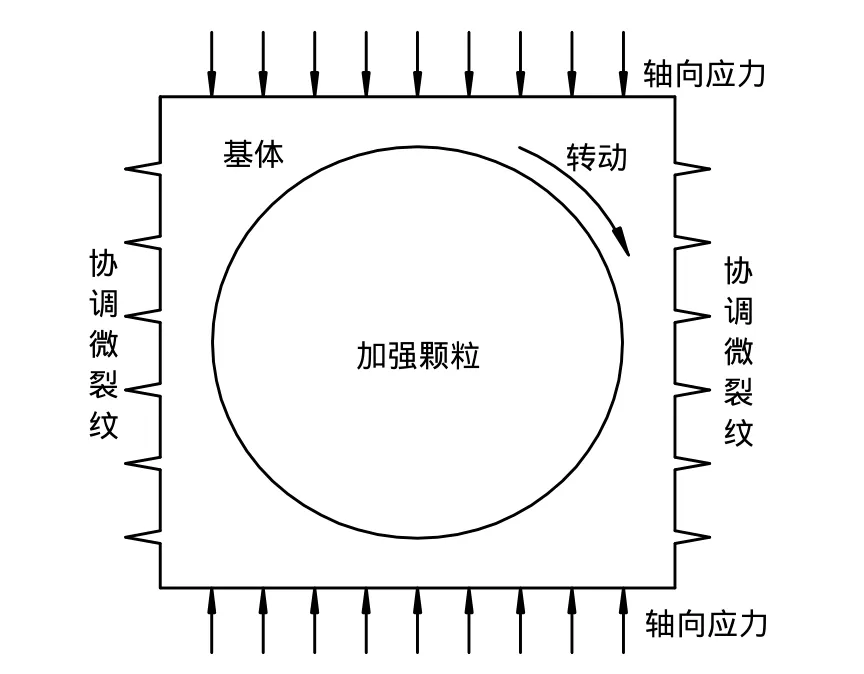
图5 加强颗粒邻近基体的协调微裂纹Fig.5 Coordinated microcracks around the matrix joined with the reinforcement particle

4.3 土体屈服应力理论值与试验值比较

由式（6）可知，根据土体的应变梯度和內禀尺度以及基体的应力-应变关系，可对含加强颗粒的土体的屈服强度进行预测，屈服应力预测结果的σth与试验结果的σte的对比见表2。

表2 土体屈服应力的理论值与试验值比较Table 2 Comparison of soil yield stress calculated by model in concert with the test results

由表2可见，胞元土体理论的理论值与试验值的相对误差不大于10%，考虑到制样过程中加强颗粒在土样中分布的随机性和不均匀性以及试验条件和假设条件对试验结果准确性的制约，胞元土体理论的预测结果总体上是可以接受的。

5 结 论

土体力学特性的颗粒尺度效应是土体微细观结构特征对其宏观力学响应产生影响的综合反应。加强颗粒的掺入致使原本的单相基体转变为物理力学性质差异巨大的基体-加强颗粒两相介质(土体胞元)，细观上诱发土体胞元内部出现形状畸变而产生应变梯度，微观上诱发加强颗粒邻近基体出现强烈的应变集中而产生协调微裂纹。土体颗粒尺度效应的物理机制可解释为：加强颗粒使其邻近基体产生不均匀不连续变形而引起的应变梯度和协调微裂纹，导致土体比均匀连续变形情况下储存或释放更多的能量，以使其变形阻力增加，在宏观上体现出具有更强的变形性能和更高的屈服强度。基于不同尺度土颗粒间相互作用产生的物理力学效应而建立的可考虑加强颗粒级配的土体胞元颗粒尺度效应屈服强度计算公式，初步验证了理论预测与试验结果的一致性。

[1] HERRMANN H J. Granular matter[J]. Physica A, 2002,313(1－2): 188－210.

[2] 史旦达, 周健, 刘文白, 等. 砂土直剪力学性状的非圆颗粒模拟与宏细观机制研究[J]. 岩土工程学报, 2010,32(10): 1557－1565.SHI Dan-da, ZHOU Jian, LIU Wen-bai, et al. Exploring macro- and micro-scale responses of sand in direct shear tests by numerical simulations using non-circular particles[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1557－1565.

[3] 尹振宇. 土体微观力学解析模型: 进展及发展[J]. 岩土工程学报, 2013, 35(6): 993－1009.YIN Zhen-yu. Micromechanics-based analytical model for soils: review and development[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 993－1009.

[4] 房营光, 冯德銮, 马文旭, 等. 土体介质强度尺度效应的理论与试验研究[J]. 岩石力学与工程学报, 2013,32(11): 2359－2367.FANG Ying-guang, FENG De-luan, MA Wen-xu, et al.Theoretical and experimental study on size effect of soil strength[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2359－2367.

[5] BAŽANT Z P. Size effect on structural strength: A review[J]. Archive of Applied Mechanics, 1999, 69(9－10): 703－725.

[6] ZHAO J, SHENG D, ZHOU W. Shear banding analysis of geomaterials by strain gradient enhanced damage model[J]. International Journal of Solids and Structures, 2005, 42(20): 5335－5355.

[7] IVERSON R M. The physics of debris flows[J]. Reviews of Geophysics, 1997, 35(3): 245－296.

[8] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assembles[J]. Geotechnique, 1979,29(1): 47－65.

[9] LI X, WAN K. A bridging scale method for granular materials with discrete particle assembly—Cosserat continuum modeling[J]. Computers and Geotechnics,2011, 38(8): 1052－1068.

[10] COSSERAT E, COSSERAT F. Théorie des corps déformables[M]. Paris：[s.n.], 1909.

[11] TOUPIN R A. Elastic materials with couple-stresses[J].Archive for Rational Mechanics and Analysis, 1962,11(1): 385－414.

[12] MINDLIN R D. Influence of couple-stresses on stress concentrations[J]. Experimental Mechanics, 1963, 3(1):1－7.

[13] FLECK N A, HUTCHINSON J W. A phenomenological theory for strain gradient effects in plasticity[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(12):1825－1857.

[14] 章定国, 吴胜宝, 康新. 考虑尺度效应的微梁刚柔耦合动力学分析[J]. 固体力学学报, 2010, 31(1): 32－39.ZHANG Ding-guo, WU Shen-bao, KANG Xin.Rigid-flexible coupling dynamic analysis of a micro beam considering size effect[J]. Chinese Journal of Solid Mechanics, 2010, 31(1): 32－39.

[15] 张敦福, 王相玉, 朱家明, 等. 偶应力对层状岩体结构面边界层效应的影响[J]. 岩石力学与工程学报，2012,33(7): 2181－2188.ZHANG Dun-fu, WANG Xiang-yu, ZHU Jia-ming, et al.Influence of couple stress on interfaces boundary layer effect of layered rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 33(7): 2181－2188.

[16] 张敦福, 王相玉, 李术才. 偶应力对含充填层状岩体边界层效应的影响[J]. 岩石力学与工程学报, 2011, 30(增刊1): 3287－3294.ZHANG Dun-fu, WANG Xiang-yu, LI Shu-cai. Influence of couple stress on interfaces boundary layer effect of layered rock mass with inclusion[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Supp.1):3287－3294.

[17] MŰHLHAUS H B, VARDOULAKIS I. The thickness of shear band in granular materials[J]. Geotechnique, 1987,37(3): 271－283.

[18] 房营光. 土体强度与变形尺度特性的理论与试验分析[J].岩土力学, 2014, 35(1): 41－47.FANG Ying-guang. Theoretical and experimental investigation on size effect characteristic of strength and deformation of soil[J]. Rock and Soil Mechanics, 2014,35(1): 41－47.

[19] MITCHELL J K, KENICHI S. Fundamentals of soil behavior(third edition)[M]. New York：John Wiley &Sons, Inc, 2005.

[20] 房营光. 颗粒介质尺度效应的抗剪试验及物理机制分析[J]. 物理学报, 2014, 63(3): 274－283.FANG Ying-guang. Shear test and physical mechanism analysis on size effect of granular media[J]. Acta Physica Sinica, 2014, 63(3): 274－283.

[21] 南京水利科学研究院. GB/T 50123－1999土工试验方法标准[S]. 北京: 中国建筑工业出版社, 2000.