饱和软土层地铁列车运行引起的环境振动研究

黄 强 ，黄宏伟 ，张 锋，叶 斌 ，张冬梅

（1. 同济大学 地下建筑与工程系，上海 200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海 200092；3. 日本国立名古屋工业大学 都市社会工学科，日本 名古屋 466-8555）

1 引 言

我国沿海发达地区的大量地铁都修建在饱和软黏土地层，这些土层大多属于第四系沉积层土，含水率大、压缩性高、渗透系数小，在地铁列车振动作用下易受到扰动而发生变形，因而地铁列车运行引起的环境效应日益受到社会关注。地铁线路常穿越城市中心，地表高楼林立或是居民区分布，地铁列车引起的振动将直接影响地表建筑物的安全，居民生活环境的舒适度[1]。另一方面，地铁振动引起的下卧土层超孔隙水压力响应研究还不够，饱和土中孔隙水压力的变化直接影隧道的沉降，因此，有必要分析列车振动引起的孔隙水压力响应规律。

在地铁列车引起的环境振动规律研究方面，国内外学者大多采用数值计算方法，包括有限元[2－4]、边界元[5－6]和 2.5 维等[7－8]。由于动力问题的复杂性，国内外学者研究列车运行引起的环境振动问题时往往将土体考虑为单相弹性介质，鲜有考虑饱和地层的情况。沿海地区修建的地铁隧道大多处在饱和土软土层中，用单相介质无法反映振动荷载作用下土体孔隙水压力的变化，也无法反映孔隙水压力存在对周围环境动力响应的影响。

本文对饱和土层中地铁列车振动引起的环境振动响应分析主要体现在两方面：一是分析地表振动加速度及最大位移响应，从而确定地表的振动强度；二是分析列车行驶时隧道下卧土层的超孔隙水压力响应及列车驶离后累积超孔隙水压力。通过和干土数值结果比较，指出饱和土振动响应的差异。

2 列车振动荷载的确定

英国铁路技术中心根据多年的大量理论与实验工作表明产生竖向轮轨力的主要原因是各种不平顺及周围局部扁疤等因素造成的，竖向荷载可以用一个激振力函数来模拟[9]，其表达式为

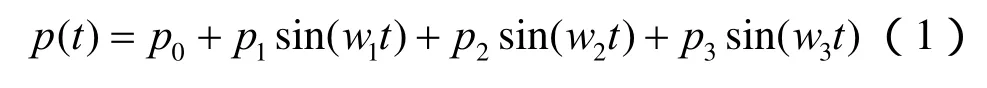
式中：p0为车轮静载；p1、p2、p3分别为几何不平顺Ⅰ、Ⅱ、Ⅲ控制条件对应的振动荷载。具体的计算及相关参数详见文献[9]。

由于列车振动荷载作用在铁轨上，通过铁轨传递至道床，再传递到隧道上。因此，可以近似假定荷载沿着隧道纵向均匀分布[10]，故作用在道床上的列车荷载为

式中：n为单节列车轮对数；L为列车长度（m）。

8节编组地铁列车时速80 km/h下荷载时程曲线如图1所示。

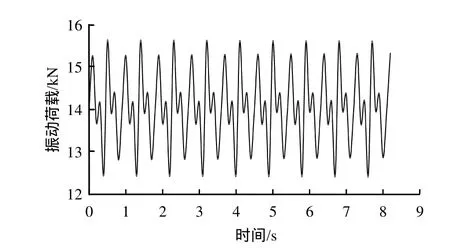
图1 列车荷载时程曲线（v = 80 km/h）Fig.1 Time-history curve of train vibration load at v = 80 km/h

3 计算模型及理论

以上海地铁2号线某区间隧道为例，建立平面模型，考虑到隧道结构的对称性，取1/2模型进行分析，计算模型如图2所示。

图2 有限元计算模型Fig.2 Finite element model

盾构隧道的外径为6.2 m，内径为5.5 m，隧道中心埋深15.0 m，申跃奎[11]对上海地铁激励下的振动规律进行了研究，认为上海土的波长sλ可按70 m考虑，模型尺寸满足(1.0～1.5)sλ的计算范围即可，因此模型宽93 m(15D)，深80.6 m(13D)，考虑到振动衰减，侧边界可为水平向变形约束，竖向自由边界，场地底部为固定边界；地表为自由边界。地表及右侧边界设为排水边界，由于上海地下水位较高，这里假定土层都处于饱和状态。模型中饱和土层的分布从上到下编号及参数信息见表2。

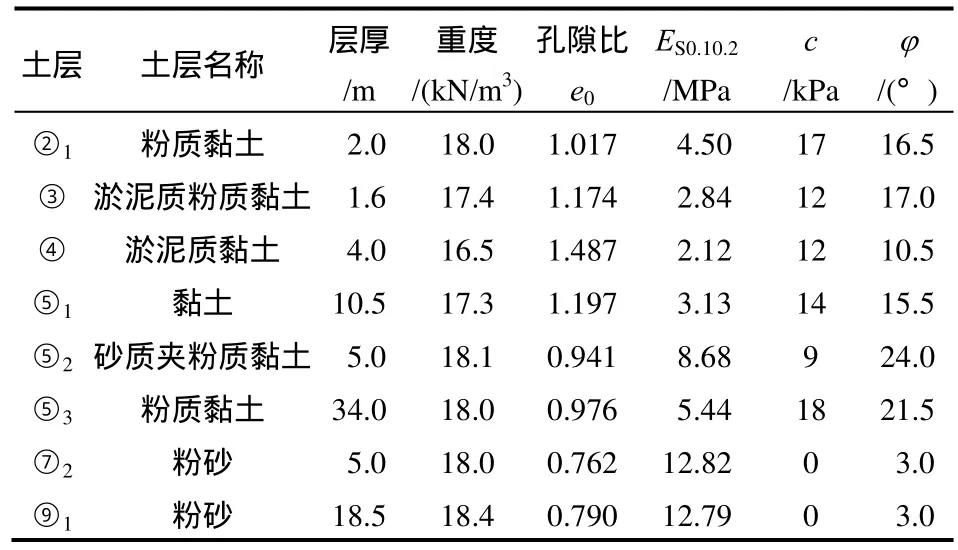
表2 土层参数Table 2 Soil parameters

3.1 土体本构模型

本文采用 Zhang等[12]提出的 cyclic mobility model，此本构模型是上、下负荷屈服面基础上，并引入了应力引起的各向异性概念，可以统一描述交变加载和单向加载条件下饱和砂性土和黏性土的排水和不排水特性。

cyclic mobility model屈服面方程为

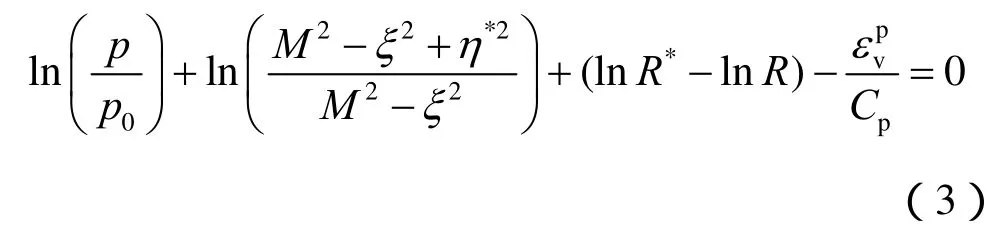
本构模型除了能反映土体卸载再加载过程中土体塑性变形累积特性外，还反映土体的超固结、结构性和应力引起的旋转硬化特征，这些特征对循环荷载下土体的变形有重要影响。

3.2 土-水耦合有限元方法

对于饱和软土，采用有效应力法分析时，需要考虑土-水耦合作用。这里采用Oka等[13]提出的二相混合体理论，采用u-p形式方程来描述。二相混合体理论的控制方程如下：

平衡方程：

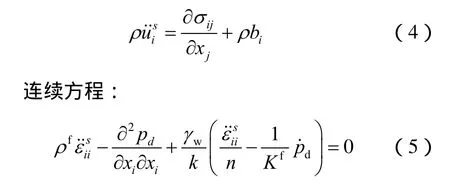
式中：ρf为液相密度；pd为动的超孔隙水压力；γw为液相的重度；k为土体的渗透系数；n为土体孔隙率；fK 为液相压缩模量。

4 计算结果及分析

4.1 地表最大振动加速度响应

采用动力有限元的方法计算了饱和软土层地表竖向最大振动加速度，同时对比干土的振动规律。用加速度振级 La来衡量地表振动强度，计算公式为

图5、6分别为地表水平向和竖直向的最大加速度和振级（v = 80 km/h）。从图中可以看出，饱和土和干土的地表动力响应存在明显的区别。首先，饱和土的地表振动加速度响应要比干土小得多。其次，地表水平向与竖向振动加速度响应规律存在明显的不同。干土地表水平振动加速度存在两个放大区，分别在离隧道中心30 m和40 m位置处，竖向振动存在一个振动放大区，在地表20 m处，与文献[2]结论一致，但饱和土的竖向加速度不存在振动放大区，随距离增加而快速衰减，水平加速度在离开隧道中心10 m后达到峰值，随后逐渐衰减，也没有出现振动放大区，说明饱和软土层的振动响应和单相介质下的振动特性有明显不同。

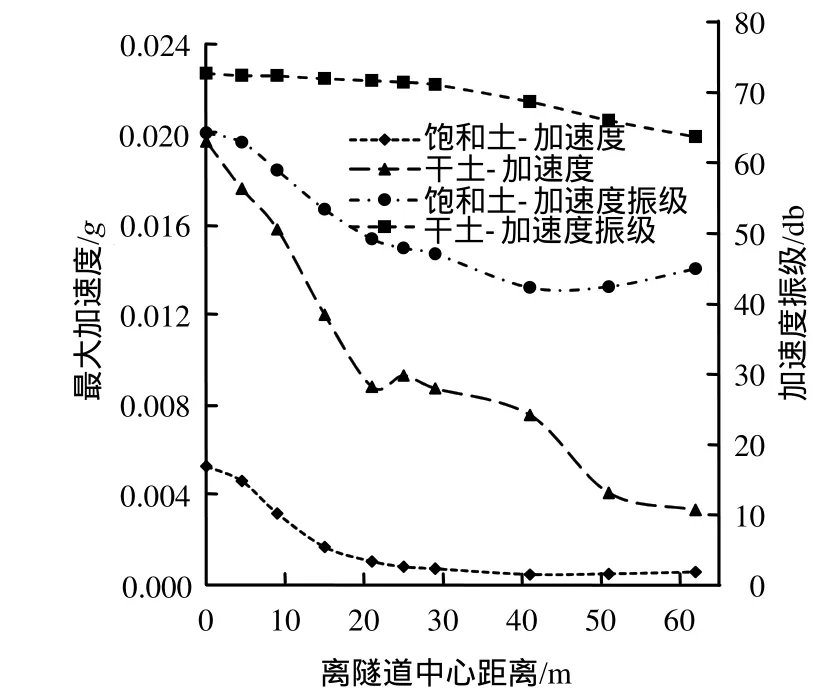
图5 饱和土与干土地表竖向最大加速度与振级（v = 80 km/h）Fig.5 Maximum vertical vibration acceleration and acceleration level of ground surface between saturated soil and dry soil (v = 80 km/h)

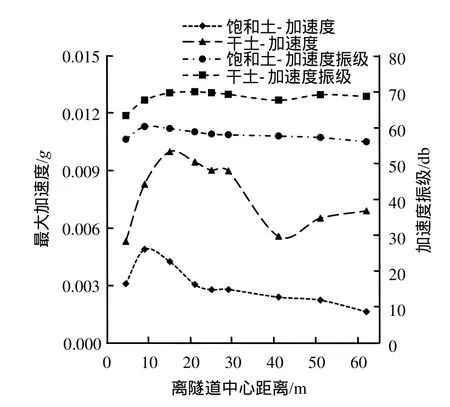
图6 饱和土与干土地表水平向最大加速度与振级（v = 80 km/h）Fig.6 Maximum horizontal vibration acceleration and acceleration level of ground surface between saturated soil and dry soil (v = 80 km/h)

4.2 地表最大振动位移响应

图7比较了饱和软土地表水平向和竖直向的最大振动位移以及加速度振级（v = 80 km/h）。离开隧道中心10 m后，地表的水平向振动加速度和加速度振级都大于竖向值，表明地表振动从竖向振动为主转向以水平方向向为主；在距离隧道中心 25 m处，地表竖向和水平向振动位移存在一个放大区，地表振动位移随着距离振源的增加有所增加，但幅度很小。

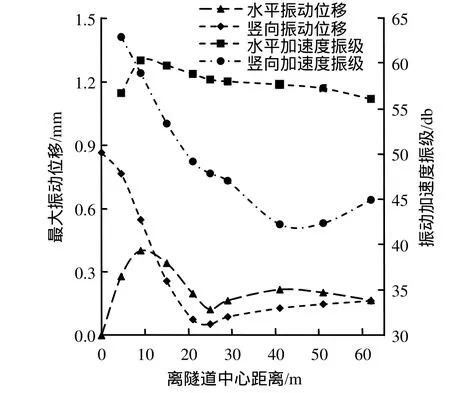
图7 饱和土地表竖向与水平向最大振动位移与振级（v = 80 km/h）Fig.7 Maximum vertical and horizontal vibration displacement and acceleration level of ground surface between saturated soil and dry soil (v = 80 km/h)

4.3 饱和土超孔隙水压力响应

选取隧道下方0.5、5.0、10.0 m深度且离隧道中心0、9、21 m处的单元，分析超孔隙水压力响应规律，单元位置见图8。

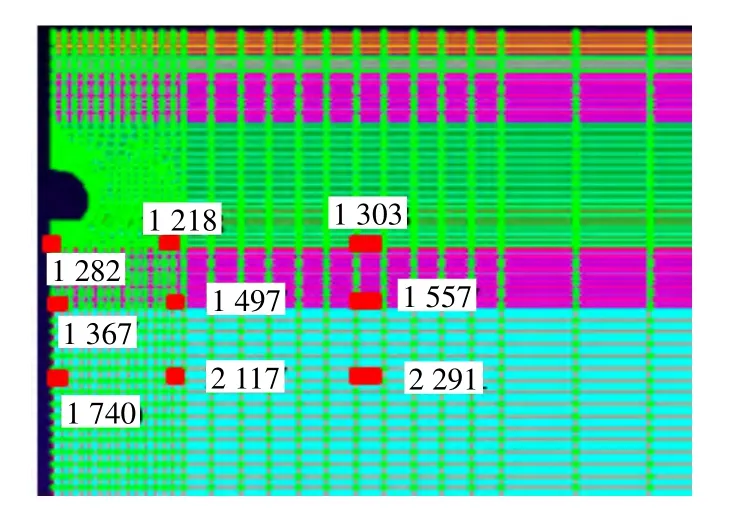
图8 超孔隙水压力分析单元示意图Fig.8 Sketch of excess pore water pressure elements

计算结果表明，隧道下方不同深度的超孔隙水压力沿水平向都是不断衰减的，以隧道下方 0.5 m处超孔隙水压力分布为例，如图 9所示。另一方面，距隧道水平距离相同时超孔隙水压力沿深度方面上响应有所不同。从图10(a)可以看出，在振源正下方方向，超孔隙水压力随深度增加快速衰减，表现为衰减趋势；在距隧道中心9、21 m的纵断面如图 10(b)、10(c)所示。一定范围内超孔隙水压力随着深度的增加而增加，说明在远离隧道中心的纵断面上，超孔隙水压力是先增加后减少的趋势，表明隧道下方的土层以竖向振动为主，超孔隙水压力沿水平向比竖向衰减的更快。

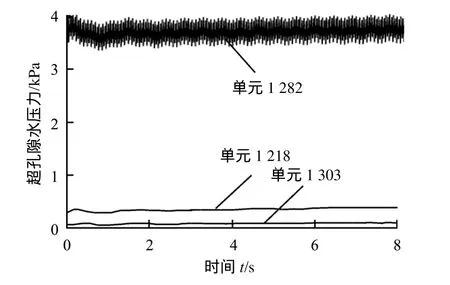
图9 横向超孔隙水压力分布（隧道底下方0.5 m）Fig.9 Horizontal distribution of EPWP(at depth 0.5 m below bottom of tunnel)

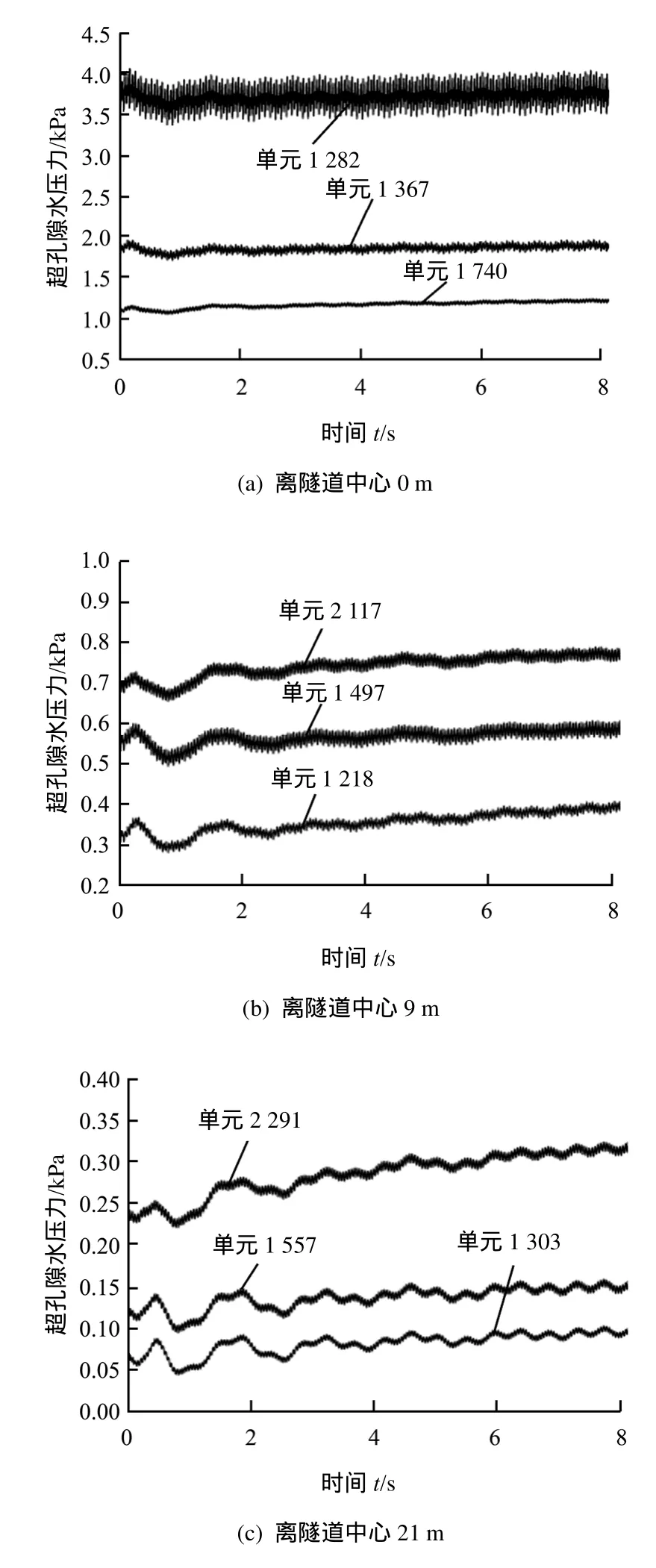
图10 竖向超孔隙水压力分布Fig.10 Vertical distribution of excess pore water pressure

5 结 论

（1）饱和软土中地铁列车运行产生的地表振动与干土有明显的不同。饱和土层的地表最大振动位移、最大振动加速度以及相应的振级都比干土的响应值小得多，干土振动沿地表传播时振动加速度存在振动放大区，而饱和土振动加速度沿地表不存在放大区。

（2）饱和土的水平振动响应与竖向振动响应不相同。水平最大振动加速度响应是先增加后减少，在10 m达到峰值，竖向振动加速度则是一直递减，衰减速度先快后慢，距隧道中心超过10 m后地表的振动位移以水平振动为主，且在25 m处存在一个振动位移放大区。

（3）饱和土在列车振动荷载作用会产生超孔隙水压力。水平断面上超孔隙水压力随着离隧道中心距离增加而衰减，越接近隧道断面，水平向地衰减越快；纵断面上隧道正下方的超孔隙水压力随深度增加而减少，在其他纵断面上超孔隙水压力则是随深度先增加后减少。

[1] 陈国兴, 苏晓梅, 陈斌. 地铁列车运行引起的环境振动评价[J]. 防灾减灾工程学报, 2008, 28(1): 70－74.CHEN Guo-xing, SU Xiao-mei, CHEN Bin. Evaluation of ambient vibration induced by passing trains in subway tunnel[J]. Journal of Disaster Prevention and Mitigation, 2008, 28(1): 70－74.

[2] 刘维宁, 夏禾, 郭文军. 地铁列车振动的环境响应[J].岩石力学与工程学报, 1996, 15(增刊1): 586－593.LIU Wei-ning, XIA He, GUO Wen-jun. Study of vibration effects of underground trains on surrounding environments[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(Supp.1): 586－593.

[3] 白冰, 李春峰. 地铁列车振动作用下交叠隧道的三维动力响应[J]. 岩土力学, 2007, 28(增刊1): 715－718.BAI Bing, LI Chun-feng. Three-dimensional elastic dynamics response of close crisscross tunnels subjected to subway loading[J]. Rock and Soil Mechanics, 2007,28(Supp.1): 715－718.

[4] 张波, 李术才, 张敦福, 等. 岩石介质中地铁列车运行引起的环境振动响应研究[J]. 岩石力学与工程学报,2011, 30(增刊 1): 3341－3347.ZHANG Bo, LI Shu-cai, ZHANG Dun-fu, et al. Research on rock environments vibration response induced by metro trains in rock media[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Supp.1): 3341－3347.

[5] GUPTA S, LIU W F, DEGRANDE G, et al. Prediction of vibrations induced by underground railway traffic in Beijing[J]. Journal of Sound and Vibration, 2008,310(3): 608－630.

[6] CLOUTEAU D, ARNST M, AL-HUSSAINI T M, et al.Freefield vibration due to dynamic loading on a tunnel embedded in a stratified medium[J]. Journal of Sound and Vibration, 2005, 283(1－2): 173－199.

[7] YANG Y B, HUNG H H. A 2.5D finite/infinite element approach for modelling viscoelastic bodies subjected to moving loads[J]. International Journal for Numerical Methods in Engineering, 2001, 51(11): 1317－1336.

[8] YANG Y B, HUANG H H, CHANG D W. Train-induced wave propagation in layered soils using finite/infinite element simulation[J]. Soils Dynamics and Earthquake Engineering, 2003, 23(4): 263－278.

[9] JENKINS H H, STEPHENSON J E, CLAYTON G A,et al. The effect of track and vehicle parameters on wheel/rail vertical dynamic forces[J]. Railway Engineering Journal, 1974, 3(1): 2－16.

[10] 李德武. 列车振动荷载的数定分析[J]. 甘肃科学学报,1998, 10(2): 25－29.LI De-wu. A deterministic analysis of dynamic train loading[J]. Journal of Gansu Science, 1998, 10(2): 25－29.

[11] 申跃奎. 地铁激励下振动的传播规律及建筑物隔振减振研究[博士论文D]. 上海: 同济大学, 2007.

[12] ZHANG F, YE B, NODA T, et al. Explanation of cyclic mobility of soils: approach by stress-induced anisotropy[J]. Soils and Foundations, 2007, 47(4): 635－648.

[13] OKA F, YASHIMA A, SHIBATA T, et al. FEM-FDM coupled liquefaction analysis of a porous soil using an Elasto-plastic model[J]. Applied Scientific Research,1994, 52(3): 209－245.