三层结构导电聚合物驱动器动态特性及其建模研究*

刘怀民，王湘江

(南华大学机械工程学院，湖南衡阳421001)

0 引 言

导电聚合物是一类极具发展潜力的智能材料，基于导电聚合物聚吡咯(PPy)制备的导电聚合物驱动器具有许多优异的特性，如驱动电压低、生物适应性、重量轻、结构简单、抗电磁干扰、能在空气或液体介质的环境下工作等优点［1-3］，在生物机器人和生物医学设备中有巨大的应用前景［4-6］。微/纳米机构驱动应用也显示出极大的潜力［7-9］。然而，考虑到导电聚合物存在的动态非线性(包括零点漂移、迟滞现象等)［10-11］，为了使导电聚合物驱动器真正应用于实际系统，需对其位移的动态及静态特性有充分的认识和了解。

目前，针对导电聚合物驱动器动态特性研究和传统的控制方法对其实际应用和开发都存在一定的局限性。Madden［12］对双层导电聚合物驱动器建立了一个扩散-机械弹性变形的数学模型，Fang 等［13］将该模型扩展至三层EAP 驱动器，并基于简化的电化学模型开发了一种鲁棒自适应控制器。Yao 等［14］应用了PID控制方法提高驱动器的上升时间达500 倍，并在很大程度地减小了位置漂移现象。Shoa 等［15］则针对双层驱动器建立了一个等效传输线模型。其模型描述了驱动器尖端位移和电流的时间响应。上述研究中的模型主要依据驱动器内部结构所形成的双层并联电容器存在扩散阻抗，从而将这些模型限制在较低的频率范围内(＜4 Hz)。此外，Qi 等［16］应用比例控制器来提高聚苯胺驱动器的瞬态反应。Madden［17］将驱动器动态特性视为一阶系统，并设计了一个PID 控制器对PPy驱动器控制，以验证由PPy 驱动器和传感器组成的闭合回路。然而，Qi 等和Madden 设计的驱动器控制系统需要用到非接触式激光位移传感器位移作为反馈装置;目前激光位移传感器的尺寸远大于导电驱动器的尺寸，特别是将其应用于微/纳米机构驱动时，随着驱动器数量和自由度的增加，使用激光位移传感器变得更加不现实。

本研究通过建立三层结构导电聚合物驱动器等效电路模型进行实验分析。应用系统辨识的频率特性方法获得尺寸为12 mm ×2 mm 导电聚合物驱动器组成系统的高阶传递函数模型，并对模型动态位移输出结果与驱动器的实际位移输出进行比较分析。

1 驱动器及实验

1．1 驱动器结构

目前导电聚合物驱动器主要类型有双层弯曲型、多层弯曲型和直动型等，本研究所采用导电聚合物驱动器是一种三层结构的弯曲型驱动器。其结构可分为3 层:外面两层为聚吡咯(PPy)层(能发生体积膨胀与收缩)，中间层为多孔隙的聚偏二氟乙烯(PVDF，可储存离子液)，另外，PPy 层与PVDF 层之间还有极薄的镀金层(其厚度可以忽略，离子能迁移通过)。

驱动器结构示意图如图1 所示。

图1 导电聚合物驱动器结构示意图

1．2 驱动器运动机理

PPy 驱动器材料在PPy 层制备时掺杂有TFSI－，记为PPy/TFSI(二(三氟甲基磺酰)亚胺锂，其阴离子电荷分散程度高，阴离子半径在目前所见的电解质锂盐中最大，因此较易电离)。当驱动器上加载电压，正极的PPy/TFSI 发生氧化反应。负极PPy/TFSI 则发生还原反应。根据Chiarelli 研究结果，当使用的电解液存在较大阴离子时，聚合物氧化还原反应过程发生一次膨胀/收缩循环。依据Gandhi［18］建立的模型，正极PPy 氧化，负极PPy 还原，氧化PPy 层吸收阴离子产生扩张，还原PPy 层释放阴离子发生收缩。其化学变化过程如下式:

正极PPy 氧化膨胀:

负极PPy 还原收缩:

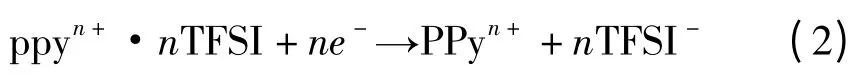
式中:ppy—处于中性状态;PPyn+—氧化态;PPyn+·nTFSI－—TFSI－离子与聚合物相结合;e－—电子。膨胀与收缩程度的差异造成驱动器的弯曲。同时，伴随离子扩散的溶剂分子也对PPy 层的体积变化有一定的影响，介于置换离子与聚合物共轭链的静电力也会引起PPy 层的膨胀和收缩。

1．3 动态特性测量系统

实验所用驱动器材料尺寸为12 mm ×2 mm，开始实验测试之前，已在浓度为0．5 mol/L 的Li+TFSI－/PC 离子液(PC 为碳酸丙烯酯试剂)中浸泡1 h(能确保驱动器能连续稳定工作数小时)，系统输入信号为正弦信号yi= sin(xt)，频率变化范围从10－3Hz～102Hz，数据采样周期设为0．002 s。传感器输出电压信号已标记为1 V/mm，记录数据之前驱动器已经正常运行10 min。激光位移传感器光斑焦点距夹钳端9 mm(有效长度)。驱动器自由末端贴有薄吸水纸片(重量可忽略不计，利于传感器信号接收)。

驱动器动态位移测量实验装置示意如图2 所示。具有高测量精度和响应速度的激光位移传感器(SENSOPART，FT 50 RLA-40-F-L4S)用于测量驱动器的动态位移变化。高速摄相机(FASTEC)用于图像采集和分析。激光位移传感器固定于XY 轴手动位移平台上(调节范围10 mm，精度0．5 μm)。Matlab/Simulink 产生驱动电压控制信号，经F20A 型函数信号发生器产生电压信号加载于夹钳(端头为铜片)两端，激光位移传感器测量驱动器位移变化并转化为电压信号，经PCI 数据采集卡(PCI-1710U)输入计算机，由Matlab/Smulink 记录测量数据。

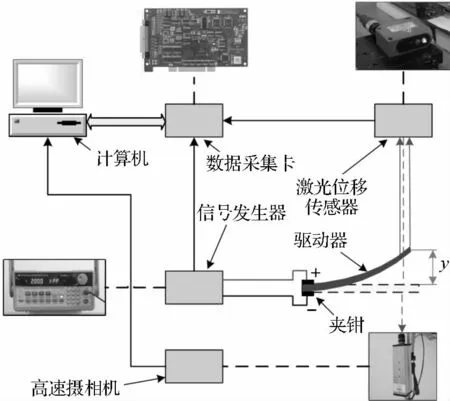
图2 动态位移测量系统示意图

2 动态特性建模与分析

2．1 等效电路模型及分析

驱动器两层聚吡咯层加载输入电压后，聚吡咯层和电解质之间产生电位差。在电势差的作用下，电解液中的阴离子向聚合物移动，其结果导致双层电荷聚集在聚合物/电解质界面(如同一个等效厚度为δ 的电容，需要考虑边界条件:离子只在PPy-PVDF 界面发生离子扩散，驱动器PPy 层-空气界面没有离子运动)，其等效电路如图3 所示。

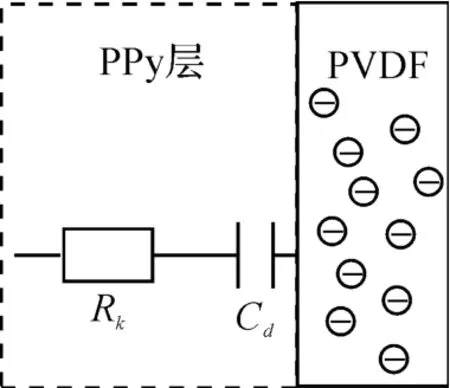
图3 导电聚合物层等效电路

此处，法拉第电流已忽略(聚吡咯发生氧化还原反应过程，电荷通过PPy 层-溶液界面形成的电流极小)。Rk由下式确定:

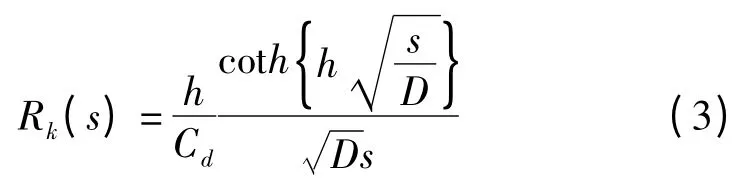
式中:D—扩散系数，h—导电聚合物层厚度。

笔者将Madden 提出的弹性金属扩散模型扩展至本研究所使用的三层结构导电聚合物驱动器，可将其简化为双层电容与扩散阻抗元件串联连接结构。本研究对驱动器中一个单元建立双层PPy/PVDF 层扩散阻抗Rk和电容Cd模型，等效电路图如图4 所示。三层结构导电聚合物驱动器等效电路模型(PPy/PVDF/PPy)如图5 所示。

此处，若PPy 层的单元电阻为Re，PVDF 层对应的单元电阻为Rp，假定驱动器在其长度上包含N 个单元阻抗，m 个总阻抗Rm(s)可由图5 计算得出:

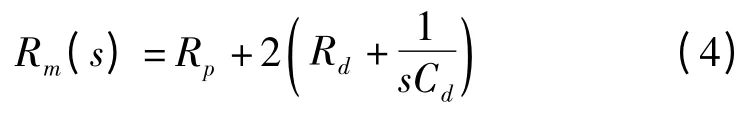
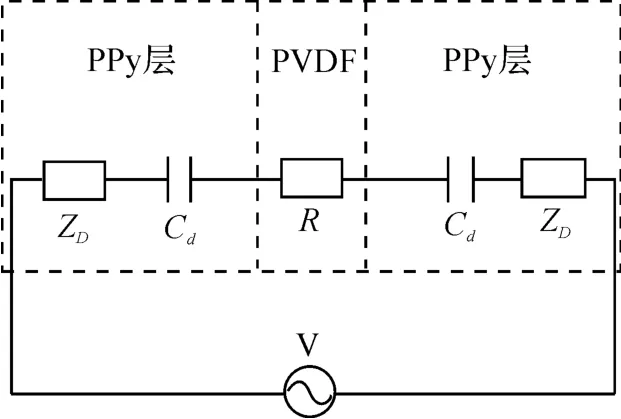
图4 三层结构导电聚合物单元等效电路图

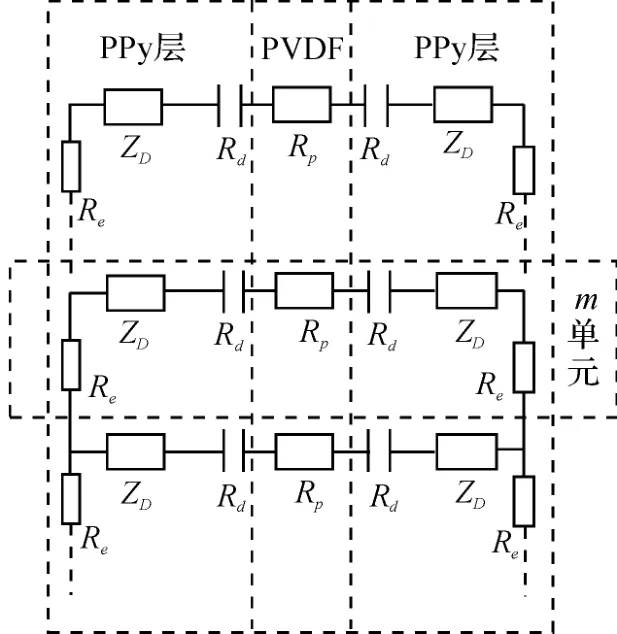
图5 三层结构导电聚合物驱动器等效电路图

根据前述文献中的三层结构导电聚合物驱动器总阻抗，由下式可得:

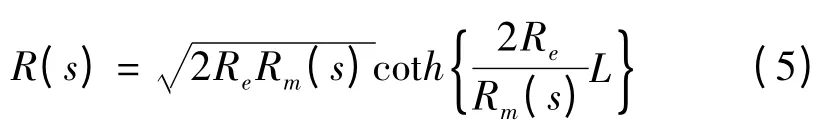
系统输入信号与输出信号幅值随正弦输入信号频率变化曲线如图6 所示。当正弦输入信号频率低于10－2Hz 时，输入信号与输出信号幅值(输出信号/位移=1 V/mm)具有最大值并保持不变，输出位移最大值2．763 7 mm，输入信号幅值为0．949 7 V。随着输入信号频率增大，输入信号与输出信号幅值逐渐减少，输入信号频率接近0．200 4 Hz 时，其幅值降至0．515 2 V，输出位移下降至1．152 4 mm． 此后，输入信号频率增大，其幅值基本保持不变而输出位移继续减小。当输入信号频率达到15．915 5 Hz 时，输出位移接近零。

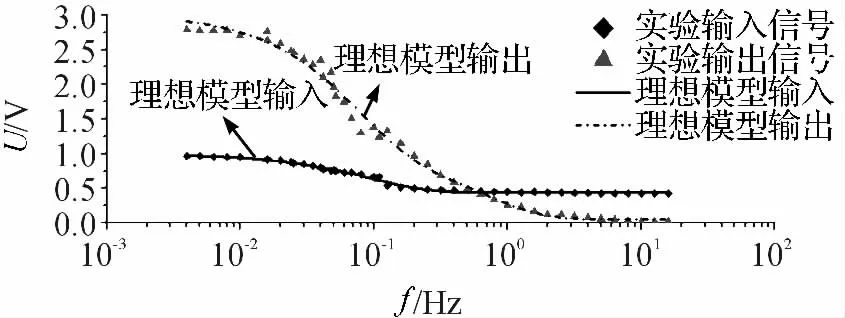
图6 输入信号与输出位移随频率变化图

图6 表明，驱动器位移及导电聚合物产生应力应变由低频段主导，同时也验证了文献［19］得出的结论:离子迁移速率限制导电聚合物产生的最大应变。驱动器的等效电路模型在低频段(＜10－2Hz)时，双层电容起对输入输出响应起主导作用，随着输入信号频率增大，双层电容对输出响应作用减小，阻抗元件作用加强;输入信号频率达到中高频时，双层电容和阻抗元件同时影响驱动器输入、输出响应。

2．2 频率特性参数模型

对于内部机理十分明确的系统，可利用相应的原理建立输入/输出与中间变量的关系获得描述系统的微分方程，并在零初始条件下进行拉普拉斯变换，就可以得到传递函数。但是，对内部机理不是十分明确或无法建立确定关系的系统，则需要通过建立系统的“黑箱”模型，并对这个“黑箱”用一定幅值、不同频率的正弦信号作输入yi=Aisin(ωt)，考察其稳态输出yd=Adsin(ωt+θ)。通过这些实验数据可绘制出对数幅频特性曲线，并采用渐近线逼近的方法获取传递函数参数从而得到传递函数G(s)。系统辨识的黑箱模型(输入信号(u(t)，U(s))，尖端位移输出(y(t)，Y(s))如图7 所示。

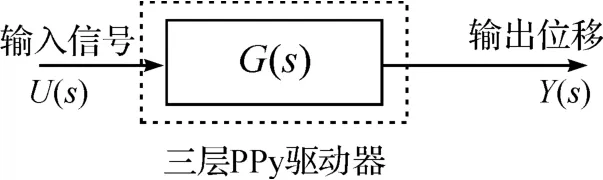
图7 系统辨识黑箱模型示意图

三层结构导电聚合物驱动器系统n 阶传递函数［20］:

本研究确定尺寸为12 mm ×2 mm 的驱动器组成系统阶次n 及各参数值，需对通过实验数据所得系统对数幅频特性曲线幅频特性上各环节的渐近线特性与相频特性上各环节的相位特点进行分析，对数幅频特性曲线的渐近线的斜率主要为0、±20(dB/dec)线、±40(dB/dec)线等。实验数据所得12 mm ×2 mm 驱动器系统对数幅频特性曲线如图8 所示。

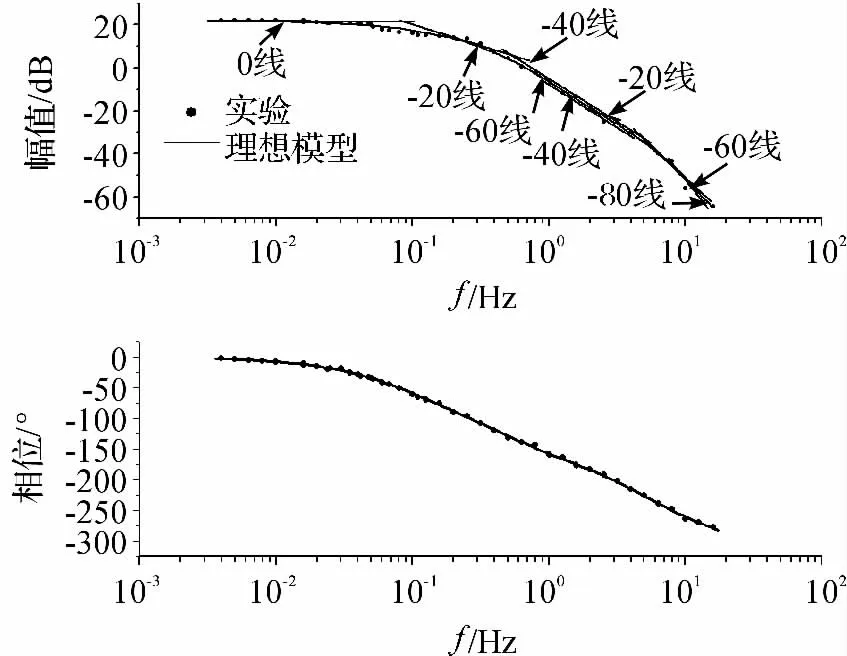
图8 12 mm×2 mm 驱动器系统对数幅频特性曲线

由图8 可知，该系统低频渐近线是一条20 lgK dB(K=12．534 1)的水平线，从低频向高频延伸，渐近线为:0 线、－20 线、－40 线、－60 线、－40 线、－20 线、－60 线、－80 线，该8 条渐近线共有8 个交点，对应的频率值分别为(单位:Hz):0．092 0、0．563 6、0．683 8、1．004、2．052 0、4．205 0、5．102 2、8．109 2。本研究利用图8 中曲线不同段渐近线斜率变化来确定系统的组成环节并对相位进行修正，从而获得该系统的不同阶次传递函数，12 mm×2 mm 驱动器系统不同阶次传递函数参数值及其与理想模型输出误差标准差如表1 所示。考虑到激光位移传感器对系统相位的影响，本研究进行2 ms延迟补偿。实验数据拟合理想动态模型与各阶次传递函数模型比较结果如图9 所示。

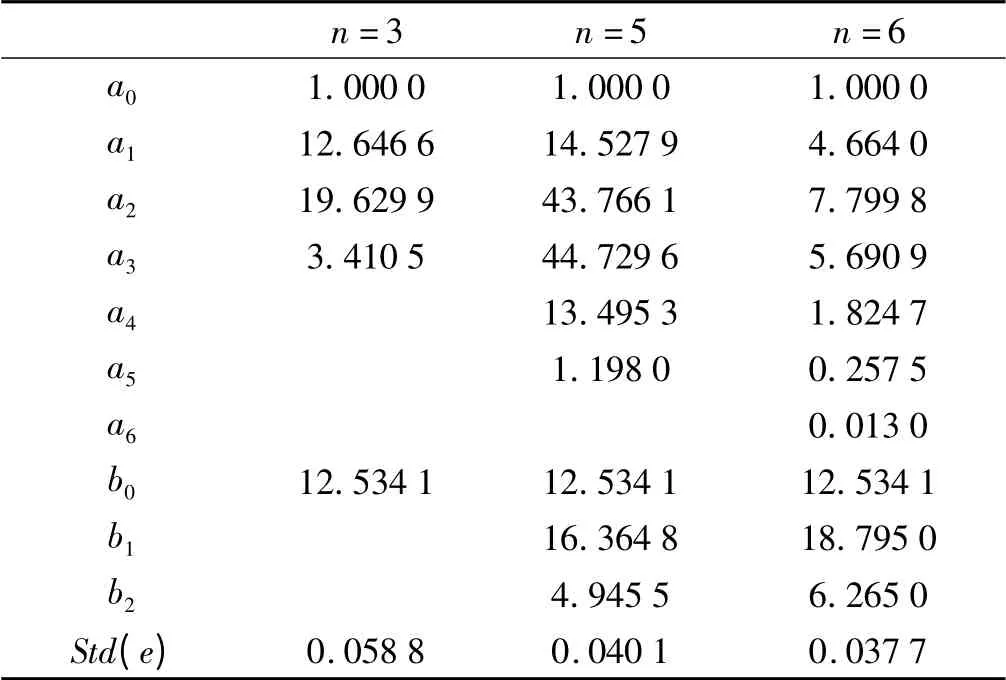
表1 传递函数参数值及误差标准差

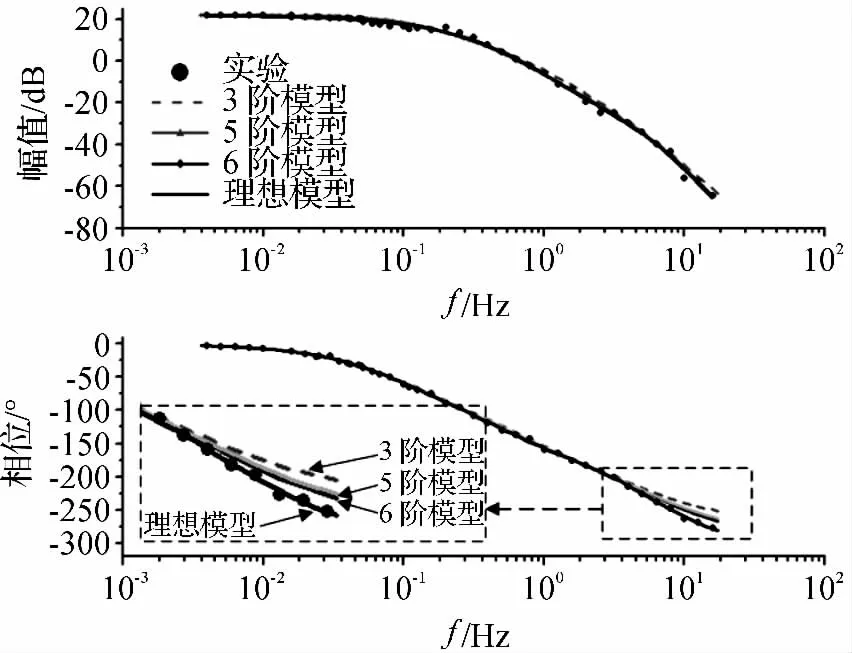
图9 不同阶次传递函数模型与理想动态模型比较

输入信号为y =sin(0．05t)各阶次模型输出与实际输出及其误差的比较如图10 所示。从图10 可知5、6 阶模型的输出与实际系统的输出之间的误差非常小，且两者的误差标准差相近，表明6 阶模型有效地预测驱动器动态位移响应。此时，驱动器动态非线性因素(零点漂移、迟滞现象等)对误差有较大影响。

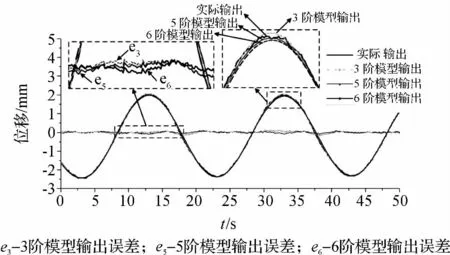
图10 各阶次模型输出与实际输出及其误差比较

3 结束语

本研究通过建立动态特性测量系统对三层结构导电聚合物驱动器的动态特性问题进行了研究，得到以下结论:

(1)基于三层结构导电聚合物驱动器PPy 层氧化还原反应过程引起膨胀收缩机理所建立的等效电路模型能够有效地描述驱动器的动态输入/输出特性，驱动器位移及导电聚合物产生应力应变由低频段主导。

(2)应用系统辨识的频率特性方法获得三层结构导电聚合物驱动器组成系统高阶传递函数模型能精确有效地预测驱动器动态位移响应，6 阶模型输出与实验结果误差非常小，说明了模型的有效性。并且该模型可用于较大频率范围内驱动器对任意输入信号的输出位移响应。为了进一步提高模型精度，后继的研究工作应考虑驱动器的动态非线性因素。

［1］BAUGHMAN R H． Conducting polymer artificial muscles［J］． Synthetic Metals，1996，78(3):339-353．

［2］SMELA E． Conjugated polymer devices for biomedical applications［J］． Advanced Materials，2003，15(3):481-494．

［3］ALICI G，HUYNH N N． Performance quantification of conducting polymer actuators for real applications:a microgripping system［J］． IEEE/ASME Transactions on Mechatronics，2007，12(1):1-12．

［4］MAZZOLDI A， DEROSSI D． Conductive-polymer-based Structures for a Steerable Catheter［C］． SPIE 2000 Smart Structures and Materials:EAPAD． Newport Beach:［s．n．］，2000:273-280．

［5］李新贵，张瑞锐．导电聚合物人工肌肉［J］．材料科学与工程学报．2004，22(1):128-131．

［6］MANTO M，TOPPING M，SOEDE J，et al． Dynamically responsive intervention for tremor suppression［J］． IEEE transactions on bio-medical engineering，2003，22(3):120-132．

［7］SMELA E，INGANAS O，LUNDSTROM I． Controlled folding of microsize structures［J］． Science，1995，268(5218):1735-1738．

［8］JAGER W H，INGANAS O，LUNSTROM I． Microrobots for micrometer-size objects in aqueous media:potential tools for single cell manipulation［J］Science，2000，288(5415):2335-2338．

［9］ZHOU J W，CHAN H Y，LAI W C，et al． Polymer MEMS actuators for underwater micromanipulation［J］． IEEE/ASME Transactions on Mechatronics，2004，9(2):334-342．

［10］CARPI F，DEROSSI D． Electroactive polymer-based devices for e-textiles in biomedicine［J］． IEEE Trans． Inf．Technol． Biomed，2005，9(3):295-318．

［11］ALICI G，MUI G，COOK C． Bending modeling and its experimental verification for conducting polymer actuators dedicated to manipulation applications［J］． Sens． Actuators A，Phys，2006，126(2):396-404

［12］MADDEN J D． Conducting Polymer Actuators［D］． Cambridge:Massachusetts Institute of Technology，2000．

［13］YANG F． Robust adaptive control of conjugated polymer Actuators［J］． Control Systems Technology，2008，16(4):600-612．

［14］YAO Q，ALICI G，SPINKS G M． Feedback control of trilayer polymer actuators to improve their positioning ability and speed of response［J］Sens． Actuators A，2008，144(1):176-184．

［15］SHOA T． A dynamic electromechanical model for electrochemically driven conducting polymer actuators ［J］．Mechatronics，2011，16(1):42-49．

［16］QI B，LU W，MATTES B R． Control System for Conducting Polymer Actuators in Smart Structures and Materials［C］//SPIE2000 Smart Structures and Materids:EAPAD SanPiego:［s．n．］，2002:359-366．

［17］MADDEN P G A． Development and modeling of conducting polymer atuators and the fabrication of a conducting polymer based feedback loop［D］． Cambridge:Massachusetts Inst．Technol，2003．

［18］GANDHI，MURRAY P，WALLACE G，et al． Mechanism of electromechanical actuation in polypyrrole［J］． Synthetic Metal，1995，73(3):247-256．

［19］MADDEN P，MADDEN J，ANQUETIL P，et al． The relation of conducting polymer actuator material properties to performance［J］． IEEE Journal of Oceanic Engineering，2004，29(3):696-705．

［20］OGATA K． Modern control Engineering［M］． Upper Saddle River:Prentice Hall，2002．