基于PFC3D的研磨片研磨过程离散元仿真*

应振根，冯凯萍，倪成员

(衢州学院机械工程学院，浙江衢州324000)

0 引 言

目前，跳线光纤头端面主要采用研磨片加工。由于涂覆在薄膜上的磨粒层为10 μm～50 μm，无法进行修整，研磨片存在表面磨粒钝化速度快、寿命短的问题。因此，对磨粒层中磨粒的结合力控制是获得高质量研磨片的关键。合适的结合剂强度下，当作用一定的研磨压力，表层结合剂无法对周围磨粒产生足够的把持力，使钝化磨粒脱落，新的磨粒露出，达到修锐研磨片、延长研磨片寿命的目的。研磨过程是一个高度动态性、非线性的过程，需要经验或半经验的数据来优化过程中的各个参数，以达到所需的加工结果［1］。

目前，人们已开始利用计算图形技术来模拟磨具研磨过程。沈阳理工大学的康杰等人［2］对单颗粒脆性材料冲击破碎进行了三维数值模拟。西安建筑科技大学的廉小庆等人［3］运用ANSYS/LS-DYNA 的三维显式动力研究了磨料形状和粒径对材料冲蚀磨损性能的影响。合肥工业大学的赵永春等人［4］对运动离散元对摩擦过程表面形貌动态变化进行了模拟研究。湘潭大学的姜胜强等人［5］对碳化硅陶瓷预应力加工进行了离散元模拟研究。由于磨具中主要包含磨粒，具有离散特性，而非连续特性，离散单元法是一种较理想的数值方法。

本研究主要根据研磨片的参数特性，建立离散元模型，对研磨过程进行模拟，观测磨粒脱落情况，分析不同结合强度和不同砂结比条件下，光纤头和研磨片的相互作用情况。

1 散元模型理论

离散元素法的基本原理是，将研究对象划分为一个个相互独立的单元，根据单元之间的相互作用和牛顿运动定理计算单元的受力及位移，并更新所有单元的位置［6］。

基本假设:

(1)颗粒单元为刚性球体;

(2)接触发生在很小的范围内，即点接触，接触处有特殊的连接强度;

(3)接触特性为柔性接触，接触处允许有一定的“重叠”量，大小与接触力有关，且远小于颗粒直径;

(4)一个时间步长内，除了直接接触的单元，其它单元的扰动不能传播过来［7］。

离散颗粒模型是将颗粒与颗粒、颗粒与边界的接触采用振动的运动方程进行模拟，离散元接触模型表示振动模型如图1 所示。

图1 离散元接触模型表示振动模型

将颗粒接触过程的振动运动进行法向和切向分解，颗粒接触过程的法向振动运动方程为［8］:

颗粒接触过程的切向振动运动表现为切向滑动和颗粒的滚动:

式中:m1，2—颗粒i，j 的等效质量;I1，2—颗粒的等效转动惯量;s—旋转半径;un，us—颗粒的法向和切向相对位移;θ—颗粒的自身旋转角度;Fn，Fs—颗粒所受外力的法向分量和切向分量;M—颗粒所受外力矩;Kn，Ks—接触模型中的法向及切向弹性系数;cn，cs—接触模型中的法向及切向阻尼系数。

颗粒的切向滑动与颗粒的滚动同时受颗粒间摩擦力影响，由滑动模型可以建立颗粒的切向滑动与滚动滑动的极限判断条件:

2 离散元建模

2．1 研磨片原型

三维离散颗粒单元模拟研磨片显微图如图2 所示，研磨片主要包括薄膜基材、磨料涂覆层，磨料涂覆层主要由磨料和结合剂组成。磨料平均粒径为3 μm，研磨片中结合剂包括控制涂层粘结性质的主粘结剂、控制涂层硬度的辅粘结剂、提高磨粒分散性的分散剂、控制涂层带电的防止带电剂等。

图2 研磨片截面显微图

2．2 研磨模型的建立

在研磨片和光纤头端面接触和摩擦过程中，两表面的实际接触只发生在部分微凸体上，为简化起见，本研究把摩擦表面简化为一个光滑表面和一个理想粗糙表面［9］，研磨模型如图3 所示。

图3 研磨模型

光滑表面为研磨片磨粒涂层，考虑到涂层中4 μm以下的磨粒与粘结剂的力学特征比较稳定，兼顾到离散元计算效率，本研究中的研磨片离散元模型认为是由0．5 μm以上的磨粒和粘结剂、空隙所组成，磨粒单元半径2 μm～4 μm，结合剂单元半径0． 5 μm～1．5 μm。本研究把上述颗粒按照一定的级配，投放于长、宽和高为10 mm、10 mm和5 mm 的空间内，研磨片磨粒单元和结合剂单元的砂结比为1∶6。

理想粗糙表面是光纤头端面粗糙峰层，即表面有3 个梯形凸起的粗糙峰，用来模拟工件的粗糙表面，单元半径1 μm，总长度为5 mm，在一定的压力P 作用下，以一定的速度v 相对运动，粗糙表面与光滑平面接触。上表面与下表面相对运动所产生的摩擦力为f。模拟计算中两表面的相对位移为20 mm，相对速度设定为10 m/s～30 m/s，设定压力P 为15 MPa～35 MPa。在模拟过程中，每个时步长为4．411 ×10－11s。

2．3 宏观和微观参数表征

使用离散单元法进行模拟分析时，研究者必须找出样本的宏观行为与微观颗粒的行为之间的关系。宏观力学参数不仅与磨粒的强度、大小、形状和分布有关，还受磨粒和胶结物的变形和强度特性的影响，这时，很难选择合适的属性参数使得模型的综合行为与实际材料完全匹配。研究发现，通过离散元模拟双轴试验，能够有效地确定离散元模拟中基本宏观参数和细观参数之间的尺度定律［10］。通过双轴试验反复调整颗粒输入细观参数，直至结果与试验用工件材料的物理力学性质接近。通过计算最后得出研磨片内摩擦角为25． 3°，凝聚力为1． 52 MPa，杨氏模量为31．5 MPa，泊松比为0．36，光纤头插芯的材料为陶瓷材料，通过查询文献［11］可得陶瓷离散元参数，此时的颗粒细观参数如表1 所示。

本研究通过对材料的模拟，考虑表面接触时表面形貌的变化和磨损情况。颗粒在受到大于其粘结强度的外力时，颗粒间的粘结会破坏，颗粒会分离，常用来模拟颗粒的脱落行为。在PFC3D 中单元间的受力通过单元间的力链来表示，拉伸力和加压力可用特定的线条表示，线条越粗，表示单元间的受力越大，应力越大。

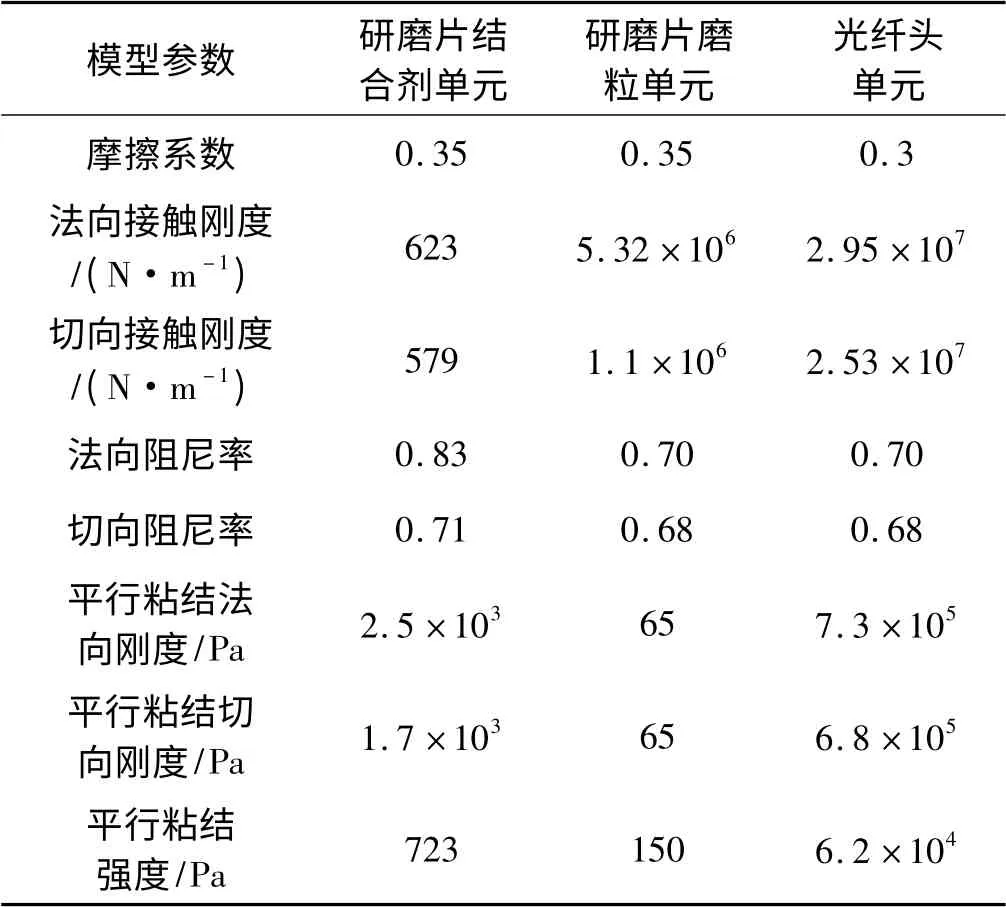
表1 离散元模型参数

3 结果分析

3．1 研磨过程仿真

研磨过程仿真如图4 所示，图4 中的粗线条代表单元之间的力链，用来标识表面应力的大小，应力主要分布在与上表面接触点的下方。在光纤头插芯端面平移0．01 ms 后，表面粗糙峰开始接触到研磨片表面，粗糙峰承受研磨片表面磨粒的作用力，内力变大，单元之间的黏着力效应还存在，粘结作用没有遭受破坏，在接触点处的单元间的接触力呈现散射样式逐步减弱，表面变形为弹性变形，部分单元有很小的压缩变形，如图4(a)所示。

在光纤头插芯端面平移0．25 ms 后，第2 个表面粗糙峰接触到研磨片表面，第一个粗糙峰最上层单元出现偏斜，与最上层单元接触处的竖向黏结效应丧失，已被压溃，出现比其他粗糙峰更严重的颗粒单元脱落现象，如图4(b)所示。这是因为当应力超出材料的弹性极限，粗糙峰形貌开始出现变化，为塑性变形状态，单元的偏移和脱落方向与表面相对运动方向一致，在压力和相对移动引起的黏着效应下，粗糙峰的变形量逐步增大。

在光纤头插芯端面平移0．5 ms 后，第3 个粗糙峰接触到研磨片表面，此时，工件端面内力巨大，粗糙峰下均出现裂纹，第一个粗糙峰下的裂纹达到最大情况，但相比图4(b)没有出现较大的形状变形，说明粗糙峰上的应力在逐步地增大，为应力积聚期，如图4(c)所示。

在光纤头插芯端面平移0．75 ms，前一个粗糙峰离开了研磨片表面，此时，粗糙峰已被磨平，表面变得光滑，如图4(d)所示。这是因为剪切应力和拉伸应力达到材料的强度极限，单元间的黏着力效应消失，单元间就会出现断裂现象，或者导致某些单元的脱落。

在光纤头插芯端面平移1 ms 后，工件端面与研磨片表面完全分离，基体整个过程中出现的裂纹消失，粗糙峰去除，表面光滑，达到了机械研磨材料去除的效果，如图4(e)所示。而此时，研磨片内力在最后接触的地方内力最大，沿着工件端面进来的方向分散开来，这是因为上、下表面间的单元磨粒体存在接触黏结作用，而下表面其相邻的单元在黏着力的作用下会阻碍上层单元运动，这样上下单元间就会存在X 向剪切应力，而平行相邻的单元存在X 向拉伸应力，导致了内力的增大。

图4 研磨过程表面形貌变化图

根据图4 的研磨过程表面形貌变化图，笔者记录下未脱落颗粒563 和邻近的脱落颗粒564 的不平衡力随时间步变化图如图5 所示，接触初期，不平衡力急剧上升，这是由于在由弹性变形到塑性变形转变的瞬间，不平衡力会出现一个峰值，随后会有所回落。而后未脱落单元的不平衡力呈现周期性波动，这是由于粗糙峰在压力作用下以一定的速度越过研磨片上的颗粒单元时，上层颗粒单元会周期性地正压和反压在下层颗粒单元上，不平衡力会出现周期性浮动，如图5(a)所示，而脱落颗粒单元则出现不平衡力急剧下降的情况，最终不平衡力为零，如图5(b)所示。

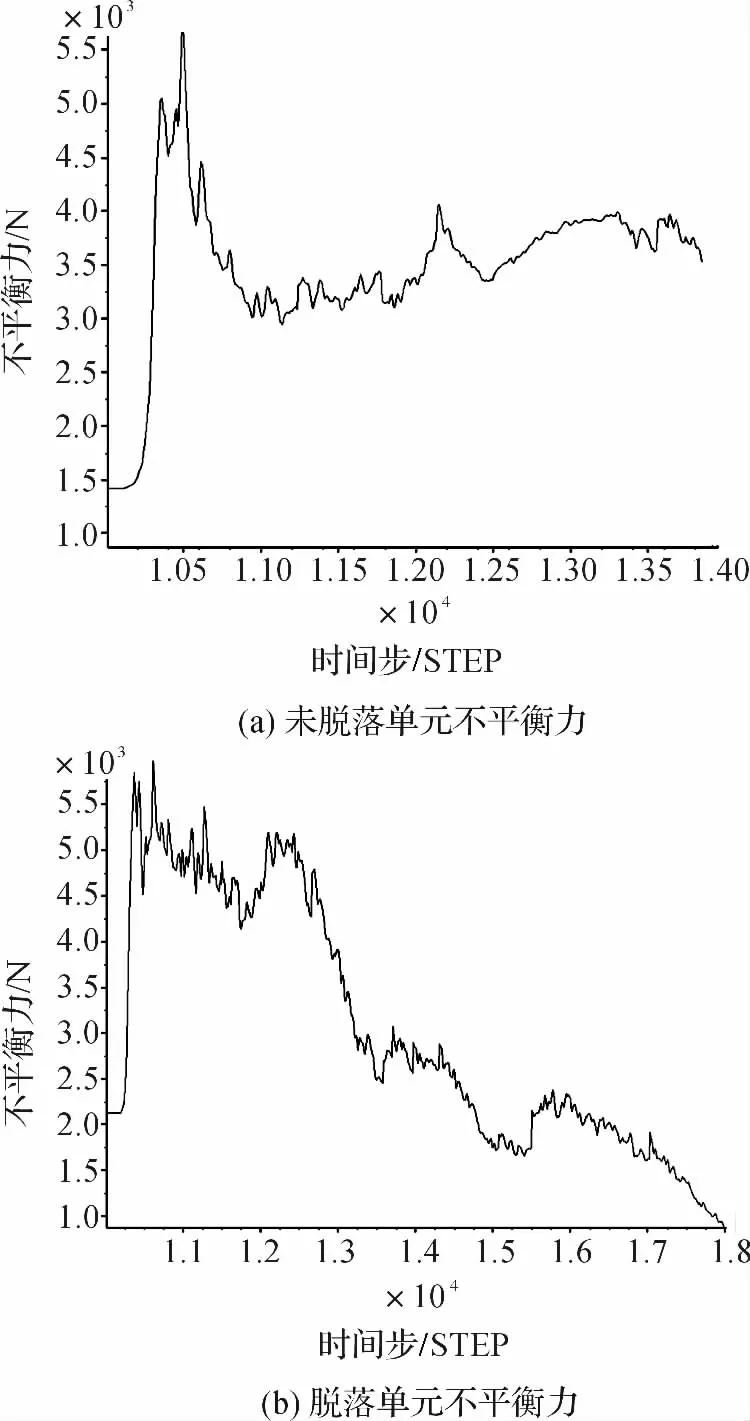
图5 单元不平衡力随时间步变化图

从整个仿真过程中可以看出，表面形貌的变化主要受到2 个因素的影响:切向黏着力和法向压力，切向黏着力是由两接触表面间相对速度引起的，法向压力主要来源于施加的研磨载荷。在压力的作用下粗糙峰与颗粒单元挤压，最高处容易出现塑性变形，这是由于法向应力超出材料应力极限的结果;在速度作用下，下表面与上表面接触点处存在黏着效应，颗粒单元在黏着效应的作用下切向应力超出剪切应力极限，单元脱落。

3．2 结合强度对研磨过程的影响

本研究通过改变结合剂的粘结强度和刚度，研究结合强度对研磨过程的影响，将研磨片结合剂单元的平行粘结法向刚度减小到1．25 ×103Pa，平行粘结切向刚度减小到0．85×103Pa，平行粘结强度减小到360 Pa，不同粘结强度研磨片形貌变化图如图6 所示，从图6(a)中可以看出，研磨过程中，光纤头端面的粗糙峰不能完全去除，而研磨片表面的磨粒和结合剂则出现溃散的现象，这是因为在研磨过程中结合剂不能有效把持住磨粒单元，磨粒单元与粗糙峰接触过程中，磨粒单元的结合强度先于粗糙峰单元的结合强度失效，磨粒大量脱落，研磨片的磨粒涂覆层消耗极大，这不符合研磨片的寿命要求。

图6(b)中提高了结合剂的粘结强度，将研磨片结合剂单元的平行粘结法向刚度增大到5 ×103Pa，平行粘结切向刚度增大到3．4 ×103Pa，平行粘结强度增大到1 446 Pa，研磨过程中，粗糙峰的去除很快，在0．5 ms内已完全去除，而研磨片表面则没有发生很大的变化，有微量的结合剂和磨粒单元脱落出来，这是因为结合剂的粘结强度高，研磨片刚度大，在相互接触摩擦过程中，粗糙峰结合强度首先失效，发生断裂，该条件下，虽对粗糙峰的去除效率高，但在实际研磨过程中，磨粒容易对工件表面产生划痕，同时磨粒长时间磨削，无法脱落，会导致磨粒钝化，材料去除效率下降。

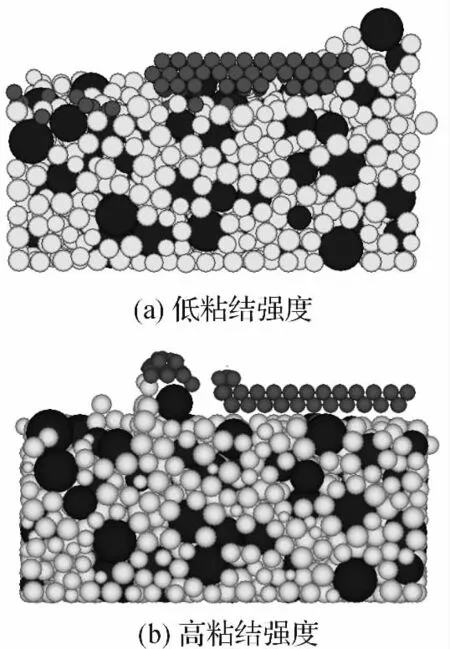
图6 不同粘结强度研磨片形貌变化图

3．3 砂结比对研磨过程的影响

本研究通过改变磨粒单元和结合剂单元的砂结比，研究砂结比对研磨过程的影响。图4 中研磨片的砂结比为1∶6，工件表面粗糙峰被去除，研磨片表层磨损磨粒脱落，达到了理性的材料去除效果。不同砂结比研磨片形貌变化图如图7 所示，将研磨片涂层中的砂结比增加到1∶3 的形貌变化图如图7(a)所示，由于砂结比的提升，结合剂含量相对下降，磨粒不能有效被结合剂把持住，磨粒脱落量大，易在工件表面进行滚动摩擦，不符合研磨片要求。

将研磨片涂层中的砂结比下降到1∶9 的形貌变化图如图7(b)所示，由于砂结比的下降，结合剂含量相对增加，但结合剂接触刚度低，无法对粗糙峰表面的单元进行有效去除，而研磨片中的磨粒由于被结合剂牢牢黏住，无法脱落。研磨片应用中，在保证结合强度的条件下，提高砂结比有利于提高研磨效率。

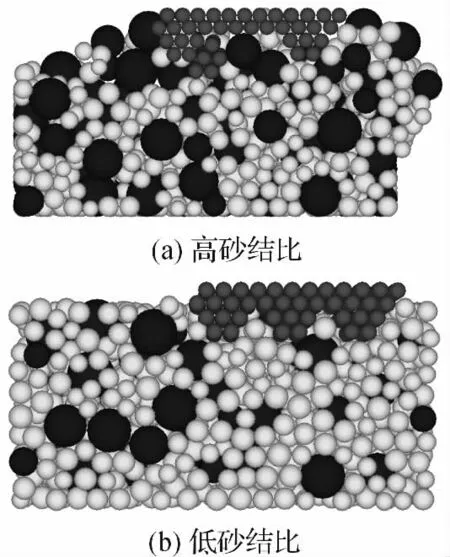
图7 不同砂结比研磨片形貌变化图

4 结束语

通过基于离散元法的研磨片和光纤头端面研磨过程模拟，本研究得出以下结论:

(1)磨粒单元脱落过程是一个弹性变形-塑性变形-结合键断裂-脱落的过程，磨粒受力反应在不平衡力上，其在接触点处的不平衡力呈现散射样式逐步减弱，不平衡力峰值为5．9 ×103N，脱落磨粒不平衡力趋向于零，未脱落磨粒在3．5 ×103N 上下波动。

(2)通过研究结合剂结合强度对研磨过程影响表明，结合剂的粘结强度高，磨粒无法脱落进行自修整;结合剂强度低，磨料涂覆层易发生流动，磨粒无法进行滑动摩擦，去除材料，同时磨粒涂覆层损耗速度快;当磨粒涂覆层平行粘结强度为723 Pa 时，研磨效果好。

(3)通过研究砂结比对研磨过程影响表明，砂结比达到1∶3 时，结合剂的减少导致磨粒涂覆层松散，无法对光纤头端面进行有效研磨;砂结比达到1∶9 时，作用磨粒少，无法破坏粗糙峰上单元的连接键，粗糙峰无法去除;砂结比达到1∶6 时，研磨效果最好。

［1］XV Jin，LUO Jian-bin，LU Xin-chun，et al． progress in material removal mechanisms of surface polishing with ultra precision［J］． Chinese Sci． Bulletin，2004，49(16):1687-1693．

［2］康 杰．单颗粒脆性材料冲击破碎三维数值模拟［D］．沈阳:沈阳理工大学装备工程学院，2010．

［3］廉晓庆，蒋明学，白顶有． 基于ANSYS/LS-DYNA 的磨料冲击行为分析［J］．硅酸盐通报，2010，29(2):409-412．

［4］赵永春． 摩擦过程表面形貌动态变化模拟研究［D］． 合肥:合肥工业大学机械工程学院，2009．

［5］姜胜强，谭援强，聂时君，等．碳化硅陶瓷预应力加工的离散元模拟与实验研究［J］．无机材料学报，2010，25(12):1286-1289．

［6］刘凯欣，高凌天． 离散元法研究的评述［J］． 力学进展，2003，33(4):483-490．

［7］胡 励．机械产品设计中的颗粒离散元仿真技术及实现［D］．武汉:武汉大学动力与机械学院，2013．

［8］范亮平．集料均匀性对沥青混合料力学性能影响的离散元模拟［D］．杭州:浙江大学建筑工程学院，2014．

［9］刘小君，魏庆森，张 彦，等．基于离散元法的粗糙表面摩擦过程数值模拟［J］． 合肥工业大学学报，2011，34(1):23-27．

［10］邹 猛，李建桥，贾阳，等．月壤静力学特性的离散元模拟［J］．吉林大学学报，2008，38(2):383-387．

［11］TAN Y Q，YANG D M，SHENG Y． Discrete element method (DEM)modeling of fracture and damage in the machining process of polycrystalline SiC［C］//The European Ceramic Society 2008． Portugal:［s． n．］，2008:236-240．