超声检测并联机器人位姿分析研究*

沈 伟 ，吴瑞明 ，刘云峰

(1．浙江工业大学机械工程学院，浙江杭州310014;2．浙江科技学院机械学院，浙江杭州310023)

0 引 言

超声检测机器人是集数控、超声信号处理及超声成像等多学科技术于一体的超声检测系统。在复杂形状工件的超声检测中，如何做到实时调节和控制探头姿态和位置，使探头在检测过程中保证准确发射/接受声波信号，是检测工作中要解决的一个很重要的问题［1］。

在超声检测运动控制研究中，浙江大学王艳颖，周晓军等［2-4］将超声检测技术与串联机器人技术结合应用。但串联机器人的末端执行器的误差是各个关节误差的累积和放大，因而误差大而精度低，文献［5-6］通过误差补偿提高超声检测的精度。而并联机器人却没有那样的累积和放大关系，误差小而精度高;在位姿求解上，并联机器人的反解非常容易，而串联机器人反解复杂且多值，从这一点来看，在工作空间内进行并联机器人位姿控制是比较容易的。

基于并联机器人以上的优势，以超声检测探头位姿精确控制为目标，本研究提出将超声波探头(换能器)安装在6-UPS 钢带并联机器人上，通过对该超声检测并联机器人进行运动学分析，可为实现自由曲面的连续超声波扫描检测提供位姿精确控制的算法。

1 超声检测原理

1．1 超声背散射评价晶粒度原理

超声散射波虽然会影响超声检测过程中的超声成像，如以杂波的形式出现，但散射波中也携带着有关材料微观结构非常重要的信息，如果进行适当地建模可以用来评价材料的晶粒度［7］。目前国内还不太有对这方面的研究，国外已经提出了几种模型和方法来研究超声漫散射与材料晶粒度之间的联系。美国内布拉斯加大学林肯分校Tuner 教授［8］提出了以深度为函数的SSR 模型，其检测基本原理如图1 所示。

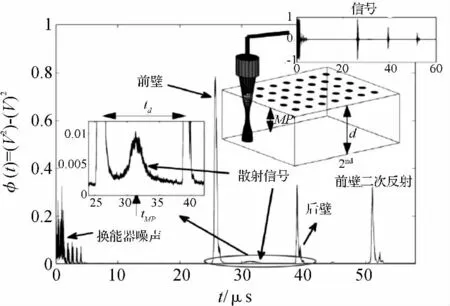
图1 超声背散射原理

通过Φ(t)与微观结构量建立关系，SSR 的最后一个表达式由下式给出:

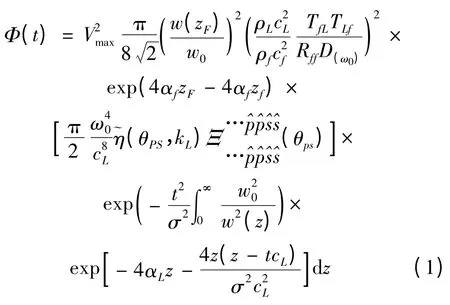
式中:ρL，cL—样品的密度和纵波在样品中的速度;ρf，cf—液体的密度和波在液体中的速度;D(ω0)—ω0的衍射校正，并作为输入波的中心频率，w0—换能器孔径的半径;w(zF)—高斯光束的宽度，zF—校准反射振幅Vmax期间测得的从换能器表面到该反射平面之间的水通道距离;αf—流体的衰减系数;zf—后向散射实验中换能器的表面到样品之间的水通道距离。

式(1)表示的是流-固界面超声散射理论的实验结果。这个SSR(单次散射)模型可分为3 个主要部分。式(1)的前两行表示的是与换能器参数，样品流体参数和整体性质相关的参数。固、液之间的透射系数分别由以下两式给出:

TLf=TfL(2ρfcf)/(ρLcL)，TfL=2ρfcf/(ρLcL+ρfcf)。

Rff=(ρLcL－ρfcf)/(ρLcL+ρfcf)定义的是反射系数。

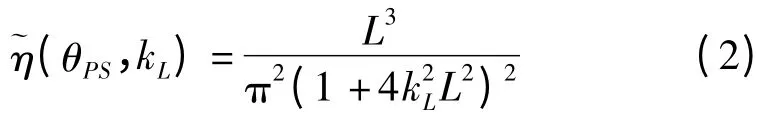
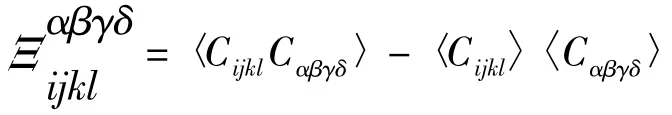
式中:〈Cijkl〉—二阶弹性系数张量，有81 个分量(尖括号〈〉表示集合平均值);矢量p，s—入射和散射波的传播方向。例如在一个立方晶体中:

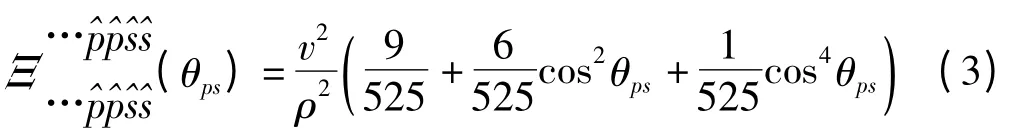
式中:v—单晶各向异性因子，v=c11－c12－2c44。

式(1)剩余项定义的是当超声波穿透试件时平均波束的行为。其中:αL—固体的衰减系数，σ—输入波的时间宽度。高斯波束宽度可以写成:

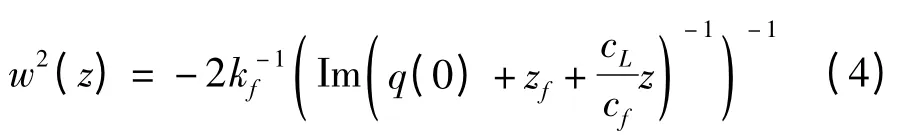
式中:kf—在液体中的波数，kf=ω0/cf，q(0)=(－F－1+，F—换能器的焦距。

而式(1)中等号的左边:

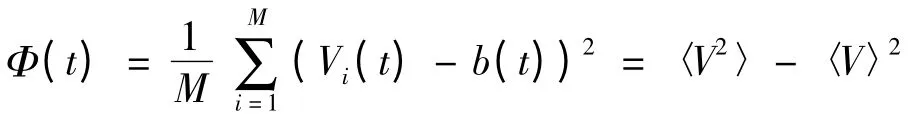
通过求解各扫查点信号的平方值与各扫查点信号平均值的平方的差值(即Φ(t))，建立Φ(t)与晶粒度之间的函数关系是实现超声检测评价试件晶粒度的一种方法。Φ(t)的实验值与理论值偏差对比如图2所示。Φ(t)值是一个数值较小的值，在实验研究过程中，很容易因探头位姿不到位产生的误差而引起Φ(t)的实验值与理论值产生较大偏差如图2(b)所示。所以要控制超声检测过程中误差在合理范围内，提高检测过程中控制的精确度尤其是对探头位姿控制的精度对检测结果具有积极影响。

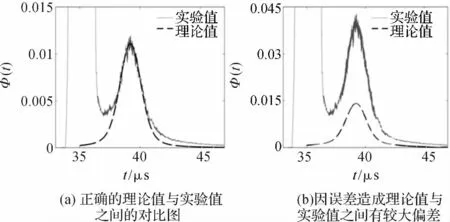
图2 Φ(t)的实验值与理论值偏差对比

因并联机器人相比串联机器人具有更小的末端误差，以及位姿控制计算更容易等优点，本研究尝试将超声检测技术与并联机器人技术结合应用，为自动化超声评估材料晶粒度提供一种平台思路。而位姿分析是超声检测并联机器人其他运动分析的前提和准备，故本研究从位姿分析出发，为计算机控制超声检测并联机器人的提供一种算法。

1．2 超声检测并联机器人

2 超声机器人位姿分析

已知超声探头的位置和姿态，求解输入件的位置称为机构的反解。在并联机器人的运动过程中，不论是钢带，还是动平台，都将产生复杂的运动。但如果把这些物体看成是刚体，那么就可以用描述一个刚体在空间的位置和姿态的方法来描述它们在空间的位姿［10-11］。本研究在笛卡尔坐标系内进行描述，在动平台和静平台上分别建立动静坐标，用xb，yb，zb，和αb，βb，γb来描述动平台的位姿，再通过动静坐标系之间的坐标转换，得到动平台上三点在静坐标系下的坐标。由两点坐标求得两点间的距离，即钢带长度。

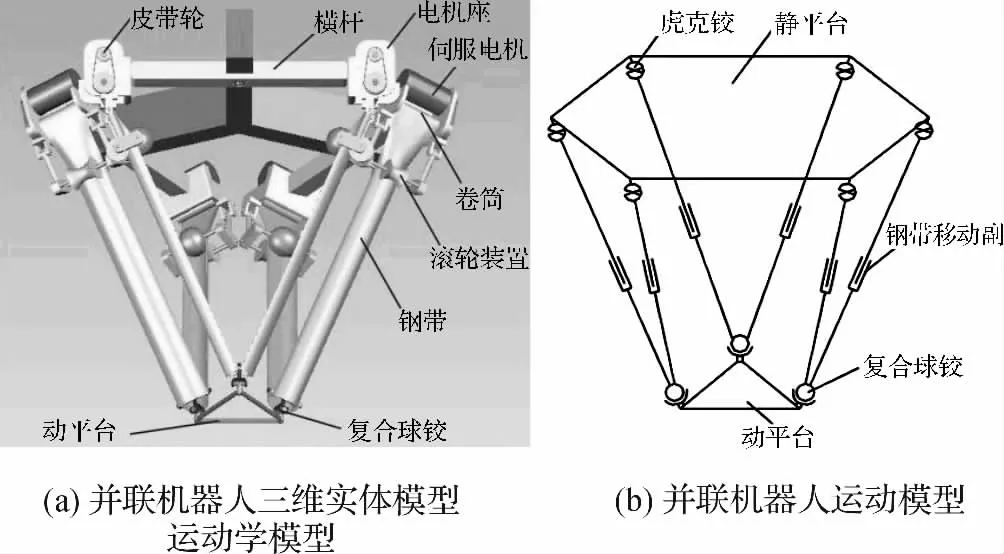
图3 并联机器人三维模型和运动模型

2．1 超声检测机器人数学模型

本研究在机构的上平台建立一个固定坐标系OXYZ，原点O 位于上平台A1A2A3A4A5A6六边形的几何中心，O-XYZ 的Z 轴垂直于上平台平面向上，X 和Y 轴如图4(a)所示。在机构的下平台建立一个动坐标系O'-X'Y'Z'，其原点O'位于下平台三角形B1B2B3的几何中心，其Z 轴在初始状态时垂直于下平台平面向上，动坐标系的X 轴和Y 轴分别平行于静坐标系的X轴和Y 轴。机构坐标俯视图如图4(b)所示，设A1A2A3A4A5A6六边形外接圆半径为R，等边三角形B1B2B3外接圆半径为r。设(xb，yb，zb)是下平台O'点相对定坐标系O-XYZ 的坐标。

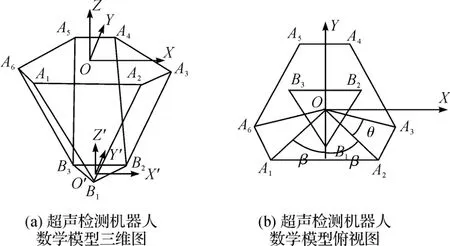
图4 超声检测机器人数学模型

在图4(b)中，定平台基座六点A1，A2，A3，A4，A5和A6均在以半径为R 的圆上，A1和A2，A3和A6，A4和A5分别关于Y 轴对称。其中A1和A2的夹角，A3和A4的夹角，A5和A6夹角均为β(0° ＜β ＜120°)。则在静坐标系下A1，A2，A3，A4，A5和A6的坐标为:

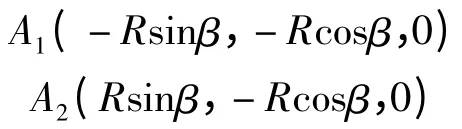
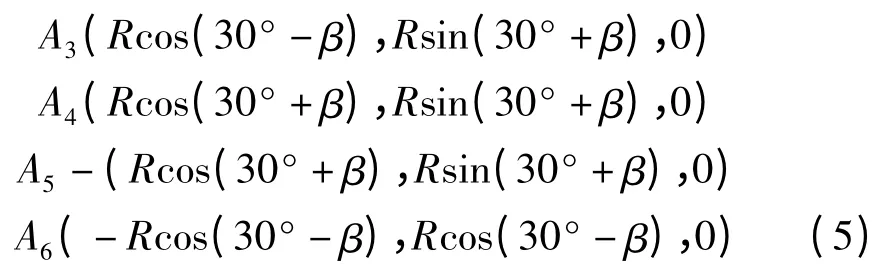
B1，B2，B3在动坐标系O'-X'Y'Z'下坐标分别为:

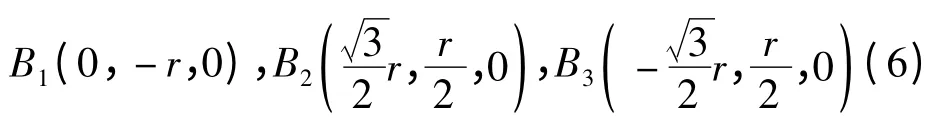
2．2 坐标转换

在动坐标系中的任一矢量b'可以通过变换矩阵变换为固定坐标系中的b，即:

其中:bo=［xbybzb］T，bo—上平台选定的参考点，即动坐标原点O'在固定坐标系中的坐标。

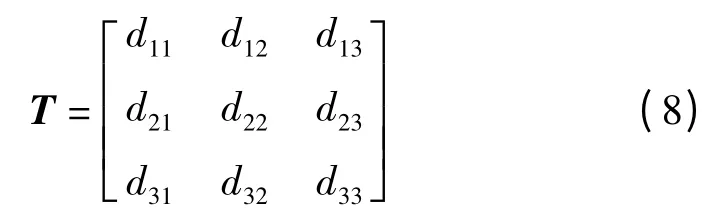
式中:T—动平台姿态的方向余弦矩阵，第1，2，3 列—动坐标系中X'，Y'，Z'轴在固定坐标系中的方向余弦。bo，T—动坐标系相对于固定坐标系的位置和姿态。

在生态城市建设中，首要目标是为人们提供良好的生活和旅游环境。相关部门要建设公共环境，有目的地策划各区的旅游景点，让大家能够在休闲时光里充分放松，缓解平时工作和生活带来的工作压力，使大家保持愉悦的心情[1]。

在式(8)中，矩阵T 虽然有9 个元素，但它们皆依赖于上平台的动坐标系相对于固定平台的定坐标系的3 个独立的转角αb，βb，γb。坐标转换示意图如图5 所示，设绕X 轴旋转的角度用αb表示，绕Y 轴旋转的角度用βb表示，绕Z 轴旋转的角度用γb表示，动、静平台的相对坐标系是先绕X 轴旋转了αb，再绕y 轴旋转了βb，最后又绕Z 轴旋转了γb，则动平台相对于静平台的旋转变换矩阵T 可以表示为:

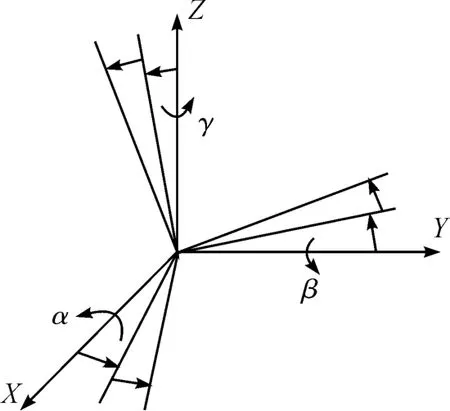
图5 坐标转换示意图

其中:

计算得:

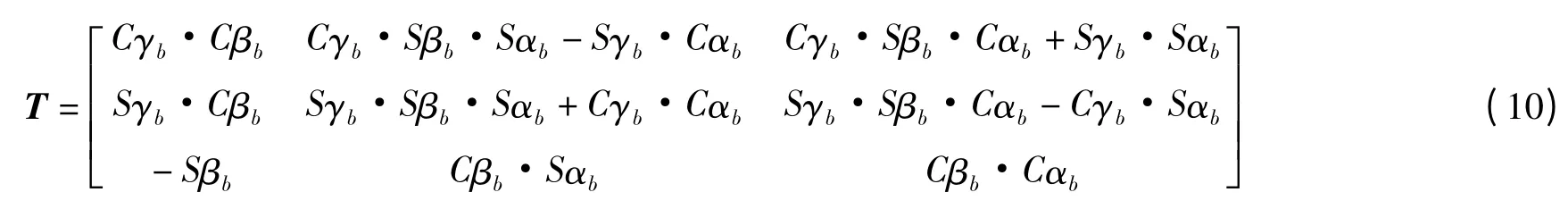
(注:C=cos，S=sin)

再由两点之间的距离公式得到钢带长度:

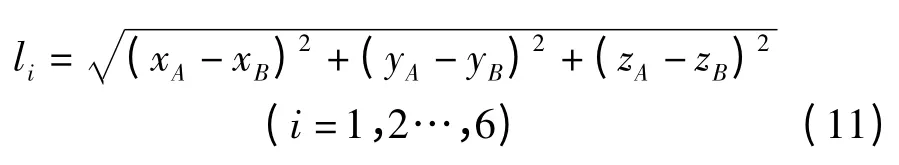
3 实例分析

根据以上理论，现用该超声检测机器人检测一个半径为300 mm 圆环工件中的焊缝，设置超声检测机器人动平台初始位置在z =－800 mm 的平面，动平台外接圆半径r=40 mm，定平台外接圆半径R=400 mm。在检测过程中，超声探头需始终与工件表面垂直，即动平台的β 需实时变化。机器人动平台与被检测焊缝相对位置如图6 所示。

针对已知曲面进行超声检测前，需对超声检测路径进行规划。本研究引用文献［12］中提出的z-map 路径规划原理，利用Matlab 对曲面进行超声检测路径进行规划，得到的路径如图7 所示。图7 中各点为实际超声扫查点。

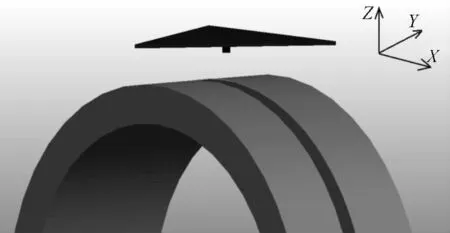
图6 超声检测探头与被检测工件相对位置

得到路径规划图之后，本研究通过控制并联机器人各钢带的长度来最终控制超声探头的位姿。笔者利用Matlab 计算仿真，进一步得到在检测过程中各钢带长度变化曲线如图8 所示。

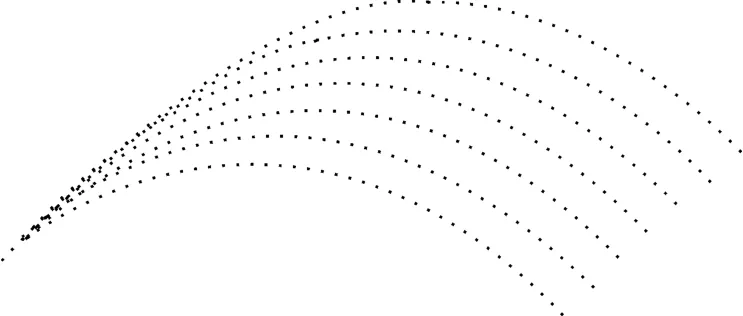
图7 超声检测路径规划图

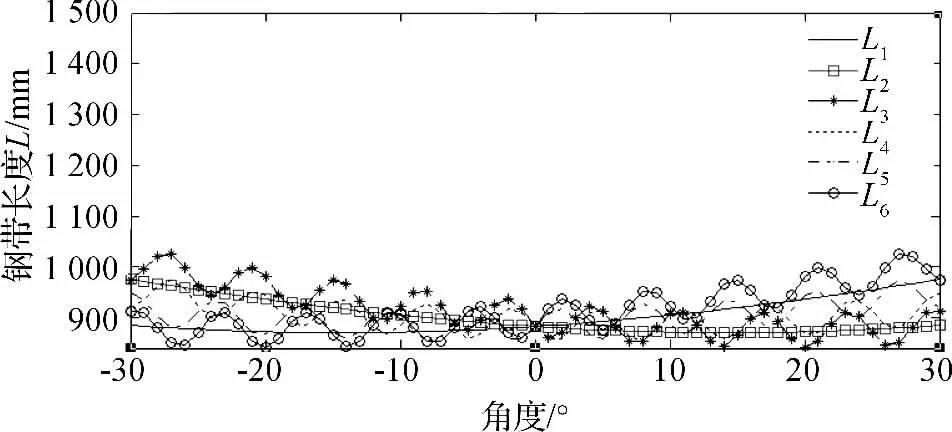
图8 各钢带长度在检测过程中的变化曲线

图8 中，L1和L2与其他4 根钢带变化不同，为正弦变化，这是因为动平台上B1点只做圆周运动，而B2、B3点在大趋势是正弦变化的同时又要实时调整以满足探头位姿始终垂直于焊缝表面。所以在正弦变化的基础上有波动。在角度为0 的位置，各钢带长度相等，此处正好是动平台初始位置，说明建模正确，姿态分析算法可行。

本研究分别采用手工超声检测、串联机器人超声检测和并联机器人超声检测3 种不同的超声扫查方式检测同一工件，检测得到的C 扫查图像如图9～11 所示。不同超声扫查方式黑色噪声所占面积比如表1 所示。其中工件中内置了直径1 mm 的小孔缺陷。对比上述3 张图像，图9 的噪声最大，图中黑色点表示噪声，通过Matlab 计算，图9 中黑色噪声占总面积的36．72%。对检测造成了非常大的影响，中间白色区域为人为设置的小孔，虽然能检测到小孔，但小孔边缘模糊。图10 的噪声相对减少很多，计算得到黑色噪声占总面积的14．96%，小孔的形状也清晰了不少，而图10的小孔形状基本还原了圆形。而且比图11 的噪声也更小，图11 的黑色噪声所占面积比为9．11%。所以综合以上实验数据，将超声检测与并联机器人技术结合，能有效提高曲面超声检测精确度，对结果有积极作用。

表1不同超声扫查方式黑色噪声所占面积比

图9 手工超声检测工件C 扫查图像

图10 串联机器人超声检测工件C 扫查图像

图11 并联机器人超声检测工件C 扫查图像

4 结束语

本研究通过分析超声检测并联机器人的运动学模型，提出了超声背散射检测与并联机器人一体化技术。

通过实验发现，相比超声检测串联机器人更小的末端误差，超声检测并联机器人从硬件上进一步降低超声检测过程中噪声的影响，为从超声信号中提取有用信息提供硬件保障。笔者通过超声检测并联机器人位姿分析，建立超声检测并联机器人的数学模型，利用动坐标系与固定坐标系之间的坐标转换关系，为超声检测并联机器人检测工件的位姿控制提供一种算法。

Matlab 仿真验证了该模型的正确性，且该方法具有算法简单、柔性好等优点，为超声检测过程自动化水平的进一步提升打好基础。

［1］马 俊． 数控机床超声检测系统产品族CAE 技术分析［D］．太原:中北大学机械与动力工程学院，2014．

［2］邱宝梅．超声检测机械手的研制［D］． 西安:西安科技大学机械工程学院，2004．

［3］王艳颖，周晓军． 自由曲面超声检测机器人运动学分析［J］．机电工程，2001，18(5):71-74．

［4］杜兴吉，陈继芳，江 健，等．基于B 样条的自由曲面超声自动检测轨迹生成［J］． 组合机床与自动化加工技术，2004(4):35-37．

［5］吴瑞明，周晓军，徐志农．超声检测机器人误差补偿技术［J］．传感技术学报，2005(2):406-409．

［6］郑慧峰，周晓军，李雄兵．基于本体多关节的超声检测机器人误差补偿［J］．农业机械学报，2008(4):164-167．

［7］DU Hua-long，LONSDALE C，BRENT J O，et al． Evaluation of railroad wheel steel with lamellar duplex microstructures using diffuse ultrasonic backscatter［J］．J Nondestruct Eval，2013，32(4):331-340．

［8］GHOSHAL G． Diffuse Ultrasonic Scattering In Heterogeneous Media［D］． Lincoln:University of Nebraska-Lincoln，2008．

［9］艾青林，祖顺江，胥 芳．并联机构运动学与奇异性研究进展［J］．浙江大学学报:工学版，2012，46(8):1345-1359．

［10］戴 巍．6 自由度并联机器人运动学分析［D］．南京:东华大学机械工程学院，2006．

［11］于 蓬，张为春，裴宝浩．抢险机器人手臂机液耦合仿真分析［J］．液压气动与密封，2011(6):29-33．

［12］姜金为，吴瑞明，刘云峰．基于Z-map 理论的曲面超声自动检测轨迹生成［J］．无损检测，2013，35(9):16-17．