汽车发动机磁流变悬置动特性及PID控制研究*

潘公宇，王倩倩，杨 欣

(江苏大学汽车与交通工程学院，江苏镇江212013)

0 引 言

随着汽车工业的飞速发展，汽车的车型逐步向高功率发动机、轻量化车身等趋势上发展，但这同时也加剧了汽车的振动，影响了汽车乘坐舒适性。而发动机的振动对汽车NVH 有着很大的影响，所以发动机悬置作为连接发动机和车辆底盘的隔振部件，它的隔振效果对整车的振动和乘坐舒适性有直接影响。传统的被动悬置元件已经不能满足发动机在其频率范围内的理想隔振要求，而智能材料和被动悬置元件的结合有效地解决了这一方面的难题，在此背景下半主动悬置逐步应用于发动机悬置系统中［1］。

磁流变液体属于一种可控流体，在磁场作用下可以实现黏度大幅增加，并表现出固体所特有的屈服现象，磁流变液具有连续、可逆调节，反映时间在毫秒级，易于控制的特点［2］。目前国内外对磁流变液在汽车上减震的应用主要有磁流变液减震器和磁流变液悬置，对于磁流变悬置的研究主要有基于流动模式、剪切模式和挤压模式的单惯性通道的发动机悬置［3］。

理想的发动机悬置是为了有效衰减因路面和发动机怠速燃气压力不均匀引起的低频大振幅振动。四缸发动机怠速时的二阶激振频率通常在25 Hz～30 Hz 范围内(对应的怠速转速为750 r/min～900 r/min)，为了减少由发动机的激励而导致的转向盘、变速杆等系统的振动，希望在发动机怠速转速附近，悬置系统具有较小的刚度，此时需要悬置具有较大的滞后角峰值频率(20 Hz 以上)。本研究试图在已有磁流变半主动悬置的基础上改进悬置结构，设计一种多惯性通道的磁流变悬置，目的是更好地满足发动机悬置在怠速工况下的理想隔振要求。

本研究针对这一新型结构的磁流变悬置，从理论推导方面得出并分析该悬置的动刚度和阻尼滞后角曲线，并通过试验对单惯性通道悬置模型进行验证，建立带有3 个惯性通道的磁流变悬置的控制模型，预测磁流变液悬置的隔振效果。

1 磁流变悬置结构及动特性公式推导

1．1 磁流变悬置结构

一般发动机磁流变半主动悬置采用的结构简图如图1 所示［4］。

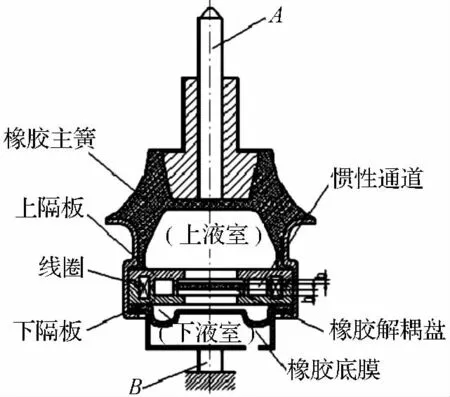
图1 磁流变悬置结构图

该磁流变悬置的工作原理:上液室由橡胶主簧、线圈座、导磁通道体以及惯性通道体上部组成，下液室由橡胶底膜、线圈座、导磁通道体以及惯性通道体下部组成。当悬置受到向下的激励时，橡胶主簧被压缩，上液室体积缩小，上液室的磁流变液体受压力作用通过惯性通道流向下液室，此时橡胶底膜利用自身的弹性特性承受由橡胶主簧引起的上、下液室体积的变化，在磁流变液体流经惯性通道时，作用在惯性通道中磁场强度发生变化，使得悬置产生最优阻尼力。

1．2 磁流变悬置动特性公式推导

本研究主要针对悬置的低频、大振幅的振动进行研究，该工况下，液体主要经过惯性通道在上、下液室间交换，可以认为解耦通道没有液体流动，所以可忽略解耦膜的影响。

参照磁流变悬置的结构图，简化结构，本研究建立的带有多个惯性通道的磁流变悬置集总参数的力学模型［5］如图2 所示。

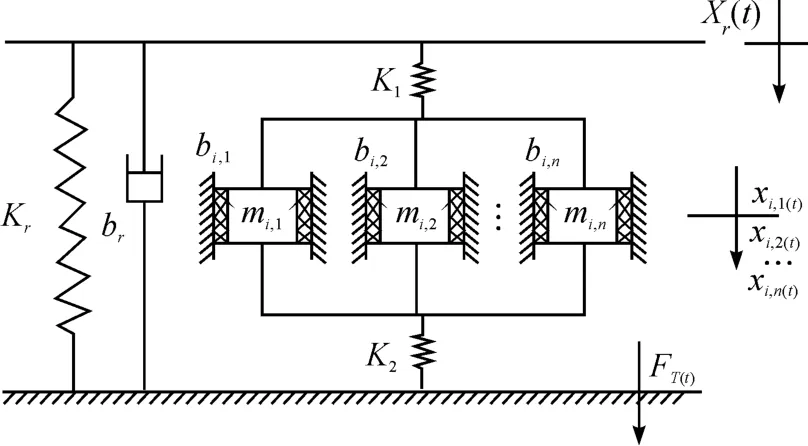
图2 多惯性通道磁流变悬置的力学模型

根据图2 的力学模型，建立系统的平衡方程:

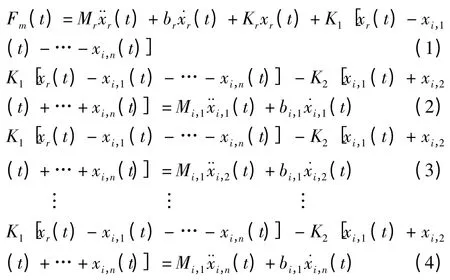
式中:Fm(t)—发动机产生的激振力;Mr—橡胶主簧的质量。Fm(t)—输入;xr(t)—输出。对上述方程进行拉普拉斯变换，令s=jω，得到如下矩阵:

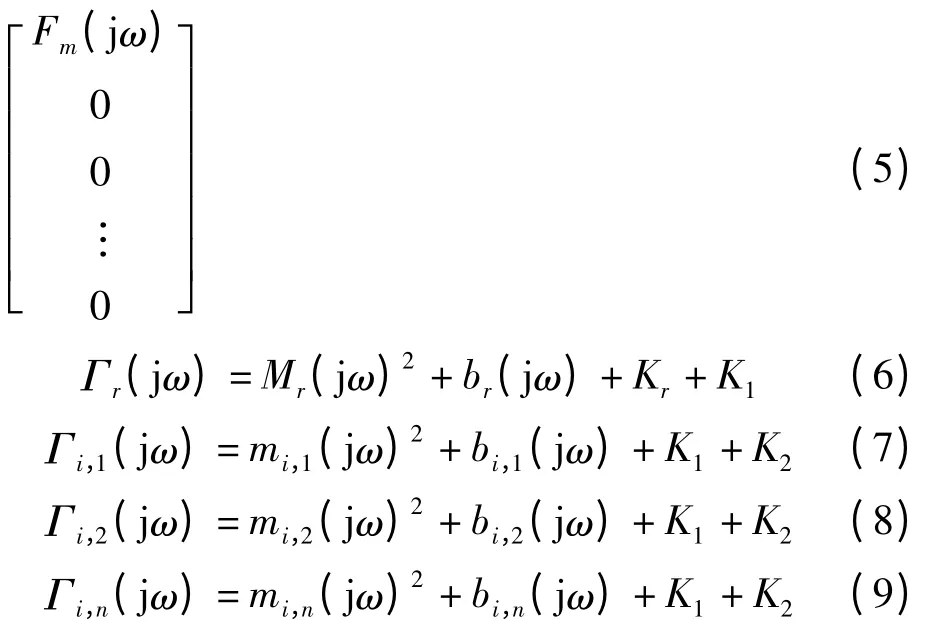
为使模型能突出悬置动特性的主要影响因素，同时具有足够的精确性，本研究进行了如下的假设:

(1)忽略橡胶主簧质量，即Mr=0。橡胶主簧本身是一种粘弹性元件，具有一定的非线性。出于橡胶材料的驻波效应，使得高频动刚度剧烈增加，此时橡胶主簧自身质量的影响是不可忽视的。但在中低频段的研究中，忽略其质量是合理的。

(2)下液室的体积刚度K2远小于上液室的体积刚度K1，对悬置动特性的影响较小，可忽略不计。

(3)橡胶主簧的阻尼br很小，对悬置动特性的影响较小，可以忽略不计。

对于n=1 的单惯性通道悬置，有:

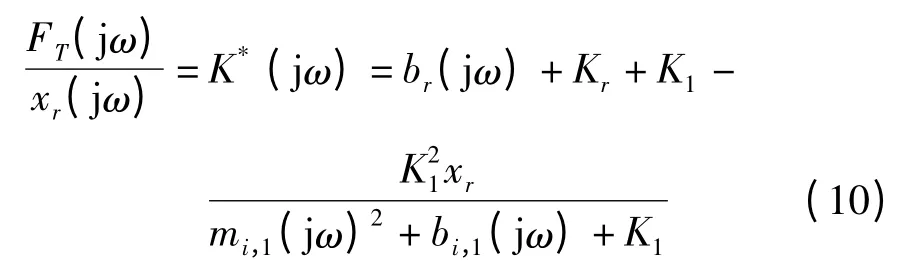
对于n≥2 的多惯性通道悬置，有:

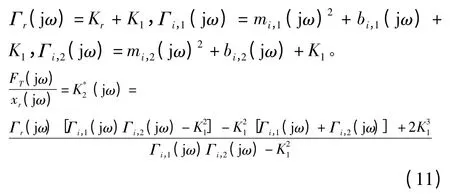
引入xeq(t)=xi，1(t)+xi，2(t)这个表达式，液压元素的特征方程可以表示为α(jω)= meq(jω)2+beq(jω)+K1，扩展这个概念，对于带有n 个惯性通道的磁流变悬置参数定义如下:

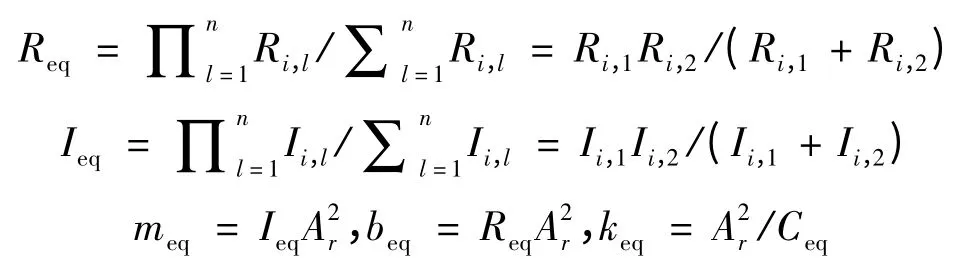
代入上述方程得到:

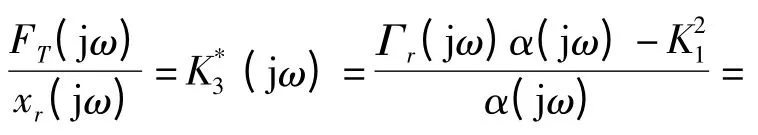
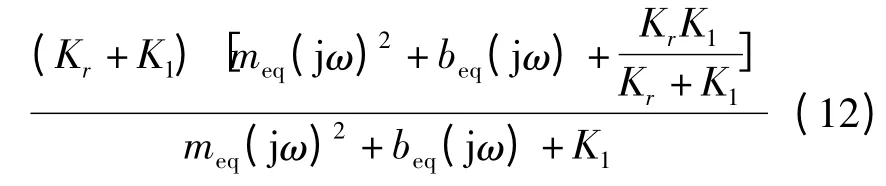
则有:

本研究主要研究的是带有n 个相同惯性通道的磁流变悬置，通过计算得到:

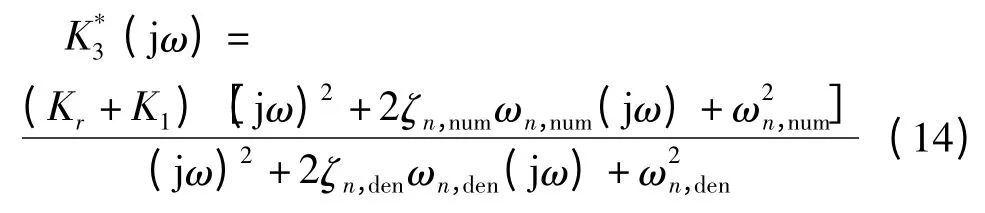
其中:

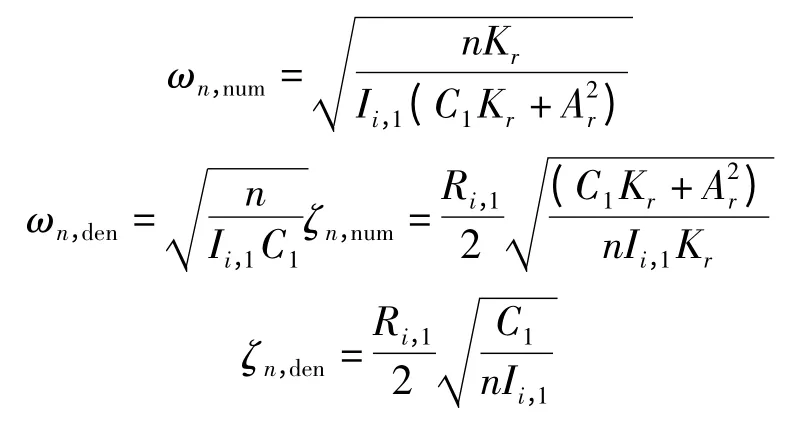
2 磁流悬置动特性仿真及试验

2．1 磁流变悬置动特性仿真

为了计算该磁流变悬置的动刚度与滞后角曲线，本研究参考前人研究的成果，选取其集总参数为:橡胶主簧刚度Kr=2．5 ×105N/m，上液室体积柔度C1=3 ×10-11m5/N，橡胶主簧等效面积Ap=2×10-3m2，惯性通道截面宽度a =7 ×10-3m，惯性通道截面高度b =8 ×10-3m，惯性通道直径d =0．026 m，惯性通道截面积Ar=ab，惯性通道长度l =0．118 m，磁流变液液体密度ρ= 3 540 kg． m-3，液体零场粘度 μ = 3． 67 ×10-2Ns2/m5;惯性通道液体阻尼Ri=128μl/πd4+ lτy(a+b)/vApab，惯性通道液体液感Ii=ρl/ab，上液室体积等效刚度K1=1/C1。

本研究利用软件对上述公式进行程序编制分别计算单惯性通道磁流变悬置和多惯性通道磁流变悬置的动刚度和滞后角。对于单惯性通道磁流变悬置，其频率范围取0～50 Hz，激励振幅取0．5 mm，电流分别取0 A、0．5 A 和1 A，其计算结果如图3 所示。

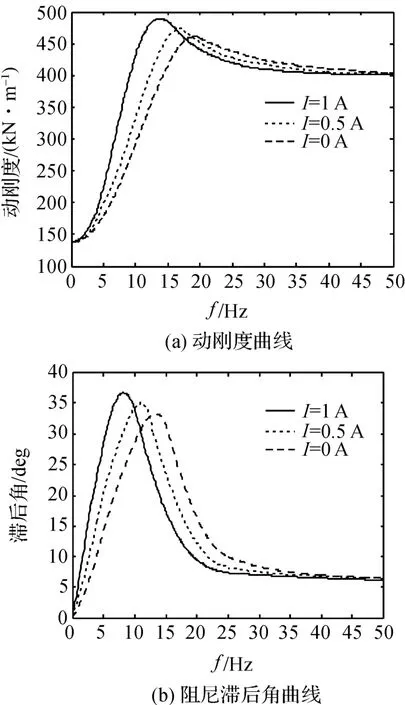
图3 单惯性通道磁流变悬置的动刚度和阻尼滞后角曲线

由图3 可以看出，无论如何改变电流，单惯性通道磁流变悬置在低频段的动刚度峰值频率处于13 Hz～20 Hz 之间，阻尼滞后角峰值频率处于7 Hz～15 Hz 之间，没有满足发动机悬置在怠速工况下的理想隔振要求，因而不能有效地衰减发动机的低频振动。现在考虑从惯性通道的个数入手，研究其低频峰值频率。

对于多惯性通道磁流变悬置，为了方便观察，本研究只考虑电流取1 A，频率范围取0～50 Hz，激励振幅取0．5 mm时的情况，其计算结果如图4 所示。

由图4 可以看出，随着惯性通道数目的增加，动刚度和阻尼滞后角峰值大小及所对应频率均增大。当n=3时，在频率0～20 Hz 之间，悬置系统具有较小的刚度，滞后角峰值频率在24 Hz 左右。当n =4 时，在频率0～25 Hz 之间，悬置系统具有较小的刚度，滞后角峰值频率在29 Hz 左右，均满足了在发动机怠速转速附近，悬置具有较大的滞后角峰值频率的要求。

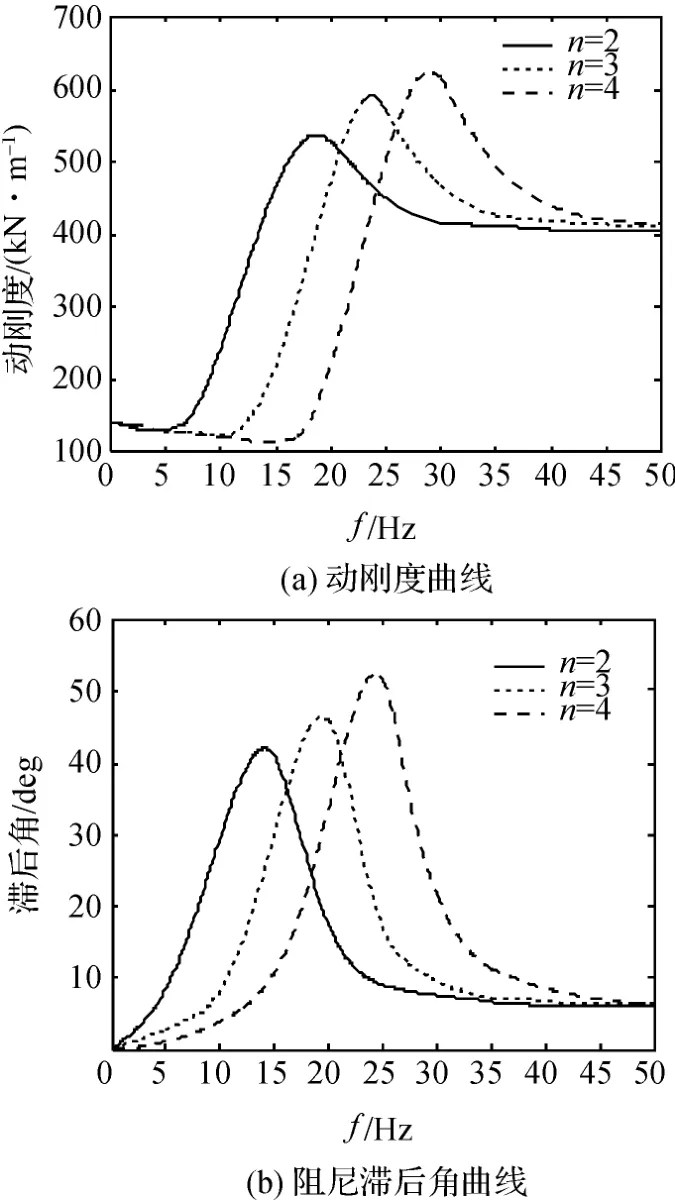
图4 多惯性通道磁流变悬置的动刚度和阻尼滞后角曲线

2．2 试验

为了验证悬置模型结构的正确性，本研究在MTS激振控制台架上对单惯性通道磁流变悬置进行了验证实验［6］，测试现场如图5 所示。笔者对于该实验选用的磁流变悬置，其怠速频率为24．5 Hz，是电液伺服系统需要激发的特征点。同时在垂直方向上加载500 N，电流分别为0 A、0．5 A 和1 A，激励频率分别取1，5，10，15，20，24．5，30，35 Hz，激励振幅为0． 5 mm 和0．25 mm的情况下进行试验。

图5 磁流变悬置实验台架

本研究通过对两组实验数据的处理，得到两种工况下的实验曲线图。

在预载荷为500 N，激励振幅分别为0．5 mm 和0．25 mm的低频段工况下得到的的不同电流输入的实验曲线图分别如图6、图7 所示。从实验结果中得出:

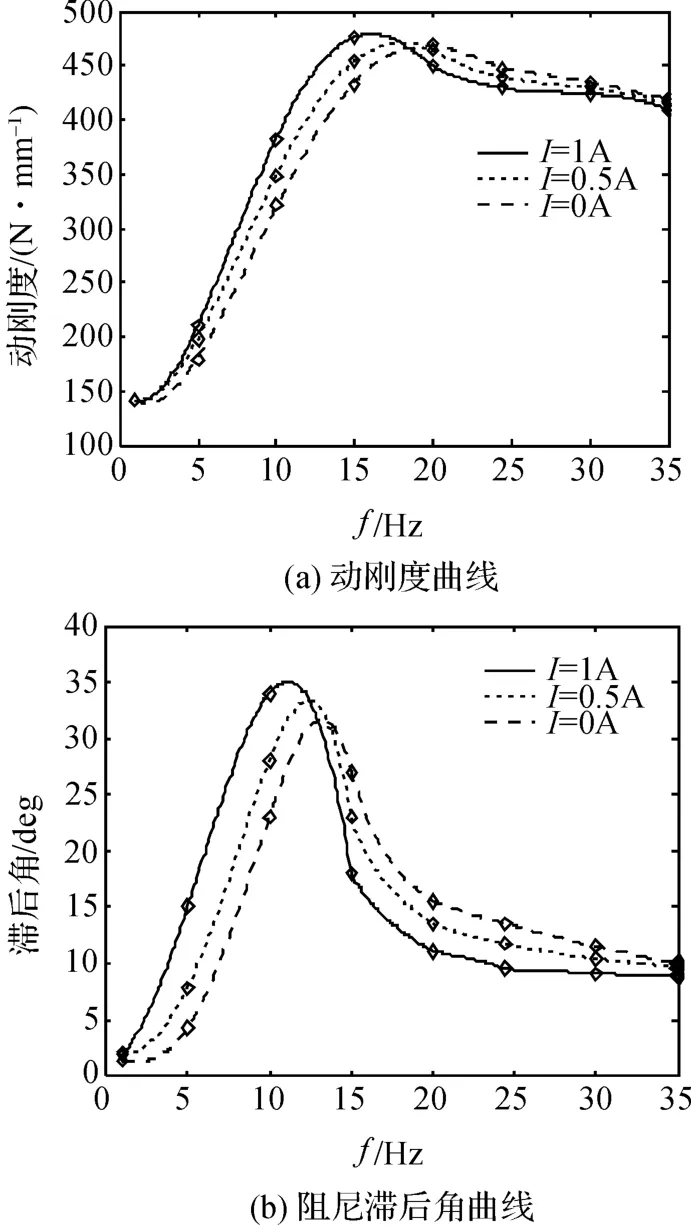
图6 预载500 N，振幅0．5 mm 的实验结果图

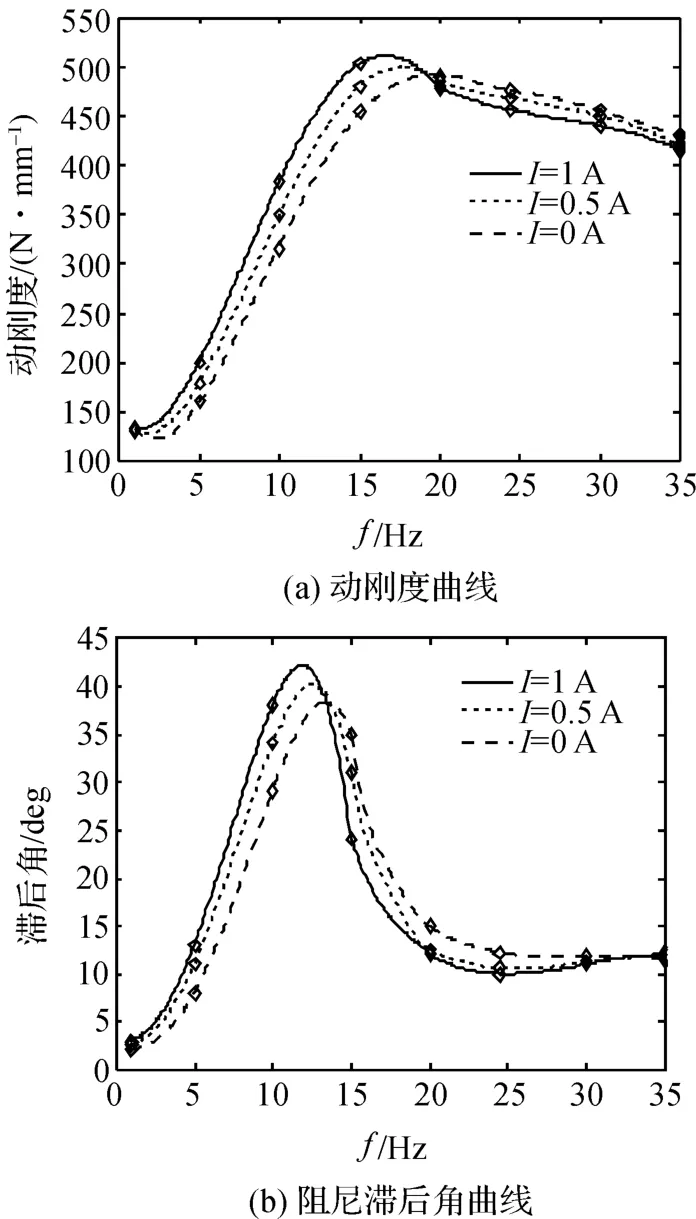
图7 预载500 N，振幅0．25 mm 的实验结果图

总的来说，在0～35 Hz 时，磁流变悬置的动刚度和滞后角都有很明显的非线性特性，动刚度在15 Hz 左右到达峰值，滞后角在12 Hz 左右达到峰值，随着施加电流的变大，峰值频率略微有所减小，峰值略微增大。而且这个结果与图3 的单通道磁流变悬置低频段仿真结果相近，从而验证了单惯性通道磁流变悬置建模理论的正确性。

3 磁流变悬置PID 控制

3．1 二自由度磁流变悬置系统模型

本研究对带有3 个惯性通道的磁流变悬置进行隔振研究，主要针对垂向振动，考虑悬架的等效刚度和阻尼，将悬置系统简化为垂直方向的二自由度模型［7-8］，三自由度磁流变悬置系统模型如图8 所示。由于主要研究磁流变悬置怠速工况下隔离发动机振动的性能，故该模型不考虑路面不平度的输入。

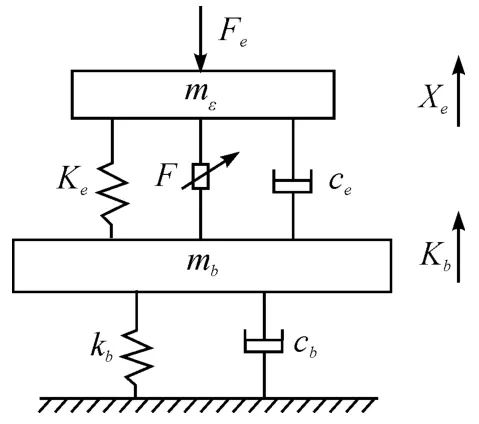
图8 三自由度磁流变悬置系统模型

根据图8 的数学模型，应用牛顿定律，可得到其振动微分方程。

发动机等效质量振动方程:

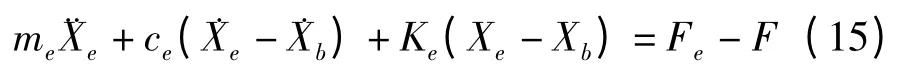
车身等效质量振动方程:

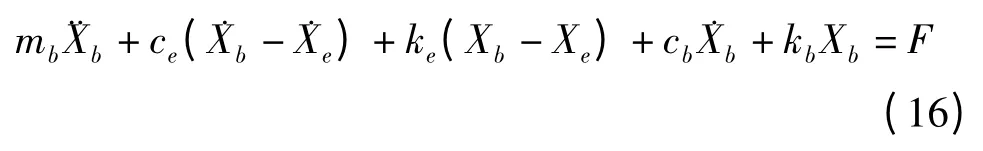
取Fe为发动机二阶往复惯性力:

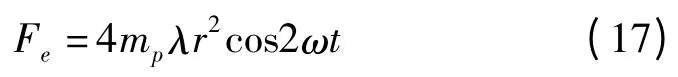
式中:ω—曲柄角速度，ω =2πn/60;n—转速;mp—活塞质量;r—曲柄半径;λ—曲柄连杆长度比。

根据上述方程，选取状态向量:

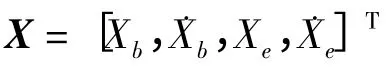
系统状态方程为:

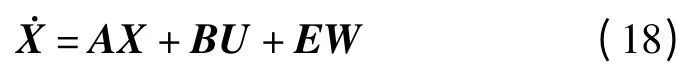
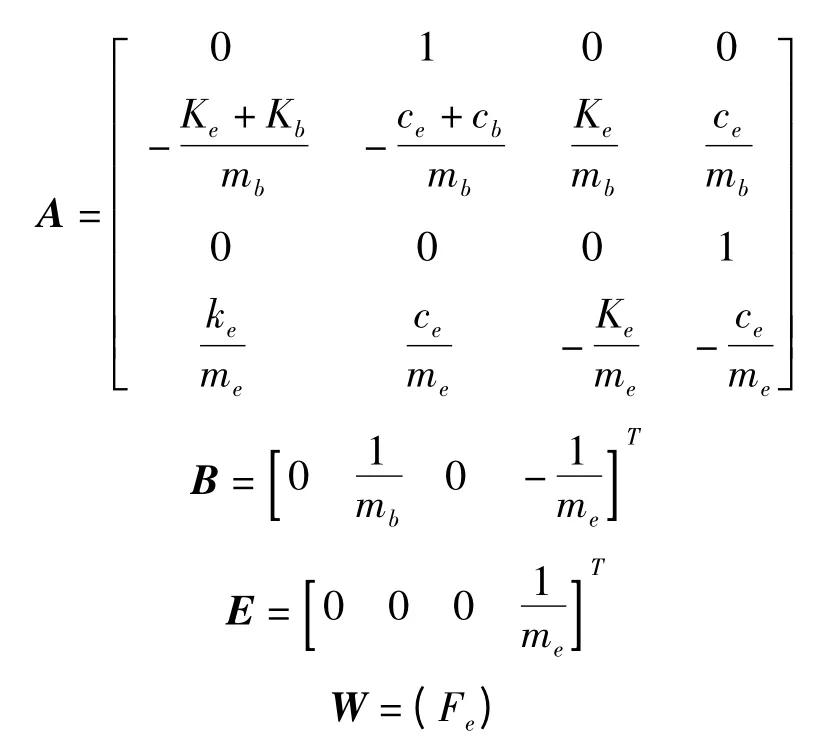
控制量U 为可控阻尼力F，选取输出向量:

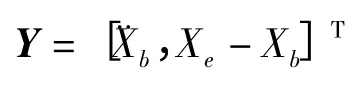
则:

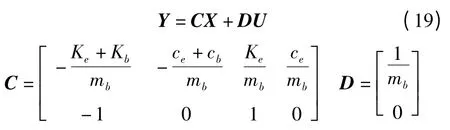
3．2 磁流变悬置的PID 控制仿真

本研究采用PID 控制方法［9］对半主动磁流变悬置实施控制。以车身振动的加速度和设定值(为0)之间的偏差作为输入，控制目标是减小车身加速度，从而实现磁流变悬置的隔振作用。本研究使用试凑法来确定PID 控制器参数。经过多次整定后，找出一组最佳控制参数。

本研究在Matlab/Simulink 中建立仿真模型［10-11］，仿真过程中，取发动机怠速工况下的激振力。PID 控制器的比例增益为200，微分增益为0．06，积分增益为3。考虑的评价指标主要有车身质心加速度和悬置动行程，得到仿真结果如图9、图10 所示。

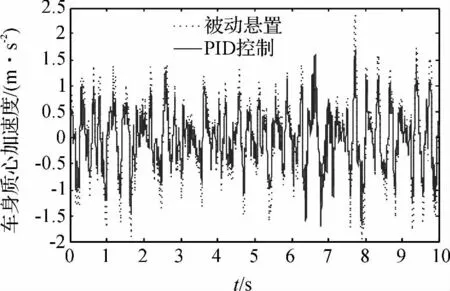
图9 车身质心加速度

由图9、图10 可以看到，当磁流变悬置采取半主动控制后，车身质心加速度和悬置动行程都有一定的改善。为了更明确地反映磁流变悬置在采用半主动控制后，其隔振性能改善的程度，现将仿真结果按照aw=计算加速度和动行程的均方根值，以便定量分析其平顺性性能。根据该公式，笔者求得的两个评价指标的均方根值如表1 所示。

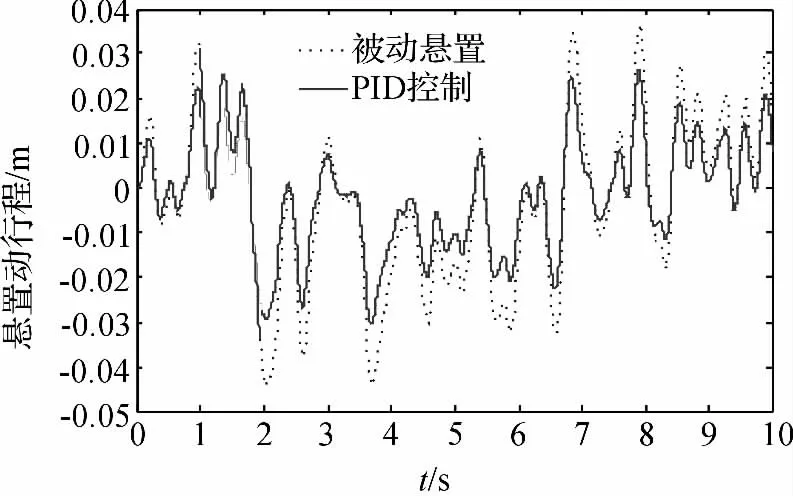
图10 悬置动行程

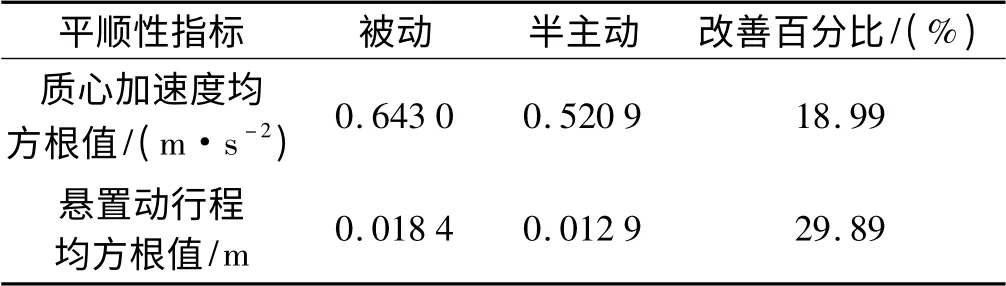
表1 平顺性评价指标均方根值表

从表1 中可以看出，磁流变悬置在采取了PID 控制后，车身质心加速度和悬置动行程分别减小了18．99%和29．89%。

4 结束语

本研究借助Matlab/Simulink 搭建仿真模块，对悬置结构进行了仿真分析，得到以下结论:

(1)本研究通过增加惯性通道个数来增大动刚度和阻尼滞后角的峰值频率，当n =3，4 时，在频率0～20 Hz 之间，悬置系统具有较小的刚度，且滞后角峰值频率在20 Hz 之后，满足了在发动机怠速转速附近，悬置具有较大的滞后角峰值频率的要求。

(2)本研究仅对单惯性通道磁流变悬置进行了试验研究，研究结果表明，理论仿真和试验结果基本吻合，说明理论建模方法是合理的。

(3)本研究采用PID 控制方法对包含发动机-车身在内的二自由度系统在发动机怠速工况下的隔振特性进行了半主动控制仿真，研究结果表明，磁流变悬置在采取了PID 控制后，车身质心加速度和悬置动行程分别减小了18．99%和29．89%，因此该磁流变悬置可以较好地解决发动机隔振问题。

［1］浦鸿汀，蒋峰景． 磁流变液材料的研究进展和应用前景［J］．化工进展，2005，24(2):132-136．

［2］司 鹄，彭向和．磁流变材料的流变性能研究［J］．材料科学与工程，2002，20(1):61-63．

［3］章新杰．磁流变挤压悬置动态特性研究及其在汽车中的仿真应用［D］．长春:吉林大学汽车学院，2011．

［4］王雪婧．磁流变半主动发动机悬置隔振性能与控制方法研究［D］．长春:吉林大学汽车学院，2011．

［5］周昌水，邓兆祥，孙登兴．动力总成悬置系统建模与性能优化［J］．重庆大学学报:自然科学版，2007，29(11):23-26．

［6］吕振华，上官文斌．液阻悬置动态特性实验方法及实测分析［J］．中国机械工程，2004，15(2):182-186．

［7］王永达，许沧粟．发动机振动模糊半主动控制的研究［J］．汽车工程，2006，28(7):663-666．

［8］李 锐，陈伟民．发动机磁流变悬置隔振模糊控制与仿真［J］．系统仿真学报，2009，21(4):944-953．

［9］仇成群，刘成林． 基于Matlab 和模糊PID 的汽车巡航控制系统设计［J］．农业工程学报，2012，28(6):197-202．

［10］王国玲，李振宇，范自道．无刷直流电机自适应模糊PID控制系统［J］．机电工程技术，2013(2):37-40．

［11］HONG S R，CHOI S B，CHOI Y T，et al． Ahydro-mechanical model for hysteretic damping force prediction of ER damper:Experimental verification［J］． Journal of Sound and Vibration，2005，285(4/5):1180-1188．

［12］BRIGLEY M，CHOI Y T，WERELEY N M，et al． Magneto-rheological isolators using multiple fluid modes［J］．Journal of Intelligent Material Systems And Structures，2007(18):1143-1148．