犯罪案件移动平均预测模型改进研究

王璟瑶，　秦　静，　刘　军

(中国人民公安大学警务信息工程学院， 北京　100038)

犯罪案件移动平均预测模型改进研究

王璟瑶，秦静，刘军

(中国人民公安大学警务信息工程学院， 北京100038)

摘要目的 建立一个针对犯罪案件的数量预测模型，从而根据案发态势科学运用警力，有效实现犯罪预防。方法 基于移动平均方法预测，并对其加以改进，添加误差负反馈环节，对预测模型实行闭环控制。结果 改进后的移动平均模型均方误差明显减小，预测值的自动跟踪效果更佳。

关键词移动平均； 犯罪预测； 闭环控制

0引言

科学准确地预测犯罪是公安机关在预防与控制犯罪方面的工作重点之一，也是警力合理部署的重要工作手段。犯罪预测是指依据一定历史时期或现有的犯罪数据，运用科学方法分析研究时间、空间因素和经济、人口等社会背景因素对犯罪影响的可能性和程度大小，从而对城市、乡镇及其各辖区未来可能出现的犯罪数量或类型做出趋势性的判断。随着公安信息化进程的不断加快，公安工作的重心已从被动地严厉打击与处罚逐渐转移到靠主动出击进行犯罪预防，最大程度上将犯罪扼杀在摇篮中。

犯罪预测是预防犯罪的基本前提，缺乏科学准确的犯罪预测，犯罪预防则无从谈起。我国在犯罪预测及其研究发展上尤显滞后，技术欠缺，致使预测脱离实际公安需求。移动平均法预测是当前短、中期预测的常用方法之一，根据时间序列数据逐期推移预测，计算简单，对于波动性不大的平稳时间序列，准确度较高，但是对于因季节等相关因素突发波动的数据序列，则准确度欠佳。

本文对简单移动平均模型加以改进，添加了负反馈环节，并考虑了季节因素对犯罪预测结果的影响，通过误差范围不断调节调整系数，以实现误差自动校正，预测值向实际值拟合得更接近。

1移动平均预测模型概述

1.1　移动平均预测模型的概念

移动平均预测模型是根据近期的实际案发数据值通过推移平均计算来预测未来一段时间的案件发生量的预测方法。将历史案发数据整理成时间序列，逐期推移计算每个时期的犯罪数量平均值，从而反映出所选研究范围在未来一定时期内的犯罪趋势。

1.2　移动平均预测模型的分类

根据预测时序列中各时期元素的权重差异，可将移动平均预测方法分为简单移动平均和加权移动平均。二者最大的不同之处在于前者各元素权重均相等，其计算公式[1]如下：

(1)

其中Yt为t时刻的预测值，n为移动平均的时期个数，Xt-1，Xt-2,…,Xt-n分别表示t时刻前一期、前两期直至前n期的实际值。

而加权移动平均法的计算方法则为：

(2)

其中ω1…ωn分别为各历史时期相应的权重值，且ω1+ω2+…+ωn=1。

考虑到历史各期的案发数据信息对预测未来期内的作用不一样，加权移动平均给予每个变量值的权重不相等。与远期数据相比，离预测期较近的实际值的犯罪影响力较高，在预测运算中设定的权重值则应当较大。

1.3　移动平均预测的特点与不足

移动平均预测的最大特点是若不考虑季节性因素，且当案发量没有呈现出速升或速降的趋势时，可以通过此方法来消除时间序列中的季节波动和随机变动，从而能够直观地反映出该序列的长期趋势。因此，它更适用于短期预测，尤其是以月或周为单位的近期预测[2]。

通过移动平均法预测案发值的好处是可以平滑掉因时间序列的突然波动对预测结果产生的误差影响，但另一方面该方法也有一定的局限性：

(1)增加移动平均的时距(即n值)会使时间序列的平滑效果较好，然而同时会造成预测值与实际数据的偏差更大；

(2)由于预测值是各历史时期的平均值，因而预测结果受历史时间因素影响较大，并不能总是与未来的实际高低波动保持一致；

(3)各历史时期值在进行移动平滑时权重并不是一成不变的，具体如何调整也要受当前几期的实际值的影响。

2基于闭环控制理论的移动平均预测模型改进方法

移动平均是一种开环控制预测方法，并不能随时消除干扰所带来的误差影响。因此，本文在预测模型中添加了负反馈环节，构成了一个闭环控制模型，通过对调整参数的设定和改变，从而实现参数的自动控制，提高预测的准确度和稳定性。

2.1　移动平均负反馈预测模型及工作原理

基于闭环控制理论的移动平均负反馈预测模型如下方框图所示。

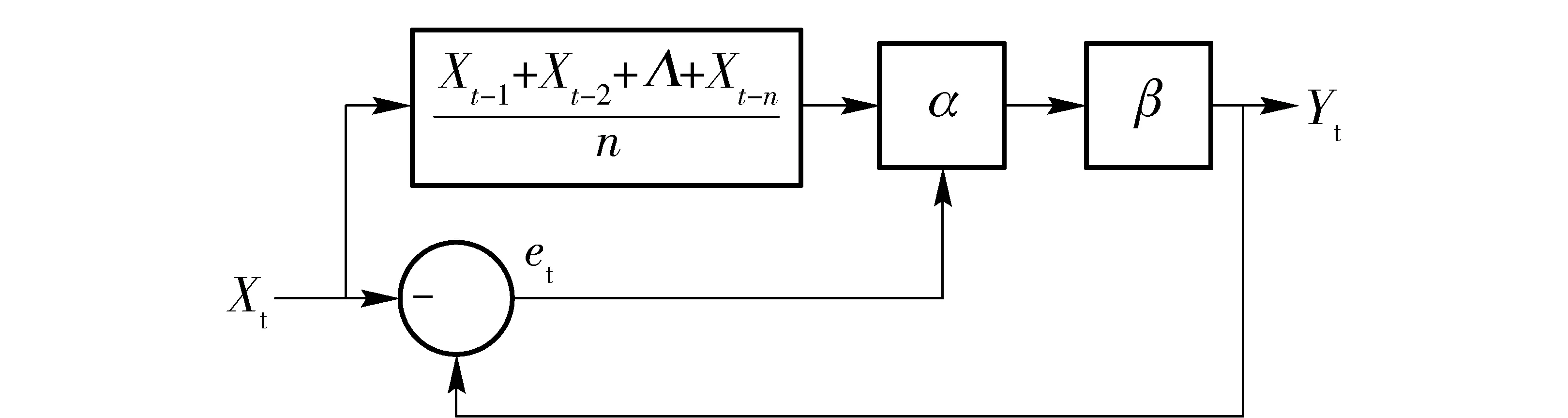
图1　移动平均负反馈预测模型框图

当预测t时刻的案发值时，可以通过简单移动平均法的计算公式(1)计算获得，再将计算出来的均值乘以调整系数α和季节指数β，得到t时刻的预测值Yt，并与t时刻的实际值Xt相减得到误差值et。通过判别et的正负大小来调节α，以实现下一时刻的跟踪预测。

2.2　参数的计算和调整方法

2.2.1季节指数β的确定方法

随着季节与月份的时间性变化，犯罪类型和犯罪数量的变化趋势也表现出不同程度的波动。从刑事案件发案规律统计来看，春夏季人身犯罪偏多，秋冬季财产犯罪偏多。原因是一方面季节变化对人们的社会经济活动、生活节奏产生的影响，相应地刑事犯罪活动也随之变化，从而表现出案发的季节性规律；另一方面，犯罪分子也会根据作案目的的需要、作案对象的特点，从而选择适合的作案时间。因此，要科学准确地预测犯罪量的多少，必须掌握刑事案件的季节性案发规律，从而有针对性地部署警力，预防、打击犯罪。

本研究以一年12月的案发量为研究周期，根据统计的案件数量以及季节变化的影响，将季节影响参数[3]β在非高发季节设置为1，高发季节可增大调整，从而表现出春、夏、秋、冬四季对犯罪数量不同程度的影响。

2.2.2调节系数α的调整方法

预测值Yt与实际值Xt相减得到的误差值et直接作用于α，从而调整其大小，每次调整后的α值作为下一期的新值参与运算。在添加α环节前，先根据移动平均预测值与实际值之间的误差范围，将其分为五个区间段进行调整。α初始值设为1，若误差et>0，则减小α，反之则增大，具体调整数值范围如表1所示。

表1　α数值调整参数表

3数据拟合

3.1　开环模型拟合结果

本文以某分局某年4月至次年3月共12个月的实际刑事案发量为研究数据，开环模型通过简单移动平均方法预测每月的案件数量，其中开环与闭环模型的移动平均步长N均为3，图2为传统移动平均拟合曲线图。

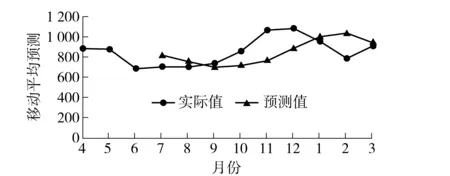
图2　开环模型预测曲线图

从图中可以看出，简单移动平均对数据的平滑效果较好，但并不能很好地反映出数据的波动情况，导致对数据的实时跟踪不明显。因此，本文要对简单移动平均模型加以改进，使预测结果对实际数据进行自动跟踪。

3.2　闭环模型拟合结果

本文向简单移动平均模型加入负反馈环节，通过调整系数来不断减小实际值与预测值之间的误差。各月案发数据预测及调整计算结果如表2所示。

表2　闭环模型各指标数据表

改进模型拟合的曲线如图3所示，与改进前的模型相比，预测值与实际值间的跟踪效果较好。

图3　闭环模型预测曲线图

3.3　模型评价指标

评价预测值与实际值好坏的方法主要有平均绝对误差(MAE)、均方误差(MSE)、平均绝对百分比误差(MAPE)、均方百分比误差(MSPE)[3]4种，本文以均方误差为例，对比模型改进后的预测误差测定，结果如表3所示。

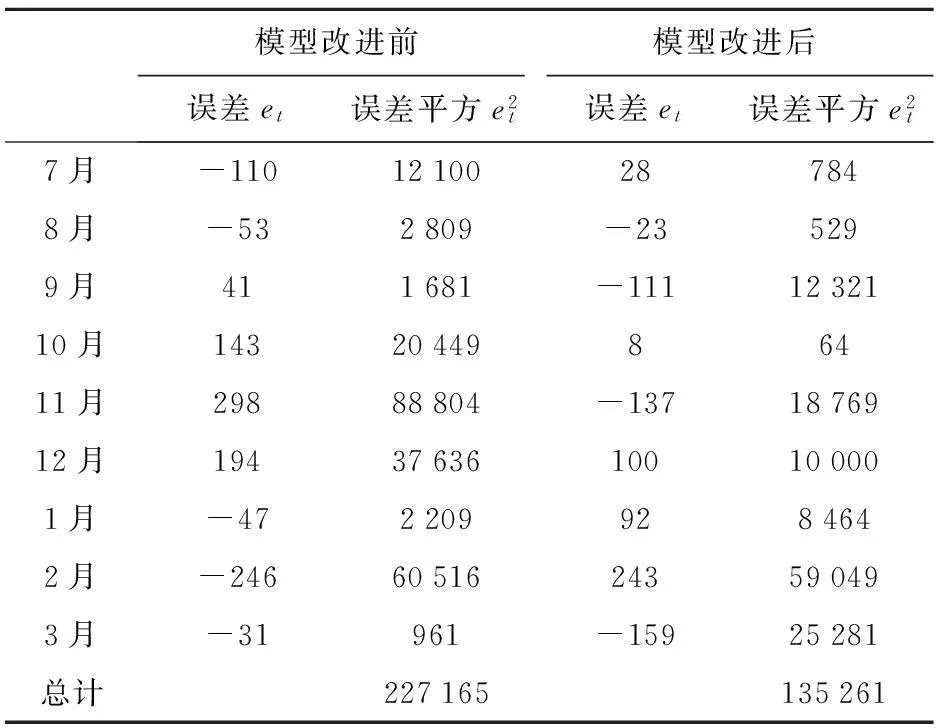
表3　模型改进前后误差对比

(3)

其中Xt是t时刻实际值,Yt是t时刻预测值,N是采样数。

综上表所述，模型改进前MSE前=227 165/9=25 240，模型改进后MSE后=135 261/9=15 029，由此可见模型改进后误差明显减小，跟踪预测效果更佳。

4结论

与传统移动平均模型相比，改进后的模型添加闭环控制环节，充分发挥了反馈的重要作用，只要误差偏离规定范围，就会调整相应系数去消除偏差，提高了模型的自动修正和补偿能力，实现了预测值向实际值的自动跟踪，大大增强了预测的准确性，解决了简单移动平均模型预测对实际数据变动不敏感的问题。同时为公安机关有效预防并遏制犯罪上升以及根据发案态势变化调整警力部署等问题提供了科学方法与理论依据。

参考文献

[1]公安部政治部.公安统计学[M].北京：中国人民公安大学出版社，2008.

[2]刘剑宇，熊允发. 移动平均法在公安情报分析中的应用[J]. 中国人民公安大学学报：自然科学版，2007(4)：54-56.

[3]陈冬冬，彭其渊. 一组预测方法的比较分析[J].计算机工程与应用，2009，45(26)：199-203.

(责任编辑陈小明)

作者简介王璟瑶(1989—)，女，天津人， 2012级硕士研究生。研究方向为警务信息技术。

中图分类号D918