Ultimate load bearing capacity evaluation of concrete beamssubjected to freeze-thaw cycles

Qin Xiaochuan　 Meng Shaoping　 Tu Yongming　 Cao Dafu

(1School of Civil Engineering, Southeast University, Nanjing 210096, China)(2College of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, China)



Ultimate load bearing capacity evaluation of concrete beamssubjected to freeze-thaw cycles

Qin Xiaochuan1Meng Shaoping1Tu Yongming1Cao Dafu2

(1School of Civil Engineering, Southeast University, Nanjing 210096, China)(2College of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, China)

Abstract：A theoretical prediction method based on the change of concrete material is proposed to evaluate the ultimate bending moment of concrete beams which have undergone freeze-thaw cycles (FTCs). First, the freeze-thaw damage on concrete material is analyzed and the residual compressive strength is chosen to indicate the freeze-thaw damage. Then, the equivalent block method is employed to simplify the compressive stress-strain curve of the freeze-thaw damaged concrete and the mathematical expression for the ultimate bending moment is obtained. Comparisons of the predicted results with the test data indicate that the ultimate bending moment of concrete beams affected by FTC attack can be predicted by this proposed method. However, the bond-slip behavior and the randomness of freeze-thaw damage will affect the accuracy of the predicted results, especially when the residual compressive strength is less than 50%.

Key words：concrete beam; freeze-thaw cycles; ultimate bending moment; structural analysis

Received 2015-02-09.

Biographies：Qin Xiaochuan (1985—), male, graduate; Tu Yongming (corresponding author), male, doctor, associate professor, tuyongming@seu.edu.cn.

Foundation items：The National Natural Science Foundation of China (No.50978224, 51378104), the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Citation：Qin Xiaochuan, Meng Shaoping, Tu Yongming, et al. Ultimate load bearing capacity evaluation of concrete beams subjected to freeze-thaw cycles[J].Journal of Southeast University (English Edition),2015,31(4):522-528.[doi:10.3969/j.issn.1003-7985.2015.04.016]

The freeze-thaw cycle (FTC) attack is one of the most severe factors that lead to the durability deterioration of existing reinforced concrete structures in cold regions[1-2]. As FTCs are repeated, the concrete material gradually loses its strength and stiffness with the growth of the internal cracks caused by the volume expansion of freezing water stored in the pore system of concrete[3-4]. Several reports have been focused on the performance of concrete material under FTCs[5-12]. However, little attention was paid to reinforced concrete members and prestressed concrete members[13-15]. For concrete structures, concrete material deterioration will cause load-bearing capacity degradation, which eventually makes the whole structure incapable of service. Thus, there is a growing need for methods to evaluate the freeze-thaw damaged concrete structures. A method for predicting the ultimate load bearing capacity of freeze-thaw damaged concrete structures is proposed, testified and discussed in this paper.

1Foundations of the Prediction Method

1.1　Indicators of freeze-thaw damage

In the assessment of the freeze-thaw damage on concrete, various indicators, such as the relative dynamic modulus of elasticity (RDME), compressive strength and etc., must be measured after a specified number of FTCs.

The RDME is the most popular indicator of freeze-thaw damage in many test standards, such as ASTM C666/C666M-03[16], GB/T 50082—2009[17], etc. The test of RDME is developed from the analysis of a homogeneous rod under free flexural vibration. Thus, it is assumed that the specimen is homogeneous and elastic. However, this assumption is not quite true for concrete material, especially for freeze-thaw damaged concrete material. For undamaged concrete material, as shown in Fig.1(a), the assumption is reasonable because the whole specimen is tightly bound by cementitious materials and the volume ratio of the micro-cracks to the specimen is very low, which means that vibration can be transmitted through the specimen easily. For freeze-thaw damaged concrete material, as shown in Fig.1(b), the situation is different. As FTCs go on, the original micro-cracks will grow larger and new cracks will form. Hence, the specimen will be separated into a few micro-units and cannot be treated as a homogeneous material any more.

Another feasible indicator of freeze-thaw damage is the compressive strength of the freeze-thaw damaged concrete cube. In the compression test, it is appropriate to assume that the undamaged concrete material is homogeneous because the micro-cracks tend to close under compression. When performing the compression test on the freeze-thaw damaged concrete cube, it is still reasonable to believe that the specimen is homogeneous, because some of the cracks induced by FTCs (i.e. horizontal cracks) will first be compacted by the compressive force from the test machine before the concrete cubic is ruptured, which can be regarded as a process of “crack closure”(see Fig.2)[18]. In the compressive stress-strain curves of the freeze-thaw damaged concrete, the initial parts of the ascending branches are not so steep as the following parts of these ascending branches, revealing a “crack closure”.

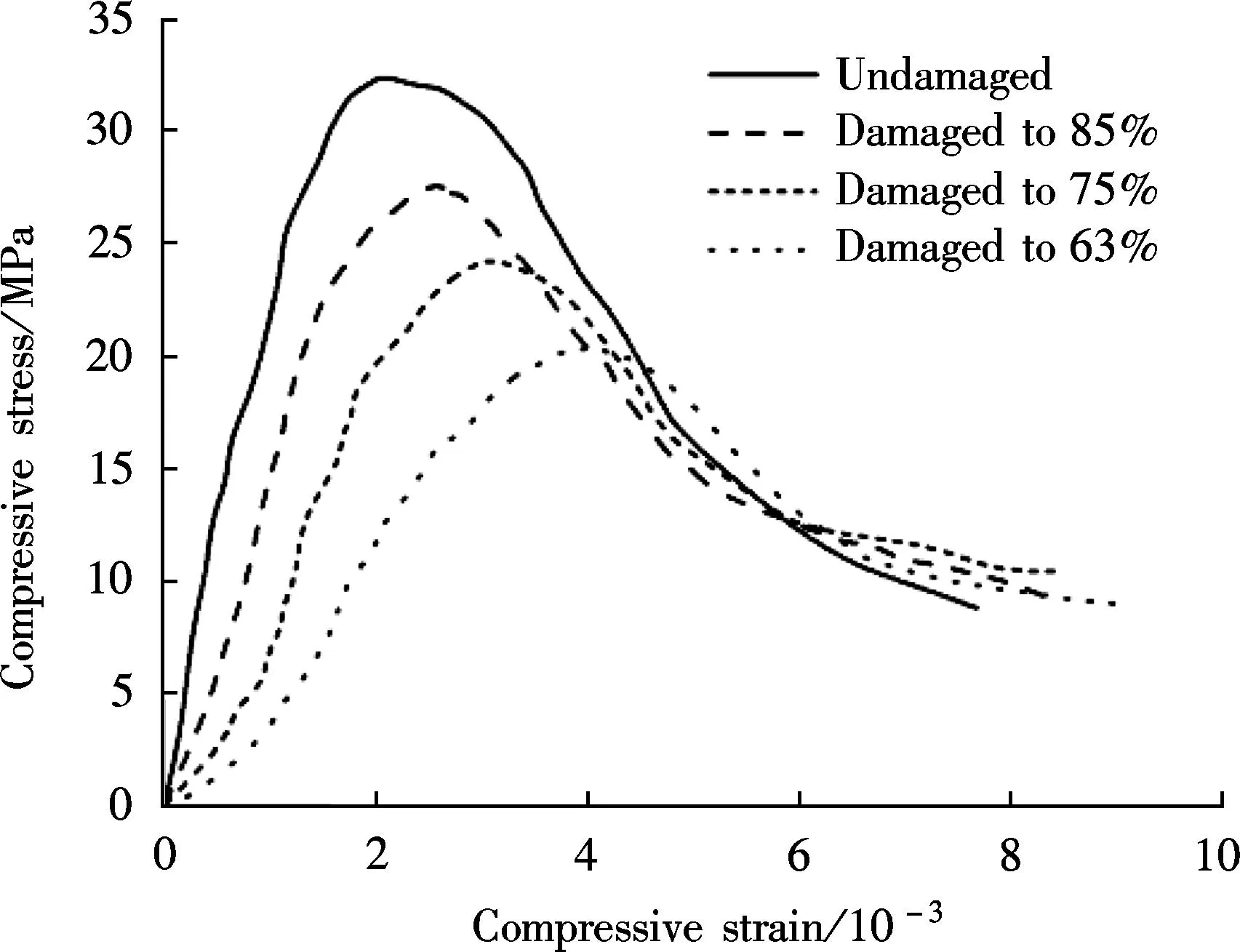
Fig.2　Stress-strain relationship under compression

Comparing the two indicators mentioned above, the compressive strength is better than the RDME theoretically. In addition, the RDME tends to recover itself if it is not measured timely, especially in high-strength concrete. However, the compressive strength varies relatively little as time goes on[19]. Last but not least, the compressive strength is a more effective indicator, which directly affects the behaviors of the freeze-thaw damaged concrete structures.

1.2　Uniaxial compression behavior after FTCs

There are lots of internal micro-cracks, mainly existing in the paste and paste-aggregate interfaces when concrete hardens even if there is not any load or environmental effect. When submerged into water, these cracks will suck water into the concrete pore system. As the temperature drops below the freezing point, water will turn into ice accompanied by a 9% volume increase, which causes tensile stress inside the concrete. If the tensile stress exceeds the tensile strength of concrete material, new internal cracks will initiate and the old ones will open wider. As FTCs are repeated, more and more water will be absorbed into the concrete during thawing, causing larger expansion and more internal cracks during the next freezing process. The load carrying area will decrease with the formation and growth of internal cracks, which leads to a decrease in the compressive strength. Since there are less micro-units to carry the load, each unit will reach its elastic limit more quickly. Hence, the compressive behavior of concrete becomes softer. The peak compressive strength and the Young’s modulus decrease, while the peak compressive strain and the ultimate compressive strain increase (see Fig.2)[18]. The damage level in Fig.2[18]is re-rated in terms of residual compressive strength.

2Theoretical Prediction Method

2.1　General considerations

Based on Refs.[15,19], the theoretical prediction is carried out by the following assumptions:

1) Plane sections before bending remain plane after bending. This assumption is proved to be true in Ref.[15].

2) The tensile strength of the concrete may be neglected. Due to freeze-thaw damage and the low tensile strength of the undamaged concrete, the freeze-thaw damaged concrete can barely carry tension.

3) The simplified stress-strain curve of the freeze-thaw damaged concrete is shown in Fig.3 and the curve is determined by

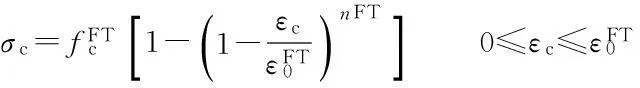
(1)

(2)

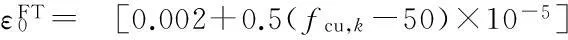
(3)

(4)

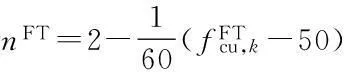
(5)

whereεcis the compressive strain in the concrete;σcis the compressive stress corresponding toεc;fcis the

Fig.3　Compressive stress-strain curve of concrete

4) The stress-strain curve for steel is perfect elastoplastic, and the ultimate strain is 0.01. Commonly, FTCs have little effect on steel, which substantiates this assumption.

2.2　Ultimate load bearing capacity

Then, based on the classic figuree of material mechanics with minor adjustments, the ultimate load bearing capacity of the freeze-thaw damaged beam can be calculated as

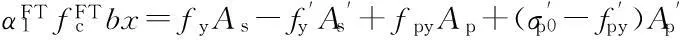
(7)

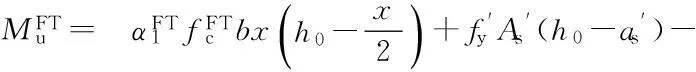
(8)

3Verification Tests

3.1　Materials

Two concrete mix designs (named type A and type B) are used. The components and mix designs for the concrete materials are described in Tab.1 and Tab.2.

Tab.1　Materials used for the concrete mix

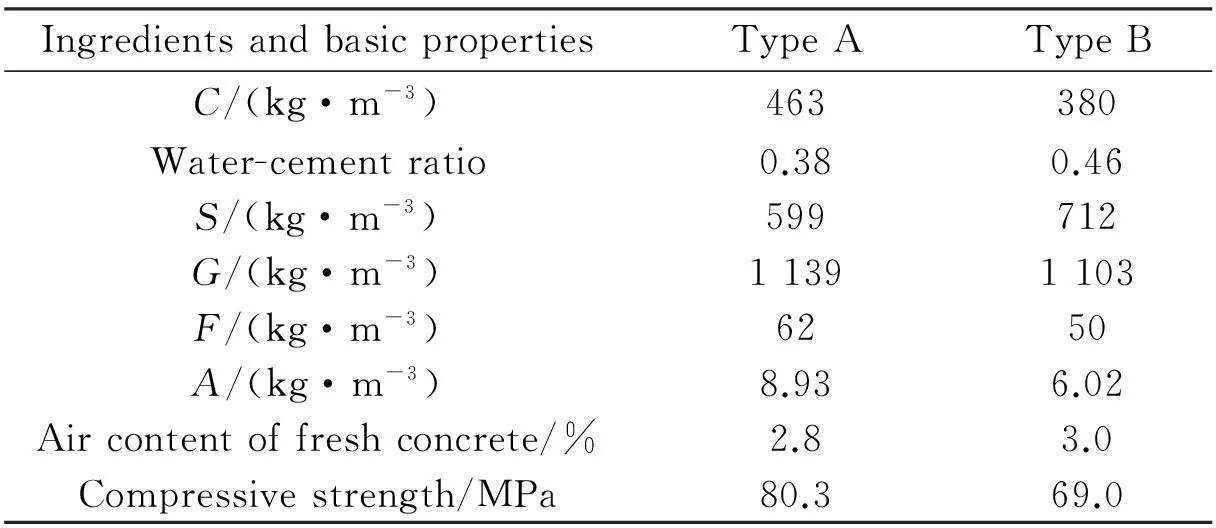
Tab.2　Concrete mix designs and basic properties

Hot-rolled ribbed steel bars (HRB335) of either 10 or 8 mm diameter were used as the longitudinal reinforcement. The stirrup was a cold-drawn wire with a diameter of 4 mm. The prestressed reinforcement was a 5 mm low-relaxation steel wire with a nominal ultimate strength of 1 570 MPa. The physical and mechanical properties of these reinforcements are shown in Tab.3.

3.2　Specimens

For each type of concrete, four kinds of specimens were prepared:

1) Twelve cubic specimens (100 mm×100 mm×100 mm), three as a group, were used to test the residual compressive strength after a specified number of FTCs.

Tab.3　Physical and mechanical properties of the reinforcements

2) Three prismatic specimens (400 mm×100 mm×100 mm) were used to test RDME during FTCs.

3) Twelve prestressed concrete beams with straight prestressed wires, three as a group, were used to test the bending response after specified number of FTCs (see Fig.4(a)).

4) Twelve prestressed concrete beams with curved prestressed wires, three as a group, were also used to test the bending response after specified number of FTCs (see Fig.4(b)).

Fig.4　Prestressed concrete beam (unit: mm). (a) With straight prestressed wires; (b) With curved prestressed wires

3.3　Program

The freeze-thaw test followed the Procedure A in ASTM C666/C666M-03[16]. In this procedure of rapid freeze-thaw in water, the temperature of the specimen was decreased from 5 to -16 ℃ and then increased from -16 to 5 ℃ over a period of 2.8 h, during which the cooling time took 2.0 h and heating took 0.8 h; i.e. 28.6 % of the time was used for thawing. Moreover, the time taken to decrease the core temperature of the specimen from 3 to -16 ℃ was about 1.7 h, and to increase it from -16 to 3 ℃ was 0.75 h. The period of transition between the freezing and thawing phases of the cycle was 5 min. All specimens were tested after 0, 75, 100, 125 FTCs, respectively.

4Results and Discussion

4.1　Compressive strength and RDME

The test results of the RDME and the residual compressive strength are shown in Fig.5. The compressive strength of type A and type B concrete decrease in a similar way. However, the RDME of type A does not decrease obviously before 100 FTCs, while the RDME of type B remains only 3% after 125 FTCs. For type A concrete, the compressive strength drops faster than the RDME. On the contrary, for type B concrete, the RDME drops faster than the compressive strength. This reinforces that the compressive strength may be a better indicator of freeze-thaw damage.

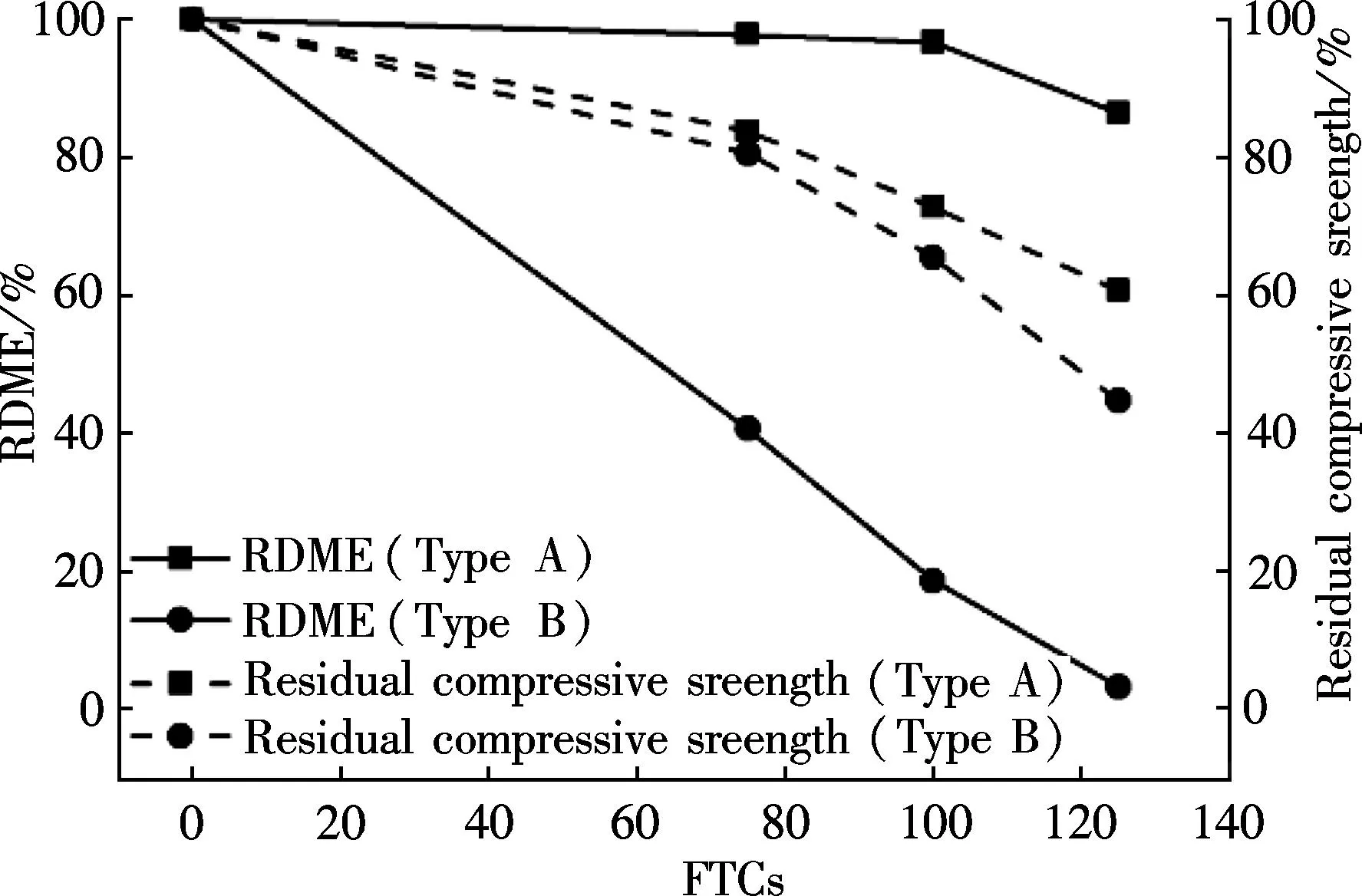
Fig.5　Test results of concrete material damaged by FTCs

4.2　Ultimate bending moment

The test results of this experiment as well as those of the experiments performed by others[21-22]are listed in Tab.4. The predicted results calculated from Eqs.(3) to (8) are shown in Tab.4.

From Tab.4, it is clear that FTCs reduce the compressive strength of concrete material, which lead to a reduction in the load bearing capacity, and this trend is sharper when the concrete damage aggravates. The layout of prestressed wire affects the load bearing capacity most when the concrete is slightly damaged; however, as damage goes on, the effect of concrete type becomes more and more dominant. Moreover, the experimental results suggest that the prestressed concrete beam with higher strength concrete and curved prestressed wire performs better under FTCs.

4.3　Comparison and discussion

The reliability of the proposed method for predicting the load bearing capacity of freeze-thaw damaged beams is shown in Fig.6. Results show that the failure load is better estimated while the concrete strength remains more than 50%. More than half of the predicted results are on the safe side (Mu,num/Mu,exp≤1), and most of the prediction errors remain less than 10%. In other words, if the margin of error is ±10%, the predicted results are reliable except for damaged beam HD2.

The overestimation of HD2 is 46%, which is larger than the FEM result in Ref.[14]. This is partly because of the bond-slip behavior which might exist in concrete

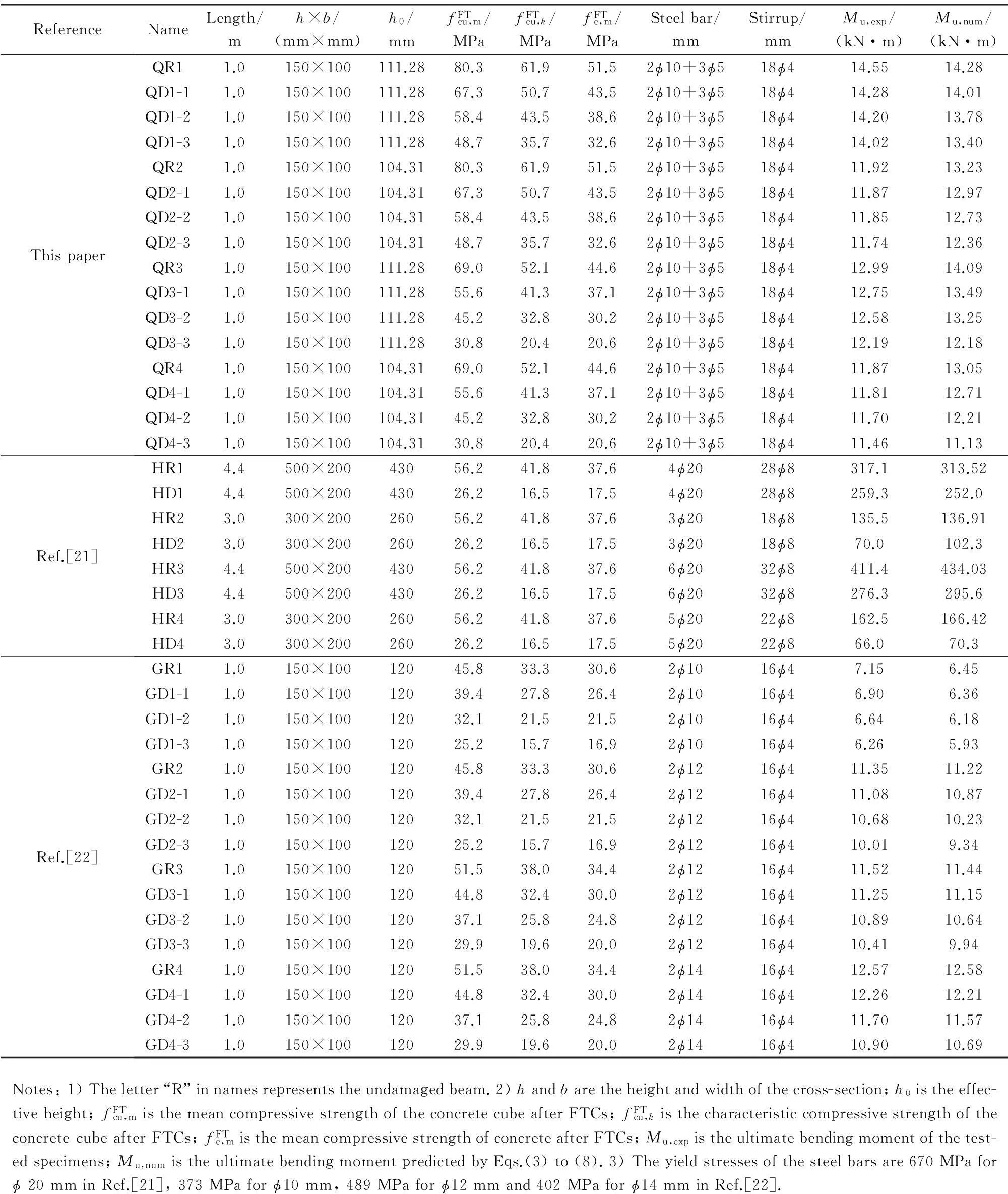
Tab.4　Summary of beam test results

beams with damage of more than 50% by FTCs. Moreover, it is reported that the freeze-thaw induced cracks of HD2 were mostly parallel to the longitudinal axis of beams, which have a decisive influence on the fracture of concrete in compression[21]. These may account for the disagreement between the theoretical and experimental results of HD2.

The load bearing capacity of freeze-thaw damaged beams can be evaluated following the method presented in this paper. The compressive stress-strain behavior of concrete blocks is the key to the load bearing capacity prediction. For most reinforced and prestressed concrete beams, the compressive behavior of concrete can be easily obtained through drilled concrete cores from the main structure or pre-casted blocks which experienced the same environmental condition as the main structure. Thereafter,

Fig.6　Comparison of results from experiments and theoretical predictions

the ultimate load bearing capacity can be calculated by Eqs. (7) and (8), which is familiar to most civil engineers. Though the prediction method is reliable for most of the concrete beams when the concrete strength loss due to FTCs is less than 50%, it is significant that bond-slip behavior will influence the accuracy of the prediction when the compressive strength loss is more than 50%. The size-effect of freeze-thaw damage was not researched thoroughly, but Ref.[23] showed that the frost-damage might significantly differ at various distances from the exposed surface. Thus, when evaluating concrete structures with larger sections, frost-damage distribution is an important factor.

5Conclusions

1) The compressive strength of concrete is proved to be a better indicator of freeze-thaw damage on concrete material than RDME.

2) Based on the characteristics of the compressive stress-strain curve of freeze-thaw damaged concrete, a theoretical method to predict the ultimate bending moment is proposed.

3) Comparisons of the predicted results with the experimental data show that the load bearing capacity of freeze-thaw damaged beams can be predicted by the proposed method.

4) Two factors, the bond-slip behavior and the frost-damage distribution, affect the prediction of the failure load, especially when the residual compressive strength is less than 50%.

References

[1]Pigeon M, Pleau R.Durabilityofconcreteincoldclimates[M]. Taylor & Francis, 1995.

[2]Fagerlund G. Modeling the service life of concrete exposed to frost[C]//InternationalConferenceonIonandMassTransportinCement-BasedMaterials. Toronto, Canada, 1999: 195-204.

[3]Cho T. Prediction of cyclic freeze-thaw damage in concrete structures based on response surface method[J].Construction&BuildingMaterials, 2007, 21(12): 2031-2040.

[4]Ueda T, Wang L, Hasan M, et al. Mesoscale simulation of influence of frost damage on mechanical properties of concrete[J].JournalofMaterialsinCivilEngineering, 2009, 21(6): 244-252.

[5]Duan A, Jin W L, Qian J R. Effect of freeze-thaw cycles on the stress-strain curves of unconfined and confined concrete[J].MaterialsandStructures, 2011, 44(7): 1309-1324.

[6]Hasan M, Ueda T, Sato Y. Stress-strain relationship of frost-damaged concrete subjected to fatigue loading[J].JournalofMaterialsinCivilEngineering, 2008, 20(1): 37-45.

[7]Li W T, Sun W, Jiang J Y. Damage of concrete experiencing flexural fatigue load and closed freeze/thaw cycles simultaneously[J].Construction&BuildingMaterials, 2011, 25(5): 2604-2610.

[8]Shang H S, Song Y P. Experimental study of strength and deformation of plain concrete under biaxial compression after freezing and thawing cycles[J].Cement&ConcreteResearch, 2006, 36(10): 1857-1864.

[9]Shang H S, Song Y P, Qin L K. Experimental study on the property of concrete after freeze-thaw cycles[J].ChinaConcreteandCementProducts, 2005, 32(2): 9-11. (in Chinese)

[10]Shang H S, Song Y P, Qin L K. Experimental study on strength and deformation of plain concrete under triaxial compression after freeze-thaw cycles[J].Building&Environment, 2008, 43(7): 1197-1204.

[11]Shang H S, Yin Q X, Song Y P, et al. Experimental study on the influence of freezing and thawing cycles on deformation features of common concrete[J].YangtzeRiver, 2006, 39(4): 60-63. (in Chinese)

[12]Sun W, Zhang Y M, Yan H D, et al. Damage and damage resistance of high strength concrete under the action of load and freeze-thaw cycles[J].Cement&ConcreteResearch, 1999, 29(9): 1519-1523.

[13]Diao B, Sun Y, Cheng S H, et al. Effects of mixed corrosion, freeze-thaw cycles, and persistent loads on behavior of reinforced concrete beams[J].JournalofColdRegionsEngineering, 2011, 25(1): 37-52.

[14]Hanjari K Z, Kettil P, Lundgren K. Modelling the structural behaviour of frost-damaged reinforced concrete structures[J].StructureandInfrastructureEngineering, 2013, 9(5): 416-431.

[15]Cao D F, Qin X C, Yuan S F. Experimental study on mechanical behaviors of prestressed concrete beams subjected to freeze-thaw cycles[J].ChinaCivilEngineeringJournal, 2013, 46(8): 38-44. (in Chinese)

[16]ASTM. ASTM C666/C666M-03 Standard test method for resistance of concrete to rapid freezing and thawing[S]. ASTM, 2008.

[17]Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB/T 50082—2009 Standard for test methods of long-term performance and durability of ordinary concrete[S]. Beijing: China Architecture & Building Press, 2009. (in Chinese)

[18]Cao D F, Fu L Z, Yang Z W, et al. Study on constitutive relations of compressed concrete subjected to action of freezing-thawing cycles[J].JournalofBuildingMaterials, 2013, 16(1): 17-23, 32. (in Chinese)

[19]Jacobsen S, Sellevold J. Self healing of high strength concrete after deterioration by freeze/thaw[J].Cement&ConcreteResearch, 1996, 26(1): 55-62.

[20]Guo Z H.Thestrengthandtheconstitutiverelationofconcrete:theoryandapplication[M]. Beijing:China Architecture & Building Press, 2004. (in Chinese)

[21]Hassanzadeh M, Fagerlund G. Residual strength of the frost-damaged reinforced concrete beams[C]//EuropeanConferenceonComputationalMechanics. Lisbon, Portugal, 2006: 366-366.

[22]Guo R Y. Experimental research on reinforced concrete bending members under freeze-thaw cycles[D]. Yangzhou: School of Civil Engineering, Yangzhou University, 2011. (in Chinese)

[23]Petersen L, Lohaus L, Polak M A. Influence of freezing-and-thawing damage on behavior of reinforced concrete elements[J].ACIMaterialsJournal, 2007, 104(4): 369-378.

doi:10.3969/j.issn.1003-7985.2015.04.016