Comparison of signal reconstruction under different transforms

Liu Jieyuan　 Wu Jiasong　 Lotfi Senhadji　 Shu Huazhong

(1Key Laboratory of Computer Network and Information Integration, Southeast University, Nanjing 210096, China)(2Institut National de la Santé et de la Recherche Médicale, U1099, Rennes 35042, France)(3 Laboratoire Traitement du Signal et de l’Image, Université de Rennes 1, Rennes 35042, France)(4 Centre de Recherche en Information Biomédicale Sino-Français, Nanjing 210096, China)



Comparison of signal reconstruction under different transforms

Liu Jieyuan1,4Wu Jiasong1,2,3,4Lotfi Senhadji2,3,4Shu Huazhong1,4

(1Key Laboratory of Computer Network and Information Integration, Southeast University, Nanjing 210096, China)(2Institut National de la Santé et de la Recherche Médicale, U1099, Rennes 35042, France)(3Laboratoire Traitement du Signal et de l’Image, Université de Rennes 1, Rennes 35042, France)(4Centre de Recherche en Information Biomédicale Sino-Français, Nanjing 210096, China)

Abstract：A new algorithm, called MagnitudeCut, to recover a signal from its phase in the transform domain, is proposed. First, the recovery problem is converted to an equivalent convex optimization problem, and then it is solved by the block coordinate descent (BCD) algorithm and the interior point algorithm. Finally, the one-dimensional and two-dimensional signal reconstructions are implemented and the reconstruction results under the Fourier transform with a Gaussian random mask (FTGM), the Cauchy wavelets transform (CWT), the Fourier transform with a binary random mask (FTBM) and the Gaussian random transform (GRT) are also comparatively analyzed. The analysis results reveal that the MagnitudeCut method can reconstruct the original signal with the phase information of different transforms; and it needs less phase information to recover the signal from the phase of the FTGM or GRT than that of FTBM or CWT under the same reconstruction error.

Key words：MagnitudeCut algorithm; signal reconstruction; different transforms; convex optimization; phase information

Received 2015-03-19．

Biographies：Liu Jieyuan (1990—), female, graduate; Shu Huazhong (1965—), male, doctor, professor, shu.list@seu.edu.cn.

Foundation items：The National Natural Science Foundation of China (No.61201344, 61271312, 11301074), the Specialized Research Fund for the Doctoral Program of Higher Education (No.20110092110023, 20120092120036), the Program for Special Talents in Six Fields of Jiangsu Province (No.DZXX-031), the Natural Science Foundation of Jiangsu Province (No.BK2012329, BK2012743), the United Creative Foundation of Jiangsu Province (No.BY2014127-11), the “333” Project (No.BRA2015288).

Citation：Liu Jieyuan, Wu Jiasong, Lotfi Senhadji, et al. Comparison of signal reconstruction under different transforms[J]．Journal of Southeast University (English Edition),2015,31(4):474-478．[doi:10.3969/j.issn.1003-7985.2015.04.008]

The problem of restoring a signal from its phase in complex transform has gained more and more attention. Generally, the phase and the magnitude of the signal in the transform domain are mutually independent, so the signal cannot be recovered only from the partial knowledge of either one. However, Hayes et al.[1]pointed out that it is possible to recover a signal from the phase-only information under certain concrete conditions. For example, exact or approximate prior information (positivity, asymmetry, sparsity, etc.) on the original signal. Many methods have been proposed to solve the above problem, including the iterative method, the statistical method, the alternating projections method[2], and the partial phase information approach[3]. Hua and Orchard[4]proposed a new image reconstruction algorithm with the simple geometrical model. Loveimi and Ahadi[5]reconstructed the speech signal via the least square error estimation and the overlap add methods. Recently, Boufounos[6]explored compressive sensing to recover sparse signals from phase information, where both the theoretical and experimental results suggest that the exact reconstruction is possible. These methods have been used in acoustical and optical hologram, electron microscopy, and X-ray crystallography. In this paper, we propose a novel approach to reconstruct signals with no assumption on the signals. Moreover, many experiments have been simulated with the phase of different matrix transforms, which are the Fourier transform with a Gaussian random mask (FTGM), the Cauchy wavelets transform (CWT), the Fourier transform with a binary random mask (FTBM), and the Gaussian random transform (GRT).

We consider the signal reconstruction problem using only the phase information because most of the signal information contained in the phase is more important than that incorporated in the magnitude with the same number of signals[1]. Inspired by the two methods reported in Refs.[7-8], the authors propose a novel magnitude recovery method called MagnitudeCut. The authors cast the original problem as a new convex optimization[9]problem, and solve it by the block coordinate descent (BCD) algorithm and the interior point algorithm. It is well known that the phase information has been utilized in many applications such as image retrieval[10]and object recognition[11]. Hence, the authors expect to recover the signal by using a small amount of phase information rather than the magnitude information.

1Phase-Only Signal Reconstruction

The original problem is figureted as

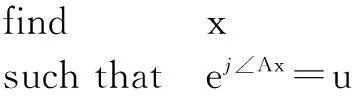
(1)

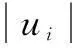
We solve (1) by separating the magnitude and phase variables. Letting Ax=diag(u)b, where b∈Rndenotes the magnitude vector, and Rnis ann-dimensional real vector space. The original problem (1) can thus be written as

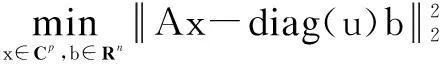
(2)

The minimization problem of figure (2) with respect to x is a standard least square problem and can be solved by setting x=A†diag(u)b, where (·)†is the pseudo-inverse operator. Therefore, figure (2) can be transformed equivalently to

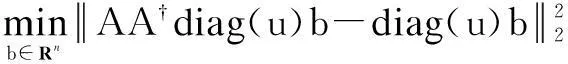
(3)

The above figure can be rewritten as

min bTMbs.t.b∈Rn

(4)

min Tr(BM)

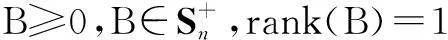
(5)

After dropping the non-convex rank constraint, we obtain the following convex relaxation:

min Tr(BM)s.t.B≥0

(6)

In order to solve the convex optimization problem (6), we use the BCD[12]to make figure (6) more conveniently solved. The proposed MagnitudeCut method is applied as the barrier version of MaxCut[13]to relax matrix B, so figure (6) becomes

min Tr(BM)-μlogdet(B)μ>0

(7)

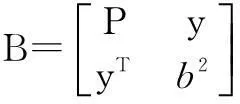
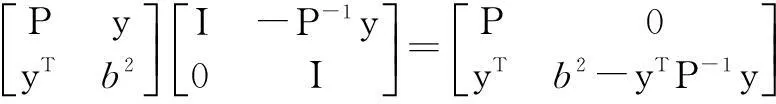
So, we obtain det(B)=det(P)det(b2-yTP-1y). Since both M and B belong to Hn, where Hnis the Hermitian matrices of dimensionn, we can figurete the complex program in Hnas the real programs[12], and obtain the following equation:

Tr(Γ(B)Γ(M))=2Tr(BM)

(8)

Tr(Γ(B)Γ(M))=Tr(2(BRe(M)))

(9)

Hence, Eq.(7) becomes

min Tr(BRe(M))-μlog{det(P)det(b2-yTP-1y)}

(10)

By using the BCD and setting Re(M)=R, figure (10) can be rewritten as

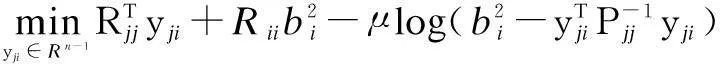
(11)

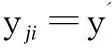
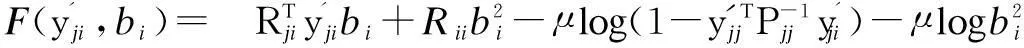
(12)

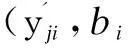
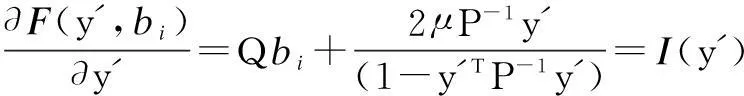
(13)

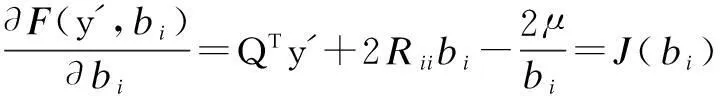
(14)

Next, we use the second-order Tayler series expansion to express Eq.(13) and Eq.(14),

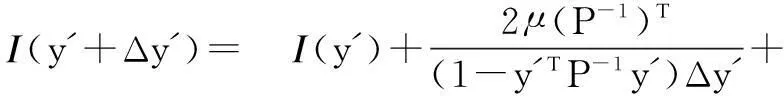
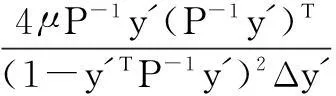
(15)

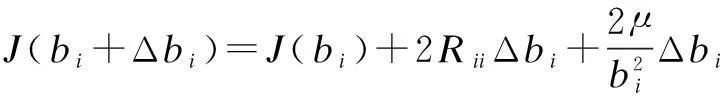
(16)

Then, we define

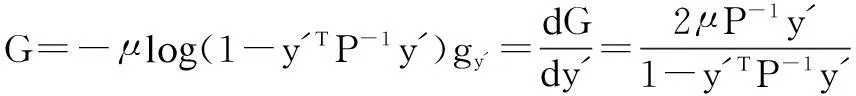
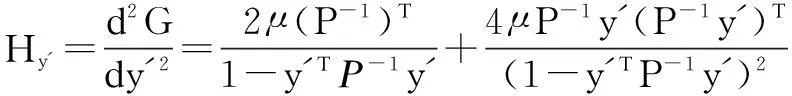
(17)

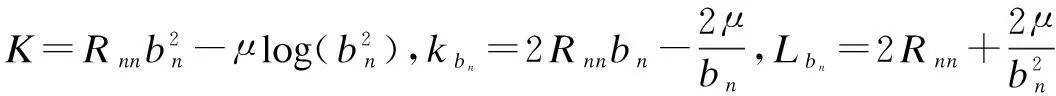
(18)

Hence, Eq.(15) and Eq.(16) are simplified as

Qbi+gy′+Hy′Δy′=0, QTy′+kbi+LbiΔbi=0

(19)

Solving Eq.(19), we have

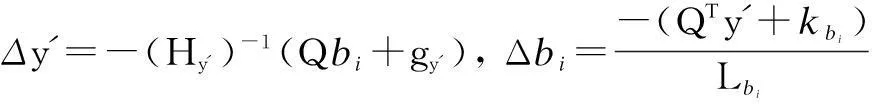
(20)

By updating Eq.(20), we obtain a better solution B as

(21)

2Simulations

The simulations are implemented by Matlab. We implement the one-dimensional and two-dimensional signal reconstructions by the MagnitudeCut algorithm and compare the signal reconstruction results by four different kinds of transform matrices: FTGM, CWT, FTBM and GRT.

2.1　One-dimensional signal

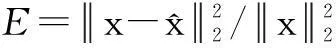
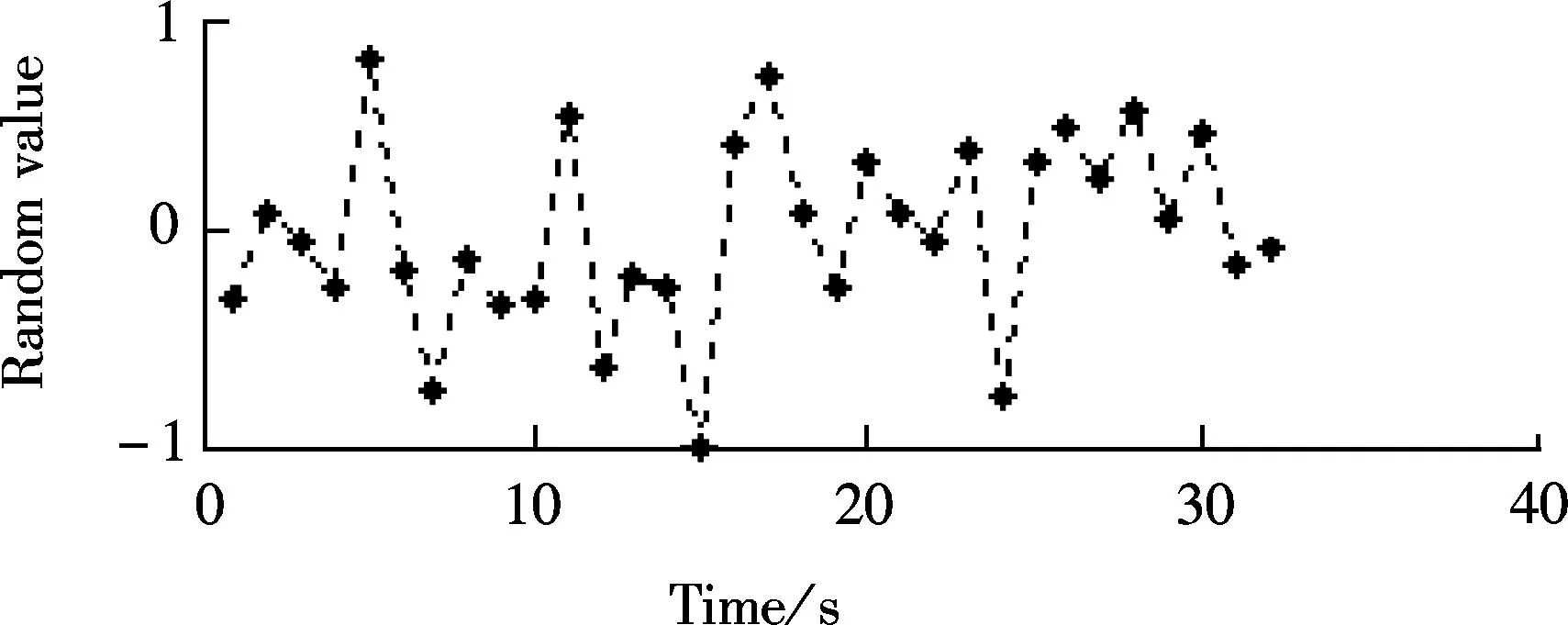
Fig.1　The original signal

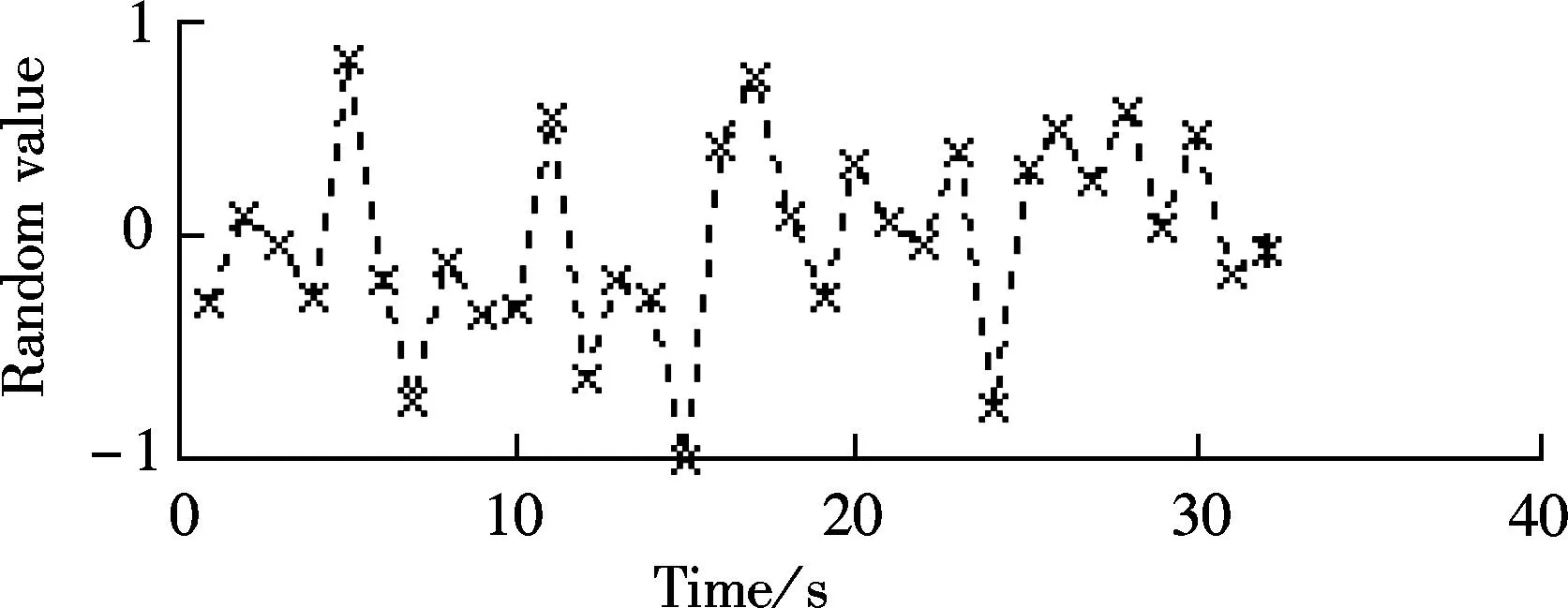
(a)

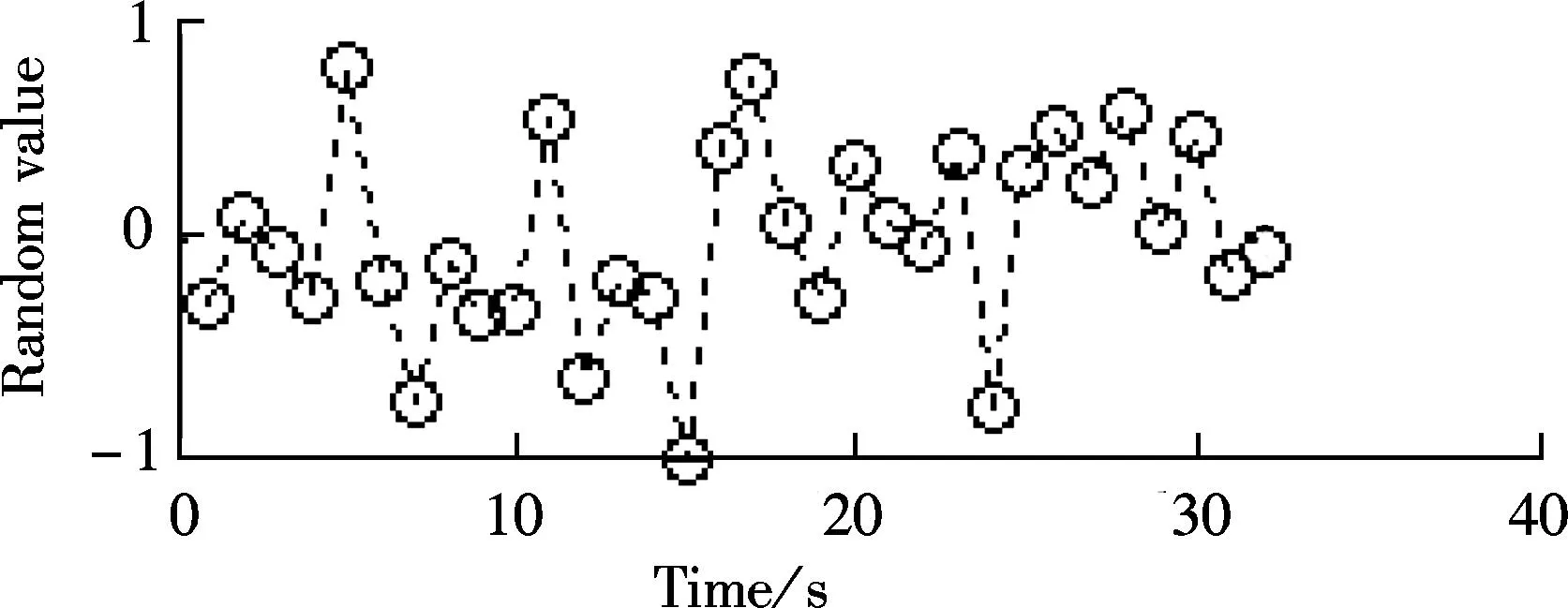
(b)

(c)

(d)Fig.2　Reconstruction results by four different transforms.

So, on the one hand, in order to reconstruct the signal from a small amount of phase information under the sameE, we need to choose FTGM or GRT. On the other hand, in the same transform domain, we can choose a set of phase information to describe a signal whose number is double the length of the original signal when a more accurate result is required. For example, in the field of info-rmation encryption, we can use less phase information under FTGM to encrypt a signal.

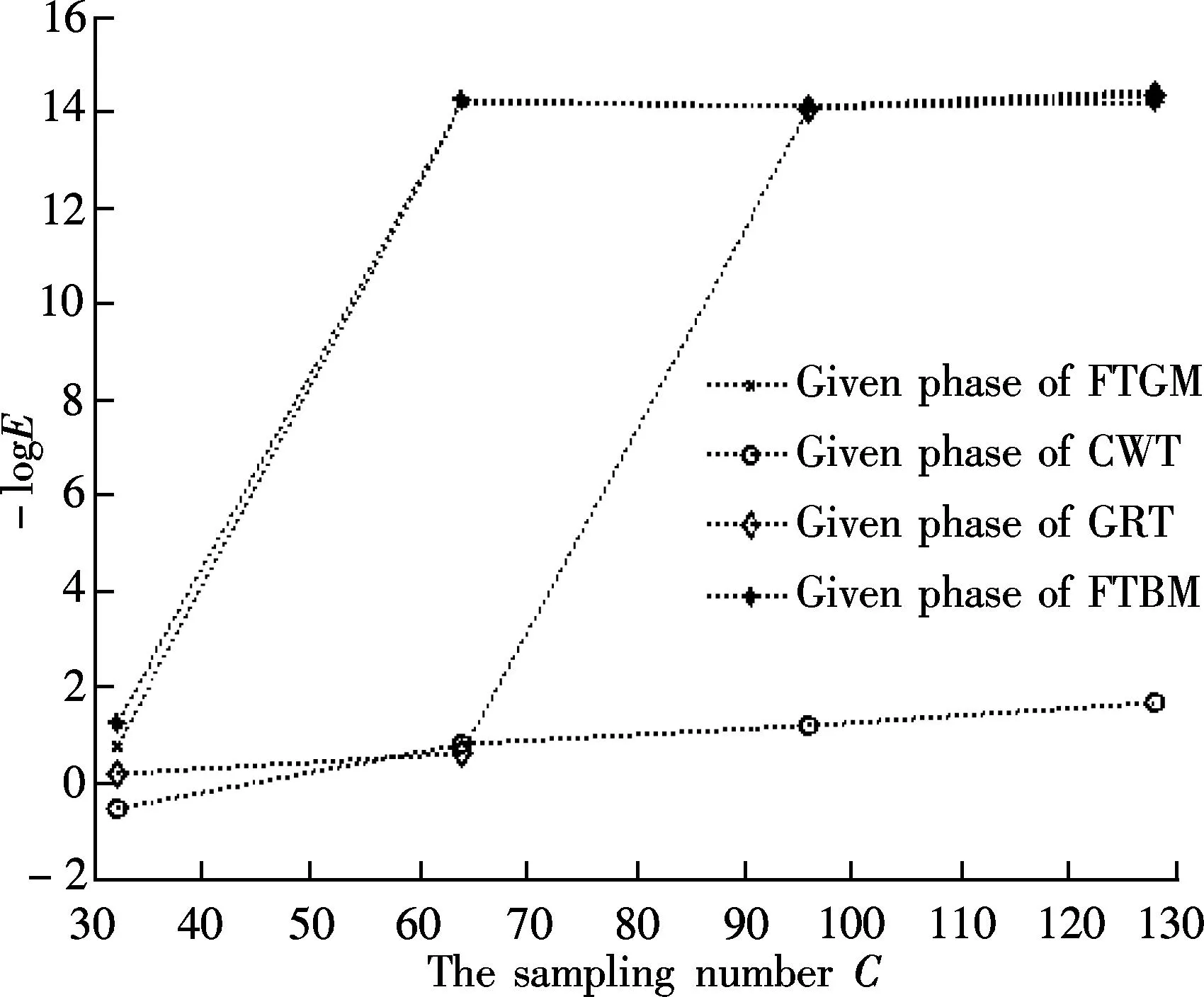
Fig.3　The reconstruction error with different transforms

2.2　Two-dimensional signal

In many cases, we need to deal with the two-dimensional signals. In this paper, three images are chosen. They are the moon’s surface, a clock and Lena, as shown in Fig.4. Supposing that the phase of each transform matrix is known, the reconstructed images withC=2 are shown in Fig.5 to Fig.7. The results reconstructed by the phase of FTGM and GRT are better than those by the phase of CWT and FTBM. Similarly, the reconstructed results withC=4 are shown in Fig.8 to Fig.10. It can be seen that with more sampling numbers, the results reconstructed by the phase of FTGM, CWT, FTBM and GRT are also better.

Fig.4　Original images. (a) Moon’s surface; (b) Clock; (c) Lena

Fig.5　Reconstructed results of the moon’s surface by four different transforms with C=2. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

Fig.6　Reconstructed results of the clock by four different transforms with C=2. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

Fig.7　Reconstructed results of Lena by four different transforms with C=2. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

Fig.8　Reconstructed results of the moon’s surface by four different transforms with C=4. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

Fig.9　Reconstructed results of the clock by four different transforms with C=4. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

Fig.10　Reconstructed results of Lena by four different transforms with C=4. (a) FTGM; (b) CWT; (c) FTBM; (d) GRT

The experimental results indicate that the two-dimensional images can also be recovered from the phase under the corresponding four transforms by the MagnitudeCut method. As a comparison, if one wants to recover a signal of sizepfrom the phase under FTGM or GRT, the sampling number should satisfyC≥2p. However, we find that good reconstruction performance can be realized withC≥3pafter observing a large number of simulation results when the transform is FTBM. In the case of CWT, we need the number of rows in the transform matrix to be equal to or larger than 4p. This not only proves the importance of phase information in the signal reconstruction process, but also explains the significance of research of the MagnitudeCut algorithm.

3Conclusion

We propose a new algorithm called MagnitudeCut to solve the problem of signal reconstruction from the phase-only information in different transform matrices, such as FTGM, CWT, FTBM and GRT. Experiments on the one-dimensional and two-dimensional signals are simulated to illustrate the feasibility of the algorithm. The merit of the proposed algorithm is that the original signal can be reconstructed with less amount of phase information than the PhaseCut algorithm. Furthermore, the results show that the phase with FTGM and GRT can obtain better results by the MagnitudeCut algorithm than the other two transforms. The phase information can preserve many more important features of a signal than the magnitude information. Therefore, if the phase information is used to describe the signal features, the requirements for the storage and the transmission bandwidth can be reduced. Since the PhaseCut algorithm is the basis of the scattering convolution networks, the proposed method shows that we can also construct a new convolution network by the phase.

References

[1]Hayes M, Lim J, Oppenheim A V. Signal reconstruction from phase or magnitude [J].IEEETransactionsonAcoustics,SpeechandSignalProcessing, 1980, 28(6):672-680.

[2]Levi A, Stark H. Signal restoration from phase by projections onto convex sets [J].JournaloftheOpticalSocietyofAmerica, 1983, 73(6):810-822.

[3]Behar J, Porat M, Zeevi Y. Image reconstruction from localized phase [J].IEEETransactionsonSignalProcessing, 1992, 40(4):736-743.

[4]Hua G, Orchard M T. Image reconstruction from the phase or magnitude of its complex wavelet transform [C]//IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing. Las Vegas, USA, 2008:3261-3264.

[5]Loveimi E, Ahadi S M. Objective evaluation of magnitude and phase only spectrum based reconstruction of the speech signal [C]//Proceedingsofthe4thInternationalSymposiumonCommunications,ControlandSignalProcessing(ISCCSP). Limassol, Cyprus, 2010:1-4.

[6]Boufounos P T. Sparse signal reconstruction from phase-only measurements [C]//Proceedingsofthe10thInternationalConferenceonSamplingTheoryandApplications. Bremen, Germany, 2013:1-5.

[7]Candes E, Strohmer T, Voroninski V. PhaseLift: Exact and stable signal recovery from magnitude measurements via convex programming [J].CommunicationsonPureandAppliedMathematics, 2013, 66(8):1241-1274.

[8]Waldspurger I, Aspremont A D, Mallat S. Phase recovery, maxcut and complex semidefinite programming [J].MathematicalProgramming, 2015, 149(1/2):47-81.

[9]Boyd S, Vandenberghe L.Convexoptimization[M]. Cambridge: Cambridge University Press, 2004.

[10]Bartolini I, Ciaccia P, Patella M. Warp: accurate retrieval of shapes using phase of Fourier descriptors and time warping distance [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005, 27(1):142-147.

[11]Shao Z, Shu H, Wu J, et al. Double color image encryption using iterative phase retrieval algorithm in quaternion gyrator domain [J].OpticsExpress, 2014, 22(5):4932-4943.

[12]Anjos M F, Lasserre J B.Handbookonsemidefinite,conicandpolynomialoptimization[M]. Dordrecht: Springer, 2011.

[13]Goemans M X, Williamson D. Approximation algorithms for MAX-3-CUT and other problems via complex semidefinite programming [C]//ProceedingsoftheThirty-ThirdAnnualACMSymposiumonTheoryofComputing. Hersonissos, Greece, 2001: 443-452.

[14]Brauner T, Endlich S, Monin A, et al. General coordinate invariance in quantum many-body systems [J].PhysicalReviewD, 2014, 90(10): 105016.

[15]Gerchberg R W, Saxton W O. A practical algorithm for the determination of phase from image and diffraction plane pictures [J].Optik, 1972, 35:237-250.

doi:10.3969/j.issn.1003-7985.2015.04.008