基于量子粒子群优化算法的结构损伤识别*

巩文龙 常军† 刘大山 康小明

(1.苏州科技学院土木工程学院，苏州 215011)(2.上海三凯建设管理咨询有限公司，上海 200070)

引言

自20世纪80年代以来，随着自然灾害频发和后期维修不善、撞击、超载等人为因素影响，已建土木结构出现不同程度损伤和功能失效的隐患，使得结构健康监测与损伤识别变得尤为重要.其中损伤识别是根据结构特征参数变化情况，诊断出结构是否损伤以及损伤位置与损伤程度［1-4］.由于损伤前后结构质量基本不变，故土木工程结构损伤的实质是结构的刚度降低，而柔度是刚度的倒数，进而柔度可以作为结构的损伤指标［5-6］.

近年来，运用柔度矩阵和智能算法的结构健康监测与损伤识别逐渐成为国内外研究的热点和难点，其中柔度矩阵以其良好的灵敏性和实用性，而备受青睐.目前大多数研究者采用柔度矩阵差、柔度差变化率、柔度曲率差等进行损伤定位［7-9］，而利用柔度灵敏度［10］和广义柔度灵敏度［11］进行损伤定量识别时存在稳定性差、识别误差较大的缺陷.遗传算法、粒子群算法等智能算法利用频率和振型构造目标函数识别结构损伤［12-13］，Zhao和Dewolf通过比较频率、振型和柔度的灵敏度，验证柔度矩阵比频率和振型更加敏感［14］，且遗传算法和粒子群算法自身存在收敛速度慢、控制参数多、容易陷入局部最优等缺点，使得智能算法识别精度还有待提高.本文结合量子粒子群优化算法和广义柔度矩阵提出了一种新的损伤识别方法，通过理论推导和数值模拟验证该方法的有效性.

1 量子粒子群优化算法(QPSO)

1995年美国社会心理学家James Kennedy和电气工程师Russell Eberhart仿效鸟群觅食群体活动，提出粒子群算法(Particle Swarm Optimization，PSO)［15］.其主要思想为每个‘粒子’代表一只觅食的鸟，都有满足解空间条件的位置和速度，以求解优化目标函数适应值为群体标准，通过不断个体思索的‘自身学习’，寻找个体最优位置或称为局部最优，通过相互间的信息交流的‘社会学习’，寻找全局最优位置，在搜索空间不断更迭，最终找到象征‘食物’的优化问题最优适应值.

粒子群算法的数学模型表述为:N维解空间存在M个相互独立粒子.第m个粒子在t时刻的位置和速度分别表示为

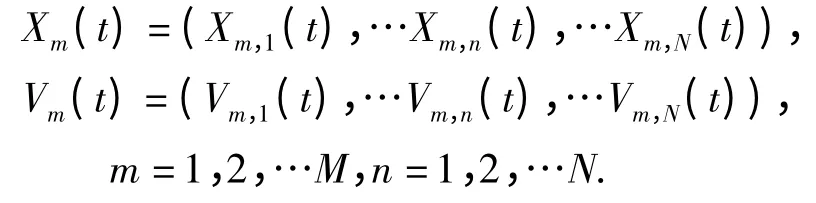
当前时刻粒子群体局部最优位置和全局最优位置分别表示为

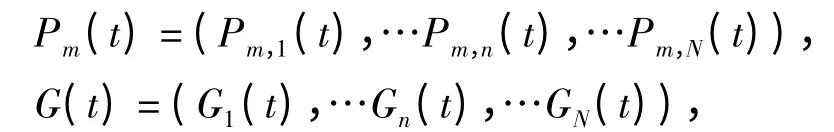
其中Pm(t)由式(1)确定，G(t)由式(2)、(3)确定.

式中f［·］表示构建的目标函数适应值

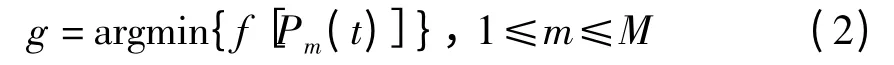
式中g为位于全局最优位置粒子对应的下标

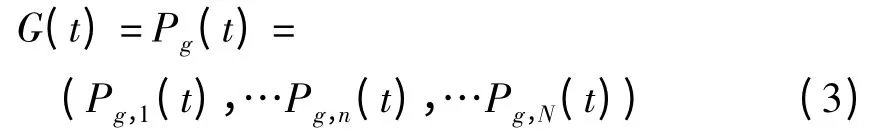
随着时间t增加，粒子群算法M个粒子的位置和速度更新为:

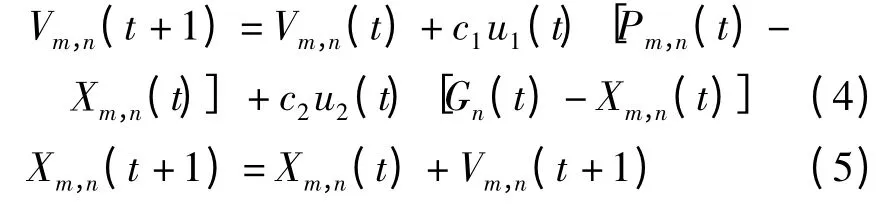
其中c1、c2分别为局部最优、全局最优加速因子，一般取(0，2)值，u1、u2为区间(0，1)均匀分布的随机数.在迭代过程中为防止粒子飞出搜索空间，需要设定Vm，n(t)、Xm，n(t)搜索上、下限.

但粒子群算法存在收敛速度慢，轨道式搜索，搜索空间有限，容易陷入局部最优等缺陷.为解决粒子群算法上述弊病，2004年Sun等人［16］提出了一种融入量子理论的改进粒子群算法——量子粒子群优化算法(Quantum-behaved Particle Swarm Optimization，QPSO)，引入的波函数和δ势阱的理念，保证了搜索空间能够覆盖整个可行空间.QPSO算法将粒子在空间的出现概率以波函数模的平方表示，保证以全概率1搜索到全局最优解，通过量子力学中粒子运动的Schrödinger动力学方程和Monte Carlo随机模拟，得到粒子在以P点为中心的δ势阱吸引下，粒子位置X的随机方程:

式中p为吸引子，L为δ势阱的特征长度，u为区间(0，1)的均匀分布的随机数，即u∈U(0，1).

随着时间t增加，QPSO算法M个粒子的位置和速度更新为:

式 中 um，n(t)，βn(t)∈U(0，1)，为收缩-扩张系数，一般取1.0～0.5线性递减，Cn(t)为t时刻第n维平均最优值，即(t)，为t时刻第m个粒子局部最优值Pm(t)的第n维数值，Gn(t)为t时刻M个粒子的全局最优值G(t)的第n维数值.令所有粒子的N维平均最优适应值为mbest，即mbest=(C1(t)，C2(t)，…CN(t)).

QPSO算法的计算流程图如图1所示。

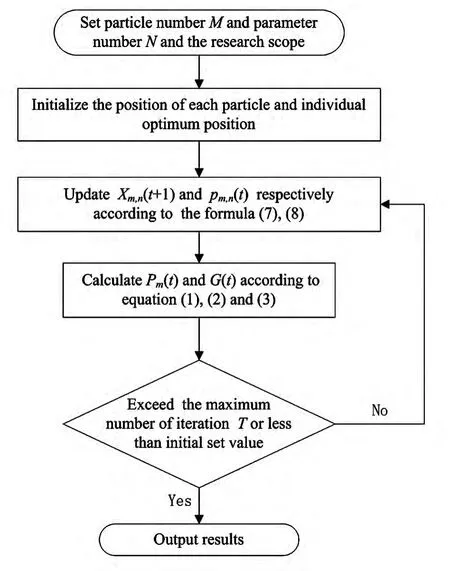
图1 量子粒子群优化算法流程图Fig.1 The flow chart of quantum-behaved particle swarm optimization algorithm

2 广义柔度矩阵基本原理

无阻尼条件下，n个自由度结构自由振动方程为:

由(9)式运动方程，得其特征方程为:

式中λ、φ分别为方程特征值，特征向量，其中λ为结构各阶固有频率的平方.

将(10)式以矩阵的形式表示为:

式中的［Ψ］=［φ1，φ2，…φn］为n阶模态振型矩阵，［Λ］=daig(λ1，λ2，…λn)为n阶对角矩阵.

由振型的质量归一化特性得:

式中的［I］为单位矩阵.

将(11)式两边同时左乘［Ψ］T得:

(12)式代入(11)式的右侧得:

(14)式两侧同时求逆，整理得:

柔度矩阵为刚度矩阵的逆矩阵，即:

由式(16)可以看出，柔度矩阵是由频率和振型构成的函数，且与频率平方的倒数成正比，随着阶次增高其模态参数对柔度矩阵的贡献越少，因此模态柔度只需前几阶模态就能很好地估计结构的柔度矩阵［17］，这也解决了实际工程监测中只能检测出结构的前几阶模态或高阶模态检测不精确的弊端.其在框架、桁架、悬臂梁等结构的使用已卓有成效［9-11］，但是对于简支梁、连续梁等结构的支座处破坏，多处损伤识别效果精度不高.

为此引入广义柔度矩阵概念［11］，其是在柔度矩阵基础上进行改进，具体函数表示为:

式中Q=0，1，2，…，当Q=0，［G］=［F］，广义柔度矩阵与一般柔度矩阵相同，当Q=1时，［G］=［Ψ］［Λ］-2［Ψ］T.

由式(17)得广义柔度矩阵中随着Q值的增大低阶模态所占的比重更大，而髙阶模态影响更小，灵敏性更高;从物理意义的角度上讲，广义柔度可以看作是单位荷载作用下各节点变形的(Q+1)次方，当结构发生损伤时，损伤前后节点变形的(Q+1)次方差值要比节点变形自身差值更加显著.为此采用以广义柔度矩阵构造目标函数识别结构损伤.

3 目标函数建立

根据式(17)建立损伤前后结构的广义柔度差为:

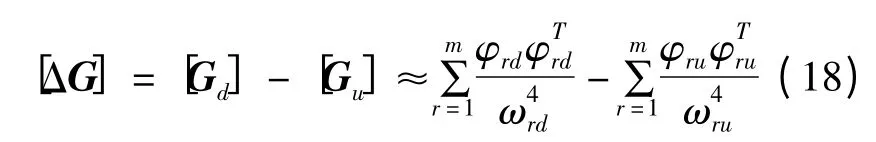
式中［Gu］、［Gd］分别表示损伤前后广义柔度矩阵，φru、φrd分别为损伤前后模态振型，ωru、ωrd分别为损伤前后模态固有频率，m为小于n的正整数.

经分析研究，文献［10-11］中采用Neumann级数或Taylor级数的柔度灵敏度和广义柔度灵敏度方法，忽略髙阶展开项，造成识别前的近似误差，这是导致其识别精度难以提高的根本.

设损伤前结构的刚度矩阵为［Ku］，第i个未损伤单元的整体刚度矩阵为损伤后结构的柔度矩阵为［Kd］，则损伤前后结构的刚度差为:

式中θi为第i个单元损伤参数，令

构造目标函数H(θ)为:

式中θ=(θ1，θ2，θ3，…θn)，原则上θ取值范围为0≤θ≤1，考虑到QPSO算法粒子的搜索最优取值范围，以及结构损伤90%时基本丧失其使用功能，调整θ取值范围为-0.1≤θ≤0.9.

4 数值模拟

如图2所示建立长5 m简支梁，将该梁划分十个单元，结构物理参数见表1.

表1 简支梁截面特性及材料属性Table 1 Sectional dimensions and material properties of simple beam

图2 简支梁模型Fig.2 Simple beam model

为验证该理论的有效性，设置如表2损伤工况，同时考虑实际模态参数识别存在误差，加入(0%，0%)、(1%，1%)、(1%，5%)、(1%，10%)四种不同噪声来反映广义柔度矩阵抗噪性，其中加噪的每个括号第一项代表在频率上加噪，第二项代表在振型上加噪.取前四阶模态，分别利用柔度灵敏度、广义柔度灵敏度、QPSO算法+广义柔度(以下分别简称为，柔度灵敏度(FS)、广义灵敏度(GFS)、QPSO+广义(QPSO+GF))三种方法识别不同工况下结构损伤，识别结果参见图3～图4及表3，其中QPSO算法的参数设置如下:粒子数为30，迭代次数为2000次.当单元损伤小于5%时，认为单元是基本完好的.

表2 损伤工况Table 2 Damage cases

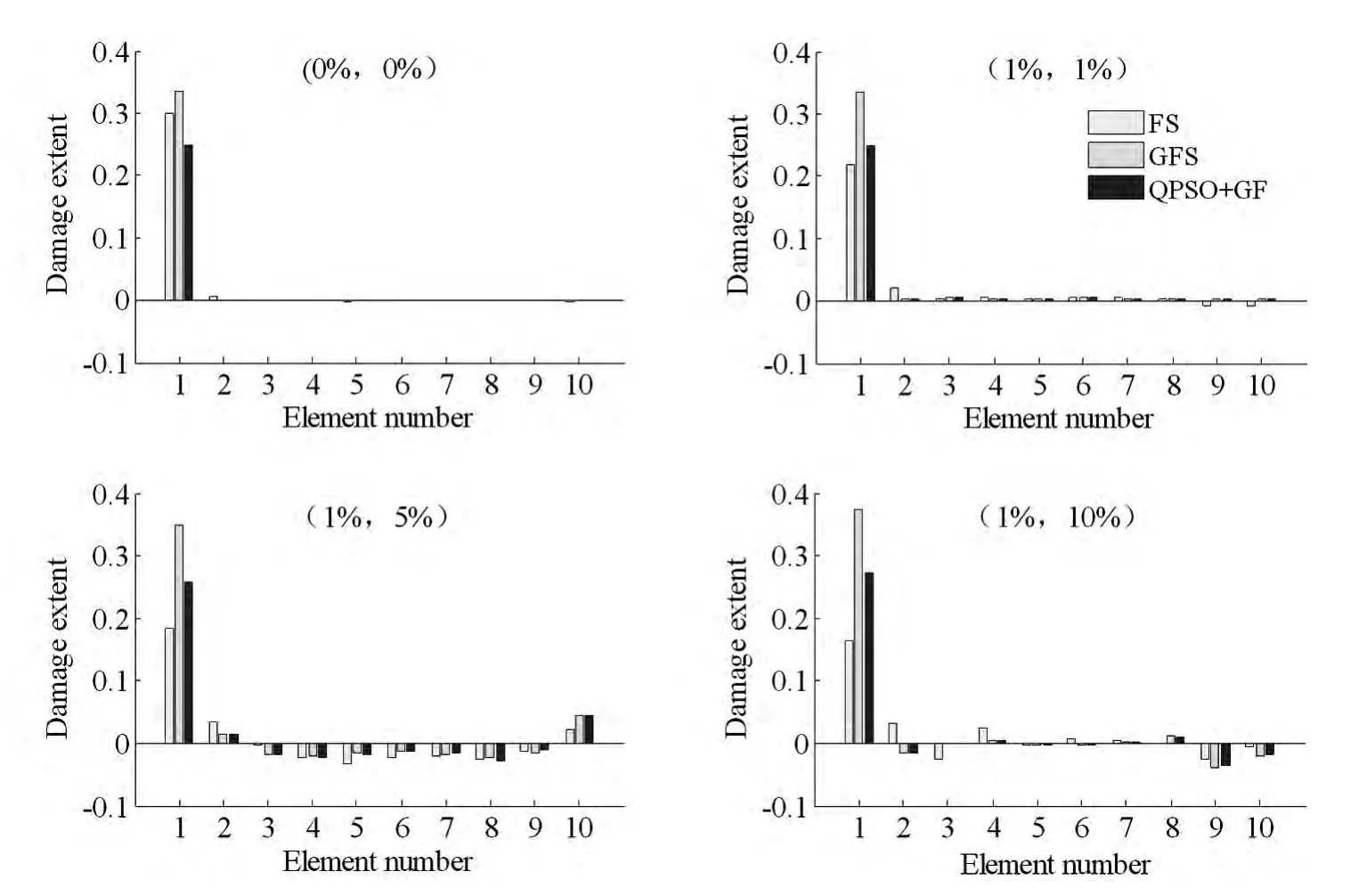
图3 工况1在不同噪声下识别结果Fig.3 Identified results of Case 1 under different noise level

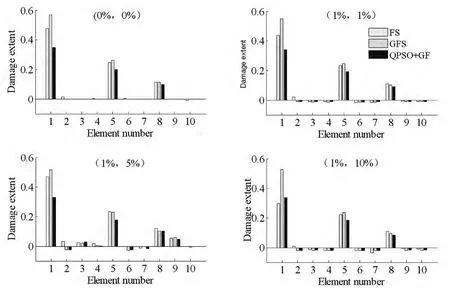
图4 工况2在不同噪声下识别结果Fig.4 Identified results of Case 2 under different noise level

表3 不同工况下三种方法识别结果Table 3 The identification results of the three distinct methods in different cases

由图2～图4和表3分析得:(1)工况一中柔度灵敏度识别结果不稳定，且误差都大于15%，广义灵敏度识别结果较为稳定，但识别误差都大于30%，QPSO+广义识别值稳定在真实值附近且最大误差为8.8591%;(2)工况二中柔度灵敏度识别支座处1单元损伤不稳定，误差不小于15%，跨中附近5、8单元识别较稳定但误差都大于10%，广义灵敏度识别1和5单元损伤较稳定但误差分别大于45%、14%，8单元小损伤识别较好且误差小于16%，QPSO+广义识别除5单元在加噪(1%，5%)识别误差10.7299%、8单元在加噪(1%，10%)识别误差16.4506%外，其他无论支座还是跨中识别误差都在10%以内.

5 结论

(1)不论单点损伤还是多点损伤，文中所提出的广义柔度差矩阵为目标函数的QPSO算法都能精确地识别出损伤位置和损伤程度.

(2)对于支座附近损伤和轻微损伤QPSO算法仍能够准确识别，解决了柔度矩阵灵敏度、广义柔度矩阵灵敏度损伤定量误差大，识别不稳定的缺陷.

(3)通过不同加噪情况仿真模拟实测模态参数的不准确性，表明QPSO算法+广义柔度具有良好的鲁棒性，QPSO算法未来在实际工程损伤检测具有广阔的应用前景.

(4)广义柔度矩阵和柔度矩阵一样，需先对振型进行质量归一化，如何处理损伤前结构模态参数未知条件下，QPSO算法识别结构损伤还有待进一步研究.同时实际测试受到各方面限制，导致测试模态不完备，有限测试信息下结构损伤的定位定量分析还有待探究.

1 Doebling W S，Farrar R C，Prime B M.A summary review of vibration-based damage identification methods.The Shock and Vibration Digest，1998，30(2):91～105

2 Fugate M L，Sohn H，Farrar C R.Unsupervised learning methods for vibration-based damage detection.In:Proceedings of the International Modal Analysis Conference-IMAC，2000，1:652-659

3 闫桂荣，段忠东，欧进萍.基于结构振动信息的损伤识别研究综述.地震工程与工程振动，2007，27(3):95～103(Yan G R，Duan Z D，Ou J P.Review on structural damage based on vibration data.Journal of Earthquake Engineering and Engineering Vibration，2007，27(3):95～103(in Chinese))

4 李学平，余志武.基于动力特性的结构损伤识别方法.动力学与控制学报，2006，4(1):84～87(Li X P，Yu Z W.Structural damage identification method based on dynamic properties.Journal of Dynamics and Control，2006，4(1):84～87(in Chinese))

5 Raghavendrachar M，Aktan A E.Flexibility by multireference impact testing for bridge diagnostics.Journal of Structural Engineering，1992，118(8):2186～2203

6 Zhang Z，Aktan A E.Application of modal flexibility and its derivatives in structural identification.Research in Nondestructive Evaluation，1998，10(1):43～61

7 Pandey A K，Biswas M.Damage detection in structures using changes in flexibility.Journal of Sound and Vibration，1994，169(1):3～17

8 孙国，顾元宪.连续梁结构损伤识别的改进柔度阵方法.工程力学，2003，20(4):50～54(Sun G，Gu Y X，Improved flexibility matrix method for damage identification of multi-span beams.Engineering Mechanics，2003，20(4):50～54(in Chinese))

9 曹晖，张新亮，李英民.利用模态柔度曲率差识别框架的损伤.振动与冲击，2007，26(6):116～120，124(Cao H，Zhang X L，Li Y M，Damage evaluation of frames by modal flexibility curvature.Journal of Vibration and Shock，2007，26(6):116～120，124(in Chinese))

10 杨秋伟，刘济科.结构损伤识别的柔度灵敏度方法.中山大学学报(自然科学版)，2010，49(1):305～308(Yang QW，Liu JK.Damage identification by the sensitivity analysis of structural flexibility.Acta Scientiarum Naturalium Universitatis Sunyatseni，2010，49(1):305～308(in Chinese))

11 李晶，吴柏生.基于广义柔度矩阵的结构损伤识别方法.吉林大学学报，2009，47(4):737～739(Li J，Wu B S.A structural damage identification method based on generalized flexibility matrix.Journal of Jilin University(Science Edition)，2009，47(4):737～739(in Chinese))

12 Perera R，Torres R.Structural damage detection via modal data with genetic algorithms.Journal of Structural Engineering，2006，132(9):1491～1501

13 陈震，朱军华，余玲.一种基于改进PSO算法的结构损伤识别方法.振动与冲击，2012，31(5):17～20(Chen Z，Zhu J H，Yu L.An improved PSO algorithm for structure damage identification.Journal of Vibration and Shock，2012，31(5):17～20(in Chinese))

14 Zhao J，DeWolf T J.Sensitivity study for vibrational parameters used in damage detection.Journal of Structural Engineering，1999，125(4):410～416

15 Kennedy J，Eberhart R C.Particle swarm optimization.In:Proceedings of IEEE International Conference on Neural Networks，1995:1942～1948

16 Sun J，Feng B，Xu WB.Particle swarm optimization with particle quantum behavior.In:2004 IEEE Congress on Evolutionary Computation，Portland:IEEE Press，2004:325～331

17 谢慧才，程林.基于柔度差曲率的简支梁损伤识别方法.汕头大学学报(自然科学版)，2007，22(3):70～75(Xie H C，Cheng L.Discussion of simply supported beam damage detection based on curvature of the flexibility difference matrix.Journal of Shantou University(Natural Science)，2007，22(3):70～75(in Chinese))