沿轴向飞行粘弹性夹层梁热弹耦合振动响应分析*
2015-03-01王金梅李映辉
王金梅 李映辉
(1.西南交通大学土木工程学院,成都 610031)(2.西南交通大学力学与工程学院,成都 610031)
引言
随着飞行器速度的提高,气动加热现象严重,因此在高速飞行结构中的局部热弹耦合振动问题备受关注[1-2].温度场的不均匀变化使结构内部出现温度梯度,较高温度梯度会引起热应变和热应力从而使结构的振动特性发生改变,热弹耦合动力学就是研究温度场和应变场耦合时弹性体的动力学行为.
关于热对结构振动的影响,一些学者用不同的方法对非耦合[3-6]和耦合[7-10]振动特性和响应进行了研究.同时,由热弹性引起的阻尼也是各种阻尼器[11-13]工作中能量损失的一个重大部分.这些问题的计算相当地复杂,在对计算精度要求不高的情况下,可以不考虑耦合项,只把热效应以等效载荷的形式作用于振动方程[14-15].在对计算精度要求高的结构设计中,热弹耦合作用不能忽略,必须同时求解热传导方程和振动方程,关于耦合求解,一些学者通过将离散的控制方程转化为模态坐标以减少求解方程的数目[4-6],并且认为沿结构长度和厚度方向温度均匀分布.然而由于热传导的速度远远小于弹性波的传播速度,采用上述方法要同时得到热弹耦合振动方程的解相当困难,需要大量的计算时间,而且可能得不到收敛解.针对这个问题,Emil[16]结合有限差分法和模态坐标转换法,推导了一种新的数值方法,分析了承受机械载荷和热载荷的梁的大幅热弹耦合振动问题.目前粘弹性夹层结构在航天航空领域也得到广泛的应用,但对于这类结构在飞行状态下的热弹耦合响应研究较少.
本文将基于Emil发展的数值方法,结合伽辽金法对承受机械载荷及热冲击载荷的轴向飞行粘弹性夹层梁的振动响应和温度分布进行研究.
1 基本方程
图1为粘弹性夹层梁几何模型,长L,宽b,上下约束层弹性模量E,厚度均为h/2,密度ρ,中间粘弹性软夹层弹性模量E',密度ρ',厚度H,粘性常数η.梁沿x方向的轴向飞行速度为v,且不考虑轴向惯性力的影响.
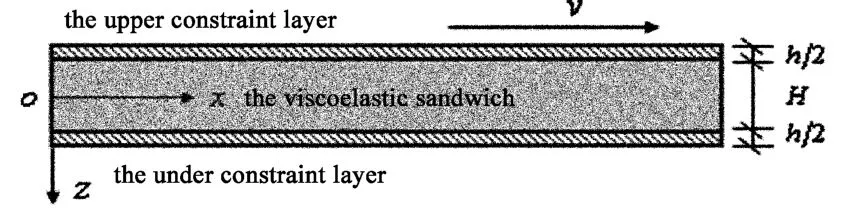
图1 梁的几何尺寸和坐标系统Fig.1 The viscoelastic sandwich beam dimensions and coordinate system
小变形情况下,考虑温度效应时,约束层和夹层的几何方程分别为

本构方程分别为

式中ΔT=T-T0,T=T(x,z,t)(假设温度在y方向均匀分布)为瞬时温度,T0为初始温度,α、α'分别为约束层和夹层材料的热膨胀系数,w=w(x,t)为梁在z方向的位移,w,(·)表示w对(·)求偏导.梁截面弯矩

式中I1、I2、I3分别为梁上中下三层对y轴的惯性矩.Mt为热力矩,定义为
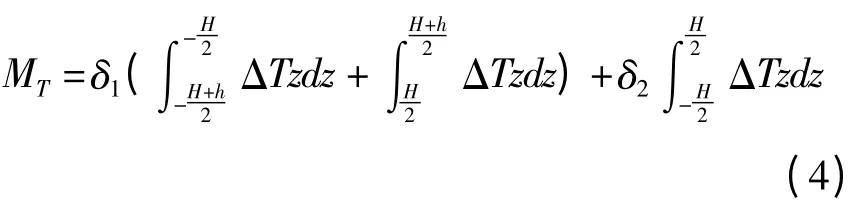
式中δ1=bαE,δ2=bα'E'.
在载荷激励F(x,t)作用下描述沿轴向飞行夹层梁的温度分布和振动问题的方程为

式(1)和(3)代入式(5)得由位移场和温度场表示的控制方程

式中,A1=EI1+EI3+E'I2,A2=ηI2,A3=A(ρh+ρ'H)/(h+H).
2 边界方程和初始条件
假设梁的下表面以及x=0和L的两端面绝热,在梁的上表面作用有一集度为Q(x,t)的热流.则热边界方程和界面方程为

式中dt为对流传热系数,t0为热流持续时间.对自由梁,边界条件为(其它边界可同样处理)
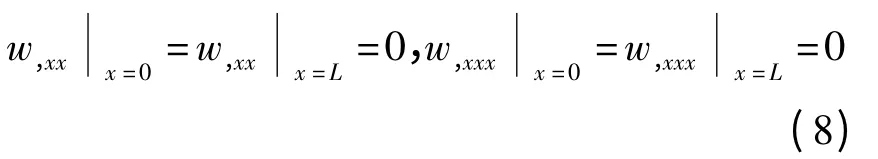
初始条件

3 数值求解方法
3.1 振动方程求解
设振动方程(6c)的位移解为

式中,wn(x)为满足边界条件的特征函数,qn(τ)为模态坐标,Nf为模态截断阶数.
将(10)代入(6c)中,两端同乘以wn(x)后对x在[0,L]上积分得

M、D、K分别定义为广义质量、阻尼、刚度矩阵,在每一时间步内的虚加荷载{F-G}可由以时间为变量的二次多项式插值得到[16]:
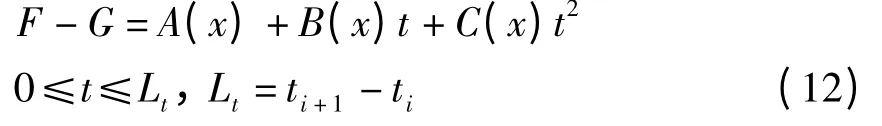
定义


式中,A、B和C是关于Fi、Gi(i=0~2)的表达式.mLt代表Lt时间间隔内的一个中间点.则式(11)可写为

式中,
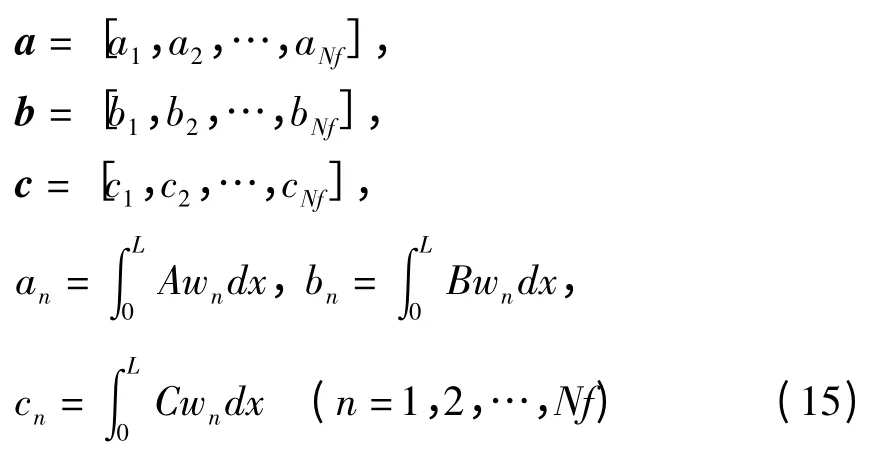
由方程(9)定义的初始条件转换为关于qn(0)和(0)的形式:
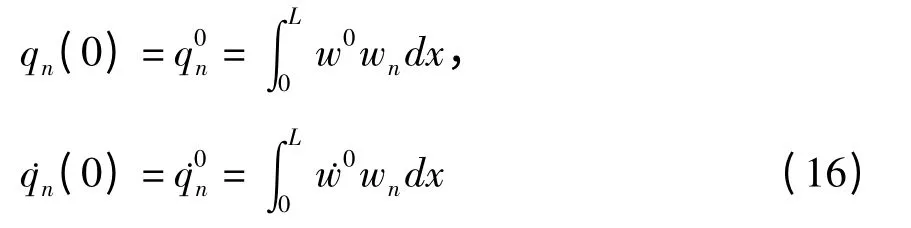
求解方程组(14)得每一时间步[ti,ti+1]内的qn(t),代入式(10)得到位移解.
3.2 热传导方程的离散和求解
用中心差分法对方程(6a,6b)进行空间离散,得到
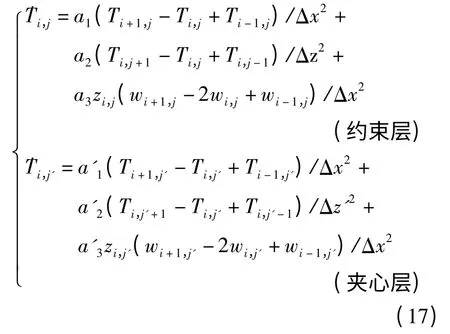
式中i=1,…,Nx,j=1,…,Nz,j'=1,…,N_z,Δx=L/(Nx-1),Δz=H/(Nz-1),Δz'=H/(N_z-1),a1=a/[1+α2ET0/ρCv],a2=a1,a3=α/[ρCv+α2ET0],a'1=a'/[1+α'2E'T0/ρ'C'v],a'2=a'1,a'3=α'/[ρ'C'v+α'2E'T0].Nx、Nz、N_z分别为沿x轴及沿z轴约束层和夹层所取离散点的数目.
初始条件和热边界的离散形式为

式中i=1,…,Nx;j=1,…,2Nz+N_z.
热力耦合的效应由系数δ1、δ2、a3确定,如果δ1=δ2=a3=0就转化为非耦合问题.
3.3 求解流程
在每一个时间段[ti,ti+1]内,进行如下迭代:
1)形成载荷向量P0、P1、P2及G0.
2)任选非零常数r1、r2计算G1=r1G0和G2=r2G0.
3)由方程(12)、(15)计算A、B和C,an、bn和cn.
4)由方程(14)和(10)计算qn(t)和w.
5)以方程(10)、(17)为基础,求解热传导问题并得到G的新值.
6)检查结果是否收敛:

其中,‖G‖为向量G的欧式范数,k+1和k分别为当前和先前的迭代次数.
如果式(19)不满足,令Gk=Gk+1,并用虚载荷向量G的新值从3)到6)重新进行迭代.如果式(19)满足,令t=ti+1为初始条件进行下一时间步的迭代.
4 数值计算与讨论
由于轴向运动和热流冲击会改变结构的振动特性,本文将使用数值仿真讨论轴向速度和热流冲击对梁振动响应的影响.数值计算中夹层梁的几何参数和材料参数如表1和表2.

表1 粘弹性夹层梁几何参数Table 1 Geometry size of viscoealstic sandwich beam
设作用于梁上表面的热脉冲沿梁长度以正弦分布,其幅值随时间衰减,关系如下:

式中,Q0=106W/m2,t0=0.01s.
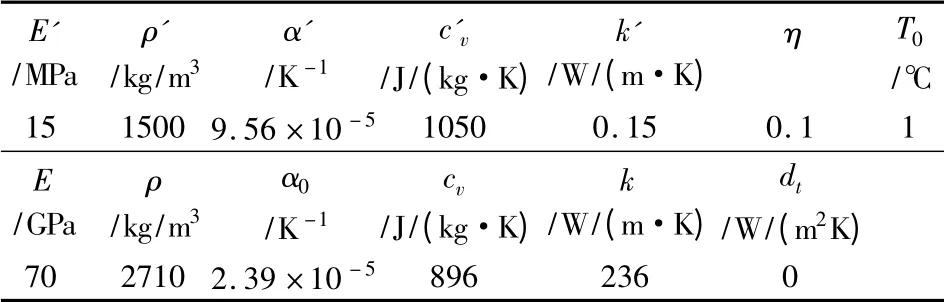
表2 粘弹性夹层梁材料参数Table 2 Material parameters of viscoelastic sandwich beam
作用于梁上的外激励为F=F0sin(ωt).计算中,取满足边界条件的特征函数wn(x)=chβnx+cosβnx-(shβnx+sinβnx)(chβnL-cosβnL)/(shβnL-sinβnL),其中,chβnL cosβnL-1=0.其余相关参数取值:Nx=61,Nz=5,N_z=11,Nf=5,r1=1.5,r2=0.8,m=0.5,数值结果及讨论如下.
4.1 速度的影响
轴向运动会诱发结构的不稳定振动和颤振失稳[7].基于文[7]的方法得到梁的频率随时间的变化曲线如图2.在0≤v<365m/s时,夹层梁的频率为实数,虚部为零,为稳定振动,且随着速度的增大,振动频率随之减小;当365≤v≤521m/s(发散速度区间)时,一阶频率实部等于零,其虚部呈正负两个分支,这时一阶模态发散失稳,最小发散速度(v=365m/s)为临界速度;当571≤v≤700m/s时,一阶和二阶频率实部相等,虚部呈正负两个分支,称为耦合颤振.

图2 频率随轴向速度的变化(a)频率实部;(b)频率虚部Fig.2 The variation of the frequency with the axially speed(a)The real part of the frequency;(b)The imaginary part of the frequency
图3为稳态振动时,梁左端点的位移响应和上接触面中点温度变化曲线,计算中F0=100N,ω=100rad/s.可见,临界速度之前,随着轴向运动速度的增大,梁的横向振动位移也随之增大;而温度随速度的改变基本没有变化.
图4和图5分别给出了发散速度及一阶和二阶耦合颤振时速度下梁左端点的位移响应和上接触面中点的温度变化曲线,计算中F0=100N,ω=100rad/s.可见,这时结构的运动失稳发散,温度也随之发散.
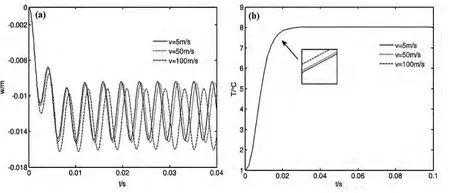
图3 稳态速度对位移场和温场的影响(a)响应(x=0);(b)上接触面中点的温度Fig.3 The influence of the stable speed on the displacement and temperature fields(a)Time history of response;(b)The temperature at the upper contact face of the beam's middle cross section

图4 发散速度对位移场和温场的影响(a)响应(x=0);(b)上接触面中点温度Fig.4 The influence of divergence speed on the displacement and mperature fields(a)Time history of response;(b)The temperature at the upper contact face of the beam's middle cross section

图5 颤振时速度对位移场和温场的影响(a)响应(x=0);(b)上接触面中点温度Fig.5 The influence of flutter speed on the displacement and mperature fields(a)Time history of response;(b)The temperature at the upper contact face of the beam's middle cross section
4.2 热作用影响
图6为外激励频率接近一阶固有频率时,有无热流冲击两种情况下夹层梁的强迫振动响应,其中F0=100N,ω=1500rad/s,v=5m/s.当没有热流冲击时,由于激振频率接近一阶固有频率,梁的振动出现拍现象.当有短暂热流脉冲时,由于温度的连续传播,以及沿梁的横截面垂直于y轴的方向不均匀的温度分布引起的弯矩,导致梁的平衡状态随时间而改变,振动围绕另一新的平衡状态进行,且振幅量级明显增大.与无热流情况相比,热流冲击时段,出现了更剧烈的跳动现象.
图7为梁在x=0点处不同脉冲时间下的响应,其中F0=100N,ω=100rad/s,v=5m/s,Q0t0=104Ws/m2为常数,表示热流总量为定值.可见,短脉冲引起更大幅值的振动,即在一个固定的短时期内,有更多能量传输给了梁.

图6 热冲击对振动响应的影响(a)响应曲线(x=0);(b)相图(1)Q0=0;(2)Q0=106W/m2,t0=0.01sFig.6 The influence of heat flow on the beam's response(a)Time history of the beam's response;(b)Phase plot

图7 热脉冲参数对梁振动响应的影响Fig.7 The influence of the heat pulse parameters on the beam's response

图8 速度对温度场的影响Fig.8 The influence of axially speed on the temperature field

图9 梁纵截面温度分布Fig.9 Distribution of the temperature in the longitudinal section
图8给出了热冲击时间t0=0.01s时梁上中点的温度随时间的变化曲线,其中F0=100N,ω=100rad/s,v=5m/s.由于约束层金属材料传热性能好,夹层粘性材料一般为热的不良导体并且散热条件较差,导致温度在夹层内的传播远小于约束层,能量蓄积在梁内,引起较大的温度梯度,且一段时间后,由于阻尼层对温度传播的阻碍,约束层的温度达到一个平衡状态,并保持一段较长时间.不同时刻下,梁上纵截面温度分布如图9(为观察更清晰,图中仅截取了从梁上表面开始的部分梁厚度).
5 结论
在考虑热弹耦合的情况下,研究了简谐外激励载荷与其上表面有短暂热流作用下轴向运动粘弹性夹层梁的振动.结果表明:
(1)在稳态振动阶段,随着轴向速度的增大梁的振幅增大,轴向运动对位移场影响较大,对温场影响较小;过大的轴向运动会诱发结构振动失稳.
(2)由于约束层和夹层传热的差异性,导致梁沿厚度方向上产生较大的温度梯度,从而使梁内产生应力,改变了梁的动力学行为.同时,短暂热流会引起梁的振动位移大幅增大.
1 杨炳渊,史晓鸣,梁强.高超声速有翼导弹多场耦合动力学的研究和进展.强度与环境,2008,35(6):55~62(Yang B Y,Shi X M,Liang Q.Investigation and development of the multi-physics coupling dynamics on the hypersonic winged missiles.Structure&Environment Engineering,2008,35(6):55~62(in Chinese))
2 范绪箕.高速飞行器热结构分析与应用.北京:国防工业出版社,2009(Fan X J.Thermal structure analysis and applications of high-speed vehicles.Beijing:National Defense Industry Press,2009(in Chinese))
3 Xue D Y,Mei C.Finite element nonlinear panel flutter with arbitrary temperatures in supersonic flow.American Institute of Aeronautics and Astronautics,1993,31(1):154~162
4 Dhainaut JM,Duan B,Mei C,Spottswood C SM,Wolfe H.Non-linear response of composite panels to random excitations at elevated temperatures.In:Proceedings of Seventh International Conference on Recent Advances in Structural Dynamics,2000,2:769~784
5 Zhou R C,Xue D Y,Mei C.Finite element time domain modal formulation for nonlinear flutter of composite panels.American Institute of Aeronautics and Astronautics,1994,32(10):2044~2052
6 Shi Y,Lee R Y Y,Mei C.Thermal post buckling of composite plates using the finite element modal coordinate method.Journal of Thermal Stresses,1999,22(6):595~614
7 Guo X X,Wang Zh M,Wang Y,Zhou Y F.Analysis of the coupled thermoelastic vibration for axially moving beam.Journal of Sound and Vibration,2009,325:597~608
8 Trajkovski D,Cukic R.A coupled problem of thermoelastic vibrations of a circular plate with exact boundary conditions.Mechanics Research Communications,1999,26:217~224
9 Karagiozova D,Manoach E.Coupling effects in an elasticplastic beam subjected to heat impact.Nuclear Engineering and Design,1992,135:267~276
10 李智勇,刘锦阳,洪嘉振.作平面运动的二维平面板的热耦合动力学问题.动力学与控制学报,2006,4(2):114~121(Li Z Y,Liu J Y,Hong J Z.Coupled thermoelastic dynamics of a two-dimensional plate undergoing planar motion.Journal of Dynamics and Control,2006,4(2):114~121(in Chinese))
11 Nayfeh A,Faris W.Dynamic behavior of circular structural elements under thermal loading.In:44th AIAA/ASME/ASCE/AHS Structures,Structural Dynamics,and Materials Conference,Virginia,2003
12 Arafat H,Faris W,Nayfeh A.Vibrations and buckling of annular and circular plates subjected to a thermal load.In:44th AIAA/ASME/ASCE/AHSStructures,Structural Dynamics,and Materials Conference,Virginia,2003
13 Sun Y X,Fang D N,Soh A K.Thermoelastic damping in micro-beam resonators.International Journal of Solids and Structures,2006,43(10):3213~3229
14 史晓鸣,杨炳渊.瞬态加热环境下变厚度板温度场及热模态分析.计算机辅助工程,2006,15(s):15~18(Shi X M,Yang B Y.Temperature field and mode analysis of flat plate with thermal environment of transient heating.Computer Aided Engineering,2006,15(s):15~18(in Chinese))
15 王宏宏,陈怀海,崔旭利,等.热效应对导弹翼面固有振动特性的影响.振动、测试与诊断,2010,30(3):275~279(Wang H H,Chen H H,Cui X L et al.Thermal effect on the natural vibration characteristics of the missile wing surface.Journal of Vibration,Measurement&Diagnosis,2010,30(3):275~279(in Chinese))
16 Manoach E,Ribeiro P.Coupled,thermoelastic,large amplitude vibrations of Timoshenko beams.International Journal of Mechanical Sciences,2004,46:1589~1606
