允许CAT 题目检查的区块题目袋方法*

林 喆 陈 平 辛 涛 ,

(1北京师范大学发展心理研究所, 北京 100875) (2中国基础教育质量监测协同创新中心, 北京 100875)

1 引言

计算机化自适应测验(

Computerized Adaptive Testing

, CAT)克服了传统测验存在的一些局限, 不仅能够为被试选择与其能力相匹配的测验, 比较这些被试的能力水平, 还能用更少的题目达到相同的估计精度(Weiss, 1982)。因此, 很多大型评价项目(比如, 美国医生护士资格考试 NCLEX、美国商学院研究生入学考试 GMAT和美国军事服役职业能力测验倾向成套测验 ASVAB)均采用了 CAT的形式(陈平, 张佳慧, 辛涛, 2013)。

题目检查是传统测验非常重要的组成部分。在传统的纸笔测验中, 被试可以在测验的过程中随时回看检查, 如果出现漏答、笔误、曲解题意等情况,可以及时修改作答(McMorris, 1991); 被试还可以采取跳过题目等合理的答题策略来提高测验综合表现(Vispoel, Hendrickson, & Bleiler, 2000)。题目检查已经成为被试的一种习惯和默许的权利。然而,目前绝大多数的 CAT测验不允许被试返回检查。测验开发者为了保证选题策略的精准定位、能力估计的精度、某些作弊策略的规避、时间效率以及题库安全性等问题不允许被试进行题目检查(Wise,1996)。因此, 允许 CAT题目检查成了传统纸笔测验向CAT发展过程中需要解决的一个关键问题。

在 CAT中提供题目检查的功能是有必要的。不允许题目检查使被试无法采用纸笔测验中常用的答题策略, 会额外增加紧张和焦虑等负面因素,导致被试出现本不应该出现的错误, 最终影响被试真实能力的估计(Lunz, Bergstrom, & Wright, 1992;Wise, 1996; Vispoel, 1998; Vispoel et al., 2000;Vispoel, Clough, & Bleiler, 2005)。一方面, 不允许题目检查使CAT的效度受到测验无关因素的影响,阻碍纸笔测验向CAT的转化, 影响CAT在实际中的应用(Stocking, 1997)。另一方面, 被试也希望能够检查题目, 并通过检查获得更高的分数(Waddell& Blankenship, 1994; Wise, 1996)。如果题目修改是源于被试自身的认知加工, 那么被试应当获得题目检查和修改的机会。这样才能使他们的能力得到真正的展示, 并且更加准确估计他们的真实能力(Benjamin, Cavell, & Shallenberger, 1987; McMorris,1991)。Wise, Finney, Enders, Freeman和 Severance(1999)认为如果允许题目检查可以排除或减少其对CAT估计精度的影响, 那么允许题目检查对被试和测验开发者来说都很有意义。因此, 允许CAT题目检查是一个值得研究的问题。

1.1 允许CAT题目检查对能力估计精度的影响

允许 CAT题目检查引起的一个主要问题是会降低能力估计的精度。在CAT中, 选题策略大多是通过最优化某种特定的指标来选择最适合当前能力估计值的题目。当被试对题目进行修改后, 被试的一系列能力估计值就会发生变化, 已经不同于选题策略所依据的能力估计值。因此, 选题策略选出的一系列“最优”题目对题目修改后的能力估计值来说并非最优。换句话说, 题目修改导致选题策略的不精确定位, 造成题目信息量减少, 增大了能力估计的误差, 降低了估计的精度(Lord, 1983)。

在 CAT执行过程中, 完全精准的选题定位是不可能实现的, 因为初始几个题目总是根据先验的能力值或不精确的能力估计值来选择。所以, 探究允许题目检查对能力估计精度的影响也变得更加复杂。一些研究表明允许题目检查的 CAT较传统CAT会有更大的误差 (Bowles & Pommerich, 2001;Wise, 1996; Olea, Revuelta, Ximénez, & Abad,2000)。尽管研究者研发了不同方法来实现允许题目检查的CAT, 但仍然无法避免能力估计精度的降低, 只能保证能力估计精度的降低在相对合理的范围内(Stocking,1997; Olea et al., 2000; Vispoel, 1998;Vispoel et al., 2000; Papanastasiou & Reckase, 2007;陈平, 丁树良, 2008; Han, 2013)。

1.2 允许CAT题目检查对测验公平性的影响

允许 CAT题目检查引起的另一个主要问题是会产生作弊策略, 如 Wainer策略(Wainer, 1993)和Kingsbury策略(Kingsbury, 1996), 它们会严重影响测验的效度和测验公平性。

Wainer策略是由 Wainer (1993)提出的一种操纵 CAT选题的作弊策略：被试在最初的作答过程中故意答错每一个题目, “操纵”CAT为其选择容易的题目, 在答完所有题目后, 返回检查并尽全力作答。如果该被试全部答对这些简单题目, 就会造成能力估计的正向偏差, 获得极高的能力估计值。Stocking (1997)的研究表明Wainer策略不仅会使被试的能力估计值产生较大的误差, 还会使低、中能力的被试从这种不精确的估计中获益。他还指出Wainer策略极大地影响了测验的公平性, 也让CAT的分数解释毫无意义。

Kingsbury (Kingsbury, 1996)作弊策略是另一种常见的作弊策略。当被试在某种程度上了解了每个题目难度都依赖于前一个题目的作答结果, 他们可以通过感知当前题目与前一个题目的难度变化来获得前一个题目是否作答正确的线索, 从而纠正之前答案。通过这个策略, 被试可能答对自身能力本无法答对的题目, 从而影响测验的公平性和效度。

1.3 允许CAT题目检查的已有方法

为了防止上述的两个主要问题, 一些研究者从不同角度提出了允许 CAT题目检查的方法。从限制修改的角度, Stocking (1997)提出了连续区块方法(Successive Block Method)。这种方法是在测验过程中人为设置一串连续的区块, 每个区块都分配合理的题目数量和时间, 被试可以在区块内进行题目检查和修改, 直到时间用尽或主动跳入下一个区块。当进入下一个区块后, 被试就无法再对先前区块内的题目进行修改。这种方法可以有效应对Wainer策略, 因为被试无法通过答错所有题目来操纵 CAT的选题。研究结果发现只要每个区块内的题目数量保持在较少的范围内, 被试的能力估计精度就不会显著降低。实证的研究也发现连续区块方法不仅能够有效应对Wainer策略与Kingsbury策略,同时能力估计精度的减少也在合理的范围内(Vispoel, Rocklin, Wang, & Bleiler, 1999; Vispoel et al., 2000, 2005)。

近年来, Han (2013)针对连续区块方法的不足提出了题目袋方法(Item Pocket Method)。Han认为连续区块方法是一种受限制的允许题目检查。一方面, 被试无法像纸笔测验那样随时跳过某个题目,而且只能检查并修改当前区块内的题目, 一旦跳过区块就无法检查之前的题目。另一方面, 连续区块方法为了保证能力估计精度, 往往需要设置大量的区块, 而每个区块包含少量的题目(Stocking, 1997;Vispoel et al., 1999)。这种设置不仅加剧了检查的限制, 还增加了被试对于时间决策的负荷, 也为测验开发者如何分配区块时间带来额外的负担。基于上述的不足, Han提出了题目袋方法。该方法是在测验中加入一个固定容量的题目袋作为缓存。被试可以把之后想要检查的题目或想暂时跳过的题目放入题目袋中供其随时检查和修改。当题目袋满时,被试需要替换题目袋中的某一题目或选择放弃放入, 被替换的题目必需完成作答且无法再修改。当达到终止规则后, 被试需要答完题目袋中的题目,这些题目也会纳入最终的能力估计当中, 不答则视为错误作答。这种方法的优点在于放入题目袋的题目不参与当前能力的估计, 保证整个过程中选题策略均是基于最终作答估计的能力值, 保证了选题的精确性。此外, 它给被试更充分的自主性, 被试可以在CAT过程中随时修改和替换题目袋中的题目,也可以跳过某个题目, 从而更加符合纸笔测验的作答习惯。Han (2013)的研究结果发现, 当题目袋容量较小时, 题目袋方法的估计精度与无修改条件下的估计精度差异不大。而且题目袋方法可以有效地防止Wainer策略, 而且对Kingsbury策略天然地免疫, 因为题目的选择与题目袋中的项目无关, 两者之间不存在任何联系。

此外, 还有一些研究者从能力估计、模型、选题策略等视角出发来实现 CAT题目检查。Bowles和Pommerich (2001)认为当题目修改后, 极大信息量选题策略的定位是不准确的, 但可以采用特定信息量的选题策略(Specific Information Item Selection, SIIS), 这种选题方法通过为当前能力估计值选择一个特定信息量而不是极大信息量的题目, 从而减少了作答修改对选题定位产生的影响。Papanastasiou和Reckase (2007)提出题目重排序的方法, 在估计最终能力时有选择地跳过一些不匹配的题目, 防止这些不匹配的题目对能力估计造成偏差, 从而提高能力估计精度。陈平和丁树良(2008)通过建立新的评分模型来“修复”能力估计的精度和偏差, 同时能有效地应对 Wainer策略。van der Linden, Jeon和Ferrara (2011)基于“被试的能力越高,初始作答的正确率越高, 并且将错误答案修改为正确的概率也越高”的假设, 提出一个两阶段的联合模型, 将修改前后的答案同时纳入能力估计模型中估计被试的最终能力。van der Linden和Jeon (2012)使用该模型来检验纸笔测验中的异常修改行为, 结果显示通过模型残差的分析可以一定程度上诊断出异常修改行为。还有研究者从整合的视角, 将连续区块方法, 题目重排序方法与4PL模型相结合来减少允许题目检对估计精度的干扰(Yen, Ho, Liao,& Chen, 2012)。

1.4 问题提出

目前, 已经有一些方法可以实现允许题目检查的CAT。相比较而言, 连续区块方法有一定的实证研究基础, 结果也证实连续区块方法较为有效(Stocking, 1997; Vispoel et al., 1999, 2000, 2005)。此外, 基于连续区块方法的不足而提出的题目袋方法有其独特的优势, 也是一种有效的方法(Han,2013)。然而, 从前人的文献和研究结果中可以看出上述两种方法都存在一些不足。

连续区块方法存在以下不足: (1)被试无法跳过题目。这可能会使被试“卡”在某一题目上, 影响被试的整体发挥; (2)为了保证估计精度, 该方法需要设置较多的区块, 使得每个区块中题目数较少, 当限制被试只能在当前区块中进行修改时, 题目检查的自主性就会受到影响, 会造成被试额外的负荷,例如是否该进入下一个区块。

题目袋方法能够克服连续区块方法的不足, 但该方法依赖于设置合理的题目袋容量, 如果题目袋容量设置不合理会产生如下的问题：(1)如果容量太小, 难以提供充分的修改机会; (2)如果容量太大,由于题目袋中的题目不提供选题的信息, 因此较一般的CAT, 它选题的准确性和能力估计的精度都会受到影响; (3)Han (2013)发现, 当容量过大时, 低能力被试频繁地使用题目袋会影响 CAT对这部分被试的能力估计精度, 产生正向的估计偏差。

综上所述, 题目袋方法较连续区块方法能为被试提供更充分的修改自主性, 但它的有效性明显依赖于合理设置题目袋容量。如果有方法能够保证题目袋合理的设置, 就能改善和促进题目袋方法的应用。本研究认为通过结合连续区块方法和题目袋方法可以解决题目袋容量设置的问题, 弥补题目袋方法的局限, 并将这种新方法命名为区块题目袋方法(如图 1所示)。具体来说, 区块题目袋方法是将测验分成几个大区块, 为每个区块分配一个一定容量的题目袋。每个区块中的设置与题目袋方法一致。区块结束前, 被试需要作答完题目袋中的题目。进入下个区块后, 就不能再修改之前区块的项目。区块题目袋方法相对于连续区块方法, 它极大地减少了区块数量, 减少被试额外的心理负荷; 同时, 它能够改善题目袋方法对于题目袋的不合理设置, 因为区块的设置限制了被试只能使用当前区块下的题目袋, 并且只能在当前区块中进行修改。

本研究假设区块题目袋方法在允许 CAT题目检查的条件下, 比题目袋方法有更高的能力估计精度, 同时能够更好地应对作弊策略。

2 方法

2.1 研究设计

研究采用模拟研究的方式重复 25次, 每次通过模拟随机生成500个题目作为CAT的题库。假定题库由两参数逻辑斯蒂克模型(

Two-Parameter

Logistic Model

, 2PLM)校准, 题库中每个题目包含区分度

a

和难度

b

两个参数。

a

参数与

b

参数分别服从均匀分布

U

(0, 2)和

U

(‒3, 3)。从标准正态分布中随机抽取 5000名模拟被试的能力值, 每个模拟被试会在不同实验条件下作答一个 30题的定长CAT。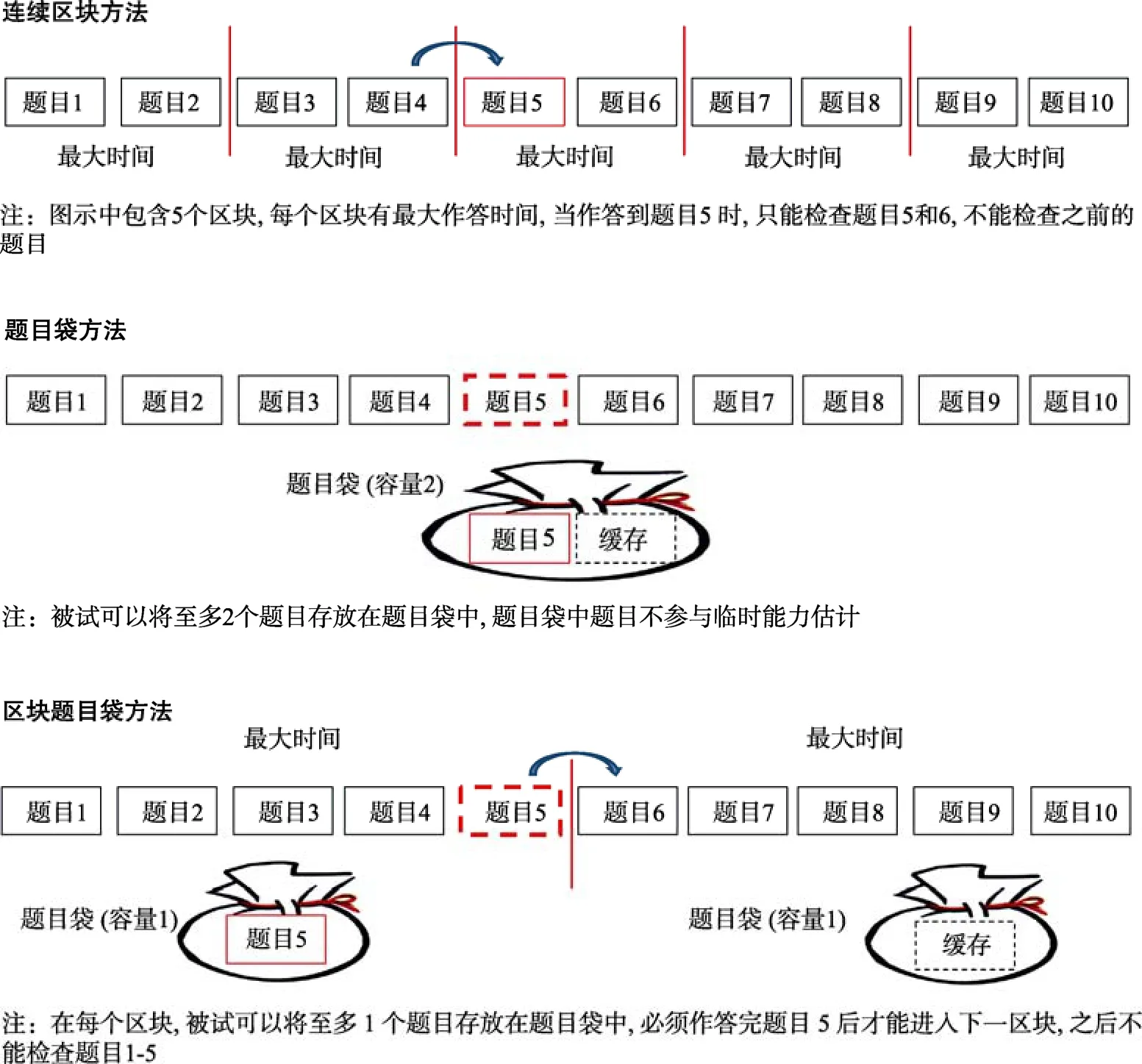

图1 连续区块方法, 题目袋方法, 区块题目袋方法示意图

在CAT的执行过程中, 初始题目从难度为‒0.5到0.5的题目中随机选择。随后采用极大费舍信息量选题策略从剩余题库中选择下一个题目。被试的能力估计采用期望后验估计(Expected A Posterior,EAP)和极大似然估计(

Maximum Likelihood Estimation

,MLE)相结合的方式。如果被试全部答对和答错或者作答少于5题时, 采用EAP方法估计被试的能力值; 否则采用MLE方法估计被试的能力值。

研究设置5种条件来检验区块题目袋的方法能否有效地实现CAT题目检查。5种条件包含了无修改条件和4种允许题目检查条件。无修改条件作为基线, 4种允许题目检查条件分别为1个区块×6容量题目袋、2个区块×3容量题目袋、3个区块×2容量题目袋以及6个区块×1容量题目袋。具体来说, 4种允许题目检查条件固定了题目袋总容量为 6, 使得总容量在4种条件间平衡。然后将6个容量题目袋平均分配到每个区块中。即4种条件下每个区块中包含一个6/n容量的题目袋(n = 1, 2, 3, 6)。需要注意的是, 1个区块×6容量题目袋的条件等同于题目袋方法, 后 3个为区块数不同的区块题目袋方法。研究设计之所以固定题目袋总量为 6, 一方面是出于模拟条件设置的考虑, 因为它能平均分配到不同的区块数中; 另一方面是因为6容量题目袋是Han (2013)研究中题目袋容量最大的条件, 希望通过设置比真实情境更极端的模拟情境, 来更有效地验证区块题目袋方法的可行性和优越性。6容量题目袋占了总题目数的20%, 已经远远超过了被试正常作答需要修改的量。

在无修改的基线条件下, 被试按照 CAT安排的固定顺序作答题目。但在4种允许检查的下, 被试可能会采用一种合理的作答策略(策略 1)和一种类似Wainer的作答策略(策略2)。前者是在区块题目袋方法下允许采用的作答策略, 后者是可能对测验公平性产生影响的一种作弊策略。因此, 研究分2部分进行, 策略 1模拟所有被试作答无修改条件和采用策略1作答4种允许题目检查条件; 策略2模拟所有被试作答无修改条件和采用策略2作答4种允许题目检查条件。通过比较各题目检查条件与无修改条件的平均偏差(BIAS)、差异均方根(

Root Mean Squared Error

, RMSE)、绝对误差均值(

mean absolute error

, MAE), 以及不同能力水平上的条件平均偏差(

Conditional BIAS

, CBIAS)、条件绝对差异均值(

Conditional mean absolute error

, CMAE)的大小来检验这两种策略下区块题目袋方法的估计精度。BIAS越接近与 0, 说明估计的偏差较小; MAE和RMSE越小且越接近基线水平, 说明CAT在该条件下对被试的能力估计精度较高。2种策略分别模拟25次。整个模拟过程通过 MATLAB R2013a软件(The Mathworks, Inc., 2013)编写程序实现。上述指标的计算公式如下：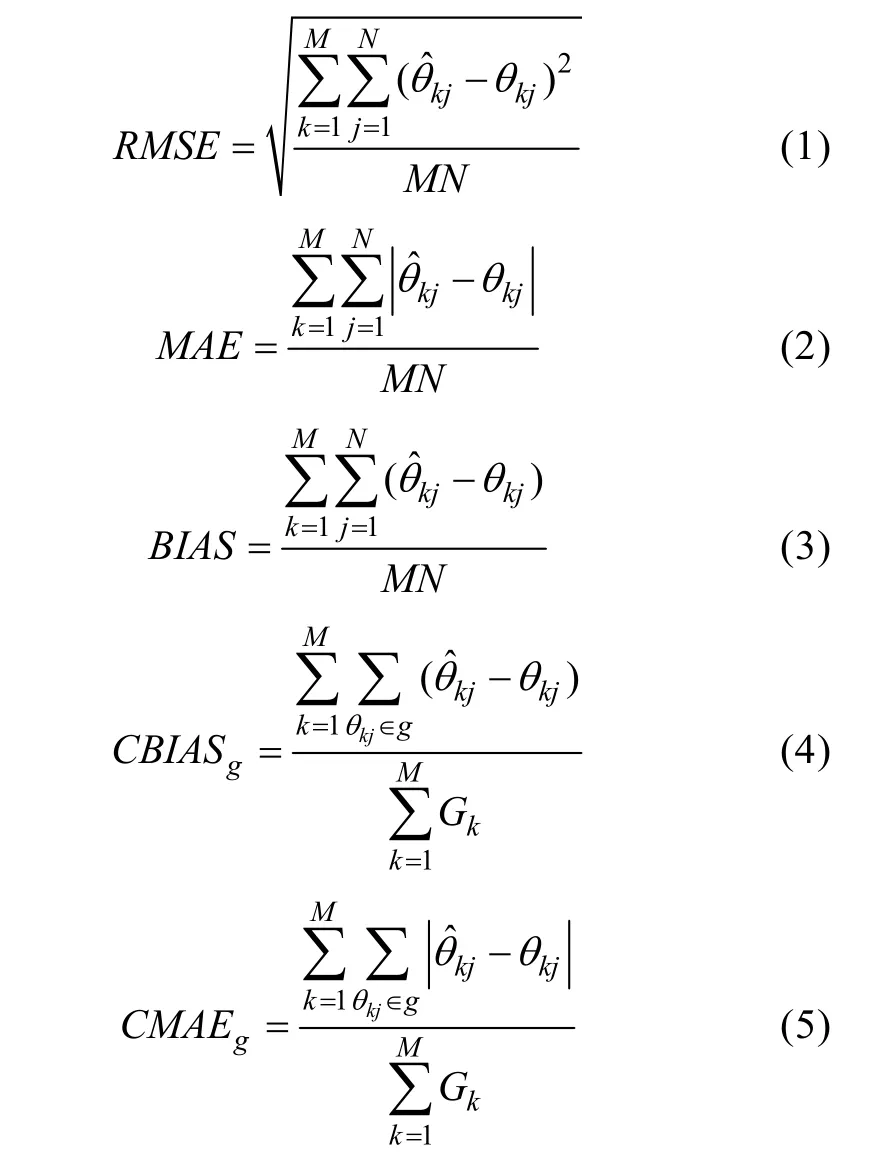

θ

: 第

k

次模拟中第j个被试的能力真值,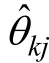

M

: 模拟总次数,

N

：每次模拟总人数,

G

: 第

k

次模拟中能力真值属于

g

组的被试人数

g

: 不同的能力水平组, 在

θ

量尺[‒3, 3]上每隔0.5个 logit单位获得, 12个组的取值分别为[‒3,‒2.5), [‒2.5, ‒2), …, [2.5, 3].

2.2 模拟策略1：合理作答策略

当允许被试检查题目时, 被试通常会标记出想要检查的题目以便之后修改。这种策略符合区块题目袋方法的运作机制, 被试可以利用题目袋存放想要检查的题目。一般来说, 被试会更倾向于标记较难的题目。模拟策略1就是基于这种合理作答策略(策略1)来检验不同条件下的能力估计精度。

研究1参照了Han (2013)对策略1的模拟过程。研究假定被试对越难的题目越倾向于放入题目袋稍后作答。在作答过程中, 被试通过判断题目的难易把更难的题目放入题目袋。当题目袋装满时, 被试会挑选题目袋中最简单的题目进行替换作答。对于题目难度判断的模拟, Han 基于 Vispoel等人(2005)研究结果的推论：当题目难度大于能力值0.5个单位时, 被试有 70%的概率判断为难; 当小于0.5个单位时, 被试只有 50%的概率辨别正确。本研究认为仅仅基于难度参数判断题目难易并不全面,题目的区分度参数同样会影响被试的作答正确率,从而影响被试对题目难度的感知。通过被试的正确作答概率来反映被试对题目难度的感知更符合逻辑。因此, 本研究基于“正确率越低越可能觉得题目难”这一逻辑来模拟被试对题目难易的判断, 即当被试的正确率为

P

时, 就有1‒

P

的概率判断为难题。

模拟策略1的CAT过程按如下步骤进行：(1)给被试选择作答题目; (2)被试判断题目的难易, 在模拟程序中通过产生一个0～1的随机数, 当1‒P大于这个随机数时, 即认为被试判断该题为难; (3)如果被试判断为难, 将题目放入题目袋中; (4)如果题目袋已满, 被试挑选最简单的题目进行替换作答, 在模拟程序中直接比较当前题目和题目袋中题目的正确率 P, 选择正确率最高的作答, 然后将剩余的题目继续存入题目袋; (5)直到区块结束, 被试需要给出题目袋中所有题目的最终答案; (6)进入下一区块, 重复上述步骤, 且不允许对先前区块中的题目进行检查和修改; (7)满足终止规则, 程序结束, 估计最终的能力估计值。模拟策略1假定所有被试均按这种策略作答。

模拟策略1之所以设计这种作答方式, 是为了反映一种十分极端的作答情境, 即被试充分利用题目袋, 始终坚持将难题放到之后作答的情境。如果在这样极端的情境下, 区块项目袋方法对能力估计有较好的精度, 那么在真实的CAT中表现会更好。

2.3 模拟策略2：类似Wainer作答策略

除了上述这种合理作答策略外, 在区块题目袋的方法中还可能存在类似 Wainer的作答策略。被试可以在题目袋容量范围内, 在测验开始时通过推迟作答把尽可能多的题目放入题目袋中, 之后再按正常方式作答(策略2)。在这个作答过程中, 被试存在故意“操纵”CAT选题的行为, 因此它同 Wainer策略一样是一种不合理的“作弊”策略, 但受限于题目袋容量, 被试只能操纵部分的题目, 而且模拟情境下低能力被试在合理作答策略下也会出现这种类似的Wainer的作答策略(例如当低能力被试认为初始几个题目都非常难)。因此, 为了避免误解, 我们称策略 2为类似 Wainer的作答策略。在策略 2情境下, 由于这些题目都是初始的中等难度题目,高能力被试就可以获得一部分与能力不符的简单题目。此外, 有研究表明CAT最初几个题目的作答正确与否对能力的估计有较大的影响(Chang &Ying, 2008), 如果题目袋容量充足, 被试可以自主挑选并答对最初的几个题目来“提高”自己的能力估计值。同时, 由于初始的题目提供信息极少, 这种策略会严重减少测验的信息量, 造成估计精度的降低。这些弊端随着题目袋容量的增大会变得愈加明显。因此, 检验不同条件在策略2下的估计精度显得尤为重要。

策略2的CAT模拟过程与策略1基本一致, 只是在策略1的基础上, 增加了Wainer策略的作答模拟, 即在每个区块开始时被试先将等量的题目放入题目袋中, 然后再按策略1的方式作答。策略2同样假定所有被试均按策略2的方式作答。

与所有模拟研究一样, 策略1和2均是基于概率模型进行模拟, 无法完全模拟真实测验中的所有作答行为, 考虑真实情境下心理因素的影响。因此在对结果的解释时应考虑到这个问题。

3 研究结果

模拟策略1的结果如表1所示。在题目袋、2区块、3区块、6区块及无修改5种条件下, MAE依次减小, 分别为0.1861、0.1845、0.1839、0.1827和 0.1817。4种允许检查的条件与无修改条件的MAE差值在0.0010～0.0044之间,考虑到4种允许修改条件下的MAE约为0.18, 低于0.005的较小增量完全可以接受。5种条件下的RMSE分别为0.2340、0.2321、0.2309、0.2298和 0.2284, 表明随着区块数的增加估计精度有略微提升, 区块题目袋方法要稍稍优于题目袋方法。5种条件下的BIAS分别为0.0009、0.0012、0.0017、0.0016和 0.0014, 所有允许检查条件下的 BIAS值都非常接近于 0, 而且与无修改基线差异不大, 总体上说明了区块题目袋方法可以实现题目检查而且不会导致能力估计的正向或负向偏差。总的来说, 在策略1的极端情境下,题目袋方法和区块题目袋方法不但提供了允许题目检查的功能, 而且没有过多地降低被试能力估计精度。区块题目袋方法较题目袋方法有更高的估计精度, 并且估计精度随着区块数量的增加而提高。

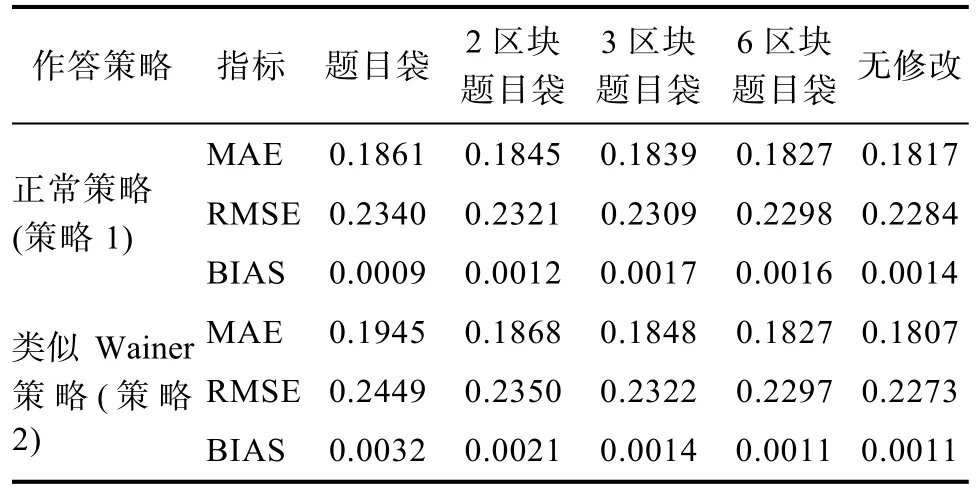
表1 策略1和策略2中5种条件下的各项指标值

虽然整体上题目袋方法和区块题目袋方法对能力估计精度的影响都在可接受的范围, 但仍然有必要考察不同能力水平上的CMAE和CBIAS来进一步比较两种方法在不同能力水平上的估计精度。结果如图2所示, 在12个区间为0.5个logit单位的等距能力组上, 4种允许题目检查条件下的CMAE基本上随着区块数的增长而降低, 最低的是无修改条件的CMAE。结果表明当被试都按策略1的作答方式作答时, 区块题目袋方法较题目袋方法在估计精度上有一定的提升。在中等和高能力水平上(

θ

> ‒1), 允许题目检查的4种条件估计精度相似,并没有出现明显的差异。但在低能力水平上[‒3, ‒1],4种条件的估计精度出现了较明显的差异, 题目袋方法的 CMAE要明显高于区块题目袋和无修改条件。尤其在[‒2.5, ‒3]的区间上, CMAE的差别最大,此时CMAE值分别为0.2268、0.2121、0.2085、0.2067和0.2002。题目袋方法的估计精度最差, 且与无修改条件相差 0.0266; 相反, 区块题目袋方法的估计精度只降低了0.0119、0.0073和0.0065。不难看出,区块的设置使区块题目袋方法能够更精确地估计低能力的被试。

对不同能力区间的CBIAS进行分析发现：5种条件下CBIAS的变化基本相似, 不存在明显差异。在低能力和高能力水平上分别出现约 0.01的负向偏差和正向偏差, 该偏差由 MLE估计方法本身的性质造成。在非极端的能力区间上, 偏差几乎都趋近于0, 并没有发现能力估计的系统性偏差。

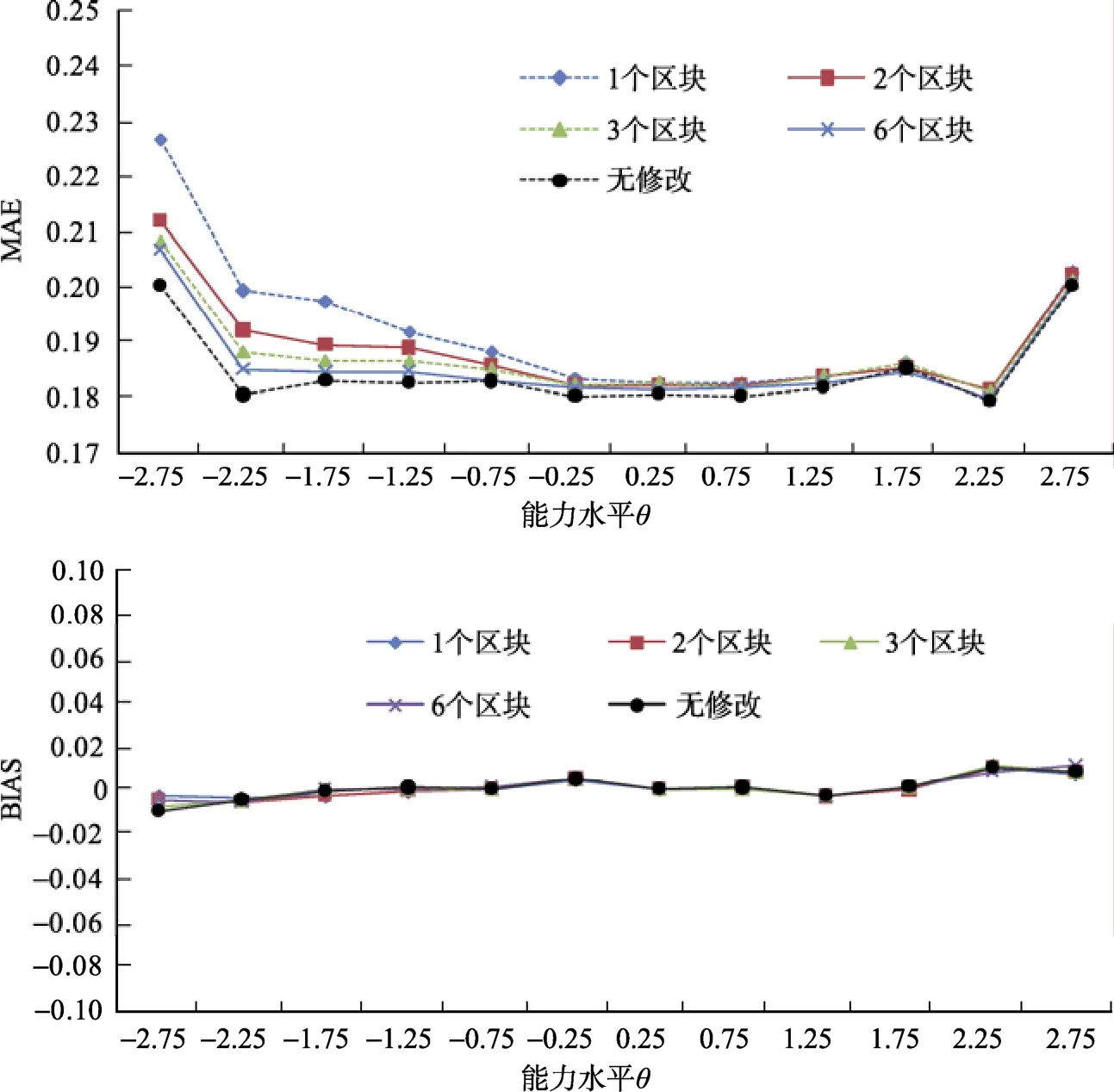
图2 合理作答策略下5种条件的CMAE和CBIAS

在策略1模拟研究的基础上, 模拟策略2进一步探究区块题目袋方法能否有效应对类似 Wainer作答策略, 即在所有被试采用类似 Wainer作答策略(策略2)的情境中, 4种允许题目检查的条件能否保持较好的能力估计精度, 同时有效防止被试利用策略2获得正向的能力偏差。策略2的模拟仍然把无修改条件作为基线与其他4种允许题目检查条件相比较。整体结果如表 1所示, 在题目袋方法、2区块、3区块、6区块及无修改5种条件下MAE依次减小, 分别为 0.1945、0.1868、0.1848、0.1827与0.1807, 允许题目检查条件与无修改基线条件差值分别为0.0138、0.0061、0.0041和0.0020。差异值较策略1的情境有所提高, 表明类似Wainer作答策略对被试能力估计的精度有更大的影响。在策略2中, 题目袋方法在估计精度上的劣势更为明显。与基线条件的MAE差异从策略1中的0.0044提高到了策略2中的0.0138, 明显超过区块题目袋方法的MAE差异增量, 说明策略 2对题目袋方法的能力估计精度影响更大。这也从侧面反映出区块题目袋方法的优越性。从另一指标RMSE来看, 同样得到了相类似的结果(见表1)。总的来说, 区块题目袋方法在估计精度上要优于题目袋方法。题目袋方法的问题可能在于当被试将在测验最初将过多的题目放入题目袋后, 这部分题目所能提供的信息量很少, 也不能为之后的选题提供充分的信息, 因此题目袋方法的估计精度出现了明显下降。这也是题目袋方法无法克服的问题。

虽然在策略2上题目袋方法的估计精度变得更差, 但所有允许题目检查条件均没有发现明显的系统性偏差。5种条件下的 BIAS分别为 0.0032、0.0021、0.0014、0.0011 以及 0.0011, 几乎接近于 0。虽然值很小, 但区块题目袋方法在控制偏差上确实要稍稍优于题目袋方法, 随着区块数的增加, 平均偏差也越接近无修改条件。因此, 总体上看4种允许题目检查条件不会产生较大的估计偏差, 被试无法通过类似Wainer作答策略获得额外的收益。

为了探究在策略2下4种允许题目检查条件在不同能力水平上的估计精度, 以及是否存在特定能力区间的被试能够利用策略2获得能力估计的正向偏差, 研究进一步考察不同能力水平的 CMAE和CBIAS, 结果如图 3所示, 在所有能力区间上,CMAE均随着区块数的增长而降低, 最高的是题目袋条件, 最低的是无修改条件。结果显示在策略 2的情境中, 区块题目袋方法较题目袋方法在各能力水平上的估计精度都有明显的提升。尤其在能力区间的两端, 区块题目袋方法有更好的估计精度, 随着区块数量增大, 估计精度就越接近基线条件。图中可以看到在极端能力水平上4种条件出现了较大的MAE差异。这种差异可能是由策略2的作答方式导致了题目袋方法无法通过初始的几个题目迅速定位被试的能力水平, 而且这些题目对极端能力的被试来说信息量不大, 导致对被试能力估计和随后的选题都不如无修改条件下那么精确, 而区块题目袋方法通过设置区块, 在作答最初几个题目时保证了更合理的题目袋, 并且在区块结束的时候及时地对能力估计进行校正, 使估计精度更加接近无修改条件。CBIAS的结果没有显著差异。能力两端出现了MLE估计方法导致的在极端能力上的微弱负偏和正偏, 其余能力水平上的bias都趋近于0。总的来说, 模拟研究的结果表明题目袋方法和区块题目袋方法都能有效地防止被试利用类似 Wainer作答策略获得正向的收益。 这是由于题目袋的限制,使被试无法持续操纵 CAT选择与其能力不符合的题目。然而, 题目袋方法无法应对策略2对其能力估计精度的影响。这是由于过大的题目袋在测验初始给了被试过大的自由, 导致了被试可以选择不答或选择作答最有把握的题目, 从而产生较大的能力估计误差。虽然总体上并没有系统性的偏差, 但很难保证个别被试不会获得较大的正向偏差。而区块题目袋方法能够更好地应对这种策略, 通过加入区块来减少当前被试可操纵的题目个数并对能力估计进行校正, 从而提高被试能力估计的精度。

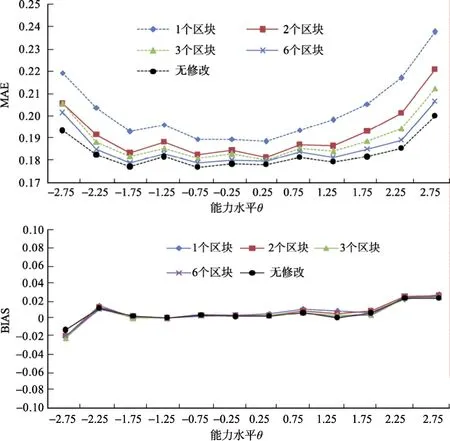
图3 类似Wainer作答策略下5种条件的CMAE和CBIAS

4 讨论

4.1 区块题目袋方法的优势

CAT在实际应用时, 被试无法检查并修改题目一直是一个没能妥善解决的问题(Wise, 1996;Vispoel, 1998; Papanastasiou & Reckase, 2007; Han,2013)。允许题目检查能够减少被试的焦虑等负面情绪, 让他们充分发挥自己的能力, 有利于准确估计被试的能力, 提高测验的效度(Olea et al., 2000;Stocking, 1997)。但是允许题目检查会降低CAT的估计精度, 而且当被试采用作弊策略作答时又会严重影响 CAT的精度与公平性(Wainer, 1993; Wise,1996)。

本研究提出的区块题目袋方法结合了连续区块(Stocking, 1997)和题目袋(Han, 2013)两种方法,弥补了题目袋方法的不足。区块题目袋方法不仅为被试提供自主修改题目的机会, 还能更有效地防止估计精度的降低, 应对相应的作弊策略。在区块题目袋方法中, 题目袋保证被试可以自主选择想要修改的题目, 区块的设置保证 CAT在执行过程中始终有一个合理的题目袋容量, 使得被试能力的估计更加精确。相比于连续区块方法, 区块项目袋方法只需要几个区块就能有效避免类似 Wainer作答策略对估计精度的影响, 被试不需要频繁地决策是否进入下一区块。 相比于题目袋方法, 研究结果显示在不同的作答情景中区块题目袋方法均要优于题目袋方法。在合理作答情境下, 随着区块数的增加,对低能力被试的估计精度越接近无修改的基线水平; 在类似Wainer作答策略情境下, 区块题目袋方法在所有能力水平上均优于题目袋方法, 在极高和极低的能力水平上尤为明显。

为了保证被试充分获得题目检查和 CAT的估计精度, 设置合理的题目袋容量是该方法适用的关键。Han (2013)的研究表明CAT的估计精度会随着题目袋容量的增加而降低。然而当测验有大量题目时, 题目袋的容量就不可避免地要增大, 这样上述的问题就会突显出来。在区块题目袋方法下, 这个问题得到了一定的改善。尽管题目袋的总容量相同,但区块题目袋方法在两种作答策略下均要优于题目袋方法。这是由于区块的设置, 使被试在作答过程中能使用的题目袋容量更为合理, 被试在获得检查机会的同时不会过度频繁地使用题目袋, 而且每个区块的结束都会校正能力估计值。尤其在策略2的情境中, 区块的设置使最初的题目袋容量更为合理, 避免被试在测验初始就将大量的题目放入到题目袋中, 防止了这种策略对 CAT执行过程和能力估计精度的影响。

在实际应用中, 被试对于题目的难度判断更为复杂, 会受到自身知识掌握情况, 练习情况等因素影响。当题目袋方法提供大容量的题目袋时, 被试可以利用它来挑选有把握的题目来保证完全作答对最初的几个题目, 由于 CAT中初始几个题的重要性要高于之后的题目(Chang & Ying, 2008), 这会严重影响被试的真实能力估计, 对测验公平性产生影响。而区块题目袋方法通过合理分配每个区块的题目袋, 能够有效地规避这一问题。

区块题目袋方法还可以根据测验开发者的不同需要, 自主地设置最优的区块数, 区块内题目数以及区块题目袋容量。为此, 测验开发者可以考虑采用一个综合性的指标来判断题目袋总容量和区块数设置是否合理。该指标称为相对题目袋容量比。表达式为Y=100P/TB, 其中T为题目数(常量),P为题目袋总容量, B为区块数。该指标含义是平均每个区块中题目袋容量与总题目数的比值。该指标是基于Han (2013)的研究以及本研究的结果推论所得, 即根据估计精度随着题目袋容量减少和区块数的增加而提高, 推断出相对题目袋容量比越小, 估计精度越好。一般来说题目袋的总容量约为题目总数的10%左右, 区块数5个左右为宜, 由此得出正常的相对题目袋容量比在2左右为宜。过小可能会使被试得不到充分的修改机会, 过大会导致估计精度的过度降低。当然, 上述结论仅仅是经验上的推论, 对于如何找到最优的相对题目比仍需要测验开发者在一定理论和实证研究基础上获得。这也是后续研究可以尝试的一个方向。

测验开发者也可以根据不同的测验目的有差别地分配题目袋容量到区块中, 例如觉得测验的初始题目至关重要, 那么可以在测验最初设置一个题目数和题目袋容量均较小的区块, 之后再设置更大的区块和题目袋容量。这样的设置只能在区块题目袋方法的框架下具有可行性。当然, 最优的配置仍然需要基于实证研究的结果得出。

4.2 允许题目检查的实践意义

除了关注区块题目袋方法的优势, 区块题目袋方法对实现 CAT题目检查所带来的益处也同样值得关注。区块题目袋方法为被试提供了一种类似纸笔测验的作答方式, 保证了被试对测验的控制感,减少他们的考试焦虑 (Olea et al., 2000; Vispoel et al., 2000)。被试能够按自己期望或习惯的方式作答题目, 犯更少的错误, 可以肯定的是允许题目检查能够减少测量误差 (Papanastasiou & Reckase, 2007)。此外, 在合理的区块和题目袋设置下, 被试可以更自主地分配作答的时间。被试在作答过程中发现某个题目太难无法作答, 可以选择放入题目袋中跳过进入下一个题目。被试在作答后面题目的同时, 随时调取题目袋中的题目进行检查, 这样被试无需为了做下一个题目而被迫对答案进行猜测, 也无需再花更多的时间在该题目上。这样能有效地提高时间的利用率, 也能减少测量误差。

模拟研究的结果发现无修改条件得到的结果始终优于允许题目检查的条件, 但这并不表明无修改的 CAT在实际应用中也是最好的。产生这种结果的原因是由于无修改条件模拟的是最理想的作答情境, 而允许题目检查条件模拟的是特定作答策略下的极端情境。然而无修改的 CAT在实际作答中会受到更多额外因素的干扰, 如考试焦虑。所以允许题目检查的 CAT可能在实际中会优于无修改的CAT。由于受到模拟研究的局限, 本研究无法进一步探究区块题目袋方法下的这些潜在优势。建议下一步研究可以采用实证的研究对区块题目袋方法进行深入探讨, 考察一些心理因素对它的影响。

4.3 研究不足

本研究模拟的是一个相对简单的情境：采用2PL模型、极大信息量方法的选题策略和测验长度为 30的定长终止规则, 因此对结果的概括和推广应当考虑这些限制。研究无法完全推论在不同的题库校准模型、选题策略、初始题目选择和能力估计方法下, 可以得到相同的结论, 研究者可以在不同的CAT条件下进一步探讨区块题目袋方法的有效性。

研究者还可以深入探讨在变长终止规则下区块题目袋方法的可行性。由于区块的存在, 该方法可以应用于变长的终止规则, 例如设定每5个题目作为一个区块, 并提供容量为 1的题目袋, 以此类推, 这样被试获得的修改机会基本上与他们的题量成正比, 只有在临近终止时可能出现微小的差异。当然, 在变长的终止规则下, 由于被试作答的题目总数不同, 相对题目袋容量比这一指标就无法适用,需要在变长规则下开发一个新的指标。

区块题目袋方法仍然有一定的局限, 比如它需要被试自主选择想要修改的题目, 因此被试无法改正作答过程中无意识犯的错误。虽然它仍然与纸笔测验的作答存在一些差异, 但它无疑更接近纸笔作答的方式, 较无修改的CAT有明显的进步, 具有重要的实践意义。

Benjamin, L. T., Cavell, T. A., & Shallenberger, W. R. (1987).Staying with initial answers on objective tests: Is it a myth?.In M. E. Ware & R. J. Millard (Eds.),

Handbook on student development: Advising, career development, and field placement

(pp. 45‒53). Hillsdale, NJ: Lawrence Erlbaum.Bowles, R., & Pommerich, M. (2001, April). An examination of item review on a CAT using the specific information item selection algorithm. In

The annual meeting of the National Council of Measurement in Education

. Seattle, WA.Chang, H. H., & Ying, Z. L. (2008). To weight or not to weight? Balancing influence of initial items in adaptive testing.

Psychometrika, 73

(3), 441–450.Chen, P., & Ding, S. L. (2008). Research on computerized adaptive testing that allows reviewing and changing answers.

Acta Psychologica Sinica, 40

(6), 737–747.[陈平, 丁树良. (2008). 允许检查并修改答案的计算机化自适应测验.

心理学报

,

40

(6), 737–747.]Chen, P., Zhang, J. H., & Xin, T. (2013). Application of online calibration technique in computerized adaptive testing.

Advances in Psychological Science, 21

(10), 1883–1892.[陈平, 张佳慧, 辛涛. (2013). 在线标定技术在计算机化自适应测验中的应用.

心理科学进展

,

21

(10), 1883–1892.]Han, K. T. (2013). Item pocket method to allow response review and change in computerized adaptive testing.

Applied Psychological Measurement, 37

(4), 259–275.Kingsbury, G. G. (1996). Item review and adaptive testing. In

Annual meeting of the National Council on Measurement in Education,

New York.Lord, F. M. (1983). Unbiased estimators of ability parameters,of their variance, and of their parallel-forms reliability.

Psychometrika, 48

(2), 233–245.Lunz, M. E., Bergstrom, B. A., & Wright, B. D. (1992). The effect of review on student ability and test efficiency for computerized adaptive tests.

Applied Psychological Measurement, 16

(1), 33–40.McMorris, R. F. (1991). Why do young students change answers on tests?.

ERIC Document Reproduction Service, ED 342803

.Olea, J., Revuelta, J., Ximénez, M. C., & Abad, F. J. (2000).Psychometric and psychological effects of review on computerized fixed and adaptive tests.

Psicológica,21

(1–2), 157–173.Papanastasiou, E. C., & Reckase, M. D. (2007). A “rearrangement procedure” for scoring adaptive tests with review options.

International Journal of Testing, 7

(4), 387–407.Stocking, M. L. (1997). Revising item responses in computerized adaptive tests: A comparison of three models.

Applied Psychological Measurement, 21

(2), 129–142.van der Linden, W. J., & Jeon, M. (2012). Modeling answer changes on test items.

Journal of Educational and Behavioral Statistics, 37

(1), 180–199.van der Linden, W. J., Jeon, M., & Ferrara, S. (2011). A paradox in the study of the benefits of test item review.

Journal of Educational Measurement, 48

(4), 380–398.Vispoel, W. P. (1998). Reviewing and changing answers on computer-adaptive and self-adaptive vocabulary tests.

Journal of Educational Measurement, 35

(4), 328–345.Vispoel, W. P., Clough, S. J., & Bleiler, T. (2005). A closer look at using judgments of item difficulty to change answers on computerized adaptive tests.

Journal of Educational Measurement, 42

(4), 331–350.Vispoel, W. P., Hendrickson, A. B., & Bleiler, T. (2000).Limiting answer review and change on computerized adaptive vocabulary tests: Psychometric and attitudinal results.

Journal of Educational Measurement, 37

(1), 21–38.Vispoel, W. P., Rocklin, T. R., Wang, T. Y, & Bleiler, T.(1999). Can examinees use a review option to obtain positively biased ability estimates on a computerized adaptive test?.

Journal of Educational Measurement, 36

, 141‒157.Waddell, D. L., & Blankenship, J. C. (1994). Answer changing:A meta-analysis of the prevalence and patterns.

The Journal of Continuing Education in Nursing, 25

(4), 155–158.Wainer, H. (1993). Some practical considerations when converting a linearly administered test to an adaptive format.

Educational Measurement: Issues and Practice, 12

, 15–20.Weiss, D. J. (1982). Improving measurement quality and efficiency with adaptive testing.

Applied Psychological Measurement, 6

(4), 473–492.Wise, S. L. (1996). A critical analysis of the arguments for and against item review in computerized adaptive testing. In

The annual meeting of the National Council on Measurement in Education

, New York, NY.Wise, S. L., Finney, S. J., Enders, C. K., Freeman, S. A., &Severance, D. D. (1999). Examinee judgments of changes in item difficulty: Implications for item review in computerized adaptive testing.

Applied Measurement in Education, 12

(2), 185–198.Yen, Y. C., Ho, R. G., Liao, W. W., & Chen, L. J. (2012).Reducing the impact of inappropriate items on reviewable computerized adaptive testing.

Journal of Educational Technology & Society, 15

(2), 231–243.