复杂约束条件下的再入轨迹迭代求解方法
2015-02-28张梦樱唐乾刚韩小军张青斌葛健全
张梦樱,唐乾刚,韩小军,张青斌,葛健全
(1. 国防科学技术大学 航天科学与工程学院,湖南 长沙410003;2. 第二炮兵装备部 高新技术办公室,北京100085)
0 引言
随着对高超声速滑翔飞行器研究的不断深入,满足禁飞区约束的滑翔轨迹优化问题逐渐成为了一个研究热点。满足飞行安全的同时,需兼顾复杂航路禁飞区约束,其轨迹优化问题将变得更为复杂。
在禁飞区建模方面,文献[1]建立了基于地理位置的威胁模型,将暴露危险作为优化目标设计最优轨迹。文献[2]考虑了威胁和目标可动,建立数学模型并采用遗传算法在线优化轨迹。文献[3]在平面地球假设下,建立无限长圆柱的禁飞区模型,设计了满足航路点和禁飞区约束的最优轨迹。文献[4]的禁飞区模型建立在球形地球表面,采用球面三角形原理建立无限长圆柱的空间禁飞区模型。文献[5]建立了半椭球的禁飞区模型,但未改变椭球赤道半长轴方向以适用更一般的情况。现有航路约束或禁飞区约束建模并不完全适用于实际情况,为使最优轨迹能够满足任务需求,有必要考虑更为复杂和真实的禁飞区模型。
复杂约束条件下的高超声速轨迹优化问题可归结为强非线性、多阶段、多约束的最优控制问题[6],对其求解十分困难。因具有收敛速度快和求解精度高的特点,伪谱法近年来发展迅速,成为求解复杂最优控制问题的常见工具。文献[5,7 -9]用Gauss 伪谱法求解包括端点、航路点和禁飞区约束的通用航空飞行器(CAV)轨迹优化问题。国内学者也研究了包括过载、动压、驻点热流等多约束轨迹优化问题[10-14]。在处理复杂路径约束问题时国内外研究者多采用分段优化的方法[5,8-9,11],有些会采用HP自适应伪谱方法求解[14-17]此类问题。然而当Gauss 节点较多时,处理复杂约束问题会存在设计变量数目庞大和约束众多,从而影响求解鲁棒性的问题[9,11]。同时,采用分段方法,也将增加设定设计变量初值的难度。
针对带有复杂禁飞区约束的高超声速滑翔飞行器轨迹优化问题直接采用伪谱法难以求解的问题,本文提出依序迭代求解策略。
1 数学模型
1.1 动力学模型
为简化计算,设地球为无旋圆球,在地心坐标系下建立飞行器的三自由度再入动力学模型[18]:
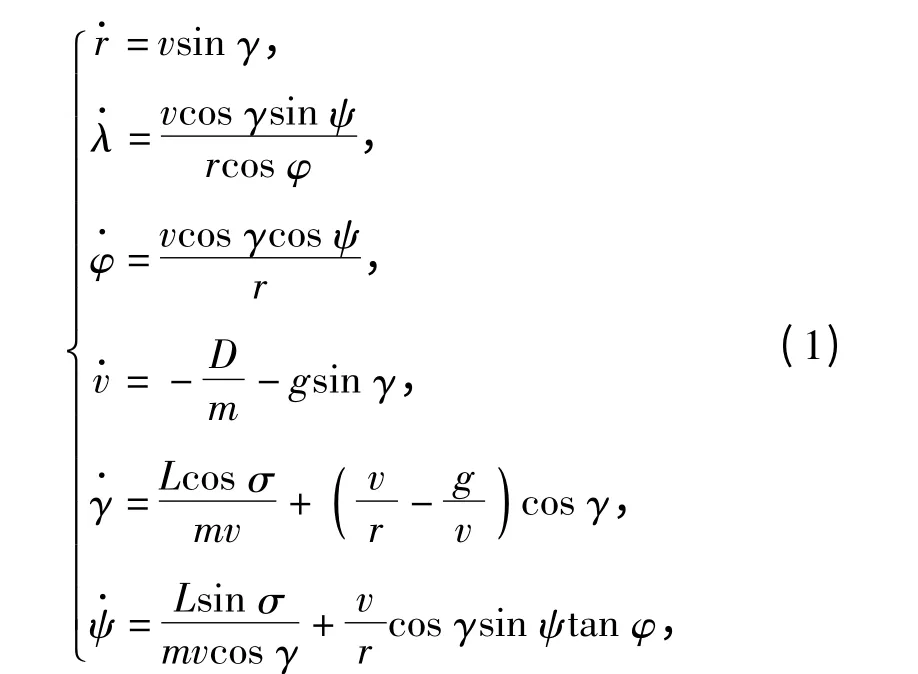
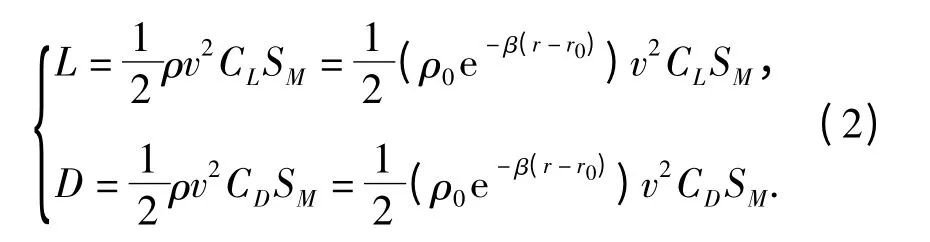
气动力系数通常是马赫数Ma 和攻角α 的函数,但因高超声速飞行器的气动遵循马赫数无关原则,可采用(3)式拟合,相应气动参数详见文献[15].
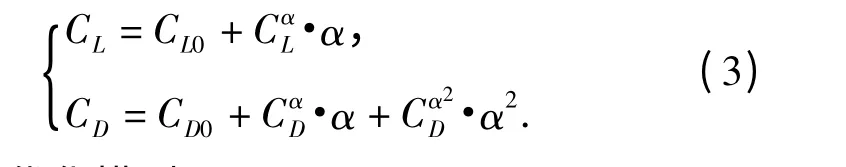
1.2 弹道优化模型
1.2.1 目标函数
对于指定目标点的再入轨迹优化问题,飞行时间是影响突防性能一个重要的优化目标。

式中:t0和tf分别为起始时间和终止时间。
飞行器在大气中的运动微分方程采用(1)式。
1.2.2 约束模型
考虑飞行器任务需求,需要考虑飞行器的指定端点约束,同时确保热防护安全、结构可靠性和姿态稳定性。
1)端点约束:
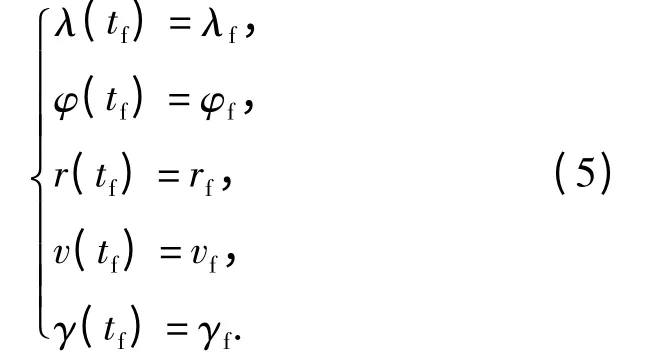
2)气动热约束[21]:
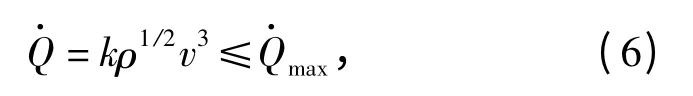
3)过载约束
再入段总过载通常较小,主要考虑法向过载ny的约束。
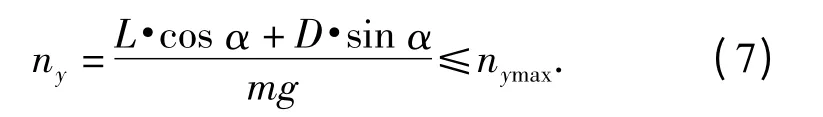
4)动压约束:

1.2.3 控制量选取
攻角α 和侧倾角σ 是影响飞行轨迹的重要变量,选取它们作为优化问题的控制变量,主要限制二者的取值范围,其表达式为
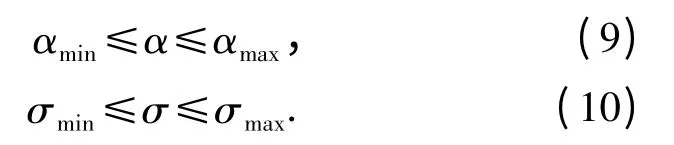
2 禁飞区参数化建模
禁飞区是指飞行过程中不允许经过的空域,如领空、防空识别区、雷达探测区和反导防御空域等。本文按边界地面投影类型分为规则和一般两类。规则禁飞区包括半球形、半椭球、椭圆柱和圆柱形,可建立参数化数学模型描述其覆盖范围。对一般禁飞区难于数学描述,可转化为若干规则型禁飞区的叠加组合。因此,典型规则形状禁飞区的数学建模是基础。
如图1所示,将地球球形表面某点(rnfz,λnfz,φnfz)作为禁飞区中心,以其为坐标原点建立禁飞区坐标系Ox1y1z1,其中Ox1轴指向禁飞区在过O 点切面上投影的短半轴方向,Oy1指向天,Oz1指向长半轴方向。αnfz为投影短半轴和正北方向的夹角,以顺时针方向为正。OeXeYeZe为地心直角坐标系,(r,λ,φ)为飞行器轨迹上某点坐标。
将以上定义的位置的球坐标转换到地心坐标系下:
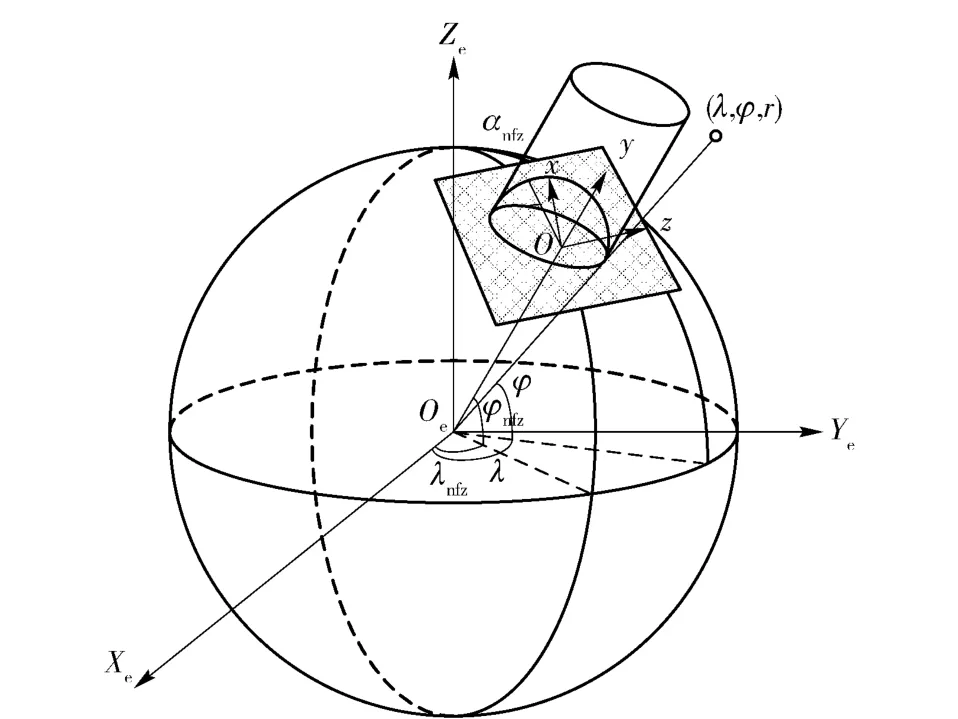
图1 禁飞区模型示意图Fig.1 Schematic diagram of no-fly zone model

式中:(x,y,z)和(xnfz,ynfz,znfz)分别为飞行器和禁飞区中心在地心坐标系下的坐标。
从地心系转化到禁飞区坐标系Ox1y1z1的转化矩阵为
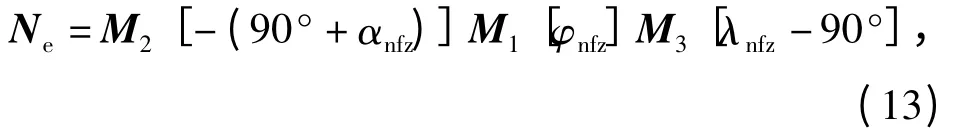
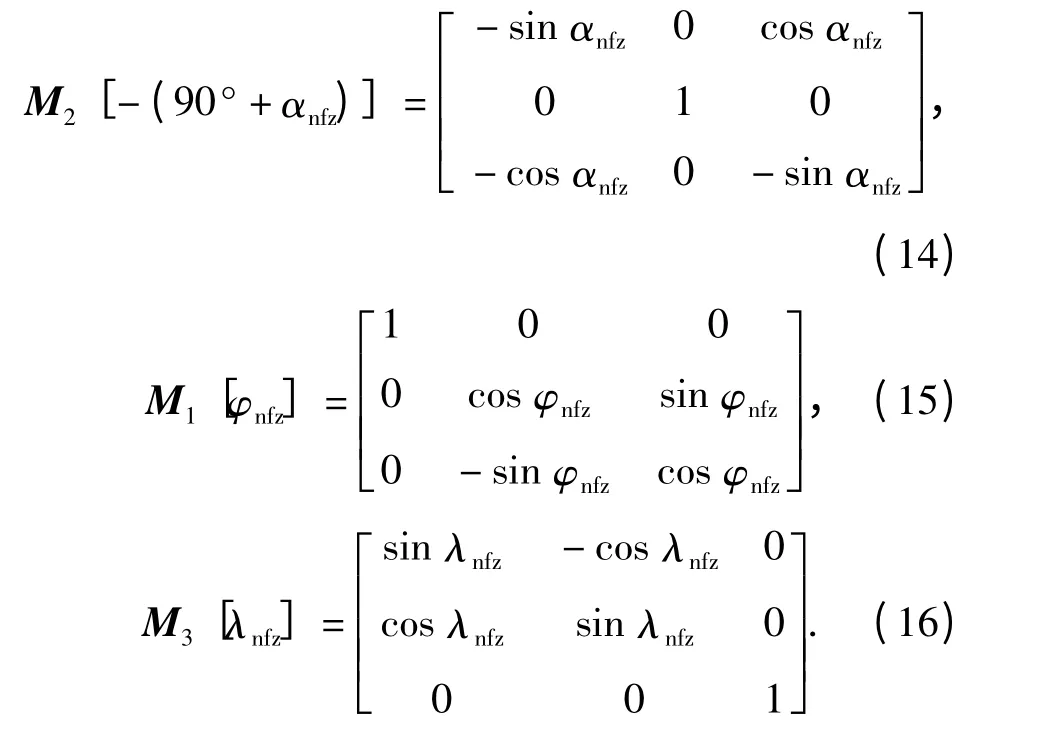
式中:M2、M1、M3表达式分别为
则飞行器在禁飞区坐标系下的位置坐标为
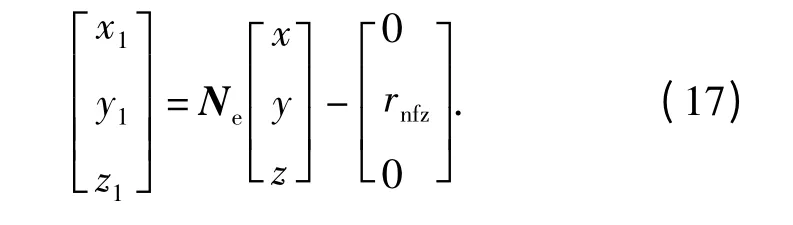
2.1 椭球禁飞区约束
椭球禁飞区约束可描述为
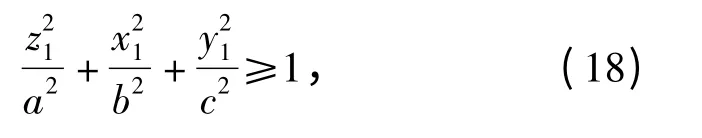
式中:a 为椭球赤道长半轴;b 为短半轴;c 为椭球的极半径。
特别地,当a=b=c 时,椭球禁飞区退化成圆球禁飞区。
2.2 无限高椭圆柱禁飞区约束
当c=inf 时,(18)式退化为
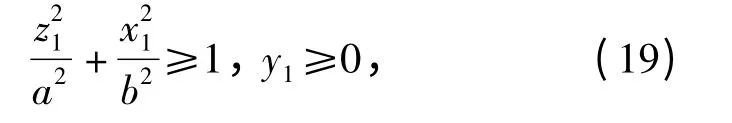
表示一个无限高椭圆柱禁飞区约束。
特别地,当{rnfz=re}∩{αnfz=0}∩{a =b}时,禁飞区退化成圆柱禁飞区,亦可用球面三角表示为
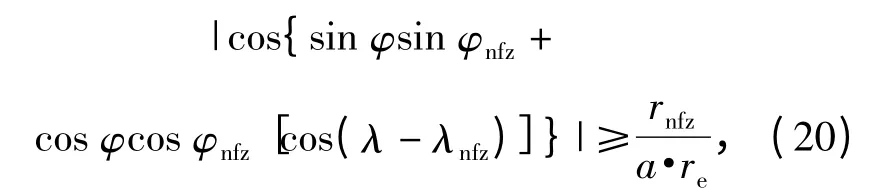
式中:rnfz为禁飞区在切平面上投影的半径,rnfz=a =b.
3 轨迹优化的迭代求解方法
3.1 伪谱法
近年来,伪谱法因具有收敛速度快和求解精度高的特点,成为求解复杂最优控制问题的常见工具[8]。影响伪谱法收敛速度和计算精度的主要因素有参数初值和离散节点的数量。由于伪谱法具有以较少的节点数获得较精确的解的优点,故参数初值成为主要因素[9]。伪谱法现广泛应用于轨迹优化问题中,但其算法性能仍受初值的影响[9]。
3.2 优化流程
考虑多约束的高超声速飞行器轨迹优化问题较为复杂,直接运用伪谱法求解将很难得到优化结果。同时,第2 节所建立的禁飞区模型的复杂程度也给直接优化增添难度。为解决上述问题,弥补算法对初值的敏感性并提高计算效率,考虑分段优化之外的方法,即采用如图2所示的基于Gauss 伪谱法的最优轨迹依序迭代串行求解流程。
依据各约束的复杂程度,逐步施加约束,并将优化成功得到的弹道作为下一步的初值弹道进行迭代。具体描述如下:
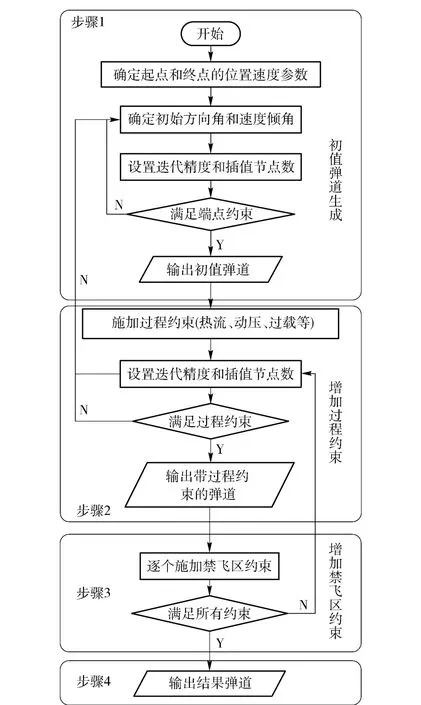
图2 优化流程Fig.2 Flow chart of optimization
步骤1 生成初值弹道。根据任务设定起点和终点的位置速度参数,拟定初始方向角和速度倾角,在GPOPS 软件中设定初值猜测范围、迭代精度和节点数,开始进行求解。若满足约束,则输出弹道。若不满足,则返回调整初值,直到得到优化结果。
步骤2 基于Gauss 伪谱法求满足端点约束和过程约束的最优解。优化模型中添加包括动压、驻点热流以及过载等过程约束,设置迭代精度和节点数,并将上一步所得优化结果作为下一步增加了约束的优化问题的初值弹道进行迭代求解。若结果满足约束,则输出弹道,若不满足,首先调整节点数,不能满足则返回上一步重新调整计算。
步骤3 求解满足端点约束、过程约束和禁飞区约束的最优弹道。如图3所示在优化模型中添加禁飞区约束。由2.3 节可得,所提出的禁飞区模型均可由椭球禁飞区模型退化变形得到,故首先添加半椭球禁飞区模型。为提高求解效率,加快收敛,考虑如下逐步扩大禁飞区大小的策略:
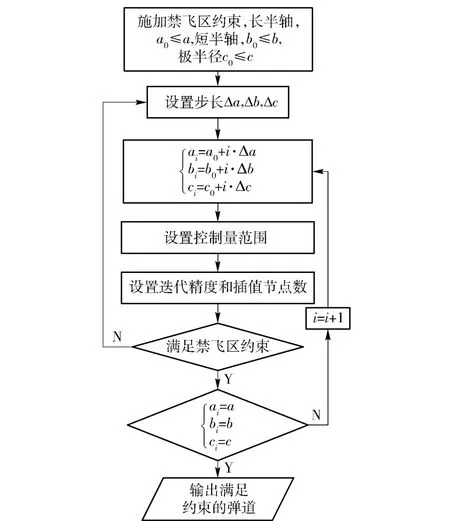
图3 禁飞区约束处理方法Fig.3 Process of dealing with no-fly zones constraint
设禁飞区加权的长半轴、短半轴及极半径分别为
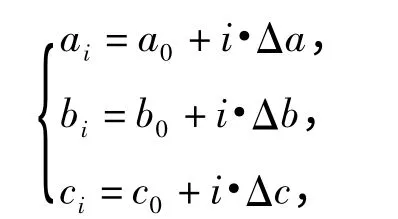
将每一步优化得到的可行解迭代到下一步,得到满足禁飞区约束的轨迹。如在这一步始终不能得到最优解,则返回步骤2 调整初值,重新优化弹道。
步骤4 检查结果是否满足所有约束,并判断收敛性,输出结果弹道。
4 仿真计算
4.1 仿真算例
根据前述的飞行器运动模型、优化模型和优化算法等,设计如下3 个算例:算例1 通过对经典算例的仿真计算验证了算法的正确性;算例2 对比不同禁飞区模型对优化结果的影响;算例3 对多组合禁飞区约束优化问题进行仿真,验证禁飞区模型的正确性和所提出计算方法的有效性。
4.1.1 算例1:算法验证
文献[19]所提出的最大横程算例,是典型最优控制问题的算例。设置初始参数如表1所示,采用所提出优化策略进行计算。

表1 仿真参数设置Tab.1 The values of simulation parameters
4.1.2 算例2:4 种禁飞区模型优化结构比较
在相同初始运动参数和端点约束条件下,以相同地理坐标为中心,规避某一特定区域,设置如下4 组禁飞区,以最小时间为优化目标,研究不同禁飞区模型对优化弹道结果的影响。为了严格比较4 种禁飞区模型优化结果,应用GPOPS 求解时,设置弹道分段数为10 段,数值计算精度为10-3,每段节点数最小为4,最大为8.
端点和禁飞区参数设置如表2、表3所示。
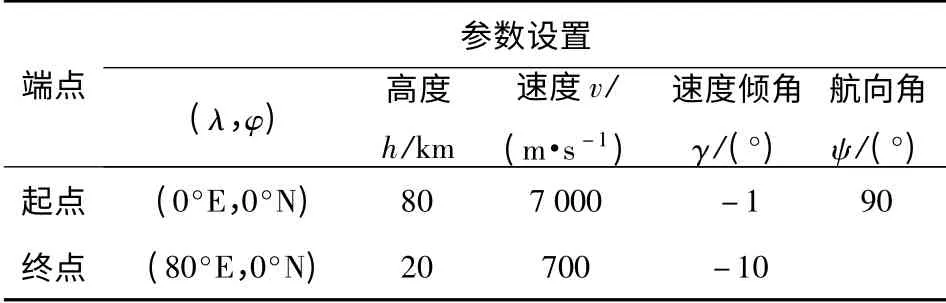
表2 端点参数设置Tab.2 The values of start point and end point
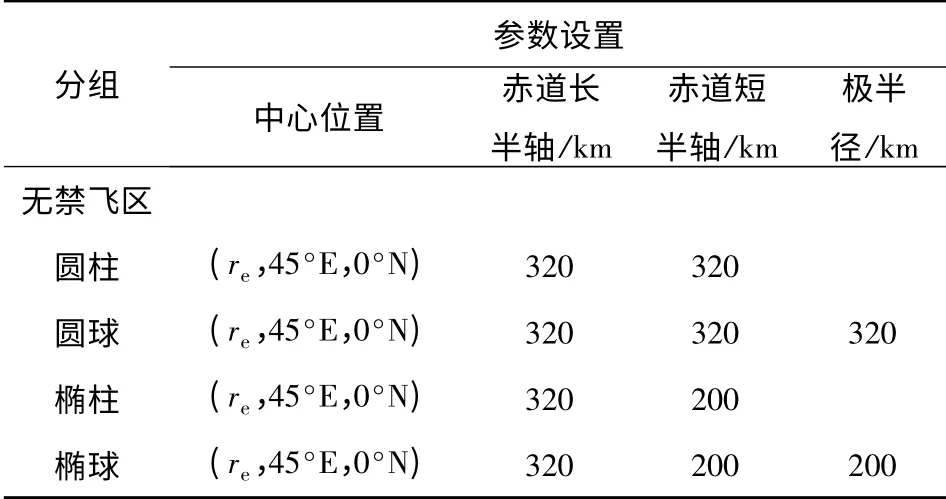
表3 不同禁飞区约束分组设置Tab.3 The values of different group of no-fly zone constraints
4.1.3 算例3:多组合禁飞区约束优化问题
考虑禁飞区约束的滑翔弹道优化问题,低速飞行器将其考虑成一个低空突防的航路规划问题[21]。文献[22]采用了遗传算法、航路极坐标编码方式、航迹适应度函数和遗传操作算子法进行仿真,却不适合高超声速条件下的轨迹优化问题。为满足禁飞区约束,采用Gauss 伪谱法进行弹道优化设计。
设计一条固定端点的时间最短飞行轨迹,在飞行过程中需绕过两个禁飞区。第1 个禁飞区模拟行政区域的领空,第2 个禁飞区模拟航母战斗群的防御半径。具体仿真数值设置如表4所示。

表4 多约束条件设置Tab.4 Multi-constraints
4.2 结果
4.2.1 算例1
本例仿真运算中,设置弹道分段数为10 段,精度为10-7,每段节点数最小为4,最大为8. 将所得=∞优化结果作为初值,迭代到添加热流密度约束的问题中,所得优化结果与文献[19]比较如表5所示。
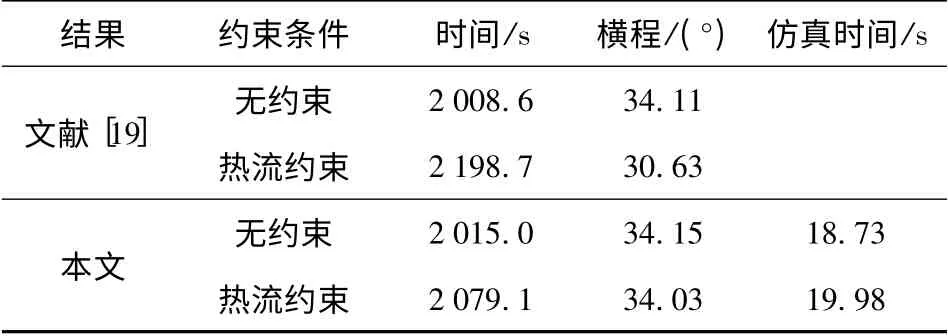
表5 优化结果比较Tab.5 Comparison of optimal results
本文优化所得结果中,无约束结果较好复现了文献[19]的结果。比较添加热流约束的结果,仿真得到全程驻点最大热流为795.14 kW/m2,考察热流极值约束满足情况,其误差为0.020 8%,满足精度要求。与文献[19]结果相比,在满足相同约束的情况下,优化目标最大横程更大,因而结果更优。同时,若采用直接添加约束进行优化,其仿真时间为38.70 s,相比迭代结果要慢。综上,可验证本文所提出方法的正确性。
4.2.2 算例2
在用伪谱法难以直接求解原问题的情况下,采用本文策略得到4 组优化时间分别为2 021.3 s、1 944.8 s、1 833.8 s 和1 828.5 s,对应图4第2 ~5 条轨迹结果。比较可得,球形禁飞区模型所得优化时间短于柱形禁飞区模型所得优化时间,且在4 种类型禁飞区均能满足规避如图阴影区域的情况下,椭球禁飞区对应时间最短,即结果最优。
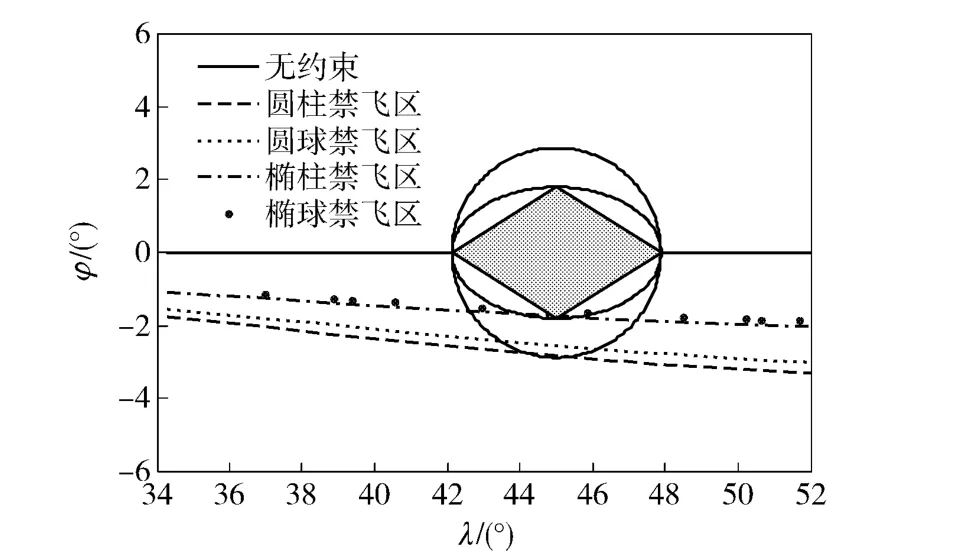
图4 优化轨迹局部投影Fig.4 Part ground projection view of optimal trajectories
4.2.3 算例3
类似地,由于本例约束复杂,伪谱法直接求解无法得到结果,采用3.2 节提出策略。运算中,设置弹道分段数为10 段,精度为10-3,每段节点数最小为4,最大为8. 取攻角α 和倾侧角σ 为优化变量,得到优化轨迹及其地面投影和结果如图5~图7所示。
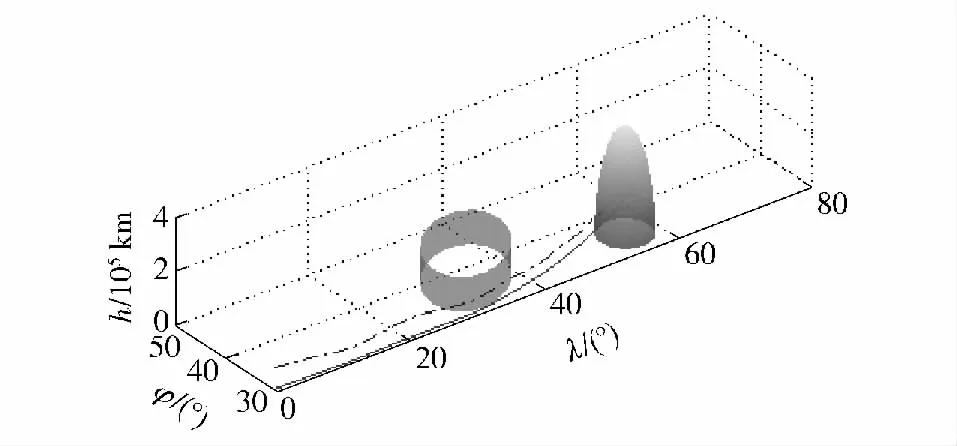
图5 三维优化轨迹Fig.5 3-D optimal trajectory
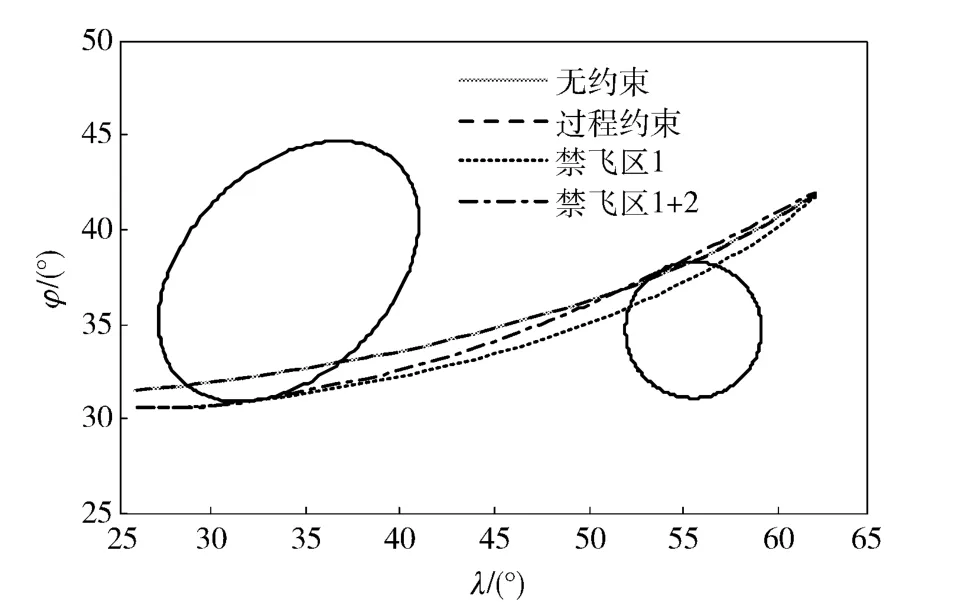
图6 优化轨迹地面投影Fig.6 Ground projection of optimal trajectories
图6为无约束和仅添加过程约束的两条轨迹穿过禁飞区,而添加禁飞区约束的优化结果满足所设置的路径约束,即从起点出发,先后绕过两个禁飞区的侧面实现规避。结果反映了4 条轨迹逐步逼近原问题最优解的过程。由图7(e)可见,控制量的变化满足了过程约束要求,且在滑翔段,攻角保持在17°附近,即对应最大升阻比攻角。由于所需规避区域距离较远,轨迹纬度变化平缓(见图7(c)),其地面投影呈不甚明显的“S”型,因而倾侧角在飞行过程中并未出现较大翻转,且对应规避动作时,角度变化率较为稳定,在工程上易于实现。由图7(h)~图7(j)可知,飞行器的驻点热流密度、法向过载及动压均满足了约束条件。同时,由图7可知飞行器终端参数λf=62.42°,φf=42.28°,hf=20 km,vf=712.62 m/s,γf= -10°,均满足设计要求。
在Windows XP 系统下,Matlab2009 计算平台下,采用第3 节描述的优化策略,从初值计算到优化结果的得到,仿真计算总耗时为4 036.1 s,约1 h,易于仿真实现。
5 结论
本文研究了复杂约束条件下的再入轨迹快速优化问题,从复杂约束的解构入手,建立了常用过程约束模型和更符合实际情况的典型禁飞区约束模型;针对采用Gauss 伪谱法所面临的初值敏感问题,提出依据复杂程度逐步添加约束的迭代求解策略;通过与文献[19]算例进行对比,验证了方法的正确性;分析了不同禁飞区模型适用的实际情况,并以仿真算例验证所建立模型的准确性;以时间最小为例设计了固定端点并考虑复杂约束条件下的最优轨迹。结果表明,依序逐步添加约束的迭代求解策略,不但能方便解决考虑多种禁飞区约束的问题,并且避免了Gauss 伪谱法在初值弹道生成上的难题,可作为分段求解轨迹优化问题方法的补充和参照。
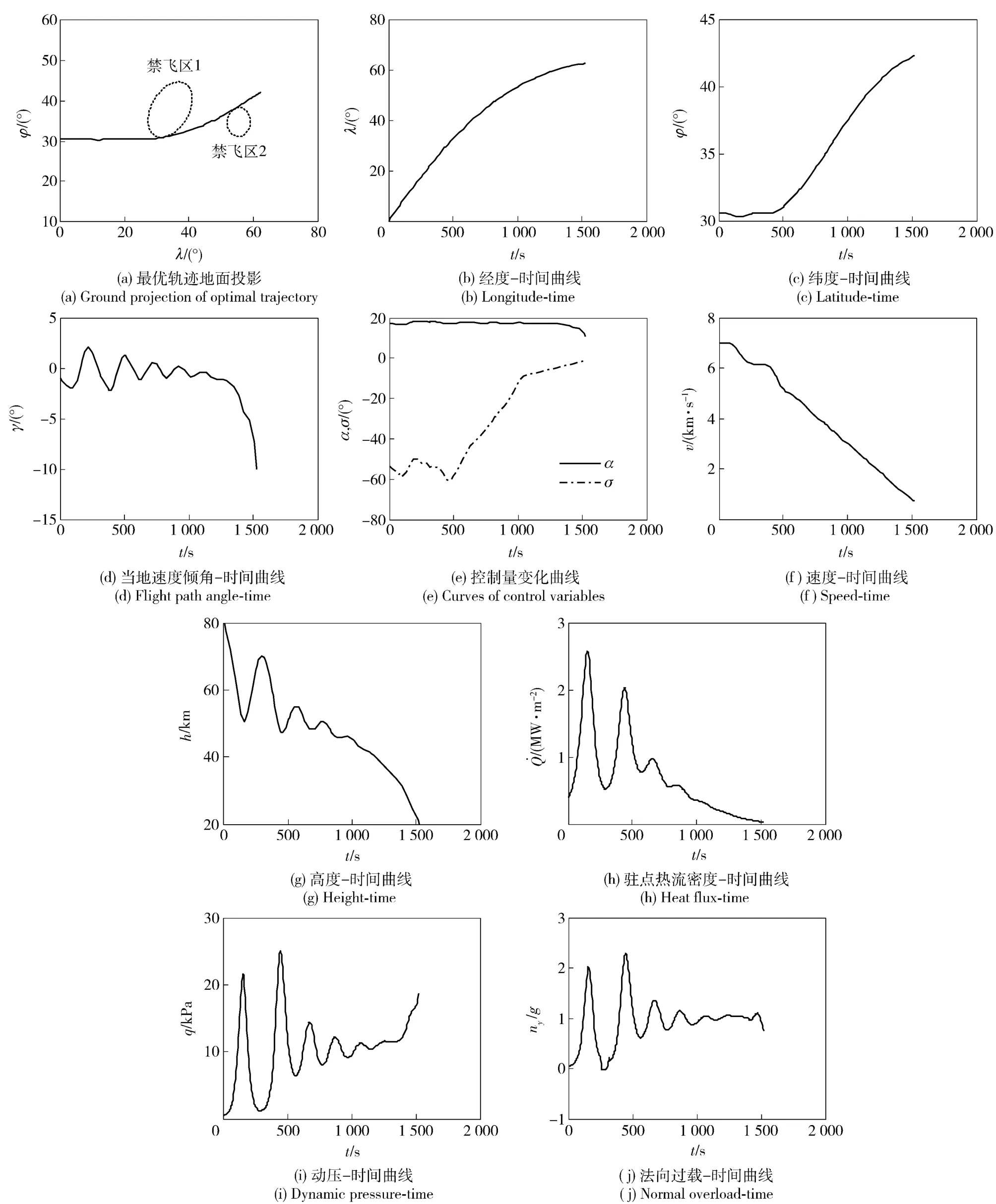
图7 优化结果Fig.7 Optimal results
References)
[1]Vian J L,Moore J R. Trajectory optimization with risk minimization for military aircraft[J]. Journal of Guidance,Control,and Dynamics,1989,12(3):311 -317.
[2]Twigg S,Calise A,Johnson E. On-line trajectory optimization including moving threats and targets[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit. Providence,Rhode Island:American Institute of Aeronautics and Astronautics,2004:2004 -5139.
[3]Jorris T R,Cobb R G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J]. Journal of Guidance,Control,and Dynamics,2009,32(2):551 -572.
[4]陈小庆,侯中喜,刘建霞. 高超声速滑翔式飞行器再入轨迹多目标多约束优化[J]. 国防科技大学学报,2009,31(6):77-83.CHEN Xiao-qing,HOU Zhong-xi,LIU Jian-xia. Multi-objective optimization of reentry trajectory for hypersonic glide vehicle with multi-constraints[J]. Journal of National University of Defense Technology,2009,31 (6):77 -83. (in Chinese)
[5]谢愈,刘鲁华,汤国建. 多约束条件下高超声速滑翔飞行器轨迹优化[J]. 宇航学报,2011,32 (12):2499 -2504.XIE Yu,LIU Lu-hua,TANG Guo-jian. Trajectory optimization for hypersonic glide vehicle with multi-constraints[J]. Journal of Astronautics,2011,32(12):2499 -2504. (in Chinese)
[6]李惠峰. 高超声速飞行器制导与控制技术[M]. 北京:中国宇航出版社,2012:242 -243.LI Hui-feng. Guidance and control technology of hypersonic vehicles[M]. Beijing:China Astronautic Publishing House,2012:242 -243.(in Chinese)
[7]Yaple D E. Simulation and application of GPOPS for a trajectory optimization and mission planning tool[D]. Ohio,US:Air Force Institute of Technology,2010.
[8]Jorris T. Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[D].Ohio,US:Graduate School of Engineering and Management,Air Force Institute of Technology,2007.
[9]雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙:国防科学技术大学,2008.YONG En-mi. Study on trajectory optimization and guidance approach for hypersonic glide-reentry vehicle[D]. Changsha:National University of Defense Technology,2008.(in Chinese)
[10]姚寅伟,李华滨. 基于Gauss 伪谱法的高超声速飞行器多约束三维再入轨迹优化[J].航天控制,2012,30(2):33 -45.YAO Yin-wei,LI Hua-bin. The generation of three-dimensional constrained entry trajectories for hypersonic vehicle based on the gauss pseudospectral method [J]. Aerospace Control,2012,30(2):33 -45.(in Chinese)
[11]Zhao J,Zhou R. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics,2013,26(6):1544 -1553.
[12]Sun Y,Zhang M. Optimal reentry range trajectory of hypersonic vehicle by Gauss pseudospectral method[C]∥International Conference on Intelligent Control and Information Processing. Harbin:IEEE,2011:545 -549.
[13]Liu P,Zhao J S,Gu L X. Rapid approach for three-dimensional trajectory optimization of hypersonic reentry vehicles[J]. Flight Dynamics,2012,30(3):263 -268.
[14]Darby C L,Hager W W,Rao A V. An HP-adaptive pseudospectral method for solving optimal control problems[J]. Optimal Control Applications and Methods,2011,32(4):476 -502.
[15]国海峰,黄长强,丁达理,等. 多约束条件下高超声速导弹再入轨迹优化[J].弹道学报,2013,25(1):10 -15.GUO Hai-feng,HUANG Chang-qiang,DING Da-li,et al. Reentry trajectory optimization for supersonic missile considering multiple constraints [J]. Journal of Ballistics,2013,25(1):10 -15.(in Chinese)
[16]王丽英,张友安,赵国荣. 改进的HP 自适应网格细化算法及应用[J].弹道学报,2013,25(1):16 -21.WANG Li-ying,ZHANG You-an,ZHAO Guo-rong. Improved HP-adaptive mesh refinement algorithm and its application[J].Journal of Ballistics,2013,25(1):16 -21.(in Chinese)
[17]洪蓓,辛万青. HP 自适应伪谱法在滑翔弹道快速优化中的应用[J].计算机测量与控制,2012,20(5):1283 -1286.HONG Bei,XIN Wan-qing. Application of HP-adaptive pseudospectral method in rapid gliding trajectory optimization[J]. Computer Measurement & Control,2012,20(5):1283 -1286.(in Chinese)
[18]赵汉元. 飞行器再入动力学和制导[M]. 长沙:国防科学技术大学出版社,1997:84 -85.ZHAO Han-yuan. Reentry dynamics and guidance of flight vehicle[M]. Changsha:National University of Defense Technology Press,1997:84 -85.(in Chinese)
[19]Betts J T. Practical methods for optimal control and estimation using nonlinear programming[M]. Philadelphia:Society for Industrial and Applied Mathematics,2009:247 -251.
[20]贾沛然,陈克俊,何力. 远程火箭弹道学[M]. 长沙:国防科学技术大学出版社,2009:155 -156.JIA Pei-ran,CHEN Ke-jun,HE Li. Long-distance missile ballistics[M]. Changsha:National University of Defense Technology Press,2009:155 -156.(in Chinese)
[21]文叶,姜文志,马登武. 飞机低空突防中的航路规划技术研究[J]. 飞行力学,2006,24 (2):22 -26.WEN Ye,JIANG Wen-zhi,MA Deng-wu. Study on the plane low-altitude penetration route planning technique[J]. Flight Dynamics,2006,24 (2):22 -26.(in Chinese)
[22]熊丹君,蔡满意,刘宇坤. 多约束条件下飞行器航路规划[J]. 弹箭与制导学报,2009,29 (2):289 -292.XIONG Dan-jun,CAI Man-yi,LIU Yu-kun. Air vehicle route planning for multi-constraints[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2009,29 (2):289-292.(in Chinese)
