天线罩寄生回路影响与自校正控制在线补偿

宗睿，林德福，范世鹏，2，兰玲

(1.北京理工大学 宇航学院，北京100081;2.北京航天自动控制研究所，北京100854;3.北京航天新风机械设备有限责任公司，北京100854)

0 引言

雷达导引头是雷达寻的导弹的核心部件，而天线罩作为雷达导引头的一种常用装置，起到保护天线、防止气流扰动及减小阻力的作用。天线罩的形状和材质会导致雷达波穿过天线罩时发生折射效应，造成瞄准误差角，进而生成寄生回路，对导弹制导系统的稳定性和制导性能造成严重影响［1-6］。

针对天线罩寄生回路带来的一系列不利影响，工程技术人员以解决工程实际问题为目的提出了一系列的补偿方法。内廓面修磨法［7］通过直接对天线罩内廓面某些位置进行修磨，以几何厚度的偏差来补偿天线罩材料介电常数的分散性，从而改善天线罩误差性能，但这种方法往往受限于制造工艺和加工水平。查表补偿法［8］是目前工程中常用的一种补偿方法，它首先对天线罩误差斜率进行地面标定，然后编制查表模块储存在弹载计算机中，在导弹飞行过程中通过实时查表插值对天线罩误差进行补偿。但是导弹飞行环境不同于地面，由于大气、温度等因素变化的影响，天线罩误差斜率会发生变化，同时地面标定往往需要耗费大量的时间，因此这种补偿方法的效果和效率都不甚理想。随着雷达寻的导弹对制导精度的要求越来越高，以上传统的补偿方法已经不能满足需求。近年来，在导弹飞行过程中对天线罩误差斜率进行实时估计并在线补偿的方法成为了研究的热点。Zarchan 等［9］提出采用抖动自适应的方法对天线罩误差斜率进行估计并补偿，但他只研究了常值天线罩误差斜率，并且这种加入抖动信号的方法对系统本身也有影响。Pini 等［10］设计了一个两步估计器来对天线罩误差斜率进行估计及补偿。Song 等［11］运用了多模型估计算法完成了天线罩误差斜率的估计和补偿。曹晓瑞等［12］将多模型估计算法和扩展卡尔曼滤波算法进行融合，实现了对变化的天线罩误差斜率的估计，并进行补偿。这些方法对系统模型及噪声水平的准确性要求很高，若与实际存在较大偏差则会严重影响估计和补偿效果。

针对上述问题，本文建立了天线罩寄生回路模型及其制导回路模型，研究了寄生回路对制导系统稳定性以及制导性能参数的影响，与此同时重点提出了一种基于极点配置自校正控制理论的天线罩寄生回路在线补偿方法。该方法在不需要了解具体系统模型参数以及估计天线罩误差斜率的情况下就可以有效地完成对寄生回路的补偿，从而降低天线罩寄生回路对制导系统的影响。

1 天线罩寄生回路建模

导弹在飞行过程中，目标发射或反射的电磁波经过天线罩时发生折射，导致雷达天线电轴发生偏移，此时导引头捕获的真实目标位置移到了视在目标位置，折射角Δq 为目标视线与视在视线的夹角，称为天线罩瞄准误差角。这个折射角通常较小，但它的变化速率会直接影响制导系统。电磁波入射角度不同会导致天线电轴偏移的角度不同，即导引头框架角φr不同，此时Δq 会随着框架角的变化而变化，记为

其曲线斜率称为天线罩误差斜率，定义为R，即

图1给出了天线罩误差影响下导弹与目标的相对几何关系。其中:qs为导引头指向角;qt为真实弹目视线角;q*为天线罩误差造成的虚假弹目视线角;ϑ 为弹体姿态角;ε 为导引头指向与真实弹目视线间的误差角;ε*为导引头指向与虚假弹目视线的夹角。

图1 天线罩影响下弹目几何关系Fig.1 Geometrical relation between missile and target under influence of radome

由图1可知，导引头测量到的实际视线角q*为

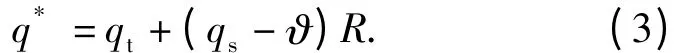
由(3)式可建立基于比例导引制导律的导弹典型制导动力学模型，如图2所示，其中:N 为导航比;vc为弹目相对速度;vm为导弹飞行速度;Tg为制导系统时间常数;Tα为攻角滞后时间常数;tgo为剩余飞行时间;n 为制导系统动力学阶数，在制导系统研究中一般取n≤5.

图2 天线罩误差影响的导弹制导动力学模型Fig.2 Missile guidance system model affected by radome error

由图2可知，由于天线罩误差斜率的影响，使得在制导回路内形成了2 条附加回路L1和L2. 其中回路L1的闭环传递函数为

由(4)式可知，天线罩误差斜率改变了导引头传递函数分母的常数项，但通常雷达导引头天线罩误差斜率R≪1，因此对导引头环节的稳定性和增益影响非常之小，在这里可将回路L1的影响忽略，保留回路L2，并将导引头、滤波器及驾驶仪环节合并，得到简化后的导弹制导动力学模型如图3所示。

图3 简化后导弹制导动力学模型Fig.3 Simplified missile guidance system model

由图3可知，在制导回路内，天线罩误差斜率的存在使得弹体姿态运动反馈至导引头，从而形成了一个包含导引头、制导滤波器及驾驶仪等高阶动力学的额外反馈回路，定义为天线罩寄生回路。在这里定义R ＞0 为天线罩寄生回路负反馈，R ＜0 为正反馈。由天线罩误差斜率的定义可知其符号具有不确定性，因此导弹在飞行过程中天线罩寄生回路正、负反馈均有可能存在。

2 天线罩寄生回路的影响

2.1 对制导系统稳定性的影响

图3所示的导弹制导系统闭环传递函数为

为了便于制导系统稳定性分析，对(5)式的闭环传递函数进行时间尺度无量纲化处理。令再令得到无量纲化后的闭环传递函数为

图4 天线罩寄生回路影响的制导系统稳定域Fig.4 Stable region of guidance system affected by radome parasitic loop

2.2 对制导系统性能参数的影响

由图3可知，当没有天线罩误差斜率影响时，导弹制导系统的制导时间常数近似为Tg，但是当天线罩误差斜率存在时，制导系统结构发生变化，天线罩寄生回路闭环无量纲传递函数为

其无量纲的有效制导时间常数可取(7)式分母中的一次项系数表示:

图5(a)给出了有效制导时间常数的变化情况。在寄生回路稳定的前提下，负反馈时随着K 值的增大而增大，且在同等K 值水平下，越大，越大。有效制导时间常数的增大会使制导系统变得“迟钝”，从而导致目标发生机动时产生较大的脱靶量。相反，正反馈时，随着K 值的增大而减小，且在同等K 值水平下，越大，越小。有效制导时间常数的减小虽然可以加快制导系统，但负天线罩误差斜率的存在会使得制导系统更易接近临界稳定状态，导致系统响应产生较大振荡，与此同时，干扰噪声更易进入系统并对其施加较大影响，因此同样会影响制导精度。

图5 天线罩寄生回路对制导系统性能参数的影响Fig.5 Guidance system parameters with radome parasitic loop

由(7)式可得比例导引的有效导航比为

图5(b)给出了有效导航比的变化情况，可知，负的天线罩误差斜率使得有效导航比增大，正的天线罩误差斜率使有效导航比减小。有效导航比过大会导致过载饱和，同时会放大噪声的影响。有效导航比过小则会导致导弹可用过载降低。这两种情况的出现都会影响最终的制导精度。

综上分析可以看出，天线罩寄生回路的存在使得制导系统稳定性、制导性能参数以及制导精度均受到了严重影响，因此，对天线罩寄生回路的补偿是非常必要的。

3 天线罩寄生回路在线补偿方法

3.1 极点配置自校正控制原理

自校正控制技术是一种将模型参数在线估计与控制器自动调整相结合的自适应技术［13］，它通过对模型参数的辨识，利用某种控制准则由控制器计算出相应控制量。当一些不确定因素引起模型参数变化时，系统能够实时辨识出变化的模型参数，并相应调整控制量，使得系统能够维持原有的良好控制性能，具有较强的鲁棒性。图6为自校正控制系统的典型结构框图。

图6 自校正控制系统结构框图Fig.6 Block diagram of self-tuning control system

极点配置自校正控制策略就是把极点配置设计方法作为控制准则引入到自校正控制系统的控制器参数设计中，从而使得实际的系统闭环极点始终收敛于设定的期望极点，保证系统良好的稳定性和动静态性能。

设原有被控对象采用如下离散数学模型［14］:

式中:d 为系统延时;A(z-1)=1 + a1z-1+ … + anaz-na;B(z-1)= b0+ b1z-1+ … + bnaz-na;A(z-1)与B(z-1)互质。

设自校正系统的参考输入为yr(k)，要求设计控制器，使得系统输出y(k)与参考输入yr(k)之间的传递函数为

式中:Gm(z-1)为期望传递函数;Am(z-1)的极点为期望极点。控制量u(k)可以用参考输入yr(k)和系统输出y(k)的线性函数来表示，如图7所示。

图7 极点配置自校正控制框图Fig.7 Block diagram of pole placement self-tuning control

由图7所示可得控制量为

式中:H(z-1)、F(z-1)、G(z-1)为待定多项式。yr(k)和y(k)之间的传递函数为

极点配置自校正的任务就是通过模型参数辨识在线实时得到被控对象模型A(z-1)和B(z-1)，从而寻求多项式H(z-1)、F(z-1)和G(z-1)，使得闭环系统的传递函数Gp(z-1)始终等于期望的传递函数Gm(z-1)，即

3.2 递推阻尼最小二乘算法

在整个极点配置自校正控制过程中，对被控对象的模型参数辨识是最为关键的一步，如果模型参数辨识与真实模型参数存在较大偏差，则会直接影响控制器参数的求解，从而大大降低极点配置自校正的控制效果。递推阻尼最小二乘法(RDLS)［15］是递推最小二乘的改进算法，它通过引入遗忘因子和阻尼系数来加强算法的适应性和稳定性。

设被辨识模型的差分方程为

将上式写成向量的形式:

式中:h(k)=［-y(k-1)，-y(k -2)，…，-y(k -n)，u(k -1)，u(k -2)，…，u(k -m)］，为系数矩阵;θ=［a1，a2，…，an，b1，b2，…，bm］T，为待估的模型参数;υ(k)是均值为0 的随机噪声。递推阻尼最小二乘的递推公式为

3.3 在线补偿方案设计

为了贴合实际情况且研究方便起见，将图3中的制导控制动力学阶数取n =4，且拆分为导引头，滤波器以及自动驾驶仪环节，分别表示为s/(Tss+1)，1/(Tfs+1)，1/(T2ms2+2μmTms +1). 天线罩误差斜率的存在导致寄生回路的生成，改变了原有制导系统的结构，因此可以得到天线罩寄生回路的闭环传递函数为

由(16)式可知，天线罩误差斜率改变了特征方程原有的一次项和常数项系数，导致系统极点位置发生改变，从而影响整个制导系统性能。在这里将整个天线罩寄生回路作为被控对象，并将原有的不受天线罩误差影响的制导系统动力学Nvcs/［(Tss +1)(Tfs +1)(T2ms2+2μmTms +1)］作为期望传递函数，采用极点配置自校正控制，使得寄生回路传递函数实时收敛于期望传递函数，从而在不需要辨识出天线罩误差斜率的情况下，完成对寄生回路的实时在线补偿。

由于需要利用递推阻尼最小二乘辨识对被控对象进行模型参数辨识，因此要建立天线罩寄生回路离散传递函数。表1给出了一组典型雷达制导导弹制导系统参数。

取天线罩误差斜率R=0，采样时间T =0.01 s，将表1中的参数代入(16)式中并采用0 阶保持器进行离散化，得到不受天线罩误差影响的离散系统为

表1 典型制导系统参数Tab.1 Typical parameters of guidance and control system

由(17)式可知，系统时延d =1，分母和分子的阶数分别为4 阶和3 阶，因此可设被控对象为

被控对象中各系数［a1，…，a4，b0，…，b3］为未知数。与此同时，设期望特征方程为Am(z-1)=1 -3.683z-1+ 5.090z-2 -3.128z-3 +0.721z-4.

由(14)式可知，采用极点配置自校正后闭环系统的传递函数分子和分母的阶次都高于期望传递函数分子分母的阶数。因此要使闭环传递函数的阶次与期望传递函数的阶次相同，闭环系统传递函数的分子分母必须进行零极点相消，但零极点相消只能消掉稳定因子，不能消掉不稳定因子。为了防止被控对象零点出现不稳定因子，在这里将B(z-1)作为一个整体不进行零极点相消。此时，可令Bm(z-1)=B(z-1). 由于必须保证AF+z-1BG 与HB 之间有公因子，因此公因子只能是H. 在这里设公因子为H=A0(z-1)，由于A0为被零极点相消的公因子，因此不能为不稳定因子或是阻尼特性差的因子，最好保证A0的根在阻尼特性较好的区域为宜。

将(11)式分子和分母都乘A0，可得

式中:F(z-1)= f0+ f1z-1+ … + fnfz-nf;G(z-1)=g0+ g1z-1+…+gngz-ng;A、B 均可通过RDLS 获得，且阶数已知。当Am与A0确定以后，若可求出多项式F(z-1)和G(z-1)，则证明(19)式有解，表明系统特征方程可以收敛至期望特征方程Am，即极点可以配置到指定位置。

当A、B 互质时，满足(19)式的解有无穷组。为使问题有确定的、唯一的并且是最简单的解，在这里设定(19)式中AF(z-1)与z-1BG(z-1)的阶次相同，同时等式右边的阶次小于等于左边的阶次，因此可得多项式的阶次需满足以下要求:

由(20)式可得:deg G=3，deg F=3，deg A0≤3.为使(19)式左右两边阶数相等，取deg A0=3，并设A0(z-1)=(1 -0.6z-1)3. 因此，根据(19)式可得如下Diophantine 方程:

图8 天线罩寄生回路在线补偿流程框图Fig.8 Block diagram of radome parasitic loop compensation

使用极点配置自校正补偿方法的好处在于不需要知道具体的导弹弹体参数和系统模型参数，也不必辨识出天线罩误差斜率，只需要确定制导系统的动力学阶数就可以对被控对象和期望传递函数进行设定，从而完成极点配置自校正控制过程，避免了使用卡尔曼滤波等估计算法时，由系统模型准确度带来的估计精度问题。

4 仿真及结果分析

为了验证控制算法的有效性，对图8所示的极点配置自校正寄生回路补偿算法进行仿真。仿真过程中，制导系统参数取表1中所示参数，初始被控对象离散模型为(17)式所示。系统输入设为正弦函数q(t)=0.01 +0.005sin (πt)，在参数辨识中，加入均值为0、方差为1.5 的随机白噪声，同时取方差矩阵初始值为P0=108I，遗忘因子λ =0.85，阻尼系数μ=0.6. 采样时间取T =0.01s，仿真时间为tf=20 s.

4.1 仅天线罩误差斜率变化影响

在被控对象中引入随时间变化的天线罩误差斜率R，为了考察R 在不同类型的变化条件下极点配置自校正控制的补偿效果，在这里引入两组R 的取值，分别为方波变化形式和正弦变化形式:

需要指出的是，当R = -0.1 时，寄生回路刚好处于临界稳定状态，因此当-0.1 ＜R ＜-0.05 时，寄生回路稳定，当-0.15 ＜R ＜-0.1 时，寄生回路不稳定。

由以上初始条件开始仿真，图9和图10 所示为不同R 影响的情况下极点配置自校正补偿效果。

图9 R=R1(t)时自校正补偿效果图Fig.9 Self-tuning compensation for R=R1(t)

从图9和图10 所示的仿真结果可以看出，在未做任何补偿措施的情况下，制导系统的输出在天线罩寄生回路的影响下产生剧烈振荡并趋向于发散。这表明整个系统的稳定性能十分恶劣。采用极点配置自校正的补偿算法之后，无论天线罩误差斜率R发生突变或者保持平稳变化、当前天线罩寄生回路处于稳定或者不稳定状态，自校正系统的输出总是能较好地跟踪期望输出，避免了系统输出发散趋势的出现。这表明天线罩寄生回路带来的影响基本消除，自校正后的制导系统稳定性得到了良好的改善，对于外部环境的改变同样具有良好的自适应性，在噪声影响下，自校正系统依然保证了较好的跟踪性能，因此也体现出了较强的鲁棒性。

图10 R=R2(t)时自校正补偿效果图Fig.10 Self-tuning compensation for R=R2(t)

4.2 天线罩误差斜率与模型参数共同变化影响

导弹自动驾驶仪是针对导弹飞行过程中某一个特征点而设计的，而当导弹处于不同的飞行高度或者飞行马赫数时，弹体参数会发生变化，从而导致驾驶仪性能发生改变。

导弹飞行高度不同会导致攻角滞后时间常数Tα发生变化，这里假定Tα按照如下规律实时变化:

假定导弹速度vm按照如下规律实时变化:

导弹飞行高度与速度的变化同样导致驾驶仪性能发生改变，假定驾驶仪时间常数与阻尼系数按照如下规律实时变化:

对于天线罩误差斜率的变化，取

由(23)式～(26)式所示条件开始仿真，图11给出了RDLS 的模型参数在线辨识情况。

图11 RDLS 模型参数在线辨识Fig.11 On-line identification of model parameters of RDLS

由图11 所示仿真结果可以看出，由于Tα、vm、Tm、μm以及R 为时变参数，因此对象模型参数也相应随时间发生了不同程度的变化，对于这种参数时变的情况，采用RDLS 依然能够有效地进行参数实时在线辨识，被辨识参数能够较好地收敛至真实值，没有出现发散的情况，体现了该算法较好的收敛性、适应性与稳定性。

利用模型在线辨识参数可实时进行期望极点配置。图12 给出了天线罩误差斜率与模型参数共同变化时极点配置自校正补偿效果图。

图12 R 与模型参数共同变化时自校正补偿效果图Fig.12 Self-tuning compensation in the change of R and model parameters

图12 所示仿真结果表明，即使天线罩误差斜率与模型参数共同发生变化，自校正系统的输出仍然可以较好地跟踪期望输出，消除了天线罩寄生回路以及模型参数变化对系统带来的影响。

4.3 对脱靶量的影响

为了验证自校正补偿算法对导弹制导精度的改善情况，在这里将图8所示的天线罩寄生回路自校正系统代入到图3所示导弹制导回路模型当中，考察导弹在目标常值机动和速度指向误差分别影响下天线罩寄生回路自校正前后的脱靶量情况，如图13所示。

在仿真过程中，取各参数随时间变化如下:

图13 引入自校正补偿的制导回路模型Fig.13 Model of guidance loop with self-tuning compensation

由此可得在不同的末导时间tf下，目标常值机动和速度指向误差分别影响的导弹脱靶量如图14所示。

图14 自校正补偿后的脱靶量水平Fig.14 Miss distance after self-tuning compensation

由图14 的仿真结果可以看出:在未做补偿的情况下，导弹脱靶量在天线罩寄生回路及模型参数时变的共同影响下无法收敛，已经趋于发散;采用自校正补偿之后，导弹脱靶量水平与无参数变化影响的脱靶量水平基本一致，且当末导时间tf＞5 s 时逐渐收敛到0. 这表明自校正补偿算法基本消除了模型参数变化以及天线罩寄生回路对于导弹脱靶量的影响，制导精度得到了很大程度的提升。

综上所述，极点配置自校正补偿算法可实时在线辨识出系统模型参数，并实现了对天线罩误差斜率的补偿，大幅度减小了寄生回路对制导系统稳定性、制导性能参数以及制导精度带来的不利影响，从而证明该补偿算法是行之有效的。

5 结论

对于雷达寻的导弹来说，天线罩误差带来的寄生回路问题将对导弹的制导系统带来非常严重的影响。经研究表明:天线罩寄生回路严重削弱制导系统稳定性。负反馈时，制导系统稳定性对天线罩误差斜率敏感度较低，但受动力学阶数影响较大。正反馈时制导系统更易失稳，但对动力学阶数并不敏感。随着tgo的减小，制导系统的稳定域有减小的趋势，所能容忍的最大天线罩误差斜率下降，特别在寄生回路正反馈时表现得更为显著。寄生回路负反馈会增大有效制导时间常数及减小有效导航比，而正反馈则会减小有效制导时间常数和增大有效导航比，这两种情况都会对制导精度产生不利影响。所提出的极点配置自校正在线补偿方法不需要知道具体的系统模型参数，也不必辨识天线罩误差斜率，只需要知道系统动力学阶数并设定相应的期望传递函数就可以在线完成对寄生回路的补偿，并且具有良好的适应性和鲁棒性，起到了增强制导系统稳定性，提升制导性能的作用。

References)

［1］Garnell P. Guidance weapon control systems［M］. Shrivenham，Oxfordshire:Royal Military College of Science，2003:288 -293.

［2］Nesline F W，Zarchan P. Radome induced miss distance in aerodynamically controlled homing missiles［C］∥AIAA Guidance ＆Control Conference.Seattle，US:AIAA，1984:99 -115.

［3］Lin J M，Lin C H. Intelligent fuzzy terminal guidance law for high altitude air defense by taking tuning rate and radome error slope into consideration［C］∥Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications. Beijing:IEEE，2011:723 -727.

［4］Susumu Miwa. Radome effect on the miss distance of a radar homing missile［J］. Electronics and Communications in Japan，1998，83(7):14 -22.

［5］Mihaita A，Gheorghe G. The influence of radome on radar antennas system［C］∥Proceedings of 9th International Conference on Communications International Conference on Communications. Bucharest，Romania:IEEE，2012:151 -154.

［6］Palumbo N F，Blauwkamp R A，Lioyd J M. Basic principles of homing guidance［J］. Johns Hopkins APL Technical Digest，2010，29(1):25 -41.

［7］戎华，曲晓飞，杨美建，等. 关于减小天线罩瞄准误差的补偿方法的研究［J］. 系统工程与电子技术，2005，26(7):1135 -1141.RONG Hua，QU Xiao-fei，YANG Mei-jian，et al. Research on the compensation method of decreasing a radome＇s boresight error［J］.Systems Engineering and Electronics，2005，26(7):1135 -1141.(in Chinese)

［8］管俊琦，曹旭东，冯振明. 天线罩瞄准误差的建模和补偿方法［J］. 电光与控制，2011，18(1):66 -68.GUAN Jun-qi，CAO Xu-dong，FENG Zhen-ming. Modeling and compensation method of missile radome error［J］. Electronics Optics ＆ Control，2011，18(1):66 -68.(in Chinese)

［9］Zarchan P，Gratt H. Adaptive radome compensation using dither［J］.Journal of Guidance，Control，and Dynamics，1999，22(1):51 -57.

［10］Pini G，Jeremy K. Improving missile guidance performance by in-flight two step nonlinear estimation of radome aberration［J］.IEEE Transactions on Control System Technology，2004，12(4):532 -541.

［11］Song T L，Shin S J. Active homing performance enhancement with multiple model radome slope estimation［C］∥AIAA Guidance，Navigation，and Control Conference. Rhode Island，US:AIAA，2004:931 -940.

［12］曹晓瑞，董朝阳，王青，等. 基于EKF 的天线罩误差斜率多模型估计方法［J］. 航空学报，2010，31(8):1608 -1613.CAO Xiao-rui，DONG Chao-yang，WANG Qing，et al. Radome slope estimation using multiple model based on EKF［J］. Acta Aeronautica et Astronautica Sinica，2010，31(8):1608 -1613.(in Chinese)

［13］徐湘元. 自适应控制理论与应用［M］. 北京:电子工业出版社，2007.XU Xiang-yuan. Adaptive control theory and applications［M］.Beijing:Publishing House of Electronics Industry，2007. (in Chinese)

［14］李言俊，张科. 自适应控制理论及应用［M］. 西安:西北工业大学出版社，2005.LI Yan-jun，ZHANG Ke. Adaptive control theory and applications［M］. Xi＇an:Northwestern Polytechnical University Press，2005.(in Chinese)

［15］刘金琨，沈晓蓉，赵龙. 系统辨识理论及MATLAB 仿真［M］.北京:电子工业出版社，2013.LIU Jin-kun，SHEN Xiao-rong，ZHAO Long. System identification theory and MATLAB simulation［M］. Beijing:Publishing House of Electronics Industry，2013. (in Chinese)