计算热力学及其在材料科学中的应用

Bo Sundman，Matthias Stratmann，张利军，杜勇

(1.原子能委员会萨克雷研究中心 国立核科技学院，法国)(2.鲁尔-波鸿大学，先进材料多学科中心，德国 波鸿 D-44780)(3.中南大学 粉末冶金国家重点实验室，湖南 长沙 410083)

计算热力学及其在材料科学中的应用

Bo Sundman1，Matthias Stratmann2，张利军3，杜勇3

(1.原子能委员会萨克雷研究中心 国立核科技学院，法国)(2.鲁尔-波鸿大学，先进材料多学科中心，德国 波鸿 D-44780)(3.中南大学 粉末冶金国家重点实验室，湖南 长沙 410083)

摘要：简要综述了材料科学领域中计算热力学与动力学的模型、数据库、软件及应用。介绍了当前最常用的软件。详细解释了用于描述不同相热力学性质的重要模型，以及获取热力学数据库中模型参数的优化过程。此外，还阐述了平衡计算中最常用的一种算法。最后本文给出了一些使用软件和数据库计算相平衡和相图，以及结合动力学数据用于相变及其过程模拟的示例。

关键词：计算热力学；动力学模拟；相变；软件；数据库

1Background

The thermodynamic laws have been known for more than 100 years, slightly longer than the theory of quantum mechanics. But the rapid development of computer hardware and software during the last 30 years have transformed these sciences from something all knew about but rarely bothered about to useful tools applicable to multicomponent materials and other systems.

Most of the software used in materials science for multicomponent thermodynamic calculations are proprietary and software is not open and the published algorithms are not very clear. This is the case for FactSage[1], Pandat[2], MTDATA[3], Thermo-Calc[4]to mention only those that have developed extensive databases for alloys and related materials.

There are many other speciallized software, for example in geology with very high pressures, for polymers or restricted to a few components. But in this review we will only deal with software, databases and applications oriented towards multicomponent alloy systems.

Quantitative description of microstructure evolution during material processes is the key to novel material design. As the highly development of computational thermodynamics and computational kinetics, the computer aided design of materials now can simulate and predict the microstructure evolution during materials processes to a quantitative degree. For instance, DICTRA (DIffusion-Controlled TRAnsformations) simulation package[5], with the full integration of multicomponent thermodynamics and kinetics, is capable of simulating diffusion controlled phase transformations in multicomponent alloy systems. Moreover, phase-field simulations including effects of interfacial energy, stress, strain and convective transport in liquid, represent a new class of simulation tools in materials science[6-8]. The link to the reliable thermodynamic and kinetic databases is of invaluable benefit for quantitative phase-field simulations.

2Thermodynamic models and databases

A detailed review of thermodynamic modelling and the assessment technique can be found in the book by Lukas et al[9], here only a bref summary is given. The thermodynamic databases contain model parameters assessed from experimental and theoretical data.

2.1Modelling the integral Gibbs energy of each phase

In Computational Thermodynamics (CT) the integral Gibbs energy for each phase in a system is modelled separately as they can be very different, such as gas, liquid, and intermetallics etc. The total Gibbs energy for a system is expressed as:

(1)

At constant T,P and overall composition, the Gibbs energy will be at a minimum at equilibrium. For other conditions the equation can be modified using Lagrangian multipliers as will be explained in the next section 3.

2.1.1The pure elements and the lattice stability concept

The pure elements must have the same reference state in all phases and this is called the Stable Reference State (SER) and is the stable state for the element at 298.15 K and 1 bar. To describe the Gibbs energy for the element A at any other T or P there are an expression:

(2)

The current thermodynamic databases do not describe any properties below T=298.15 K but at a recent workshop discussions were made how to model an extention down to 0 K[10]. This will require that models for the heat capacity at low temperature are implemented.

Some elements heve a ferromagnic transition and this is modelled separately using a phenomenological equation proposed by Inden[11], which is added to eq. 2.

magnG = RTf(τ)ln(β + 1)

(3)

(4)

where R is the gas constant, TCis the Curie temperature andβis the Bohr magneton number. The funtion f(τ) is different above and below TCand describes the contribution due to the magnetic ordering. See the book by Lukas et al[9]for details.

The lattice stability concept introduced by Kaufman in his book[12]is an essential part of the modelling of solution phases. This concept means that the elements must have well-defined Gibbs energy values also for phases for which they are not stable as pure elements. The reason for this is that the Gibbs energy surface for a multicomponent solution phase must have an endpoint for each pure element also if the element is not stable for this phase. In order to combine assessments of several binary and ternary systems such endpoints, called endmembers of the solution phase, must be the same in all assessments. In 1991 the SGTE group[13]proposed an extended pure element database including also heat capacity data and this is kept updated on their website[14]. The Gibbs energy for a pure element in any phase is thus be expressed as a function of T and P, irrespectivly if the phase is stable or not for this element.

In the original Calphad technique no heat capacites were used for the lattice stabilities, all phases were assumed to have the same heat capacities. However, this created problems in particular for the elements with a magnetic transition like pure iron. One could say that the introduction of different heat capacities for the phases was the start of CT. Note that the SGTE pure element database normally adopts the same heat capacity expression, except for any magnetic contribution, for the metastable phases of an element as for its stable phase.

2.1.2Compounds with fixed composition

For a phase, α, with fixed composition of the elements A and B we can use a generallisation of eq. 2 to describe its Gibbs energy at any T and P:

(5)

2.1.3Solution phases and the compound energy formalism

For solution phases with a crystal lattice a very general formalism called the compound energy formalism (CEF)[15, 9]is used. As constituents any species can be used and thus CEF includes models for gases, regular solutions, interstitial solutions, intermetallics and long range ordering as special cases.

For any model the molar Gibbs energy for any phase can be explained in terms of the general expression

(6)

For a phase with several sublattices the concept of endmembers, denoted I has been introduced to specify a compound with one specific constituent in each sublattice, i.e. a compound. The Gibbs energy of an endmember is written as °GIα. Compare with eq. 15 below for the partial Gibbs energy of an endmember.

The surface of reference is given by:

(7)

∏YI=yi,1yi,2...yi,s

(8)

where yi,sare the constituent fractions of the constituents i specified by the endmember I in the sublattice s. Wherever obvious the phase superscript is omitted.

In CEF the configurational entropy assumes random mixing on each sublattice

(9)

where asis the site ratio of sublattice s. The excess Gibbs energy describes interactions between constituents on the same sublattice, with consideration of the constituents on the other as explained in Lukas [9].

The magnetic contribution has already been described but the important feature for a solution phase is that the temperature for magnetic ordering, TCand the Bohr magneton number, β are modelled as composition dependent properties and the magnetic contribution will thus vary with these.

2.1.4The reciprocal sublattice model

The simplest system where the sublattice model has some unique features in the so called reciprocal system with two sublattices and two constituents in each:

(i,j)a(k,l)b

where i and j are constituents on the first sublattice with a sites and k and l are constituents on the second sublattice with b sites. There are many examples of phases with such a model for example an interstitial solution of C in the austenite in the Fe-Ti system:

(Fe,Ti)1(C,Va)1

or the Laves-C14 phase in the Fe-Ti system modelled with anti-site defects:

(Fe,Ti)2(Ti,Fe)1

where the C14 is the Structurbericht designation.

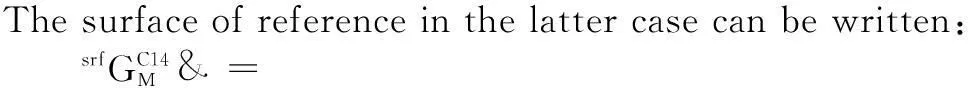
(10)

(11)

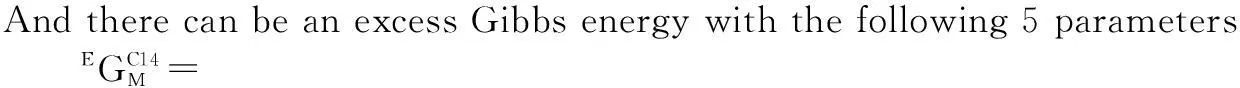
(12)

where the first 4 are normal regular solution parameters giving the interaction energies between two constituents on the same sublattice with a single constituents on the other. These can also be composition dependent, see Lukas et al.[9]. The last parameter is called a reciprocal interaction parameter with simultaneous interaction in two sublattices. This has been shown to be useful to model short range ordering in solids[17].

2.1.5 The chemical potential and the partial Gibbs energy for endmembers

With several components we have an amount, NAand also a chemical potential, μAfor each component A. The definition of the chemical potential for component is:

(13)

The values of T,P and the amount of all other components, B, are fixed when calculating the chemical potential for A.

As there are frequent mistakes calculating the chemical potential for models of the Gibbs energy we give first the expression for the partial Gibbs energy for a phase modelled with a single set of sites, where the constituent fractions are the same as the mole fractions,

(14)

(15)

For a phase with sublattices it may not be possible to calculate the partial Gibbs energy with respect to the components but one can always calculate the partial Gibbs energy with respect to the endmembers. This expression is

(16)

where the subscript is represent the constituent i in sublattice s as specified by the endmember I. The summation over j is for all constituents. For a derivation of this see[18-19].

2.1.6Models for defects, chemical potentials and dilute solutions

The models currently used in CT have been developed gradually over many years and may look unnecessary complex for many simple cases. But we must be careful when trying to model even simple cases like dilute solutions using Henry’s and Roult’s law, especially if we deal with multicomponent systems and multiple defects[20].

2.1.7The origin of the Gibbs Energy

Based of physical models one can calculate contributions to the Gibbs energy due to electrons, phonons, magnetism etc. In CT this separation is not considered except for the simple model for ferromagnetic transition. The basic reason is that it requires much more data to model each contribution rather than the integral Gibbs energy and such data are simply not available for multicomponent systems. Additionally the calculations using CT databases are used for engineering purposes and values of transformation temperatures and solubilities are needed with a higher accuracy than provided by the results from first principles calculations. But as will be explained in the next section such data can be used in the same way as experimental data to fit model parameters.

2.2The assessment of model parameters

In order to calculate any thermodynamic properties for a system one must have a software which can minimize the appropriate thermodynamic function and a database with assessed model parameters.

The pure elements in the most imporatnt phases like FCC, BCC, HCP, liquid can be found in the SGTE pure element database[14]. For each binary system the model parameters for the stable phases must be determined by fitting model parameters for the different phases to the available experimental and theoretical data.

The assessment of a binary system is a scientific task which includes collecting all available data, possibly adding also own experimental results, both for themodynamics like chemical potentials, heat capacities, heats of mixing and formation as well as phase diagram data like solubilities, temperatures of transformations etc.

The models for the phases must be selected based on crystallographic information, with which the model parameters vary. All data are introduced to a software like PARROT[21]

in the Thermo-Calc software and a least square method is used to minimize

(17)

As the experimental data are usually scattered and incomplete several attempts with different models, model parameters, weights must be tried to obtain a satisfactory agreement, also in regions with no experimental data. One must also take into account that the phases are modelled for a much larger temperature and composition range than there is experimental data available. If only a limiting value of an experimental property is known, for example a solubility, it is possible to use inequality constraints in an assessment forcing the calculated value of the property to be less or larger than the experimental value.

In Fig. 1 an assessment of the Al-Fe system by Sundman et al.[22]shows several diagrams calculated from the models and compared to different kinds of experimental data. A 4 sublattice CEF model was used for the bcc phase making it possible to describe both the B2 and D03ordering. An assessment always requires a judgement of the importance of many different kinds of data and the limitations of the models.

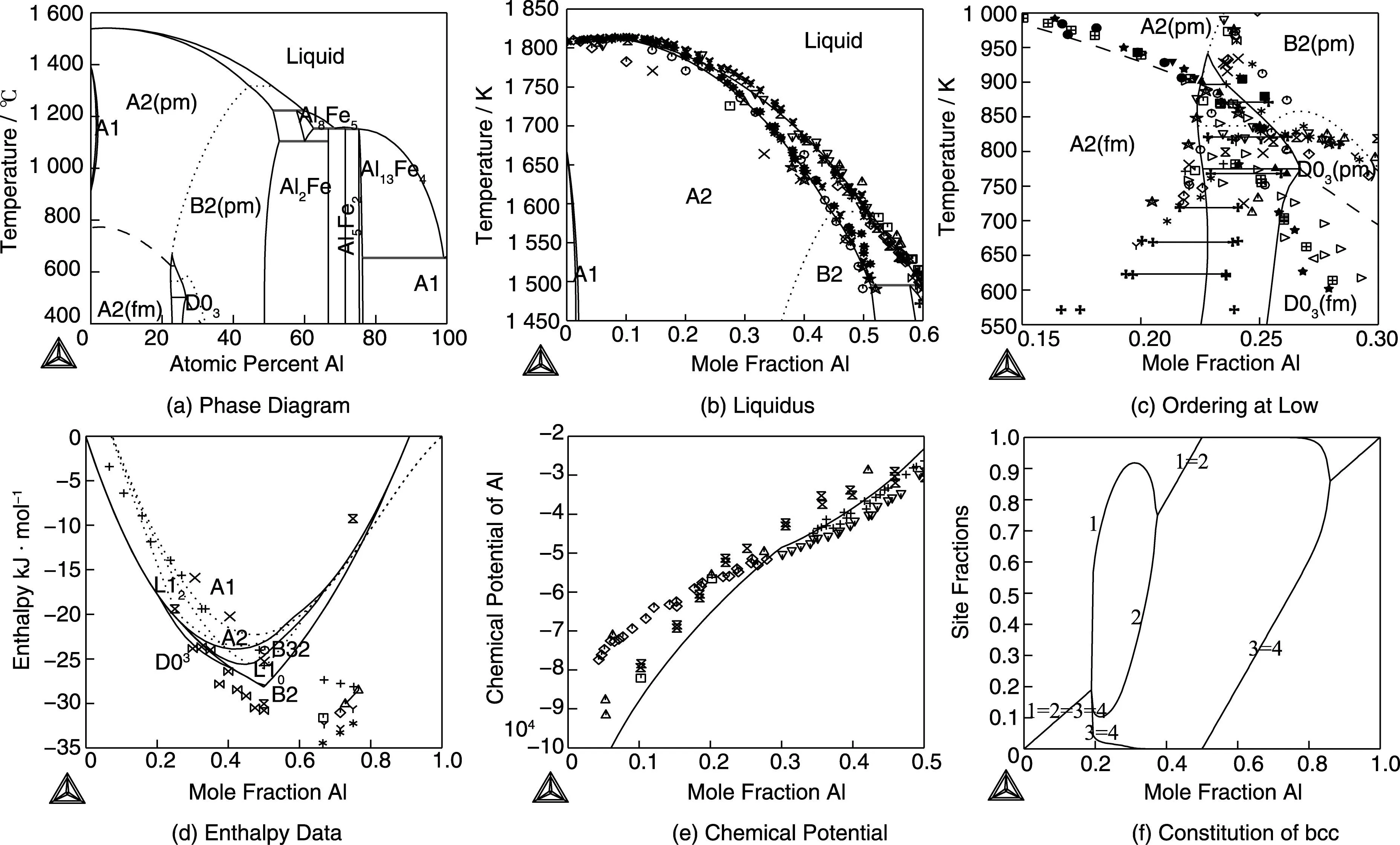
Fig.1　The Al-Fe phase diagram in (a) from an assessment by Sundman et al.[22]together with diagrams showing the fit to various experimental data, in (b) the liquidus on the Fe-rich side, in (c) at low temperature on the Fe-rich side where ferromagnetic and chemical ordering have a complex interaction with first and second order transitions, in (d) the enthalpies of the different phases at 298.15 K relative to bcc Fe and fcc Al, in (e) the chemical potential of Al at 1 273 K on the Fe-rich side and in (e) the constituent fractions of Al on the different sublattices in bcc at 300 K across the whole composition range, above 50% Al the bcc is metastable

The different ordered bcc structures are shown in Fig. 2. These require a 4 sublattice model and even if some of these are important only in ternary systems they must be assessed already in the binary.

Recently the development of software like VASP[23], Quantum espresso[24], abinit[25]and others have made it possible also to use theoretical data based on Density Functional Theory (DFT). Such data are particularly useful to model the Gibbs energy in the metastable regions of the phases where there are no experimental data.

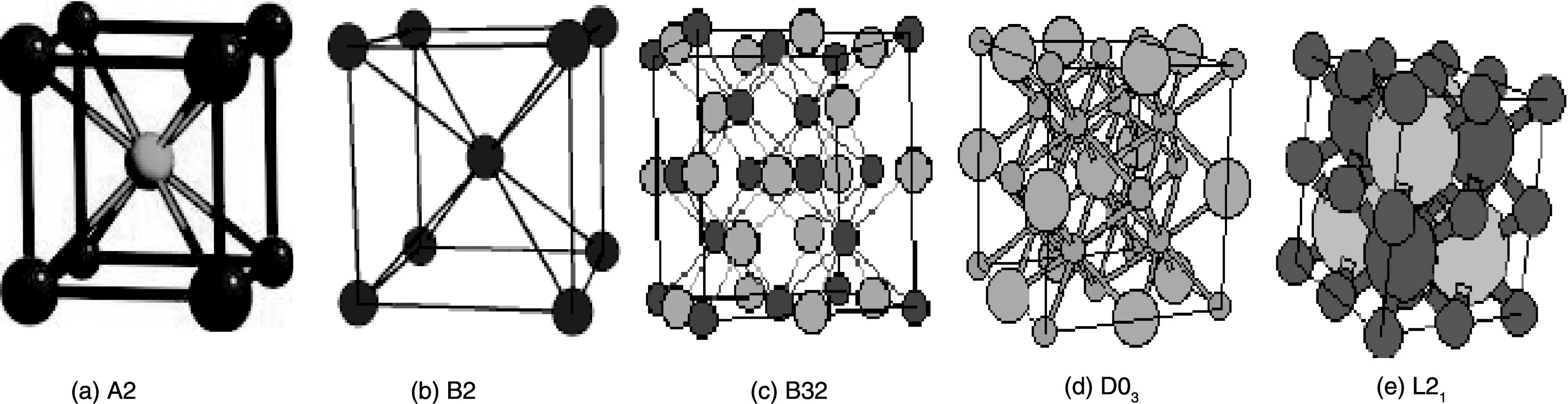
Fig.2　The bcc structure of A2, together with the ordered B2, B32, D03 and L21 structures

An assessment can typically take 3~9 months and several assessments are published every year in journals like Calphad, Journal of Phase Equilibria and Diffusion, Intermetallics, Acta Materialia, Metallurgical Transactions etc. At present more than 500 assessments of binary systems have been published which give accurate description of the experimental data. Several assessments of ternary and a few higher order systems are also published regularly.

2.3Thermodynamic databases

Thermodynamic databases are based on the combination of published assessments provided the assessments have used the same descriptions of the pure elements and the same models for the solution phases. This technique of combining independent assessments is a key issue of the CT technique and influences the work on each individual assessment. In particular the description of the metastable ranges of a phase in a binary system is important for modelling extrapolations of this phase in a ternary or higher order system.

The development and the maintenance of thermodynamic databases require skilled and experienced scientists combining data from several assessments and determining reasonable extrapolations of solution phases in multicomponent systems, where little or no data are available.

2.3.1Databases for industrial applications

Software companies with tools for equilibrium calculations[1-4]also provide thermodynamic databases. These databases are regularly extended, updated and corrected with new available data. The databases are normally centered around an element like Fe for steel databases, Ni for superalloys, Al for aluminium alloys etc. The databases have usually a limited range for alloy additions and inside these limits the results of an calculation will be within the error limits of an experimental determination. As a calculation takes a few seconds whereas the experimental work may take several months the gain is obvious, also if the cost of the database and software is high. Especially in planning experimental work on new alloys the use of calculations is very cost effective. In order to select a database one can usually have some calculations made for the alloys of interest to determine how well it can reproduce already known data. It is not obvious that the largest, or most expensive, database is the best.

2.3.2Databases for teaching and academic research

For teaching and research it is usually possible to obtain software and subsets of the commercial database for little or no cost from most vendors. It is important that students are made aware of these computational facilities before they start their work. For example Thermo-Calc has a free version for ternary systems[26]. At the same website there are also examples teaching thermodynamics using software.

2.3.3Future databases

One problem with thermodynamic databases is the “inertia” they represent. For example if one wants to change the description of a pure element as new data become available one must reassess or at least check all systems where this element appears and possibly modify other parameters to reproduce the experimental data in higher order systems. The same problem occurs if one wants to change the model for a phase, all systems where this phase is present must be changed. In many cases this will require completely new assessments.

The development of the current databases and software started more than 15~20 years ago when computers were much more limited. Even if these has been extended and improved continuously,there is an urgent need to improve the modelling, databases and software to take advantage of the development of computer hardware and software and meet the need of a demanding materials science community. This stated, a large part of this community is not yet aware of the accurate calculations possible already by the current software and databases. Extending the usage of the already available facilities will hopefully provide incentive and funding for starting an improved should be modelling and database development.

In the future, it could be of interest to establish a thermodynamic database, which can be used for several different alloy systems, such as Al alloys, Mg alloys, and Ni-based superalloys. Such an attempt has been made by Du and co-workers[27], who have established the thermodynamic descriptions for many important systems over the whole composition and temperatures via a hybrid approach of key experiment, first-principles calculation and CALPHAD modeling. These descriptions over the wide composition and temperatures can be used as the nucleus of such general thermodynamic databases.

3The calculation of multicomponent equilibria

In the Calphad technique each phase is modelled separately taking into account its particular properties. In almost all cases models for the Gibbs energy are used for the minimization as most thermodynamic databases describe this as a function of T,P and amount of components, NA, where A is a component. In most cases the components are the same as the elements in the periodic chart.

There are basically two methods to handle multicomponent system with several phases. One is equating the chemical potentials in the stable phases and this is described in a recent paper by Piro et al.[28].

The other method uses a Lagrangian method to minimize the total Gibbs energy with various types of constraints. This is used in ChemSage, based on the paper by Eriksson[29]and in Thermo-Calc based on the paper by Hillert[30]and the thesis by Jansson[21]. It is also used in a software developed by Lukas[31]and it has recently been adopted in an open source software called Open Calphad[32, 33]. As this is freely available it will be used to describe the method.

3.1The Gibbs energy

The Gibbs energy, G, is an extensive property and can be subdivided in many different ways. One well known formula relates the Gibbs energy to the chemical potentials, μA, and the numbers of moles of the elements, NA:

(18)

The definition of the chemical potential is given in eq. 13. We can also divide the Gibbs energy on the set of stable phases in the system:

(19)

The differential of the Gibbs energy when there are several phases is:

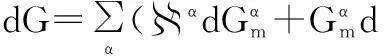
(20)

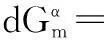
(21)

3.2Minimization with constraints

To minimize a function with constraints we apply a Lagarangian equation where each of the equality constraints has a multiplier. When the constraint is obeyed the minimum of the Lagrangian is the same as the original function. The multipliers can be used to find the method to vary the variables to fulfill the constraints.

The variables in the Gibbs energy expression have several constraints. The first is that the sum of the site fractions on each sublattice is unity:

(22)

For a closed system we have the constraint on the amount of elements

(23)

We can also add constraints on the volume, and prescribe that a phase should be stable or that a chemical potential or activity is known.

To minimize the Gibbs energy of a system with constraints we can use a Lagrangian as

(24)

For the partial derivative of L with respect to the amount of a stable phase α we get:

(25)

and from this equation we can understand that the Lagrangian multiplier μAis the chemical potential of element A.

For an unstable phase ψ which is not included in the stable phase set, i.e.α=0 we get:

(26)

and the driving force, γψ, for an unstable phase can be calculated as part of the minimization. If γψbecomes positive it means that the phase ψ should be added to the stable phase set. If the amount for a stable phase α,α, becomes negative it means this phase has become unstable and should be removed from the stable set. In both cases we must change the set of stable phases which must be made with some care.

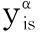
(27)

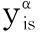
(28)

But we cannot calculate these changes now, because we must first solve how the potentials T,P and μAdepend on the external conditions imposed for the equilibrium calculation by the user which is done in a separate step as described by Hillert[30].

With access to a thermodynamic software and an appropriate database for the system of interest we can make many types of calculations. In principle each calculation represents a possible experiment but from the calculation one can obtain much more information than from a single experiment. Not only the amount of the stable phases and their constitution (constituent fractions) as well as composition (mole fractions) but also the chemical potentials and the heat capacity.

3.3Conditions for a calculation

Most software allow very flexible set of conditions for a calculation like specifying a chemical potential rather than the amount of a component or to find directly the temperature (or composition) when a specific phase becomes stable, for example the liquid. In some cases the volume rather than the pressure is known and in some cases it is important to calculate the heat of a transformation from an initial to a final state. All this is very useful for planning various experimental or processing routes.

It is also easy to calculate metastable equilibria by suspending one or more of the stable phases. This can be useful to show what is the state of a material that is quenched or when some phases are slow to nucleate and grow to their equilibrium amount, the most useful phase diagram for Fe-C with cementite can only be calculated by suspending the graphite as cementite is not the most stable phase. This will be further discussed later when we describe how thermodynamic and kinetic data can be used to simulate phase transformations.

3.4Property diagrams

The most frequent use of calculations are to generate diagrams to show how the system varies with various properties, for example when changing the temperature or composition of a system. The simplest types of such diagrams are generated varying just one condition and plotting how the other properties varies with this and is known as a property diagram.

To generate a property diagram we first set conditions for a single equilibrium calculation and then select one of these to vary between a minimum to a maximum value. In Fig.3 some examples of such diagrams are shown, calculated using the SGTE solution database[34]. Note that it is possible to plot several properties from a single calculation. Several of the diagrams in Fig.1 are also propertydiagrams.

Fig.3　Property diagrams for a SAF2507 high corrosion resistant duplex stainless steel containing Cr, Ni, Mo and N, in (a) the amount of phases as function of T, in (b) at 1 350 K to determine the correct amount of N to have the duplex structure, in (c) the PRE numbers for the ferrite and austenit phases are plotted as function of the amount of N at 1 350 K. The PRE is an empirical formula for the corrosion resistance which depends on the composition

3.5Phase diagrams

Phase diagrams are maps showing regions with different sets of stable phases. Many scientists are familiar with binary diagrams but often feel uncertain how to interpret ternary or multicomponent phase diagrams because they have never come across them while learning materials science and many features in binary diagrams are not present when one has more than two components. However, CT gives access to thermodynamic software and databases and makes it easy to calculate multicomponent phase diagram as well as many related diagrams with properties useful for understanding and developing new materials.

3.5.1Binary phase diagrams

Most information for binary phase diagram comes from experimental data and there are several handbooks of drawn phase diagrams like Massalsky[35]. But the phase diagram information together with thermodynamic data can be used in the assessment procedure to generate thermodynamic model parameters as shown in Fig.1 for the Al-Fe system. This means that from a calculated phase diagram one can obtain much more information than just the solubilities and transformation temperatures. Some calculated phase diagrams for the Al-Ni, O-U and Ti-C systems are shown in Fig.4 taken from the Thermo-Calc Ni-superalloy database[40], an assessment by Guéneau[36]and the SGTE solution database[34]respectively.

3.5.2Multicomponent phase diagrams

The main difference between binary and multicomponent phase diagrams is that the lines in such a multicomponent phase diagram only separate regions with different sets of stable phases. This is in contrary to binary diagrams where the lines are also solubility lines, giving the composition of one of the phases. This may be more clear if we call the lines in a phase diagram “Zero Phase Fraction” (ZPF) lines following a suggestion by Morral[37]. This means that the lines have less information and for example in a region with 5 phases stable the phase diagram does not provide any information about the amount of the phases or their composition. Such a diagram would not be very useful if the lines were just drawn but as they are calculated from a thermodynamic database one can easily make a single equilibrium calculation at any point and obtain detailed information about the amounts and compositions of the phases, chemical potentials and much more. In Fig.5 some multicomponent phase diagrams are shown.

Fig.4　Examples of calculated binary phase diagrams for Al-Ni(a), O-U (b) and C-Ti

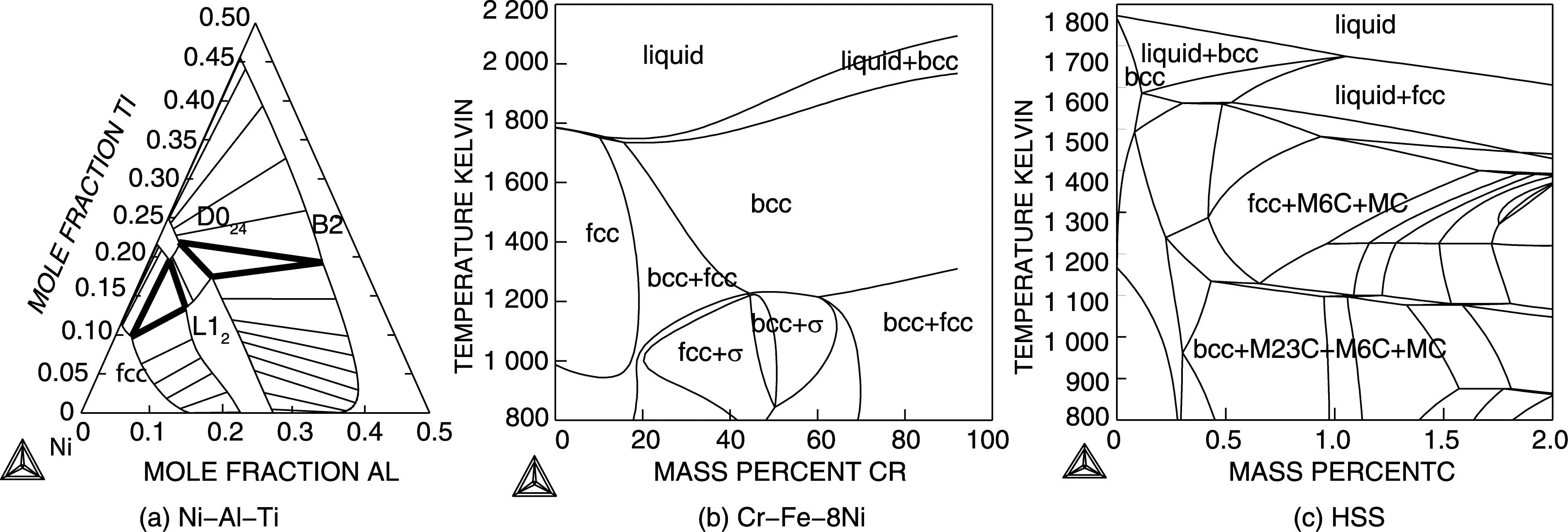
Fig.5　Examples of multicomponent phase diagrams. In an isothermal section of the Ni-rich corner of the Al-Ni-Ti system with the ordered L12 , D024 and B2 phases (a). In the two-phase regions the tie-lines indicate the composition of the phases in equilibrium. Calculated using[40]. In an isopleth section of a steel with 8 mass% Ni and varying Cr content (b). The lines separate regions with different sets of stable phases. There are no tie-lines in such a section but detailed information of the phase amounts and compositions can easily be calculated. Calculated using [34]. In an isopleth section for a high speed steel (HSS) with 4.5 mass% Cr, 8 mass% Mo, 1mass% V, 0.3 mass% Si and varying amount of C and Fe (c). The phases stable in some regions are indicated. Calculated using[34].

3.6Calculations useful for simulations of phase transformations

Finally, as already mentioned the modelling of the phases in each system also include metastable ranges of the phases as shown in the assessment of the Al-Fe system. This may seem an unnecessary effort but turns out to be one of the most useful features of the modelling because this makes it possible to estimate the driving forces for nucleation of new phases. Consider the Fe-Mo system from an assessment of Guillermet[38]with the phase diagram shown in Fig.6a.

If we start with an alloy with 20 mole% Mo at 1 700 K this will be single phase bcc. Rapidly quenching this alloy to 1 400 K we come into the two-phase region with bcc and the phase. In order to demonstrate how we can simulate the nucleation and growth of this phase we calculate the Gibbs energy curves at 1 400 K as shown in Fig.6b-h. In Fig.6b (and 6c which is just a magnification) a tangent is drawn to the Gibbs energy curve at the initial composition of the bcc phase (marked by a verticalt dashed line). This bcc is metastable because there are several Gibbs energy curves that are below this tangent and the system can decrease its energy by precipitating any of these. In Fig.6d the final state is shown by a common tangent between theμphase and a bcc phase with lower Mo content. But to find the driving force to precipitate theμphase, we must make a parallel tangent construction as shown in Fig.6d. This also gives the composition of the phase that will precipitate. In Fig.6f the parallel tangents for the other intermetallic phases are shown indicating that theμphase has the largest driving force. After nucleation the μ phase will grow by diffusion in the bcc phase. There will also be a small adjustment of the initial composition of the μ phase during growth to obtain the finalcommon tangent shown in Fig.6g (magnified in Fig, 6h). During the growth process the slope of the Gibbs energy curve for bcc, i.e. the chemical potential, drives the diffusion.

Solidification of alloys is another important case when thermodynamic data are useful for simulating a phase transformation. During normal solidification the diffusion in the

solid phase is too slow to maintain a homogeneous composition. In the liquid on the other hand there is convection which can more rapidly ensure it is homogeneous. This has lead to the so called Gulliver-Scheil solidification model which can be easily implemented in a thermodynamic software[39], also allowing for some elements, like interstitials, to maintain equilibrium composition in both liquid and solids. With access to thermodynamic databases one can easily calculate the equilibrium at the solid/liquid interface at varying temperature. After each step in temperature the solid phase formed is removed and a new equilibrium is calculated using the new liquid composition. This simulation can continue, and handle both eutectic and peritectic reactions, until there is an invariant reaction when the last liquid disappears. The advantage with this model is that it does not require any kinetic data and the simulation can be calculated as rapidly as a phase diagram.

Fig.6　These figures show the phase diagram for Fe-Mo in (a) and in (b) to (h) the Gibbs energy curves at 1 400 K for this system together with tangent constructions to show how these data can be used to simulate the transformation of a metastable bcc

4Role of computational thermodynamics in kinetic simulations of phase transformations in materials science

As stated above, computational thermodynamics are very useful for some phase transformation simulations. However, time cannot be considered, and the addition of kinetic information is required. In this case, kinetic simulation tools, such as the one-dimensional (1-D) DICTRA[5]and TC-PRISMA[41]simulations, two-or three-dimensional (2-or 3-D) phase-field modeling, are needed.

Actually, since the first introduction of reliable thermodynamic databases almost three decades ago, the importance of thermodynamic and kinetic simulations for the computational aided material design is ever growing[42], especially with large acceptance of thermodynamic and kinetic software packages in the industry[43]. The computer aided design of materials has the ability to simulate, predict and optimize alloy composition and materials processes to a quantitative degree. The core for quantitative kinetic simulations is the input of reliable thermodynamic and kinetic databases. The reliable thermodynamic databases can provide accurate diffusion potentials, the gradient of which truly drives the diffusion, and the thermodynamic factor, which helps to calculate interdiffusion coefficients together with atomic mobilities. While the kinetic databases, or the so-called atomic mobility databases, can provide reliable atomic mobilities, from which all kinds of composition-and temperature-dependent diffusion coefficients can be computed together with the thermodynamic databases.

4.1Diffusion coefficients and atomic mobility

The effect of long-range diffusion in a multicomponent system in a single phase is well described by Onsager’s law[44]and the rate of change of the concentration of element i, cican be written as

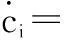
(29)

(30)

(31)

where Gmis the Gibbs energy per mole formula unit, as defined in Section 2. The mole fraction xishould be an easier property to handle thermodynamically than cias the volume V may depend on T and P. With Eq.30, we can transfer Eq.29 into

(32)

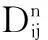
(33)

(34)

with the Kronecker delta δki.

4.2The diffusion potential

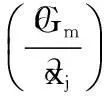
(35)

using the definition of the chemical potential from Section 2.1.5.

A graphical representation of the diffusion potentials for the C-Cr-Fe-Mn system is visualized in Fig.7 and Fig.8. Thermodynamic descriptions for fcc and bcc phases in the C-Cr-Fe-Mn system are directly taken from thermodynamic database established by Lee[46]. Here, Fe is chosen as the reference element.

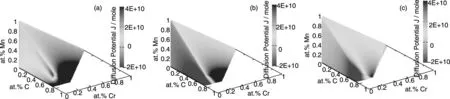
Fig.7　 Diffusion potential for the ferrite with iron as the reference element at 923 K:(a) Carbon,(b) Chromium,(c) Manganese

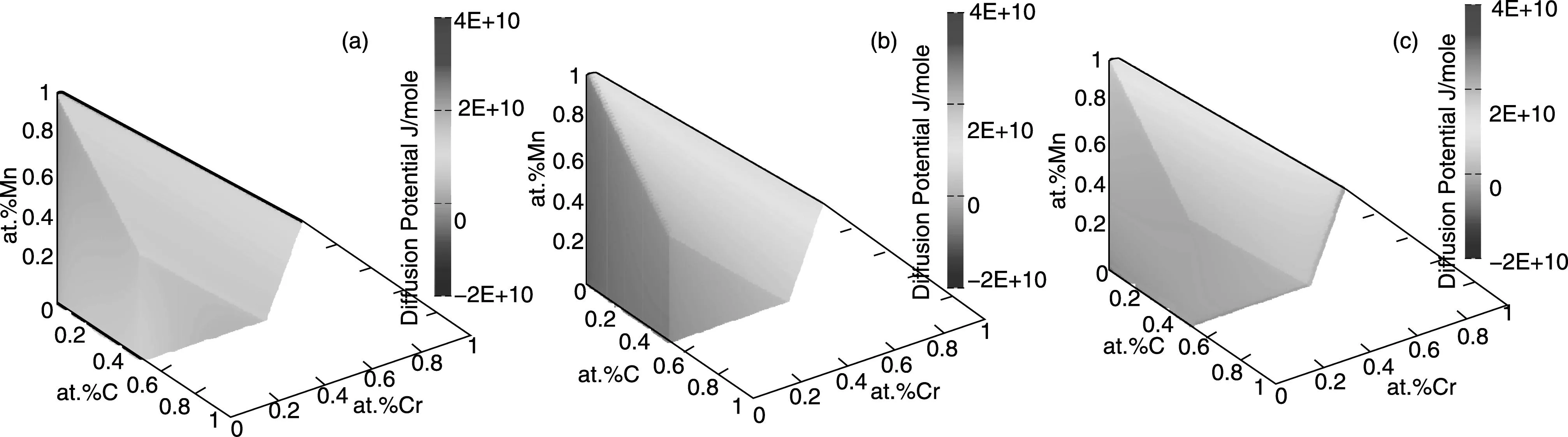
Fig.8　Diffusion potential for austenite with iron as the reference element at 923 K:(a) Carbon,(b) Chromium,(c) Manganese

4.3DICTRA simulations

In order to perform kinetic simulation for diffusion-controlled phase transformations in multicomponent systems, the DICTRA software package has been developed and operates under the CALPHAD framework. Based on the sharp interface and local equilibrium hypothesis, DICTRA has been successfully utilized to simulate various phase transformation processes with the high-quality thermodynamic and atomic mobility databases. Example applications include heat treatment, microsegregation during solidification, growth and dissolution of precipitates, coarsening and more, which are all important considerations for the development of novel materials[5].

Cemented carbides play key roles in the production of hard and tough tool materials, which are used in high wear environments, such as cutting, machining and mining applications. The formation of the gradient structure in multicomponent cemented carbides at liquid phase sintering temperature is a diffusion-controlled process, which is mainly controlled by alloy compositions, sintering temperature, time, atmosphere and so on. Knowledge of both thermodynamics and diffusivity is indispensable to understand formation mechanism, optimize technological parameters and design new type of graded cemented carbides. A cemented carbide WC-Ti(C,N)-(Ta,Nb)C-Co is sintered under vacuum at 1 450 ℃ for 1 h[47]. Figure 9 shows SEM micrograph of the cross section of the cemented carbides. In the micrograph, bright contrast is WC phase, grey is cubic phase, and dark is Co-rich binder phase. It is obvious that the near-surface of the alloy has formed the gradient zone which is enriched in binder phase and depleted in cubic carbides. Based on the thermodynamic and diffusion databases, the gradient zone formation of the cemented carbides is simulated by DICTRA software, and compared with the experimental results. Figure 10 illustrates the experimental and simulated elemental concentration profiles for Ti, Ta, Nb and Co in the cemented carbides[47]. As can be seen in the figure, the simulated results are in good accordance with the experimental data.

Fig.9　SEM micrograph of the cross section of the cemented carbides after sintering in vacuum conditions at 1 450 ℃ for 1 h[47]

Fig.10　Calculated elemental concentration profiles for Co (a),Ta (b),Ti (c),Nb (d) in the cemented carbides after sintering for 1 h at 1 450 ℃ in a N-free atmosphere, as compared with the experimental data[47]

4.4PRISMA simulations

TC-PRISMA is a newly released computational tool for the simulation of precipitation reactions in multicomponent alloys from the Thermo-Calc company in Sweden. With data for interfacial energy, volume, and elastic modulus in addition to the available thermodynamic and kinetic data, TC-PRISMA can be used to simulate the concurrent nucleation, growth, and coarsening of precipitate phases in multicomponent aluminum alloys. This new computational tool is based on the Langer-Schwartz theory[48]and adopts the Kampmann-Wagner numerical approach[49]to solve the governing equation for the evolution of particle size distribution function. A general growth rate model[50]for precipitate particles in multicomponent systems has been developed and implemented. With this software, variations with time of mean radius, number density, volume fraction, and size distribution of precipitate particles can be simulated. Nucleation rate and precipitate composition can also be obtained during the simulation. Coupled with relevant microstructure-property models, the computer program could be used to estimate the change of mechanical properties of alloys upon aging hardening treatment.

One nice example is from Zhang et al.[51]and presented in Fig.11. Watanabe et al.[52]have measured the size evolution for Al3Sc precipitates in an Al-1wt.%Mg-0.27wt.%Sc alloy at 4 different temperatures. In Figure 11, a comparison has been made between the calculated mean radius, using TC-PRISMA, and their measured values. As can be seen, the simulation results agree with the measurements extremely well[51].

4.5Phase-field modeling

Phase-field models were introduced to materials science when Kobayashi et al. in 1993[53]succeeded with the modelling of dendritic growth in an undercooled melt. After more than 20 years’ development, the phase-field approach has emerged as the method of choice to simulate microstructural evolution in

Fig.11　Calculated mean radius of precipitates in an alloy at different temperatures compared with experimental information from Watanabe et al[52]

various materials processes during their lifetime and service. Two widely recognized advantages of this approach are: (i) the diffuse interface, with which the explicit tracking of the phase boundaries during complex phase transformations can be avoided and (ii) the description of non-equilibrium states in general.

A special class of phase-field models are the so-called multi-phase-field (MPF) models, initially proposed by Steinbach et al.[54], with additions by Tiaden et al.[55], Steinbach and Apel[56], and Eiken et al.[57]. All these forms the basis of the first commercial software package for phase-field simulation, i.e. MICRESS (MICRostructure Evolution Simulation Software)[58].

Moreover, the coupling to the CALPHAD thermodynamic and atomic mobility databases has become a good standard nowadays for providing reasonable thermodynamic information needed in the phase-field models. For MICRESS, the strategy is to run a CALPHAD software package in parallel to the phase-field simulation via an interface, named TQ.

Very recently, a phase-field model with finite interface dissipation was developed by Steinbach et al.[59]and Zhang and Steinbach[60]in the framework of the MPF formalism. This approach provides the description of various kinetic processes at the mesoscopic scale without restriction to the type of transformation ranging from the chemical equilibrium to strongly non-equilibrium phase transformations. The novel feature of the model is that each phase concentration is assigned by a kinetic equation to account for finite interface dissipation instead of applying an extra condition for solute partitioning between the phases as in traditional models: the condition of a given partitioning[55, 61]or the condition of equal diffusion potentials[57]. With such a novel feature, the external equilibrium calculation for the partitioning at the interface can be avoided in phase-field simulations. The thermodynamic potentials can be thus directly incorporated from a CALPHAD thermodynamic database[60, 62]. This new phase-field model and its unique coupling techniques have been incorporated into an open source phase-field code, named as “Open Phase”[63].

In multi-phase steels, the different solubilities of the phases for the different elements lead to a complex diffusion and

redistribution behaviour. These redistribution processes, grain size and growth can determine the processing time and temperature for heat treatment. Careful diffusion simulation can reduce the amount of necessary experiments. By coupling with the CALPHAD-type databases, the diffuse-interface phase-field simulation can nicely solve this problem. Starting from an off-equilibrium simulation after casting caused by segregation processes, depletion or precipitation, the sample containing ferrite and austenite phases is simulated at temperatures up to 900 K. The diffusion and redistribution is shown in Fig.12 for a simulation sample size of only 256 μm after 0, 6 and 54 seconds. Moreover, the equilibrium state calculated with thethermodynamic software package Thermo-Calc is also superimposed. The thermodynamic database is also from[46]. As can be seen, the supersaturation of carbon in ferrite is decreasing over time, accompanied with a phase growth of the ferrite phase.

Here, one more example about a dual-phase Cr-Mn steel is presented for the phase-field simulation, as presented in Figs.13 to 15. The chemical energy density fchemcan be calculated using the same database as stated above[46],which is

Fig.12　Diffusion in the C-Cr-Fe-Mn system with a phase on the left and a phase on the right side of the simulation domain. Diffusion profiles are plotted for Carbon (black), Manganese (dark grey) and Chromium (light gray) at 0, 6 and 54 seconds. The diffusion simulation is performed using OpenPhase, while the equilibrium state is calculated using Thermo-Calc

Fig.13　Gibbs energy in the C-Cr-Fe-Mn system at 923 K:(a) austenite,(b) ferrite

visualized in Fig.13. The energy information can further be used for a phase-field simulation of a dual-phase material of Cr-Mn steel, shown in Figs.14 and 15. These simulations help to adjust the heat treatment process or alloying parameters to efficiently increase overall material properties.

Fig.14　Initial state of the 2D phase field simulation, highlighting the two phases. Each phase is separated into three individual grains

Fig.15　Visualization of the Carbon and Manganese concentration at different time steps:(a) Carbon at.% at 0s,(b) Carbon at.%at 60s,(c) Mn at.% at 0s,(d) Mn at.% at 60s

5Conclusions

Software and databases to calculate phase equilibria and phase diagrams and to simulate phase transformations are indispensable tools in materials science. Recently initiatives to provide open source software have been taken, such as Open Calphad[32, 33]and Open Phase[63]. These are still in a development stage but some of the diagrams in this paper have been calculated with them. The commercial software vendors have databases for many different types of alloys like steels, superalloys, aluminium alloys, slags etc. with up to 20 elements and the work to develop open source databases have only just begun.

Using thermodynamic and kinetic software and consistent databases to develop new materials will give more reliable results than taking data from different sources and reduce the time and cost. Experimental work can be greatly reduced by selecting the experimental compositions and processes based on the results of calculations and simulations.

Acknowledgements One of the authors (Bo Sundman) acknowledges the distinguished professor program released by ministry of education of China and the State Administration of Foreign Experts Affairs of China and a senior research award from the Humboldt Foundation in Germany.The authors appreciate Ms. Jingjing Zhou and Ms. Juan Chen from State Key Laboratory of Powder Metallurgy, Central South University for their kind help on translating the format from latex into word.

References

[1]Bale C W, Bélile E, Chartarnd P,etal.Thermochemical Software and Databases-Recent Developments[J].Calphad, 2009(33): 295-311.

[2]Chen S L, Daniel S, Zhang F,etal. The PANDAT Software Package and Its Applications Original Research Article[J].Calphad, 2002(26): 175-188.

[3]Davis R H, Dinsdale A T, Gisby J A,etal. MTDATA-Thermodynamic and Phase Equilibrium Software from the National Physical Laboratory[J].Calphad, 2002(26): 229-271.

[4]Andersson J O, Helander T, Höglund L,etal. Thermo-Calc & DICTRA, Computational Tools for Materials Science[J].Calphad, 2002(26): 273-321.

[5]Borgenstam A, Höglund L, Ågren J,etal. DICTRA, a Tool for Simulation of Diffusional Transformations in Alloys[J].JournalofPhaseEquilib, 2000(21): 269-280.

[6]Chen L Q. Phase-Field Models for Microstructure Evolution[J].AnnualReviewofMaterialsResearch, 2002(32): 113-140.

[7]Moelans N, Blanpain B, Wollants P. An Introduction to Phase-Field Modeling of Microstructure Evolution[J].Calphad, 2008(32): 268-294.

[8]Steinbach I. Phase-Field Models in Materials Science[J].ModellingandSimulationinMaterialsScienceandEngineering, 2009(17): 073001-31.

[9]Lukas H L, Fries S G, Sundman B.ComputationalThermodynamics[M]. Cambridge Univ Press, 2007.

[10]Hickel T, Kattner U R, Fries S G. Computational Thermodynamics: Recent Developments and Future Potential and Prospects[J].PhysicaStatusSolidiB, 2014(251): 9-13.

[11]Inden G. The Role of Magnetism in the Calculation of Phase Diagrams[J].PhysicaB+C, 1981(103): 82-100.

[12]Kaufman L, Bernstein H.ComputerCalculationsofPhaseDiagrams[M].New York Academic Press,1970.

[13]Dinsdale A T. SGTE Data for Pure Elements[J].Calphad, 1991(15): 317-425.

[14]SGTE. http://www.sgte.org.

[15]Hillert M. The Compound Energy Formalism[J].JournalofAlloysandCompounds, 2001(320): 161-176.

[16]Sluiter M H F. Ab Initio Lattice Stabilities of Some Elemental Complex Structures[J].Calphad, 2006(30): 357-366.

[17]Sundman B, Fries S G, Oates W A. A Thermodynamic Assessment of the Au-Cu System[J].Calphad, 1998(22): 335-354.

[18]Sundman B, Ågren J. A Regular Solution Model for Phases with Several Components and Sublattices, Suitable for Computer Applications[J].JournalofPhysicsandChemistryofSolids, 1981(42): 297-301.

[19]Rogal J, Divinski S V, Finnis M W,etal. Perspectives on Point Defect Thermodynamics[J].Phys.StatusSolidiB, 2014(251): 97-129.

[20]Sundman B, Guéneau C, Dupin N. Modeling Multiple Defects in Ionic Phases like UO2±X Using the Compound Energy Formalism[J].ActaMaterialia, 2011(59): 6039-6047.

[21]Jansson B. Thesis, 1984 Department of Physical Metallurgy, Royal Institute of Technology, Stockholm, Sweden.

[22]Sundman B, Ohnuma I, Dupin N,etal. An Assessment of the Entire Al-Fe System including D03 Ordering[J].ActaMaterialia, 2009(57): 2896-2908.

[23]http://www.vasp.at.

[24]http://www.quantum-espresso.org.

[25]http://www.abinit.org.

[26]Free Version of Thermo-Calc: http://www.thermocalc.com/academia .

[27]Du Y, Liu S H, Zhang L J,etal. An Overview on Phase Equilibria and Thermodynamic Modeling in Multicomponent Al Alloys: Focusing on the Al-Cu-Fe-Mg-Mn-Ni-Si-Zn System[J].Calphad, 2011(35): 427-445.

[28]Piro M H A, Simunovic S, Besman T M,etal. The Thermochemistry Library Thermochimica[J].ComputationalMaterialsScience, 2013(67): 266-272.

[29]Eriksson G. Thermodynamic Studies of High Temperature Equilibria. III. SOLGAS, a Computer Program for Calculating the Composition and Heat Condition of an Equilibrium Mixture[J].ActaChemicaScandinavica, 1971(25): 2 651-2 658.

[30]Hillert M. Some Viewpoints on the Use of A Computer for Calculating Phase Diagrams[J].PhysicaB+C, 1981(103): 31-40.

[31]Lukas H L, Weiss J, Henig E Th. Straegies for the Calculation of Phase Diagrams[J].Calphad, 1982(6): 229-251.

[32]Sundman B, Palumbo M, Kattner U R, Fries S G.JournalofIntegratingMaterialsandManufacuringInnovation, DOI: 10.1186/s40192-014-0029-1.

[33]http://www.opencalphad.org or the opencalphad repository at http://github.com.

[34]SGTE Solution Database, (2002) http://www.thermocalc.com.

[35]Massalsky T B (Ed.). Binary Alloy Phase Diagrams, 2nd Ed., ASM International 2007.

[36]Guéneau C, Baichi M, Labroche D,etal. Thermodynamic Assessment of the Uranium-Oxygen System[J].JournalofNuclearMaterials, 2002(304): 161-175.

[37]Gupta H, Morral J E, Novotny H. Constructing Multicomponent Phase Diagrams by Overlapping ZPF Lines[J].ScriptaMetallurgica, 1986(20): 889-894.

[38]Guillermet A F. Straegies for the Calculation of Phase Diagrams[J].Calphad, 1982(6): 127-140.

[39]Chen Q, Sundman B. Computation of Partial Equilibrium Solidification with Complete Interstitial and Negligible Substitutional Solute Back Diffusion[J].MaterialsTransactions, 2002(43): 551-559.

[40]Thermo-Calc Ni-Superalloy Database, 2003 http://www.thermocalc.com.

[41]Chen Q, Sterner G, Jou H J. 1st World Congress on Integrated Computational Materials Engineering, July 10-14 2011, Seven Springs, PA, USA.

[42]Kaufman L. Hume-Rothery and CALPHAD Thermodynamics, CALPHAD and Alloy Thermodynamics, P.E.A. Turchi, A.Gonis and R.D. Shull, TMS, pp. 3-19, 2002.

[43]Olson G B, Kuehmann C J. Materials Genomics: From CALPHAD to Flight [J].ScriptaMaterialia, 2014(70): 25-30.

[44]Onsager L. Reciprocal Relations in Irreversible Processes II.[J].PhysicalReview, 1931(38): 2 265-2 279.

[45]Andersson J O, Ågren J. Models for Numerical Treatment of Multicomponent Diffusion in Simple Phases[J].JournalofAppliedPhysics, 1992(72): 1350.

[46]Lee B J. A Thermodynamic Evaluation of the Fe-Cr-Mn-C System[J].MetallurgicalTransactionsA, 1993(24): 1 017-1 025.

[47]Zhang W B, Du Y, Chen W M,etal. CSUDDCC1-A Diffusion Database for Multicomponent Cemented Carbides [J].InternationalJournalofRefractoryMetalsandHardMaterials, 2014(43): 164-180.

[48]Langer J, Schwartz A. Kinetics of Nucleation in Near-Critical Fluids[J].PhysicalReviewA, 1980(21): 948-958.

[49]Wagner R, Kampmann R. Homogeneous Second Phase Precipitation, in: Materials Science and Technology: A Comprehensive Treatment, ed. P. Haasen (Weinheim, Berlin: Wiley-VCH) 1991, 213.

[50]Chen Q, Jeppsson J, Ågren J. Analytical Treatment of Diffusion During Precipitate Growth in Multicomponent Systems[J].ActaMaterialia, 2008(56): 1 890-1 896.

[51]Zhang L, Markström A, Mason P, Du Y, Liu S, Kjellqvist L, Bratberg J, Chen Q, Engström A. Proceedings of 13th International Conference on Aluminum Alloys (ICAA13), ed. H. Weiland, A.D. Rollett, W.A. Cassada, TMS (The Minerals, Metals & Materials Society), 2012: 305-310.

[52]Watanabe C, Watanabe D, Monzen R. Coarsening Behavior of Al3Sc Precipitates in an Al-Mg-Sc Alloy[J].MaterialsTransactions, 2006(47): 2 285-2 291.

[53]Kobayashi R. Modeling and Numerical Simulations af Dendritic Crystal Growth[J].PhysicaD, 1993(63): 410-423.

[54]Steinbach I, Pezzolla F, Nestler B,etal.A Phase Field Concept for Multiphase Systems [J].PhysicaD, 1996(94): 135-147.

[55]Tiaden J, Nestler B, Diepers H J,etal. The Multiphase-Field Model with an Integrated Concept for Modelling Solute Diffusion[J].PhysicaD, 1998(115): 73-86.

[56]Steinbach I, Apel M. Multi Phase Field Model for Solid State Transformation With Elastic Strain[J].PhysicaD, 2006(217): 153-160.

[57]Eiken J, Botger B, Steinbach I. Multiphase-Field Approach for Multicomponent Alloys with Extrapolation Scheme for Numerical Application[J].PhysicalRevieweE, 2006(73): 066122.

[58]http://web.access.rwth-aachen.de/MICRESS/.

[59]Steinbach I, Zhang L J, Plapp M. Phase-Field Model with Finite Interface Dissipation[J].ActaMaterialia, 2012(60): 2 689-2 701.

[60]Zhang L, Steinbach I. Phase-Field Model with Finite Interface Dissipation: Extension to Multi-Component Multi-Phase Alloys[J].ActaMaterialia, 2012(60): 2 702-2 710.

[61] Karma A. Phase-Field Formulation for Quantitative Modeling of Alloy Solidification[J].PhysicalReview.Letters, 2001(87): 115701.

[62] Zhang L, Stratmann M, Du Y, et al. Incorporating the CALPHAD Sublattice Approach of Ordering into the Phase-Field Model with Finite Interface Sissipation[J].ActaMater, 2014，in press， DOI: 10.1016/j.actamat.2014.11.037.

[63] http://www.openphase.de/.

(编辑：盖少飞惠琼)

Computational Thermodynamics and Its Applicationsto Materials Science

Bo Sundman1, Matthias Stratmann2, Lijun ZHANG3, Yong DU3

(1.INSTN, CEA Saclay, France)

( 2.Interdisciplinary Centre for Advanced Materials (ICAMS), Ruhr University Bochum,Bochum D-44780, Germany )

(3.State Key Laboratory of Powder Metallurgy, Central South University,Changsha 410083, P R China )

Abstract：A short review of the models, databases, software and applications of computational thermodynamics and kinetics in the field of materials science is presented. The most common software is referenced and the most important models for describing the thermodynamic properties of different phases are explained together with the assessment procedure used to obtain model parameters stored in thermodynamic databases. One of the most used algorithm for equilibrium calculation is described and finally some examples of using the software and databases for calculation of equilibria and diagrams as well as the kinetic data for simulations of phase transformations and processes are demonstrated.

Key words:computational thermodynamics; kinetic simulations; phase transformations; Software; databases

DOI:10.7502/j.issn.1674-3962.2015.01.02

Corresponding author：Bo Sundman,Professor,Email:bo.sundman@gmail.com

Received date：2014-12-01

CLC number：TB30Document code： AArticle ID：1674-3962(2015)01-0015-15