混合型开槽同轴布喇格结构的比较研究
2015-02-24丁学用王玲玲吕振肃
丁学用 王玲玲 吕振肃
(三亚学院理工学院,三亚 572022)
混合型开槽同轴布喇格结构的比较研究
丁学用王玲玲吕振肃
(三亚学院理工学院,三亚 572022)
摘要基于电磁仿真软件(Computer Simulation Technology,CST)平台,对几种不同开槽形状同轴布喇格结构的频率响应特性分别进行了数值模拟比较研究.结果表明:三角形开槽带宽最窄而矩形开槽带宽最宽;交替混合型开槽时耦合模式的反射率明显提高,而分半混合型开槽时不仅耦合模式的反射率提高,且其带宽也明显变宽,但两种开槽方式时工作模式的反射率和带宽都位于单一开矩形槽和三角形槽之间;叠加混合型开槽克服了单一矩形槽和三角形槽存在奇点和边界突变的缺点,对模式的选择性能优于矩形开槽,反射率和带宽又大于正弦开槽和三角形开槽,仅其谐振频率点有偏移.这些特点有利于同轴布喇格结构的模式选择、散热和工业生产.
关键词同轴布喇格结构;交替混合型;分半混合型;叠加混合型;反射率
联系人: 丁学用 E-mail:ding2008ding@163.com
引言
由于同轴波导在高功率回旋器件中所展现出的优越特性,基于同轴波导的布喇格结构在光波、集成电路以及微波器件在科技工程界得到广泛应用[1-16],尤其是在回旋自谐振脉塞(Cyclotron Auto-resonance Maser,CARM)、模式耦合以及在毫米、亚毫米波范围内工作的自由电子脉塞(Free Electron Laser, FEL)方面的应用越来越受到人们的关注[3-5].对同轴布喇格结构的研究发现,其周期性边界条件的选频特性所形成的禁带或者通带,可以用来制作反射器、滤波器、模式转换器等器件[3-5].对一段同轴波导的金属内外壁上开周期性单一的矩形和正弦波纹槽的布喇格结构已经有过研究,研究发现两种开槽方式各有其特点[1-2],但从未对开三角形槽进行模拟研究,也没有对三种开槽方式的优缺点以及如何综合利用三种开槽方式的优点而避免其缺点进行比较研究.不同的开槽形状对应于不同的边界条件,导致将有不同的电磁特性.利用三维高频电磁仿真软件CST平台[17],建立仿真模型,将对同轴波导金属内外导体上开矩形槽、三角形槽和正弦槽的同轴布喇格结构以及对混合型开槽同轴布喇格结构的频率响应特性进行数值模拟比较研究,通过比较几种开槽方式的优缺点,以探求最佳的开槽方式,来提高同轴布喇格结构的反射效率和模式选择性能.
1理论模型分析
矩形槽、三角形槽和正弦槽同轴布喇格结构的剖面图分别如图1所示[1-2],基于三种单一开槽形状的同轴布喇格结构,混合型开槽同轴布喇格结构有三种形式:第一种形式其剖面结构如图2(a)所示,矩形和三角形波纹周期性交错开槽,称为交替混合型开槽;第二种形式其剖面结构如图2(b)所示,布喇格结构左半长度是矩形开槽,右半长度是三角形开槽,称为分半混合型开槽;第三种形式其剖面结构如图2(c)所示,称为叠加混合型开槽,其结构由矩形、三角形和正弦形波纹对应点叠加而成.相比之下,由于三角形、矩形开槽是不光滑的间断曲线(从剖面图看),而正弦是光滑的连续曲线,前者在间断点的突变容易导致高频电场击穿,故正弦开槽更具实用性;对比三种单一开槽同轴布喇格结构,交替混合型开槽和分半混合型开槽结构依然存在奇点,边界有突变,而叠加混合型开槽克服了这一缺点.

(a) 矩形开槽
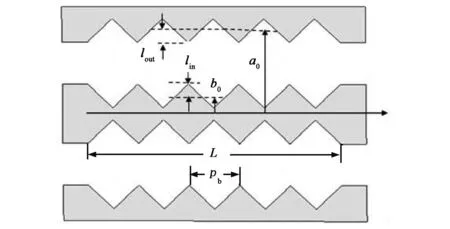
(b) 三角形开槽
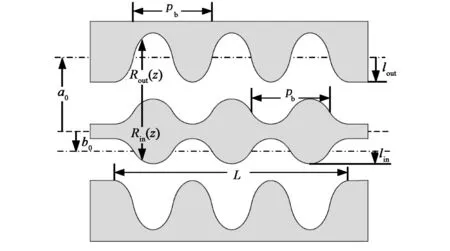
(c) 正弦形开槽图1 同轴布喇格结构剖面图
在图1和图2剖面图的结构中,a0和lout分别为外导体壁的平均半径和开槽波纹深度,b0和lin分别为内导体壁的平均半径和开槽波纹深度,pb为开槽波纹周期,L是结构长度.
由图1和图2可知,三种不同开槽形状的同轴布喇格结构和混合型开槽同轴布喇格结构在纵向上都呈现周期性变化,其中,正弦波纹开槽同轴布喇格结构外壁半径Rout和内导体半径Rin可分别表示成关于纵向位置z变化的函数[12]:
Rout(z)=a0-loutcos(koutz+φout)
(1)
Rin(z)=b0-lincos(kinz+φin)
(2)
式中: kout=2π/pb; kin=2π/pin; φout、pb分别为外导体壁的初始相位和波纹周期; φin、pin分别为内导体壁的初始相位和波纹周期.
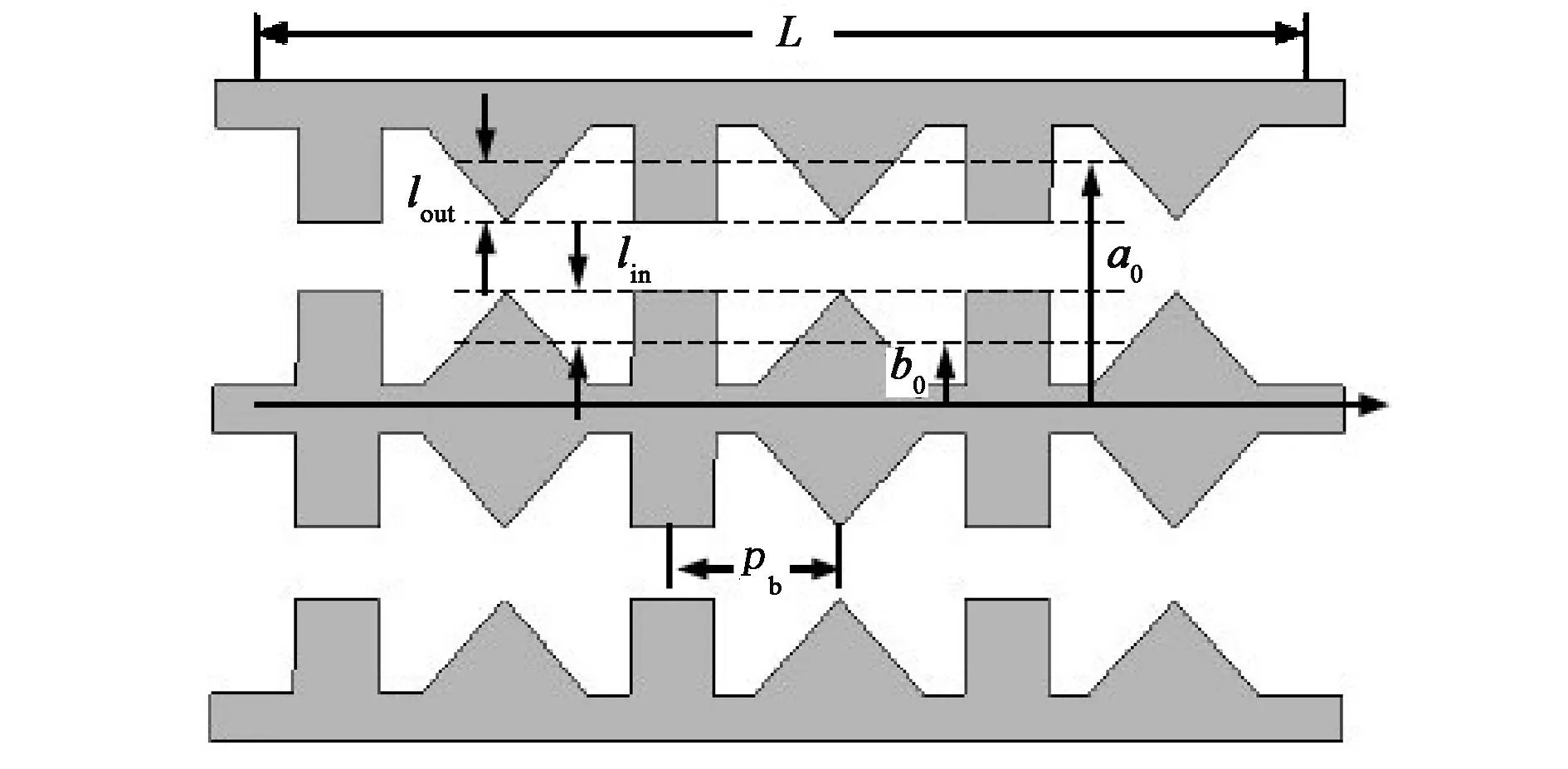
(a) 交替混合型开槽

(b) 分半混合型开槽
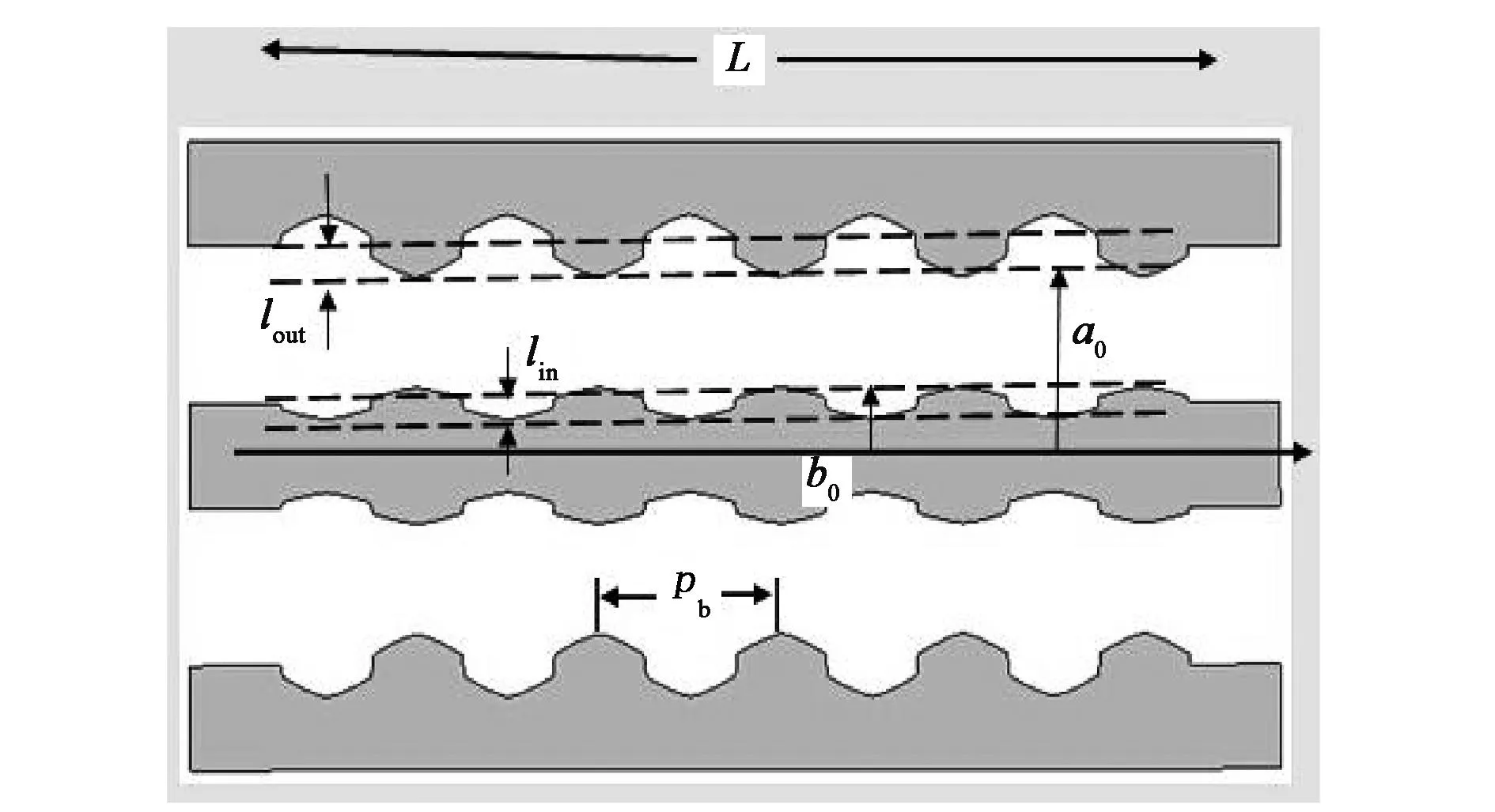
(c) 叠加混合型开槽图2 混合型同轴布喇格结构剖面图
根据吉布斯(Gibbs)现象[18-19],周期矩形波纹同轴布喇格结构f(z)傅里叶级数展开式为
(3)
则f(z)可以近似表示为
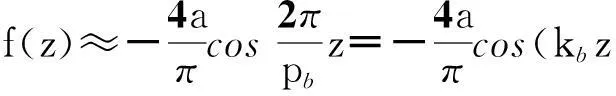
(4)
从而矩形波纹开槽同轴布喇格结构外壁半径Rout和内导体半径Rin可分别近似表示成关于纵向位置z变化的函数
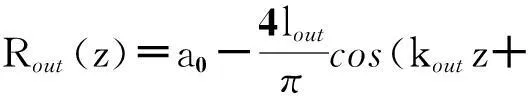
(5)
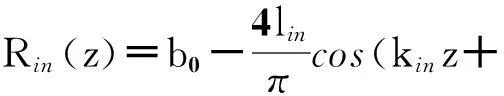
(6)
同样的方法,可得到周期三角形波纹开槽同轴布喇格结构外壁半径Rout和内导体半径Rin可分别近似表示成关于纵向位置z变化的函数:
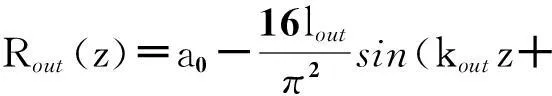
(7)

(8)
由方程(1)~(2)和(5)~(8)可知,三种不同开槽形状的同轴布喇格结构开槽槽深的关系为:
(9)
叠加混合型开槽同轴布喇格结构外壁半径Rout和内导体半径Rin可分别表示成关于纵向位置z变化的函数:
(10)
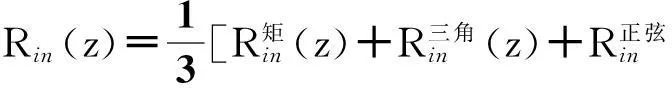
(11)
通过软件的数值计算,可求解出电磁场的具体分布,然后求解出每个模式的反射率,即布喇格结构入口处对应的反向波幅度与入口处工作模式正向波幅度比值的平方[20]:

(12)
本文利用自带程序编程求解麦克斯韦方程微波工作室MWS的CST软件平台[17]进行非线性数值模拟,该软件的可靠性已经在文献[8]中得到实验验证.利用CST软件平台时,为了得到更高的精度,在瞬态求解器控制对话框中设定精度参数为-50 dB,并使用完全自动的自适应网格加密;为了缩短仿真时间,假设结构材料为理想导体,并设置XY平面为磁对称面;经程序调试,设置软件的结构线度上最小网格点数(Lower mesh limit)为10,网格线比率限制(Mesh line ratio limit)设为12,则总的网格数达到3 346 560.
2单一开槽形状的比较研究
为了作更好的比较,采用文献[16]中英国斯特拉思克莱德大学(University of Strathclyde)曾进行同轴布喇格结构实验测试的一组典型参数,三种波纹开槽同轴布喇格结构的具体参数如表1所示.
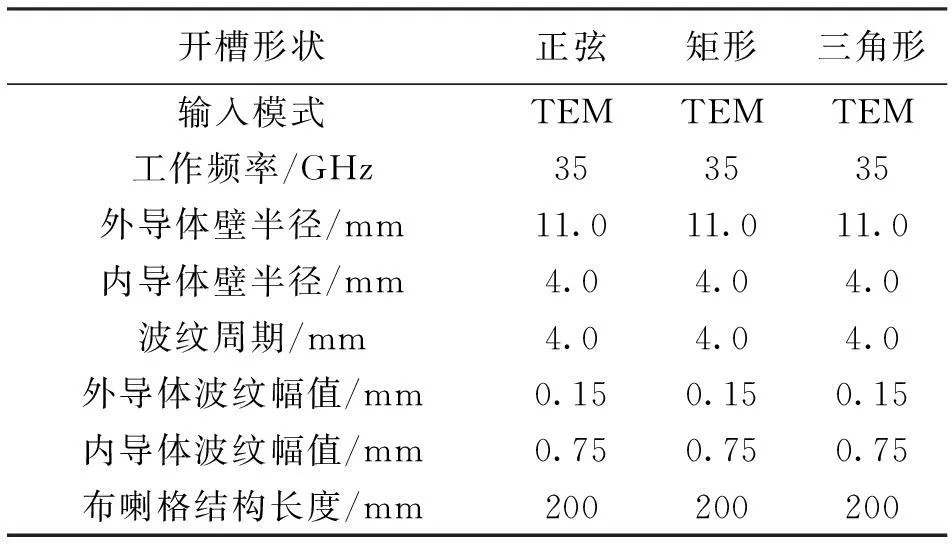
表1 三种波纹开槽同轴布喇格结构的参数
模拟仿真过程中,内外导体波纹槽的相对相位差δφ=|φin-φout|分别为0、π/2和π,并利用一个工作频率位于35~41.5GHz的TEM模式作为正向波的输入,实验结果发现结构中主要有工作模式TEM和耦合模式TM0,1两种模式:如果内外导体波纹槽的相对相位差δφ=|φin-φout|为π时,TEM模式发生前向波与反向波之间的自耦合(TEM↔TEM);当内外导体波纹槽的相对相位差δφ=|φin-φout|为0时,TEM与TM0,1模式发生相互耦合(TEM↔TM01);当内外导体波纹槽的相对相位δφ=|φin-φout|为π/2时,TEM模式除了在较低频率范围内发生自耦合外(TEM↔TEM)还和TM0,1在较高频率范围发生相互耦合(TEM↔TM01).
图3为当内外导体波纹槽相对相位差δφ=|φin-φout|分别为0,π/2和π时三种不同波纹开槽的同轴布喇格结构的反射率随频率的变化CST模拟关系曲线,图中矩形开槽频率响应曲线与文献[16]中报道的结果吻合一致.由图3可知,不管内外导体波纹槽的相对相位差δφ=|φin-φout|取0、π/2还是π,矩形开槽同轴布喇格结构频率响应的带宽最宽,三角形开槽同轴布喇格结构频率响应的带宽最窄,而正弦开槽同轴布喇格结构频率响应的带宽介于二者之间.

(a) 0
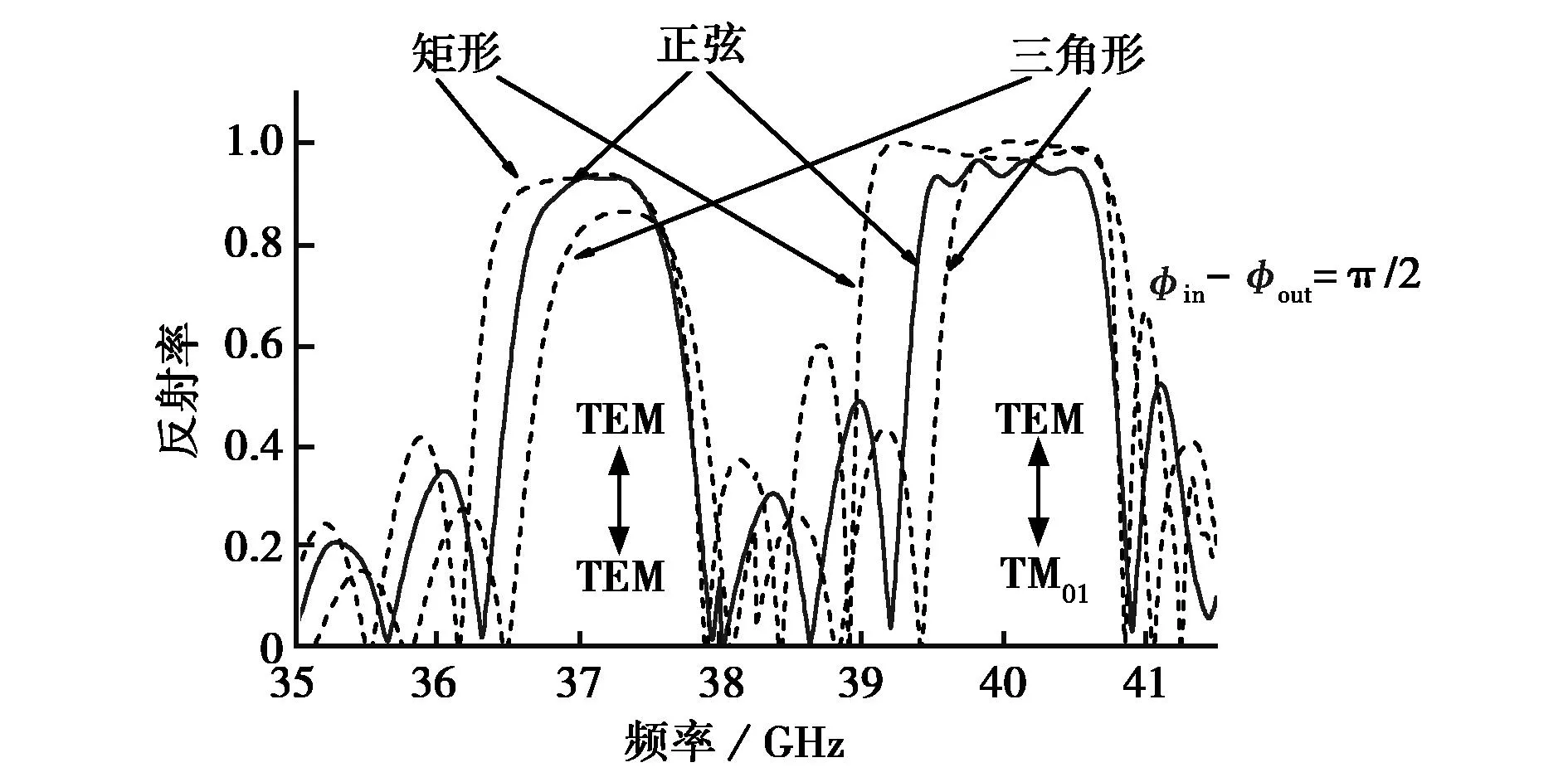
(b) π/2

(c) π图3 不同相位差时不同开槽形状同轴布喇格结构反射率随频率变化的模拟仿真图
3混合开槽形状对反射率的影响
基于三种单一开槽形状的同轴布喇格结构反射率随频率变化的频率响应比较结果,依然采用这一组典型参数来对混合型开槽同轴布喇格结构进行模拟比较研究,其参数如表2所示.
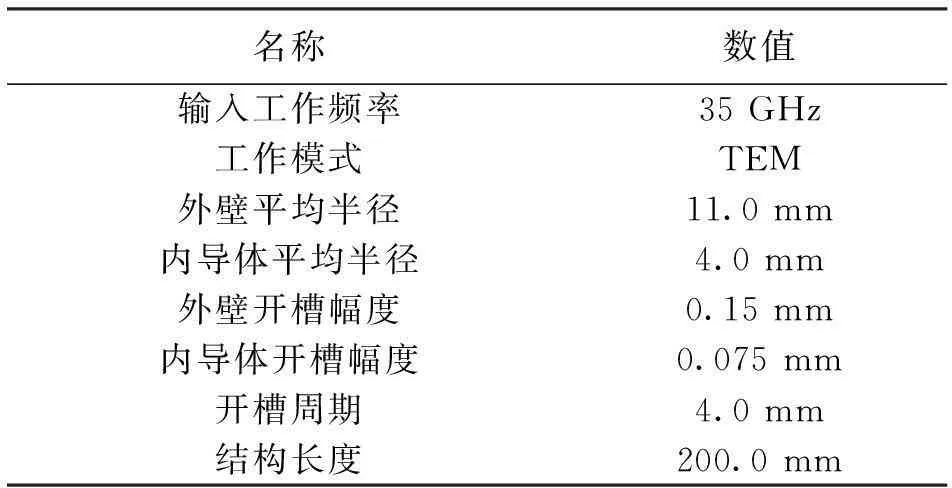
表2 同轴布喇格结构主要参数
图4和图5分别是内外导体波纹槽相对相位差δφ=|φin-φout|分别为0、π/2和π时交替混合型开槽和分半混合型开槽(实线)与单一开矩形和三角形槽(虚线)同轴布喇格结构反射率随频率变化关系的CST模拟仿真结果.从图4和图5中可看出,相对于单一开槽形状的同轴布喇格结构,交替混合型开槽同轴布喇格结构对耦合模式TM0,1的反射率有明显提高,高于单一开矩形和三角形槽结构,且反射率最大值几乎可达到 1,而分半混合型开槽同轴布喇格结构,不仅对耦合模式TM0,1的反射率有所提高,且其带宽也有明显变宽,无论是交替混合型开槽还是分半混合型开槽,其工作模式TEM的反射率和带宽都位于单一开矩形槽和三角形槽之间.
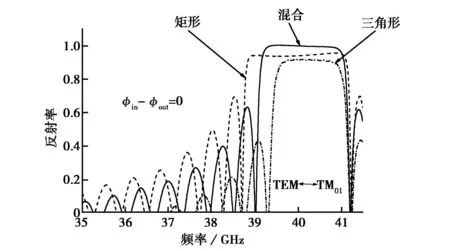
(a) 0

(b) π/2
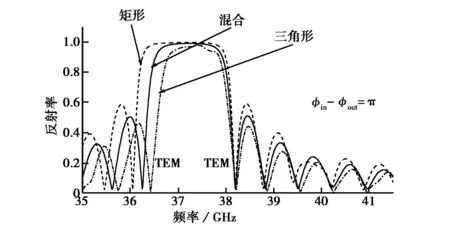
(c) π图4 不同相位差时交替混合型开槽同轴布喇格结构反射率随频率变化的模拟仿真图

(a) 0
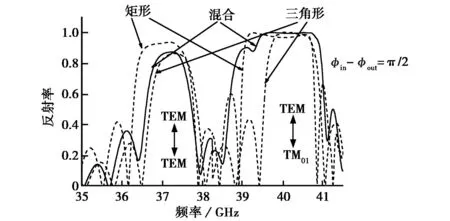
(b) π/2

(c) π图5 不同相位差时分半混合型开槽同轴布喇格结构反射率随频率变化的模拟仿真图
图6是内外导体波纹槽相位差分别为0、π/2和π的叠加型开槽(实线)与单一开矩形、三角形和正弦形槽(虚线)同轴布喇格结构反射率随频率变化关系的CST模拟仿真结果.不同于图4和图5的结果,当对同轴布喇格结构采取叠加混合型开槽时,不管是对于工作模式TEM还是对于耦合模式TM0,1,其反射率和带宽都位于单一开矩形槽和正弦形槽之间,反射率和带宽都略大于开正弦槽和三角形槽,残余旁瓣(residual side-lobes)的影响略小于开矩形槽[11-15],对模式的选择性能优于开矩形槽,仅其谐振频率点有所偏移.由图6(b)还可看出工作模式TEM和耦合模式TM0,1之间的带隙间隔,叠加混合型开槽大于开矩形槽,而小于三角形开槽,与正弦形开槽相近,所以,相比矩形开槽,叠加混合型开槽方式可以抑制带隙重叠现象[14].

(a) 0
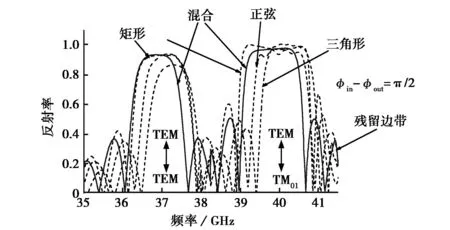
(b) π/2
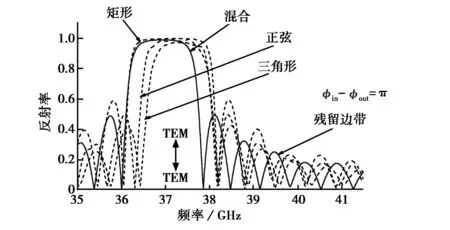
(c) π图6 不同相位差时叠加混合型开槽同轴布喇格结构反射率随频率变化的模拟仿真图
4结论
由于三角形、矩形以及交替混合和分半混合开槽都是不光滑的间断曲线,在间断点的突变容易导致高频电场击穿,而正弦和叠加混合开槽是光滑的连续曲线,不同的开槽形状对应于不同的边界条件,将导致有不同的模式耦合电磁特性[20].利用CST软件平台,对三种不同开槽形状和混合型开槽同轴布喇格结构进行了非线性数值模拟比较研究,从论文的CST软件模拟比较结果可以得出如下结论:
1) 在三种不同开槽形状同轴布喇格结构(矩形、三角形和正弦形)中,矩形开槽结构反射率随频率变化的频率响应的带宽最宽,而三角形开槽带宽最窄;
2) 交替混合型开槽同轴布喇格结构对耦合模式TM0,1的反射率有明显提高,反射率最大值几乎可达到1,而分半混合型开槽同轴布喇格结构,不仅其耦合模式TM0,1的反射率有所提高,且其频率带宽也明显加宽,无论是交替混合型开槽还是分半混合型开槽,其工作模式TEM的反射率和带宽都位于单一开矩形槽和三角形槽之间;叠加型开槽同轴布喇格结构,其结构形状克服了单一开矩形和三角形槽存在奇点和边界突变的缺点,无论是对于工作模式TEM还是对于耦合模式TM0,1,其反射率和带宽都位于单一开矩形槽和正弦形槽之间,反射率和带宽略大于开正弦槽,残余旁瓣的影响小于开矩形槽,对模式的选择性能优于开矩形槽,且其谐振频率点有所降低,因此,叠加混合型开槽是较好的选择.
在实际科技工程应用中,可以根据需要选择布喇格结构的形状和尺寸以及开槽方式,保证腔体大尺寸工作,便于散热,降低模式竞争,以提高同轴布喇格结构的反射效率和模式选择性能,进而提高器件的输出功率和效率增益.
参考文献
[1] BARROSO J J, LEITE N J P. Design of coaxial Bragg reflectors [J]. IEEE Trans on Plasma Sci, 2006, 34: 666-672.
[2]赖颖昕,杨雷, 张世昌. 矩形槽同轴布拉格结构的模式匹配分析方法及实验验证[J]. 物理学报, 2013, 62(20): 208402.
LAI Yingxin, YANG Lei, ZHANG Shichang. Mode-matching analytic method of a coaxial Bragg structure corrugated with rectangular ripples and its experimental verification[J]. Acta Phys sin, 2013,62(20):208402.(in Chinese)
[3] JI Y P, WANG S J, XU J Y, et al. Effect of normalized plasma frequency on electron phase-space orbits in a free-electron laser[J]. Chin Phys B, 2014, 23(2):024103.
[4] DATTOLI G, DI PALMA E, DORIA A, et al. The Gyratron, CARM and FEL devices: an analytical unified formulation for the small signal analysis [C]//2014 Tenth Internationa Vacuum Electron Sources Conference (IVESC), st. Petersburg, June 30-July 4, 2014: 14565842.
[5] LAI Y X, ZHANG S C, ZHANG H B. A coaxial bragg reflector for cyclotron autoresonance maser oscillator [J].IEEE Microwave and Wireless Components Letters, 2007, 17:328-330.
[6] HUANG Jie, WEI Tao, FAN Jun, et al. Coaxial cable Bragg grating assisted microwave coupler [J]. Review of Scientific Instruments, 2014,85(1):014703.
[7] 邓峰,赵正予,张援农.高频电波加热电离层对波传播影响的研究[J].电波科学学报,2007,22(6):976-981.
DENG Feng, ZHAO Zhengyu, ZHANG Yuannong. Influence of HF heating on transmission of electromagnetic wave[J]. Chinese Journal of Radio Science, 2007,22(6):976-981.(in Chinese)
[8] ZHANG S C, CHEN X H, LAI Y X. Effect of eccentricity on transmission in a coaxial Bragg structure [J]. Int J Infrared Millimeter Waves, 2007, 28(12):1043-1050.
[9] DING X Y, ZHANG S C. Effect of ripple shape and taper on frequency response of reflectivity and transmission in a coaxial Bragg structure[J].J Appl Phys, 2009, 42: 085104.
[10]赖颖昕,谭永明. 60GHz 缺陷态同轴布喇格波导窄带带通滤波器设计及性能分析[J]. 电子与信息学报,2012,34 (8):2023-2027.
LAI Yingxin, TAN Yongming. Design and Analysis of a 60 GHz narrowband band-pass filter based on defected coaxial bragg waveguide [J]. Journal of Electronics &Information Technology, 2012, 34(8):2023-2027.(in Chinese)
[11]丁学用,张世昌,谢永超. 具有坡度的同轴布喇格结构的频率响应[J]. 强激光与粒子束, 2008,20(12):2051-2054.
DING Xueyong, ZHANG Shichang, XIE Yongchao. Characteristics of frequency response in a coaxial Bragg structure with tapered ripples[J]. High Power Laser and Particle Beams, 2008, 20(12):2051-2054.(in Chinese)
[12]LAN Feng, YANG Ziqiang, QI Limei, et al. Compact waveguide bandpass filter employing two-dimensional metallic photonic crystals for millimeter to terahertz frequencies [J]. Chinese Optics Letters, 2014, 12(4): 040401.
[13]DING X Y, LIU H, LÜ Z S. Effect of ripple taper on coupling modes in a coaxial Bragg structure[J]. Int J Infrared Millimeter Waves, 2010, 31(10):1156-1163.
[14]DING X Y, LI H F, LÜ Z S. Effect of ripple taper on band-gap overlap in a coaxial bragg structure operating at terahertz frequency [J]. Phys Plasmas, 2012, 19: 092105.
[15]丁学用,王玲玲. 新型坡度同轴布喇格反射器数值模拟比较研究[J]电波科学学报, 2011, 26(1):55-61.
DING Xueyong, WANG Lingling. Comparative Study of Numerical Simulations of characters of frequency response in coaxial Bragg reflector with the new tapered ripples[J].Chinese Journal of Radio Science, 2011,26(1):55-61.(in Chinese)
[16]KONOPLEV I V, MCGRANE P, PELPHS A D R, et al. Observation of photonic band-gap control in one dimensional Bragg structures[J]. Appl Phys Lett,2005, 87:121104.
[17]CST-Microwave Studio. Computer Simulation Technology (CST), User’s Manual 5[M]. 2003.
[18]吴大正,杨林耀,张永瑞.信号与线性系统分析[M].4版. 北京:高等教育出版社,2010.
[19]李克勤,姜翠香.吉布斯现象的MATLAB实现[J].三峡大学学报:自然科学版,2006,28(3):269-270.
LI Keqin, JIANG Cuixiang. Realization of Gibbs Phenomenon based on matlab [J]. Journal of China Three Gorges Univ:Natural Sciences, 2006, 28(3):269-270.(in Chinese)
[20]LAI Y X, ZHANG S C. Multiwave interaction formulation of a coaxial Bragg structure and its experimental verification [J].Phys Plasmas, 2007, 14:113301.

丁学用(1979-),男,河南人,讲师,硕士, 研究方向:高功率微波、海洋通信等.

王玲玲(1985-),女,河南人,讲师,硕士,研究方向:自动控制、通信中的信号处理等.
吕振肃(1946-),男,山西人,教授,硕士,研究方向:信号处理等算法.
刘恒, 刘波, 谢广钱, 等. 迭代傅里叶算法用于六边形稀疏阵列天线[J]. 电波科学学报,2015,30(6):1235-1240. doi: 10.13443/j.cjors. 2015012102
LIU Heng, LIU Bo, XIE Guangqian, et al. Iterative Fourier technique applied for Hexagon thinned array [J]. Chinese Journal of Radio Science,2015,30(6):1235-1240. (in Chinese). doi: 10.13443/j.cjors. 2015012102
Comparative study of coaxial Bragg structure with
hybrid ripples shape
DING XueyongWANG LinglingLÜ Zhensu
(ThePolytechnicInstituteofSanYaUniversity,Sanya572022,China)
AbstractBased on the Computer Simulation Technology (CST) software, numerical simulations are carried out for comparative study about the frequency response characteristic of the coaxial Bragg structure with different ripples shapes. Results show that the triangular ripples has the narrowest bandwidth, while the bandwidth of rectangular ripples is the widest. Moreover, the reflectivit of coupling mode is obviously improved with the alternate hybrid ripples, and for the half-and-half ripples, the reflectivity of coupling mode is improved and its bandwidth is widened. Besides, whether coaxial Bragg structure employs the alternate hybrid ripples or the half-and-half ripples, the reflectivity and the bandwidth of the working mode are both between the sole rectangular ripples and triangular ripples. However, the overlie ripples overcomes the defects that the sole rectangular ripples and triangular ripples have singularity and sudden border changes, and its mode selectivity is better than rectangular ripples, furthermore its reflectivity and bandwidth are better and wider than that of the sole sinusoidal and trian-gular ripples, excepting the minus deviation of its syntony frequency point. These features are propitious to the mode selectivity, heat dissipation and the machining manufacture of the coaxial Bragg structure.
Key wordscoaxial Bragg structure; alternate ripples; half-and-half ripples; overlie ripples; reflectivity
作者简介
项目基金资助项目: 海南省自然科学基金(614252); 海南省教育厅教改(Hnjg2015-61); 三亚市重点实验室基金(L1305)资助课题
收稿日期:2015-01-15
中图分类号TN129
文献标志码A
文章编号1005-0388(2015)06-1228-07
