矩形金属机壳孔缝电磁耦合特性研究

吴刚　孙靖虎　李兵　张晓阳

(中国空间技术研究院西安分院,西安 710100)



矩形金属机壳孔缝电磁耦合特性研究

吴刚孙靖虎李兵张晓阳

(中国空间技术研究院西安分院,西安 710100)

摘要针对矩形金属机壳上孔缝在高功率电磁环境下的电磁耦合问题,提出了一种使用模式匹配法和基于矩量法求解的混合位积分方程来分析孔缝电磁耦合特性的全波混合算法.该算法考虑了高次模、孔缝形状、孔缝厚度以及入射波极化方向等因素对电磁耦合特性的影响.通过将数值仿真结果与经典孔缝电磁耦合模型的测试结果进行对比,验证了该算法具有较高的准确性,与经典的时域有限差分法相比,该算法具有很高的计算效率.研究结果表明:有孔金属机壳在外界强电磁辐射条件下具有明显的谐振效应,在谐振频率点,耦合进入机壳的电场将大大增强,且孔缝附近以及机壳中心的耦合电场峰值要高于其他位置的耦合电场峰值;随着机壳表面上孔缝厚度的增加,耦合进入其内部的电场也在减弱;当机壳上的孔缝为矩形且入射波的电场极化方向平行于矩形缝隙的短边时,对应于该极化方向的孔缝电场耦合强度是所有极化方向中最强的.

关键词高功率微波;电磁耦合;数值计算;金属机壳;矩形孔缝

引言

根据国际电工委员会的标准,将入射电场超过100 V/m的环境称为高功率电磁环境[1],如何提高电子系统在高功率电磁环境下的生存能力问题在近些年来越来越突出,一般来说,电子设备的金属机壳通常被用来对外界强电磁干扰进行屏蔽,但与此同时金属机壳上不可避免的孔缝也大大降低了其对外界强电磁场的屏蔽能力.为了限制外界电磁干扰能量通过孔缝耦合进入到金属机壳的量级,进而避免内部敏感电子元器件受到外界强电磁场干扰的损伤,就十分有必要对有孔金属机壳的电磁耦合特性进行分析.目前金属机壳孔缝电磁耦合特性的分析方法主要分为数值方法和等效传输线法.数值方法主要包括时域有限差分法(Finite Difference Time Domain,FDTD)[2-3]、矩量法(Method of Moments,MoM)[4]、有限元法(Finite Element Method,FEM)[5]以及混合算法[6-7],其应用范围较广,但计算耗时耗资源;等效传输线理论[8-9]虽然计算速度快,但由于做了很多近似处理,应用范围有限.

基于此提出一种全波混合算法,应用模式匹配法和基于矩量法的混合位积分方程分析计算矩形金属屏蔽机壳的孔缝电磁耦合特性,该算法不仅具有较高的计算效率,而且考虑到了孔缝厚度、孔缝形状、入射波极化方向以及高次模等因素对电磁耦合特性的影响,因此也更适用于普遍情况.

1理论分析

如图1所示的矩形金属机壳,其尺寸为a×b×h,侧壁的厚度为t,在其一侧壁上开一个尺寸为w×l的矩形孔缝,外界电磁波垂直于孔缝所在壁面照射该金属机壳.根据Schelkunoff场等效原理,将孔缝所在平面z=t可近似等效为无限大的导电平面,因此该电磁耦合问题可划分为内部问题和外部问题两部分.所谓内部问题包括金属机壳内的矩形区域Ⅰ(-ht),等效模型如图2所示.

图1　有孔矩形机壳示意图

图2　等效模型示意图

1.1　内部问题

由于区域I和区域Ⅱ可被认为是两个矩形波导,因此电磁波在这两个矩形波导之间各传播模式的幅度系数可用模式匹配法求解.从Maxwell方程出发,引入电、磁矢量位函数Ae和Ah,由其z向分量Aez和Ahz可以得到Ⅰ、Ⅱ波导内的横向电磁场表达式:

(1)

(2)

(3)

(4)

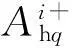
由此,在Ⅰ、Ⅱ区中沿+z与-z方向传播模式的幅度系数矩阵Ai+和Ai-可分别表示为

(5)

根据Ⅰ、Ⅱ区交界面处电场与磁场切向分量连续,可推得Ⅰ、Ⅱ区中TE模式和TM模式的耦合系数,从而可得耦合系数矩阵M[11].

通过模式匹配法,得到Ⅰ区与Ⅱ区中模式幅度系数矩阵的耦合对应关系表达式为

(1)治疗前,两组患者的三项心功能指标(左心室射血分数、左心室舒张末期内径、左心房舒张末期内径)比较差异不显著,P>0.05,无统计学意义;(2)治疗后,两组患者的三项心功能指标(左心室射血分数、左心室舒张末期内径、左心房舒张末期内径)比较差异显著,P<0.05,有统计学意义,详见表1.

AI++AΙ-=M(AⅡ++AⅡ-) ;

(6)

MT(AI+-AI-)=AⅡ+-AⅡ-.

(7)

由于区域Ⅰ可看作是终端短路的矩形波导,因此在z=—h处可以得到

AI+=-LIAI-.

(8)

AⅡ+=ρAⅡ-.

(9)

式中: ρ=(U+P)-1(U-P); P=MT(LI+U)(U-LI)-1M,U是一个2N×2N的单位矩阵.将式(8)和式(9)代入式(6)与式(7)中,得到矩阵方程

AI-=(U-LI)-1M(ρ+U)AⅡ-.

(10)

1.2　外部问题

如图2所示,在Ⅰ区将外界通过z=t无限大导电平面上孔缝的激励场等效为面磁流Ms

(11)

式中, n为外法向矢量.根据镜像原理,Ⅲ区由等效磁流2Ms所感生的磁场为[12]

HMs=-jωF(r)-φm(r) .

(12)

式(12)中,在场点处的电矢位函数F和磁标位函数φm可表示为:

(13)

(14)

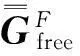
1.3　矩阵运算

根据电磁场在不连续面两侧切向分量相等的原理,在区域Ⅲ与区域Ⅱ相交的孔缝表面处建立方程

(15)

等效面磁流Ms可用正交基函数展开:

(16)

由矩量法Galerkin法则,构建2N×1的权函数矩阵W为

(17)

在式(15)两边同乘该权函数,并在Sa面上积分,根据展开函数的正交性,可得矩阵方程

TK+Iinc=Z.

(18)

式中:

TK=-jω〈W, F〉+〈tW,φm〉,

K=LIIAII++(LII)-1AII-;

如果外界电磁环境已知,联合式(9)和式(18),就可以得到未知量模式幅度系数AII-为

AII-=[(LIIρ-(LII)-1)-T(LIIρ+

(LII)-1)]-1·Iinc.

(19)

将式(19)带入矩阵方程(8)和(10)中,所有在Ⅰ区中传播模式的幅度系数都可以计算得到,由此,该模型中屏蔽体内任一点的电场强度可由式(1)计算出.

2实验结果分析

为了研究强电磁环境下有孔金属机壳内的电场分布特性,以一个典型的金属机箱外壳为研究对象,其尺寸为30cm×12cm×30cm,一个10cm×0.5cm的孔缝开在该机箱一个侧面上的中心位置处,机箱壁采用理想导体材料,其厚度为t=1.5mm,机箱内外的空气都当作理想状态来考虑.

2.1　算法验证

外界电磁波正对孔缝所在壁面垂直入射,其电场极化方向平行于矩形缝隙的短边,电场强度为377V/m,测试点在该屏蔽体中心的位置处,且有50个TE模和50个TM模.

从图3可以看到,仿真结果与文献[13]中的测试结果吻合良好,有孔金属机壳在外界电磁波的照射下具有谐振特性,即在700MHz的谐振点附近,耦合进入该机壳的电磁能量大大提高了.用一台商务计算机在20个频点计算上述模型的耦合电场大概需要12min,所需内存大约200MByte,而同样的算例用FDTD算法编程仿真20个频点所需时间约55min[14],所耗内存大约350MByte,由此可见该混合算法不仅具有很高的准确性,而且还有较高的计算效率.

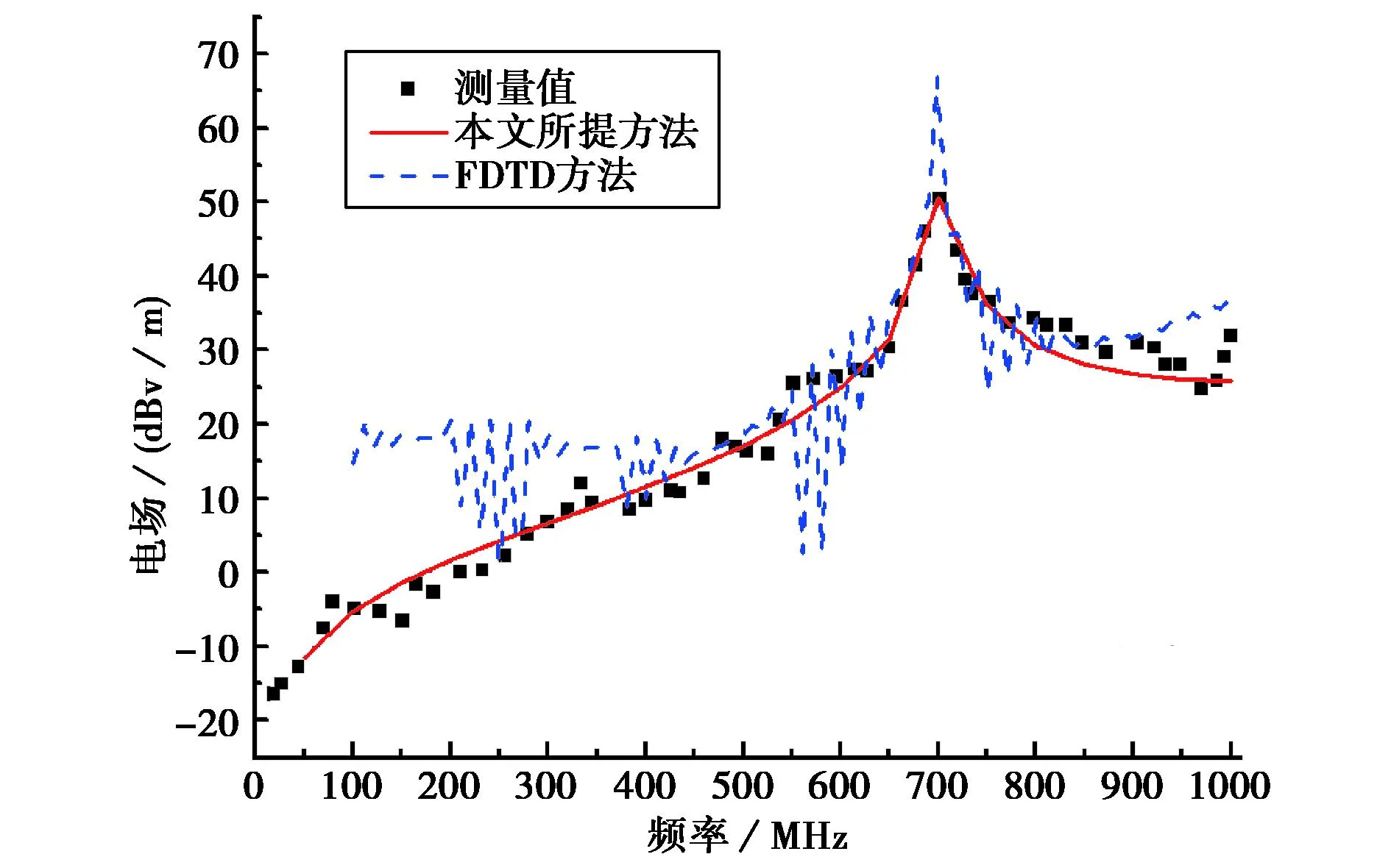
图3　矩形机壳中心处耦合电场强度仿真与测试结果对比图

2.2　机壳内的电场分布

由于有孔金属机壳在外界微波辐射下有明显的谐振特性,因此在谐振频率点机壳内的电场分布是我们十分感兴趣的.以上述有孔金属机壳为例,在700MHz的谐振频率点上,机壳内孔缝附近和中心处xoy平面上的电场分布如图4和图5所示.从图4可以看到缝隙附近的耦合电场峰值比入射微波脉冲的电场峰值大,即在孔缝附近会出现耦合场强增强的现象,尤其是在孔缝中心位置处,电场强度较高,这主要是由于孔缝与金属机壳内的电磁场相互作用以及高次模的影响所造成.图5展示了在700MHz的谐振频率点上,机壳中心位置处xoy截面上的电场分布图,可以看出,耦合电场的强度沿y轴并无明显的变化,而耦合电场的强度在机壳x轴的中心处最强,且从中心位置向x轴两侧逐渐减弱.

图4　机壳内孔缝处(z=0 cm)xoy面电场分布图 (700 MHz)

图5　机壳中心处xoy面(z=-15 cm)电场分布图 (700 MHz)

图6和图7分别描述了金属机壳中心yoz和xoy平面在700 MHz谐振频率点的电场分布.可以看到机壳内孔缝附近处的耦合电场强度较高,进一步验证了孔缝处场强会增强的结论,此外随着耦合能量沿-z方向的传播,高次模迅速衰减,但由于机壳的谐振特性,在机壳中心处,耦合电场也较强,这主要由机壳本征频率的主模式构成.因此在布局时,应尽量避免将敏感器件放置在机壳孔缝附近及机壳中心处,此外,还应避免电子线路的本征频率与机壳的谐振频率重合,减轻谐振特性对电路造成的破坏.

图6　机壳中心处yoz面(x=15 cm)电场分布图

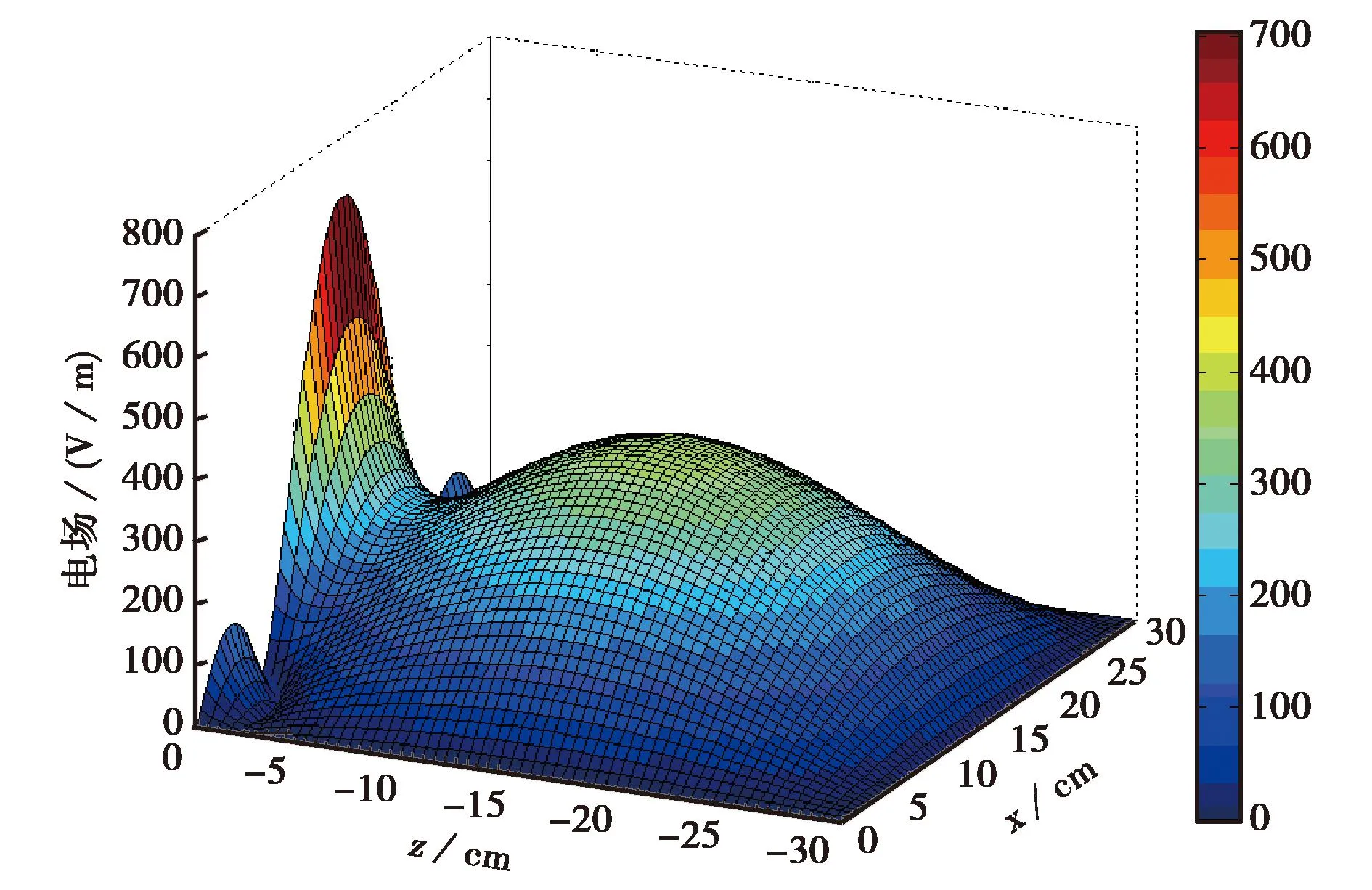
图7　机壳中心处xoz面(y=6 cm)电场分布图

2.3　孔缝厚度的影响

为了研究孔缝的厚度对电场耦合的影响,在尺寸为30 cm×12 cm×30 cm的金属机壳上,选取一组孔缝厚度参数t进行分析,孔缝的厚度分别为:0.5、1.5、3.0、5.0、8.0、10.0 mm,在入射波垂直入射且极化方向为垂直极化时,机壳内中心处的电场强度如图8所示.

图8　具有不同孔缝厚度的矩形机壳中心位置耦合电场

从仿真结果可以发现,随着机壳面上孔缝厚度参数t的增加,机壳内耦合电场的强度也在逐步减弱.因此在实际工程中,为了提高分机金属机壳对外界电磁波的屏蔽能力,应在机壳孔缝处进行局部加厚处理,或者在接缝处采用非直通缝搭接的方法,增加孔缝的等效厚度,达到减少外界电磁波直接耦合的目的,从而保护机壳内部的电路及其敏感元器件.

2.4　电场极化方向的影响

为了研究入射波极化方向对机壳上孔缝电磁耦合特性的影响,本章还是选取上述内壁尺寸为30cm×12cm×30cm的金属机壳,其侧壁上的孔缝尺寸为10cm×0.5cm,入射波垂直照射分机机壳上孔缝所在的侧壁.在两种极端情况下,即入射波的极化方向分别为垂直极化(入射平面波的电场方向垂直于矩形孔缝的长边)和平行极化(入射平面波的电场方向平行于矩形孔缝的长边),入射波极化方向对矩形机壳孔缝电场耦合的影响如图9所示.从仿真结果可以很明显的看到,当入射波的电场极化方向为垂直极化时,金属机壳的孔缝电场耦合要高于平行极化时的孔缝电场耦合.因此可以得出一个结论:当屏蔽机壳上的孔缝为矩形且入射波的电场极化方向平行于矩形缝隙的短边时,对应于该极化方向的机壳孔缝电场耦合是所有极化方向中最差的.相反,当入射波的电场极化方向垂直于矩形缝隙的短边时,对应于该极化方向的机壳孔缝电场耦合是所有极化方向中最好的.

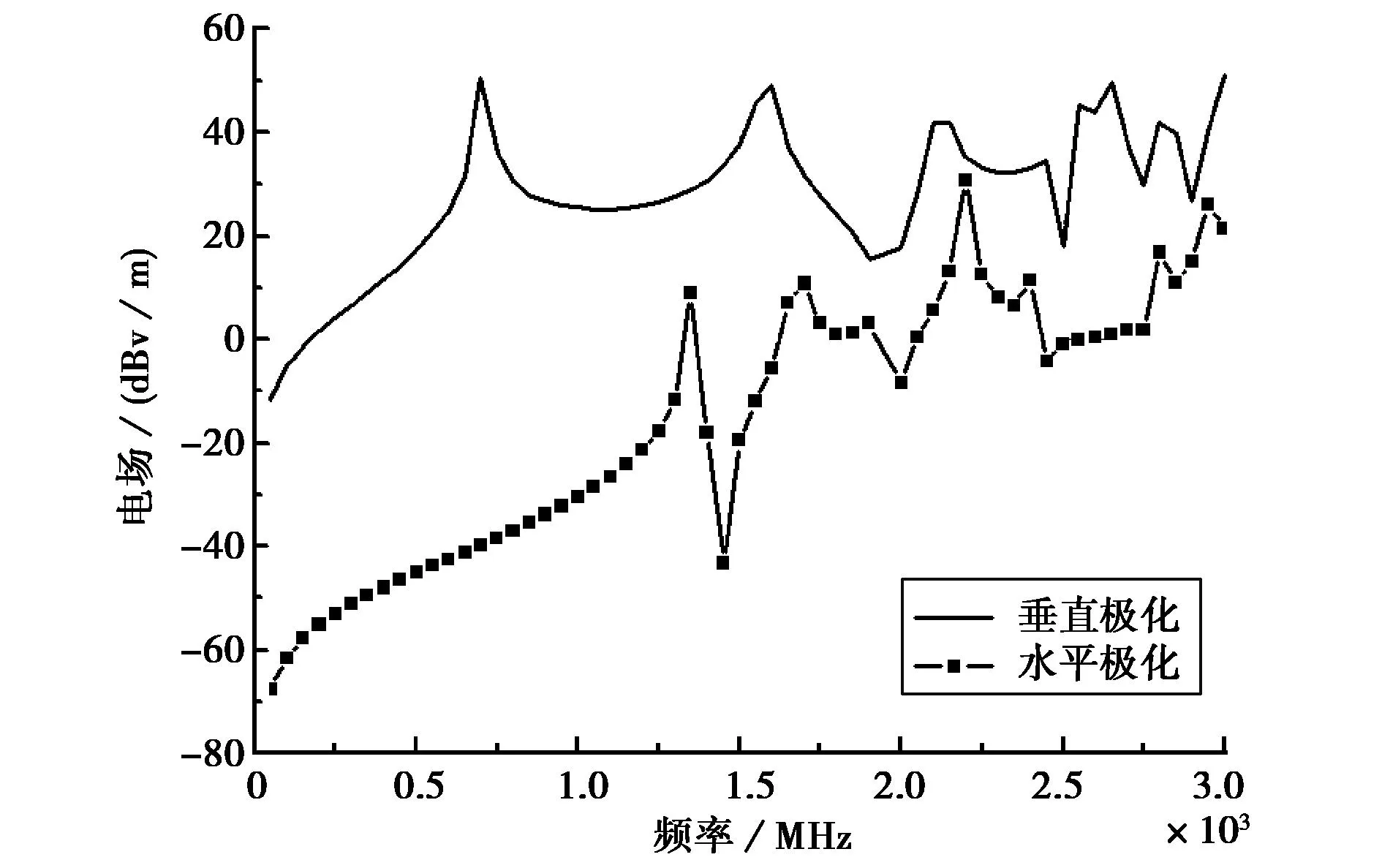
图9　不同极化方向时的带孔缝矩形机壳中心处的耦合电场

3结论

应用模式匹配法以及基于矩量法求解的混合位积分方程,对在强电磁环境下有孔金属机壳的电磁耦合特性进行了研究,不难发现有孔金属机壳在外界高功率微波辐射下有明显的谐振特性,在谐振频点上,耦合进入到金属机壳内部的电场强度高于其他频点,对机壳内部电路及敏感半导体器件的损伤概率较高,且通过对不同孔缝厚度以及入射波极化特性对有孔机壳电磁耦合特性的数值分析,得出了一些规律性的结论.该研究为对机壳内部的敏感半导体器件进行合理布局,以提高电子设备在高功率电磁环境下的生存能力提供了设计依据,而且对于如何设计金属屏蔽体以最大限度的减小电磁耦合带来的损失也具有重要的参考价值.

参考文献

[1]IECStandard.ElectromagneticCompatibility(EMC)-Part2-13:Environment-high-powerElectromagnetic(HPEM)Environments-RadiatedandConducted[S]. 61000-2-13, 2005.

[2]CHENJ,ZHANGA.AsubgriddingschemebasedontheFDTDmethodandHIE-FDTDmethod[J].ACESJournal, 2011, 26(1): 1-7.

[3]LEIJZ,LIANGCH,ZHANGY.StudyonshieldingeffectivenessofmetalliccavitieswithaperturesbycombiningparallelFDTDmethodwithwindowingtechnique[J].ProgressinElectromagneticsResearch, 2007, 74: 85-112.

[4]ARANEOR,LOVATG.FastMoManalysisoftheshieldingeffectivenessofrectangularenclosureswithapertures,metalplates,andconductingobjects[J].IEEETransElectromagnCompat, 2009, 51(2): 274-283.

[5]BENHASSINES,PICHONL,TABBARAW.Anefficientfinite-elementtime-domainmethodfortheanalysisofthecouplingbetweenwaveandshieldedenclosure[J].IEEETransMagn, 2002, 38(2): 709-712.

[6]YENIKAYAS,AKMANA.HybridMoM/FEMmodelingofloadedenclosurewithapertureinEMCproblems[J].IntJRFandMicrowaveCAE, 2009, 19: 204-210.

[7]郝翠, 李邓化.关于双层带孔缝腔体的屏蔽效能研究[J].电波科学学报, 2014, 29(1): 114-121.

HAOCui,LIDenghua.Shieldingeffectivenessofdouble-deckcavitywithapertures[J].ChineseJournalofRadioScience, 2014, 29 (1):114-121. (inChinese)

[8]张旭锋, 李颖, 倪谷炎, 等.有孔腔体屏蔽效应分析的混合模型[J]. 电波科学学报, 2011, 26(1): 25-29.

ZHANGXufeng,LIYing,NIGuyan,tea1.Hybridmodeltoevaluatingshieldingeffectivenessofcavitywithapertures[J].ChineseJournalofRadioScience, 2011,26(1): 25-29.(inChinese)

[9]张亚普, 达新宇, 谢铁城. 偏心孔缝箱体屏蔽效能电磁拓扑分析算法[J]. 电波科学学报, 2014, 29(5): 994-1002.

ZHANGYapu,DAXinyu,XIETiecheng.Electromagnetictopologyalgorithmofshieldingeffectivenessanalysisofametallicenclosurewithoff-centreapertures[J].ChineseJournalofRadioScience, 2014, 29(5): 994-1002.(inChinese)

[10]张本全.微波无源器件设计中的模式匹配法研究[D].成都: 电子科技大学, 2004.

ZHANGBenquan.ResearchonMode-matchingMethodinMicrowavePassiveComponentDesign[D].Chengdu:UniversityofElectronicScienceandTechnologyofChina, 2004.(inChinese)

[11]WUG,ZHANGXG,LIUB.Ahybridmethodforpredictingtheshieldingeffectivenessofrectangularmetallicenclosureswiththicknessapertures[J].JournalofElectromagnWavesandAppl, 2010, 24(8/9): 1157-1169.

[12]HARRINGTONRF.Time-HarmonicElectromagneticFields[M]. 2nded.IEEEPress, 2001.

[13]ROBINSONMP,BENSONTM,CHRISTOPOULOSC,etal.Analyticalformulationfortheshieldingeffectivenessofenclosureswithapertures[J].IEEETransElectromagnCompat, 1998, 40(3): 240-247.

[14]CELOZZIS,ARANEOR,LOVATG.ElectromagneticShielding[M].NewJersey:JohnWiley&Sons, 2008.

吴刚(1981-),男,陕西人,博士,主要从事高功率微波防护技术研究．

孙靖虎(1983-),男,湖北人,硕士,主要从事微波有源技术研究．

李兵(1982-),男,陕西人,博士,主要从事无线通信系统技术研究．

张晓阳(1985-),男,陕西人,博士研究生,主要从事电磁仿真技术研究．

丁学用,王玲玲,吕振肃.混合型开槽同轴布喇格结构的比较研究[J].电波科学学报,2015,30(6):1228-1234.doi:10.13443/j.cjors. 2015011501

DING Xueyong, WANG Lingling, LÜ Zhensu. Comparative study of coaxial Bragg structure with hybrid ripples shape[J]. Chinese Journal of Radio Science,2015,30(6):1228-1234. (in Chinese). doi:10.13443/j.cjors. 2015011501

Prediction for the electromagnetic coupling characteristics

of a metallic enclosure with apertures

WU GangSUN JinghuLI BingZHANG Xiaoyang

(Xi’andivisionofChinaAcademyofSpaceTechnology,Xi’an710100,China)

AbstractAiming at prediction for the electromagnetic coupling characteristics of a metallic enclosure with a rectangular aperture, this paper proposes a hybrid approach which applies the mode-matching technique and the mixed potential integral equation based on the method of moments. The effects of high-order modes, aperture shape, aperture thickness, and polarization direction of incident wave are all considered in the simulation. The simulation results are compared with data obtained by measurement and finite-difference time-domain method to validate the accuracy and the efficiency of the proposed approach. The research shows that there is an obvious resonance when electromagnetic waves penetrating the metallic enclosure with a rectangular aperture; the coupling electric fields around the aperture and center of the enclosure are enhanced at the resonant frequency; with the thickness of the apertures growing, the coupling electric fields weaken; when the polarized direction of the incident wave is parallel to the short side of the rectangular aperture, the coupled electric fields attain the maximum.

Key wordshigh power microwave; electromagnetic coupling; numerical calculation; metallic enclosure; rectangular aperture

作者简介

收稿日期：2015-01-12

中图分类号TN81

文献标志码A

文章编号1005-0388(2015)06-1222-06