卫星桁架结构跨尺度热—力耦合优化设计与分析

马健 张宏宇 闫亮 冉治国

(1 北京空间飞行器总体设计部，北京 100094) (2 北京机械设备研究所，北京 100854)



卫星桁架结构跨尺度热—力耦合优化设计与分析

马健1张宏宇1闫亮1冉治国2

(1 北京空间飞行器总体设计部，北京 100094) (2 北京机械设备研究所，北京 100854)

卫星飞行过程中，高精度测量设备的复合材料支撑结构经历多种温度环境，影响结构的热稳定性。为对其热学性能进行研究，综合考虑热—力耦合优化设计，首先，发展了复合材料热膨胀系数跨尺度数值模型。在微观模型中，通过建立代表性体积单元(Representative Volume Element,RVE)模型，由纤维热膨胀系数计算得到单向复合材料热膨胀系数；建立复合材料构件宏观模型，采用微观模型计算得到的热膨胀系数对宏观模型进行分析与计算。为验证复合材料热膨胀系数跨尺度数值模型的正确性，对复合材料管件的热膨胀性能进行了试验测试，测试结果与数值计算结果具有很好的一致性。其次，对卫星桁架杆件进行热稳定性优化设计与分析，综合考虑管件的热膨胀系数与刚度的约束条件，采用具有二阶收敛特性的共轭梯度法对复合材料构件的铺层进行优化设计，发展了复合材料桁架结构热—力耦合优化设计流程。最后，针对某卫星天线桁架支撑结构进行了定热膨胀系数设计与分析，结果表明采用跨尺度热—力耦合优化设计方法得到的热变形量远小于天线支撑结构给定的指标。该方法可用于卫星复合材料桁架结构热稳定性设计与分析。

桁架结构；跨尺度；优化设计；热稳定性；代表性体积单元；热膨胀系数；卫星

1 引言

卫星飞行过程中，平台及支撑结构将经历多种温度环境，影响结构的热稳定性；为满足卫星高精度测量设备及高分辨率有效载荷的设计安装要求，对平台及支撑结构的热稳定性提出了更高的要求[1-3]。复合材料由不同的组分组成，各组分对复合材料结构热稳定性的影响至关重要。采用试验的方法对材料的热性能进行分析成本较大，通过数值模拟对材料的热性能进行分析是工程上可行的方法。通过建立复合材料热性能分析的跨尺度计算模型，由复合材料微观尺度的热膨胀系数得到结构宏观尺度的热性能，对研究复合材料结构的热分析具有非常重要的意义。文献[4-5]通过有限元方法，系统地研究了单向复合材料的线性热膨胀系数，为数值方法在复合材料热膨胀性能的应用提供了新的思路，但分析对象仍局限于线性热膨胀系数。文献[6]采用三维微观力学建模方法，对宏观各向同性的金属-陶瓷复合材料的热膨胀性能进行了研究，三维模型可以得到更精确的复合材料的热膨胀性能，但该文献只给出了各向同性材料的数值分析方法。文献[7]建立了三维编织复合材料的代表性体积单元(Representative Volume Element,RVE)模型对复合材料热膨胀系数进行预测，进一步提高了热膨胀系数的计算精度。文献[8]建立了表征编织复合材料的RVE模型，并从理论上推导了高温热载荷下的各向异性材料属性的表达式。文献[9]施加温度场于68%纤维体积含量的RVE模型上，将得到的纤维和基体热应力进行体积平均，进而得到各组分的平均应变，求出的RVE热膨胀系数即是单向复合材料的热膨胀系数。文献[10]用商业有限元软件ANSYS对单向纤维增强的复合材料进行建模，计算得到复合材料轴向与横向热膨胀系数。

综合以上的文献，对于热膨胀系数的计算，现在常用的有限元模型一般是先假设截面纤维呈某种形式的分布，然后再取出其中的部份RVE来作分析。但目前对热膨胀系数的计算主要集中在单向复合材料轴向或横向热膨胀系数的预测，对于建立复合材料微观材料特性与复合材料结构件热膨胀系数之间的联系，并根据计算得到的热膨胀系数值对复合材料铺层进行优化设计，则未见报道。

本文采用纤维随机分布法生成RVE，通过微观模型计算得到单向复合材料热膨胀系数；建立复合材料结构宏观模型，由微观模型计算得到单向复合材料热膨胀系数对宏观模型进行热稳定性分析。最后，采用本文的方法对某高分辨率对地观测卫星天线支撑结构进行热稳定性设计与分析，为卫星复合材料结构的热稳定性设计提供了工程参考方案。

2 跨尺度热—力耦合优化方法

复合材料桁架结构跨尺度热—力耦合优化方法包括复合材料热膨胀系数跨尺度数值模型以及热—力耦合优化方法，本文研究对象为线膨胀系数。复合材料热膨胀系数跨尺度数值模型以纤维微观性能为输入(包括纤维热膨胀系数及纤维体积含量)，通过RVE模型计算出复合材料热膨胀系数；建立复合材料构件(如圆管、方管等)有限元模型,通过复合材料热膨胀系数及复合材料构件铺层方式得到复合材料宏观热性能，包括纵向及横向热膨胀系数。复合材料热稳定性跨尺度数值模型采用有限元的方法通过纤维的热膨胀系数得到复合材料构件宏观热性能，建立了纤维微观热性能与结构宏观热性能之间的联系，有助于更好地理解复合材料热性能，并可以大幅度减少试验成本。卫星复合材料桁架支撑结构设计时往往需要根据载荷精度的总体要求，通过精度分配给出桁架结构热变形允许的最大值，并以此最大允许变形参数为设计约束，进行桁架结构设计。通过跨尺度数值模型，结合优化算法，在复合材料构件尺寸一定的情况下，可以反算出满足结构热性能指标复合材料铺层。以卫星天线常用的桁架支撑结构为例，约束桁架杆件的纵向热膨胀系数及刚度，通过跨尺度模型建立的复合材料铺层与构件热膨胀系数之间的关系，根据优化算法得到满足约束条件的铺层，指导桁架结构设计。复合材料桁架结构跨尺度热—力耦合优化方法流程如图1所示。

图1 跨尺度热—力耦合优化方法示意Fig.1 Sketch of multi-scale optimizing numerical model

3 跨尺度数值模型及试验验证

3.1 跨尺度模型

在单向纤维增强复合材料中，纤维在横截面上呈现出随机分布的特点，本文采用纤维随机分布算法描述纤维微观分布，该算法采用Matlab编程，通过输入相应的参数，迅速地生成相应的纤维随机分布模型，并以标准文本文件输出扰动后的纤维圆心的位置，提供给有限元前处理软件生成RVE的细观模型。采用纤维随机分布算法生成的四种不同纤维体积含量(30%、40%、50%、60%，涵盖了工程常用的各种复合材料)的代表性体积单元细观有限元模型。由于要同时预测单向复合材料纵向与横向的热膨胀系数，因而RVE需采用3D模型。针对每一个纤维体积含量的复合材料，都建立彼此相互独立的5个RVE模型，并以5个模型预测结果的平均值作为最终的预测结果，得到纤维热膨胀系数。

图2 管件宏观模型 Fig.2 Three-dimensional composite tube

以桁架杆件为例，典型的复合材料管件模型如图2所示，其长度为L，内径为D0，外径为D1。为了计算横向热膨胀系数，数值模型采用3D实体单元，复合材料热膨胀系数由RVE计算得到。对复合材料管件热膨胀性能的模拟采用MSC.Nastran通用有限元软件进行。Nastran中默认的层合材料铺层顺序为沿着单元法向进行铺设，因此需要对划分好的单元的法向方向进行调整，使其厚度方向为管件的半径方向，从而保证有限元模型的铺层顺序与生产管件时的顺序完全一致。根椐热膨胀系数的定义，其大小为在单位温差下的应变。因而采用有限元模拟复合材料管件热膨胀系数时，除了对管件施加无应力位移边界条件外，还需要施加两状态变量，即初始温度T0与末状态温度变量T0+ΔT，其中ΔT=1℃。最终所得到的管件在轴向与径向的应变即为两方向的热膨胀系数。

3.2 试验结果与分析

为验证数值方法的正确性，对复合材料构件进行热膨胀系数试验研究。本文选用卫星常用的M40/TDE85复合材料进行试验研究，通过跨尺度模型由纤维的热膨胀系数计算得到复合材料构件的热膨胀系数。复合材料构件选用航天试验件常用铺层管件1铺层为[±15°]5/90°，管件2铺层为[±15°/0°]2/0°/[±15°]/90°。对于桁架支撑结构，复合材料管件在轴向的热膨胀性能是其最重要的参数之一。

管件1与管件2在轴向热膨胀性能的预报结果与测试结果如图3所示，总体来看，室温下的预测结果比低温与高温下的结果更为准确。两管件的轴向热膨胀性能，除了管件2在低温下的预测结果与测试结果之间的相对误差较大以外，两管件的其他预测结果的相对误差均小于3%。当试验件在高温与低温时，内部会产生热应力，并且在复合材料内部的缺陷位置处会产生应力集中，从而导致复合材料内部在微观结果上出现损伤与破坏，影响复合材料热膨胀性能在宏观上的表现。由试验结果可知，采用本文跨尺度数值模型，可以较为准确地预测出管件热膨胀系数，验证了跨尺度数值模型的正确性。

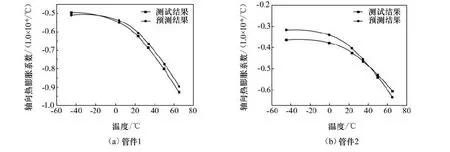
图3 管件轴向热膨胀性能Fig.3 CTE of composite tube

4 热—力耦合优化方法

4.1 优化模型

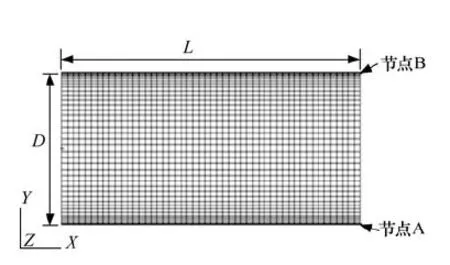
图4 圆管优化模型 Fig.4 Optimized model of composite tube

卫星桁架支撑结构设计时往往需要根据载荷精度的总体要求，通过精度分配给出桁架结构热变形允许的最大值，并以此最大允许变形参数为设计约束，进行桁架结构设计。桁架复合材料杆件需要对其轴向的热膨胀性能进行定量设计以满足工程需求;同时也有对杆件在横向热膨胀性能的要求以匹配管件的接头;对于复合材料杆件轴向的刚度往往也有要求，因其可影响杆件所组成的桁架结构的振动频率及外力作用下的变形等。复合材料杆件的尺寸如图4所示，假定其温差为ΔT，则优化模型的三要素定义如下：

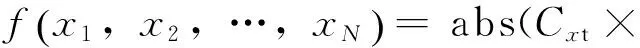
设计变量：各铺层的角度xi,i=1,2,…,N。

图5 热膨胀性能定量优化设计流程 Fig.5 Optimization flow chart

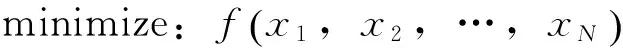
4.2 桁架结构热稳定性分析

采用跨尺度热—力耦合设计方法对文献[11]中复合材料桁架结构进行热稳定性分析。文献中的卫星搭载一台合成孔径雷达(SAR)，其可展开支撑结构采用复合材料管件，天线基板材料与管件材料一致。对天线桁架结构每一根管件在轴向的热膨胀性能进行定量优化，以保证雷达天线阵列在各种温度环境下都具有很高的平面性，使整个桁架结构有很高的尺寸稳定性，从而使得该卫星具有较高的对地观测精度。天线在室温(23℃)下组装，在运行过程中经过环控后管件所经历的最高温度为70℃，最低温度为-50℃，分别定义其为高温环境与低温环境。高温及低温环境下位移云图分别如图6、图7所示，天线整体结构在两种温度环境下的最大位移与其分量如表1所示。

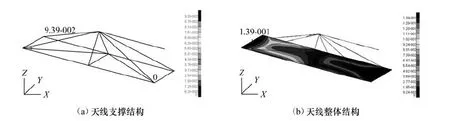
图6 天线整体结构高温环境位移云图Fig.6 Displacement under high temperature of antenna structure

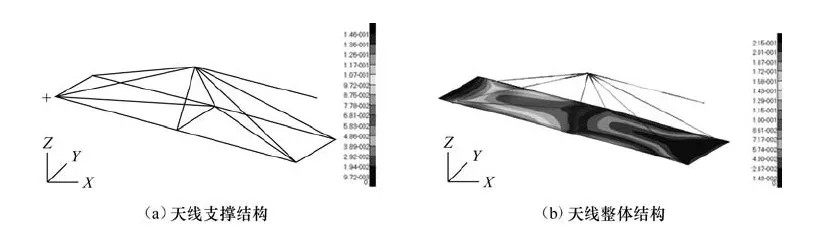
图7 天线整体结构低温环境位移云图Fig.7 Displacement under low temperature of antenna structure

类别最大位移X分量/mm最大位移Y分量/mm最大位移Z分量/mm最大位移/mmX向变形率/%Y向变形率/%Z向变形率/%桁架高温0.09020.02250.03190.09390.14420.15030.1065桁架低温0.14000.06540.04960.14850.22400.43620.1654天线高温0.13740.08560.03330.13900.21980.57090.1110天线低温0.21300.13300.05180.21500.34080.88670.1727

在高温与低温环境下，天线支撑结构与天线整体结构的变形量都很小，最大变形位移小于0.3mm，天线的结构稳定性表现很好。天线整体结构的位移比天线支撑结构大了一倍左右，其原因在于虽然天线支撑结构能保证很小的位移形变，但是天线基板的外侧为自由状态，当天线支撑结构有一很小的转动角度时，其自由端将会由于转动而产生较大的位移。天线与支撑结构在低温环境下产生的变形量大于高温环境下的变形量，原因在于从室温到低温环境下的温差大于室温到高温环境下的温差。根据天线的结构尺寸，可计算出天线在各方向的形变率，从表1中可以看出，天线在长度(X)方向与宽度(Y)方向的最大形变率小于0.01%，而厚度(Z)方向的形变率则小于0.2%。天线形状的高保持率对于SAR等系统的正常运行至关重要。参考RADARSAT-2的技术资料，其天线支撑结构的最大热变形为0.70 mm。经过本文优化出的天线支撑结构的最大变形为0.215 mm，其热变形量远小于RADARSAT-2天线支撑结构的指标，因而可认为经过本文优化出的支撑结构可完全满足卫星天线的使用要求。

5 结束语

本文建立了复合材料桁架结构跨尺度热—力耦合优化设计方法，由复合材料热膨胀系数跨尺度数值模型及热—力耦合优化方法两部分组成。复合材料热膨胀系数跨尺度数值模型通过纤维微观性能，借鉴RVE的方法计算出单向复合材料热膨胀系数；通过建立复合材料构件有限元模型，结合复合材料铺层得到宏观热膨胀系数。复合材料热稳定性跨尺度数值模型建立了纤维微观热性能与结构宏观热性能之间的联系，有助于更好地理解复合材料热性能，并可以大幅度减少试验成本。通过跨尺度数值模型为基础，引入优化算法，在复合材料构件尺寸一定的情况下，反算出满足结构热性能指标的复合材料铺层。本文跨尺度热—力耦合优化设计方法为卫星复合材料结构的热稳定性设计提供了工程解决方案。

[1] 袁家军.卫星结构设计与分析[M].北京：中国宇航出版社，2004:6-20.

YUAN JIAJUN. Design and analysis of satellite structures [M]. Beijing: China Astronautic Press，2004：6-20.

[2] 刘国青，阮剑华，罗文波，等.卫星高稳定结构热变形分析与试验验证方法研究[J].航天器工程，2014，23(2)：64-70.

LIU GUOQING, RUAN JIANHUA, LUO WENBO, et al. Research on thermal deformation analysis and test verification method for spacecraft high-stability structure[J].Spacecraft Engineering，2014，23(2)：64-70.

[3] 麻慧涛，李劲东.大型复杂空间结构机—热集成分析技术研究[J].宇航学报，2008，29(2)：413-419.

MA HUITAO，LI JINDONG. Integrated thermal-structural analytical technology for space structure with large-scale and complicated construction [J]. Journal of Astronautics, 2008，29(2)：413-419.

[4] ISLAM MDR, SJÖLIND SG, PRAMILA A. Finite element analysis of linear thermal expansion coefficients of unidirectional cracked composites [J]. Journal of Composite Material，2001，35(19)：1762-1776.

[5] RUPNOWSKI P，GENTZA M，SUTTERB J K，et al. An evaluation on the elastic properties and thermal expansion coefficients of medium and high modulus graphite fibers [J]. Composites: Part A, 2005，36(3)：327-338.

[6] SHEN Y L.Thermal expansion of metal-ceramic composites: a three dimensional analysis [J]. Materials Science & Engineering A，1998，252(2)：269-275.

[7] SOHEIL MOHAJERJASBI， HELICOPTER DIVISION. Prediction for coefficients of thermal expansion of 3-D braided composites[R].AIAA paper，1996：1812-1817.

[8] JIM LUA，JAG SANKAR，DEVDAS PAI. A four cell decomposition model for unbalanced woven fabric composites subjected to thermal-mechanical loading[R]. AIAA paper, 2006：1-22.

[9] 熊璇，吕国志，吕毅. 细观力学法预测单向复合材料的有效热膨胀系数[J]. 强度与环境，2008，35(2)：24-30.

XIONG XUAN，LV GUOZHI，LV YI. Predicting macroscopic thermal expansion coefficient of unidirectional composite matrial micro-mechanics[J].Structure & Environment Engineering，2008，35(2)：24-30.

[10] KARADENIZ Z HAKTAN，KUMLUTAS DILEK. A numerical study on the coefficients of thermal expansion of fiber reinforced composite materials [J]. Composite Structures，2007，78(1)：1-10.

[11] MORENA L C，JAMES K V，BECK J. An introduction to the RADARSAT-2 mission [J]. Canada Journal-Remote Sensing，2004，30(3)：221-234.

马 健 1985年生，2013年获北京航空航天大学飞行器设计专业博士学位，工程师。研究方向为卫星总体设计。

(编辑：车晓玲)

Thermal-mechanical Optimizing Analysis on Multi-scale Numerical Model for Composite Structure of Satellite

MA Jian1ZHANG Hongyu1YAN Liang1RAN Zhiguo2

(1 Beijing Institute of Spacecraft System Engineering，Beijing 100094) (2 Beijing Institute of Mechanical Equipment，Beijing 100854)

When spacecraft works, it will suffer different temperature environments, while temperature difference will always introduce changes of shape and size of composite structures. However, some spacecraft parts need high dimensional stability to keep its right function. Till now, the mechanical properties of the composite have been widely studied, however, the thermal properties of composite and optimization of composite considering both thermal and mechanical properties are far from well studied.Composite tubes were optimized to a given coefficient of thermal expansion (CTE), and the stiffness of those tubes was taken into consideration at the same time. Firstly, multi-scale numerical models were developed to calculate the CTE. In micro-scale mode, the CTE of unidirectional fiber reinforced composite was calculated by the fiber CTE through representative volume elements(RVE). In macro-scale, a composite tube model was generated to predict both axial and transverse CTE of the tube based on the CTE computed by RVE. Composite laminates and tubes with given plies were analyzed and tested. Comparison between the predicted results and the experimental one verified the model, which made the foundation for the optimization mode. Secondly, optimization models for composite truss structure were created. The conjugate gradient method was adopted to optimize the plies of composite parts, and the thermal-mechanical optimizing method was developed. Finally, the satellite support truss structure was analyzed by the thermal-mechanical optimizing method. Analyzed results show that this optimized support structure and the whole antenna have an excellent thermal dimensional stability. The thermal-mechanical optimizing method can be used for thermal stability design and analysis of composite support truss structures.

Truss；Multi-scale；Optimizing design；Thermal stability；Representative volume element；Coefficient of thermal expansion；Satellite

国家重大科技专项工程资助项目

2014-12-12。收修改稿日期：2015-05-20

10.3780/j.issn.1000-758X.2015.04.005