空间机器人加注机构碰撞力建模与柔顺控制

张海博 王大轶 魏春岭

(1北京控制工程研究所，北京100190) (2空间智能控制技术重点实验室，北京100190)



空间机器人加注机构碰撞力建模与柔顺控制

张海博1,2王大轶1,2魏春岭1,2

(1北京控制工程研究所，北京100190) (2空间智能控制技术重点实验室，北京100190)

为削弱在轨加注过程中主被动端碰撞冲击对空间机器人的影响，提出了基于力/位混合的柔顺控制律。首先通过第二类拉格朗日方程建立了漂浮基座空间机器人一般运动学模型和考虑环境接触的动力学模型。其次，设计了“杆-锥式”加注主被动端装置，根据主被动端的接触特点，建立了点面接触的碰撞动力学模型，并给出相应的碰撞力计算方法。接着，将加注对接问题转化为以基座为参考系的末端运动控制问题，得到了机械臂关节期望运动规律，进而设计了位置环控制律；根据加注主被动端的位置关系计算得到碰撞力，进而设计了力/力矩环控制律，结合顺应选择矩阵最终得到力/位混合控制器，以减小杆锥对接时碰撞对空间机器人基座及末端的冲击影响。最后，仿真结果表明，对接方向的位置误差由初始值降至零，对接过程碰撞产生的力不超过10 N，满足末端工具冲击承载。各关节角度变化平缓，关节力矩不超过13 Nm，满足机械臂关节力矩最小承载，所设计的控制器使得加注主被动端完成柔顺对接。

在轨加注；杆-锥式模型；碰撞模型；碰撞力；力/位混合控制；空间机器人

1 引言

目前在轨或在研的地球同步轨道通信卫星的寿命主要取决于携带的用于轨道保持和姿态控制的推进剂的多少，一旦推进剂耗尽，航天器就失去控制而失效。对于高价值的航天器来说，失效会造成很大的经济损失。在轨推进剂补给[1]能有效延长航天器的在轨使用寿命，并能够节省空间任务成本。正因为如此，利用空间机器人携带空间操作结构对目标航天器进行在轨推进剂补给已成为各国航天技术研究的主要方向之一。美国、俄罗斯及欧洲航天局目前已开展了大量的工作[2]。尤其是美国，在2007年通过轨道快车计划[3]完成了肼燃料的在轨补给，2012年又联合加拿大航天局在国际空间站上相继完成了机器人燃料加注任务技术演示验证的三项重要试验。我国近年来也开展了空间机器人在轨服务技术的研究，取得了一定的成果，并进行了空间机器人在轨加注的地面物理试验。

力/位混合控制是一种直观且概念清晰的柔顺控制方法，它将机械臂末端坐标空间分解成对应于位控方向和力控方向的两个正交子空间，在相应的子空间分别进行位置控制和接触力控制以达到柔顺控制的目的。针对在轨替换单元装配过程，文献[4]提出了一种改进的力位混合控制方法，采用加权选择矩阵代替经典力/位混合控制中原有的选择矩阵，实现了位置、力混合控制的平滑切换。在避免碰撞力过大而损坏设备方面，阻抗控制也是常用到的柔顺控制方法之一，文献[5]中提出了阻抗控制用来处理机械臂和环境的动力学耦合；文献[6-7]研究了空间机器人和非合作目标星之间的接触运动，利用阻抗匹配法给出了始终接触目标和推离目标两者之间的标准，通过两个机械臂模拟服务星和目标星来进行地面试验。文献[8]研究了空间站大臂舱段转移对接过程中的阻抗控制。文献[6-8]中将接触力动力学看作作用在机械臂末端上的脉冲力，然而，实际中碰撞接触模型更加复杂。文献[9]分析了机械臂抓捕目标的碰撞动力学及运动学模型。文献[10-11]建立了基于Simulink的卫星对接仿真器，可以模拟接触力的特性，诸如冲击、弹跳、滑动、旋转、粘滞和阻滞。文献[12]利用仿真器验证了微重力接触动力学。文献[13]提出了捕获过程中减小冲击效应的算法。文献[14]研究了空间机器人应用方面的接触动力学。根据已知的几何和末端执行器，以及抓捕装置的状态可估计接触力的方向，利用估计的接触力和目标运动的观测值得到优化的捕获时间和位置，这使得捕获时物理接触对操作平台姿态的影响最小。虽然文献[9-14]中详细分析了机械臂末端与目标复杂的碰撞过程，但是没有给出合适的控制律来保证碰撞过程的柔顺接触，仅从机械臂抓捕构型的角度给出了抓捕碰撞力最小的抓捕构型。

本文针对空间机器人在轨加注任务，建立机械臂末端加注主动端与被动端碰撞模型，提出一种基于力/位混合控制的柔顺捕获方法。该方法对空间在轨加注任务的实施具有一定的工程借鉴意义。

2 空间机器人运动模型

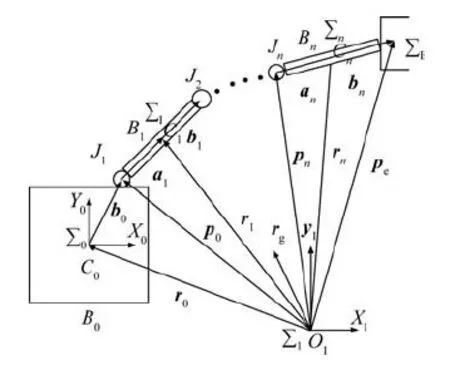
图1 空间机器人一般模型 Fig.1 General model of space robot

空间机器人由作为基座的航天器平台及n自由度串联机械臂组成，机械臂末端可更换不同的操作工具以完成特定的空间操作任务。空间机器人一般模型如图1所示。图1中的符号定义如下：∑I为惯性坐标系，∑0为本体坐标系，∑i为与关节i固联的坐标系(i=1,2,…,n)，∑E为末端坐标系。

根据多体动力学建模思想，得到空间机器人一般运动学方程如下：

式中vb和ωb分别为基座的线速度矢量和角速度矢量；ve和ωe分别为机械臂末端的线速度矢量和角速度矢量；Jb和Jm分别为与基座、机械臂运动相关的雅可比矩阵。

采用拉格朗日法建立系统的动力学模型，当机械臂末端不与环境接触时，具有如下形式：

3 主被动加注端碰撞力计算

3.1 碰撞模型

本文针对空间机器人在轨加注过程，建立加注对接口主被动端的接触碰撞力模型。设计了杆锥式加注主被动端系统，从对接易于实现、可靠性高等方面考虑，试验中选取了圆头形对接杆(轨道快车加注端也是类似的机构)，导引槽有一定的容差，所选对接机构截面如图2所示。

在对接杆向对接孔运动过程中，不断判断主动端插杆边缘处与被动端对接孔壁的位置关系，以嵌入角的形式判断杆与对接孔壁之间是否发生碰撞。如图2所示，φ为插杆边缘对于对接孔壁的嵌入角，当插杆一边嵌入对接孔壁后，φ<0，表明碰撞发生；φ>0表示未发生碰撞。在本模型中，加注主动端安装在机械臂末端，加注被动端安装在目标航天器上，假设在加注主被动端对接前，空间机器人与目标航天器通过某种装置固连在一起，即空间机器人与目标航天器的组合体称之为加注机械臂的基座，并且假设组合体的质量特性已知，坐标系关系如图3所示。机械臂携带对接杆沿基座坐标系Y方向运动，因此在X和Z方向均可能发生碰撞，须在X和Z方向分别进行碰撞力计算。

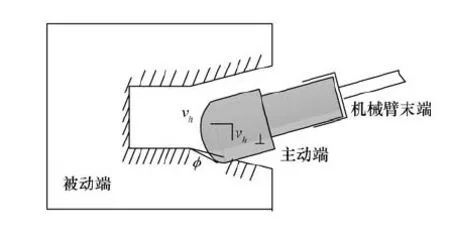
图2 主被动端截面示意Fig.2 Sketch of active and passive device section

图3 碰撞力判断示意Fig.3 Sketch of impact force judgment

如图3所示，可将加注过程的主被动端对接过程分两部分。首先主动端对接杆与被动端对接孔锥形碗面进行接触，然后由对接孔对杆进行捕获。二者的碰撞原理是一样的，不同之处在于对接结构的初始状态及对接孔楔形角的角度大小。

图4 碰撞判断示意 Fig.4 Sketch of impact force judgment

由于对接杆为圆形头部，与接收锥的碰撞为点面接触，因此可将对接杆简化为机械臂末端的质量点，将对接孔简化为X和Z方向具有相同楔形角的锥形碗面。锥形碗面的顶点设置在实际对接孔的中心部位，作为接触过程的结束点，当机械臂末端点与结束点重合时，视为接触过程完成。通过识别末端质量点在锥形槽中的位置进行碰撞判断。将末端质量点投影到锥形碗面坐标系中，如图4所示，令末端质量点到安装结束点的向量为RPE，以X方向碰撞判断为例，将RPE分解为X和Y方向分量，则向量RPE与锥形槽中线的夹角为

φ

令锥形碗面楔形角为θ，若φ>θ，则嵌入量δ>0，发生碰撞，反之未发生碰撞。

这里需要强调一下，对接孔末端对杆的捕获过程，原理与对接杆和对接孔锥形碗面接触过程一致。

3.2 碰撞力计算

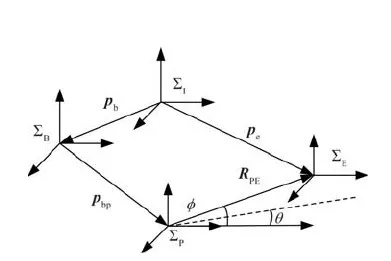
图5 碰撞点空间位置 Fig.5 Position of impact point

碰撞力计算过程将投影在接触过程结束点坐标系下完成，将基座本体系平移至接触过程结束点，并在此系下表示各向量关系，如图5所示。

根据图5中向量的几何关系，得到末端质量点到安装结束点的向量在基座坐标系下的表示为

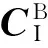
图6 碰撞力示意 Fig.6 Sketch of impact force

如图6所示，碰撞力由两部分组成，垂直于对接孔锥形壁的直碰力及沿对接孔锥形壁方向的摩擦力，直碰力的方向与质量点嵌入方向相反，摩擦力方向与质量点运动方向相反，即对接时摩擦力沿对接孔锥形碗面向外。因此碰撞力fe可表示为

式中 直碰力fn包含有X和Z方向的碰撞力，由赫兹弹性力模型计算得到，则有

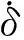
δ=|RPE|sin(φ-θ)

定义n为法向直碰力方向向量，h为中线向量，则有

令μ为摩擦因素，t为切向向量，则摩擦力为

因此碰撞力最终表达式为

通过以上计算方法可以模拟计算出加注主被动端对接过程中的接触力。

作用力矩τe可以由接触力fe与接触点相对于机械臂末端质心的力臂矢量re叉乘计算得出，即

通过以上计算方法可以模拟计算出加注主被动端对接过程中碰撞力和力矩。

4 主被动端对接力/位混合控制

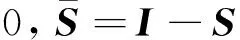
4.1 机械臂末端位置控制

本文中当机械臂末端携带加注主动端与被动端对接时，空间机器人与目标是固连的，也就是说对于对接杆与被动端进行对接的过程，加注被动端在基座坐标系下的位置是固定不变的，即末端期望位姿在基座坐标系下的表示不受基座运动的影响，该问题可描述为以基座为参考系的末端运动控制问题[15]，因此该机械臂的运动学方程可表示为

式中0ve，0ωe为末端速度在基座坐标系下的表示。

在力位混合控制中，通过加权选择矩阵S确定哪些自由度需要进行位置控制，相应的，期望关节角速度为

得到期望关节角速度后，可采用一步欧拉积分来得到期望关节角。给定积分时间间隔为Δt，即控制采样周期。如果关节角和关节角速度在tk时刻是已知的，则在tk+1时刻的值为

式中Kpp和Kpd是可设计的控制器参数，且为对角矩阵，各对角元素均大于零。

4.2 机械臂末端力控制

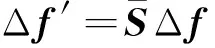
式中Kf p和Kf d是可设计的控制器参数，且为对角矩阵，各对角元素均大于零。

综上，式(3)中的关节控制力矩τm由关节位置PD产生的τp及关节力/力矩PD产生的τf组成，即τm=τp+τf。

5 模型仿真验证

5.1 仿真条件

针对空间机器人自主对接过程，设置材料特性、几何参数及控制参数进行仿真。每个刚体质心在其几何中心，主要特性参数如下：

材料特性：碰撞刚度Kc=104N/m，碰撞阻尼Cc=10 Ns/m，摩擦因素μ=0.2。

几何参数：接收锥楔角θ=27°，对接孔深h=0.2 m，锥楔角为零。

机械臂末端工具冲击承载≤20 N；关节力矩最小承载≤30 Nm。

初始参数：基座位置及速度均为0，各关节速度均为0，初始末端速度为0。

基座质量：m0=2 048 kg。

各连杆质量：m1～6=[2.2 17.6 10.1 7.0 10.1 11.9]kg。

各连杆惯量矩阵：

机械臂运动学参数如图7所示。

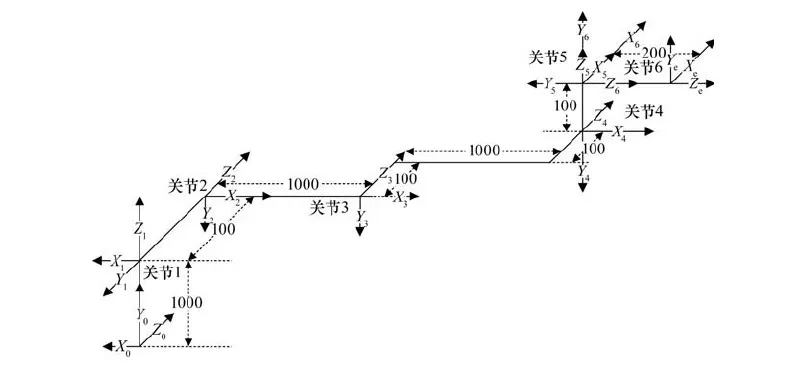
图7 六自由度机械臂D-H坐标系Fig.7 D-H frames of 6 degree of freedom manipulator

5.2 对接过程仿真分析

图8 基座位置变化曲线 Fig.8 Change curve of base position

在仿真条件下，设置对接杆位于接收锥边缘，末端质量点距接触过程结束点仅存在Y方向偏差0.35 m，距捕获过程结束点仅存在Y方向偏差0.20m。利用操作空间控制使杆向对接孔内运动，期间加注主动端先与接收锥壁发生碰撞，然后被对接孔捕获，发生碰撞。碰撞力作用于机械臂末端和基座上，应用力/位混合控制器公式(17)、(18)，所得杆-锥对接过程仿真结果如图8～图12所示。

由仿真结果知，Y方向位置误差由0.55m降至0m，其中0.55m～0.20m段为对接杆与接收锥的碰撞阶段，中间有个转折，说明对接杆与接收锥有两次碰撞；0.2m～0m段为对接杆被对接孔捕获阶段，开始有小幅下降，然后误差变大，说明对接杆在对接孔中心位置移动，然后触碰到对接孔臂，受到碰撞力影响反弹，最后在机械臂控制下仍慢慢滑入对接孔壁，直至完成对接。在对应的说明处时X和Z方向几乎无误差，说明对接过程成功完成。对接过程碰撞产生的力不超过10N，X方向力较大，Z方向力很小，说明对接杆插入时紧贴X方向一侧对接孔壁滑入，Y方向力随X方向碰撞力变化，说明对接杆与对接孔壁之间存在较大摩擦力。各关节角度变化平缓，关节力矩不超过13Nm。

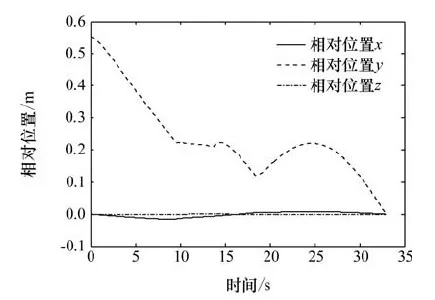
图9 对接杆末端与接收锥结束点间相对位置Fig.9 Relative position between the docking pole end-effector and the receiving cone end point

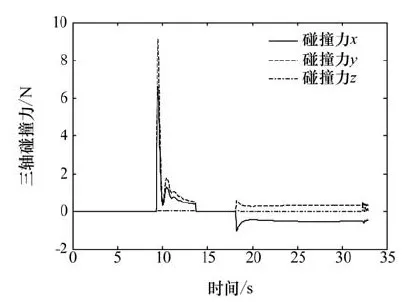
图10 加注主被动端接触过程中三轴碰撞力Fig.10 Three axis impact force in process of refueling active and passive device contact

图11 关节角度变化曲线Fig.11 Change curves of joint angles

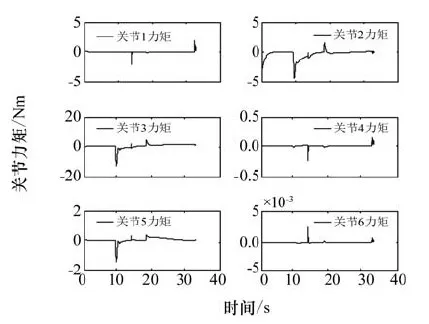
图12 关节力矩变化曲线Fig.12 Change curves of joint torques

6 结束语

随着空间机器人及其在轨服务技术的发展，通过在轨加注以增强航天器功能或延长其寿命将成为可能。本文针对比较普遍应用的“杆-孔插拔式”加注主被动端模型，分析了主动端对接杆与被动端对接孔锥形碗面的接触特点，并提出了相应的接触力计算方法，应用力/位混合控制，减小碰撞冲击对空间机器人的影响。由于碰撞接触模型与接触面的外形及材料等有关，未来将针对各种典型情况下非合作目标抓捕操作过程中的碰撞问题开展动力学建模、力/位混合控制方法的深入研究，并建立试验系统，进行试验验证。

[1] 于洋, 丁凤林, 宗光华. 在轨加注用超声波流量计的设计与试验[J]. 中国空间科学技术, 2014，34(4)：77-83.

YU YANG, DING FENGLIN, ZONG GUANGHUA. Design and test of an ultrasonic flow meter for orbital refueling[J]. Chinese Space Science and Technology，2014，34(4)：77-83.

[2] 何英姿, 魏春岭, 汤亮. 空间操作控制技术研究现状及发展趋势[J]. 空间控制技术与应用，2014，40(1)：1-8.

HE YINGZI, WEI CHUNLING, TANG LIANG.A survey on space operations control[J]. Aerospace Control and Application，2014，40(1)：1-8.

[3] FRIEND R B. Orbital express program summary and mission overview[C]. Sensors and Systems for Space Applications II，Orlando，FL，March 17-18，2008.

[4] 徐文福，周瑞兴，孟得山. 空间机器人在轨更换ORU的力/位混合控制方法[J]. 宇航学报, 2013，34(10)：1353-1361.

XU WENFU, ZHOU RUIXING, MENG DESHAN. A hybrid force/position control method of space robot performing on-orbit ORU replacement[J]. Journal of Astronautics，2013，34(10)：1353-1361.

[5] HOGAN N. Impedance control：an approach to manipulation[J]. ASME Journal of Dynamic Systems，Measurement & Control，1985，107：1-24.

[6] YOSHIDA K，NAKANISHI H. Impedance matching in capturing a satellite by a space robot[C].IEEE/RSJ International Conference on Intelligent Robots and Systems，Las Vegas，Evada，2003：3059-3064.

[7] YOSHIDA K，NAKANISHI H，UENO H，et al. Dynamics, control and impedance matching for robotic capture of a non-cooperative satellite [J]. Advanced Robotics, 2004, 18(2): 175-198.

[8] 危清清，刘志全，王耀兵，等. 柔性机械臂辅助空间站舱段对接阻抗控制[J]. 中国空间科学技术, 2014,34(6):57-64.

WEI QINGQING，LIU ZHIQUAN，WANG YAOBING，et al. Impedance control of space flexible manipulator system assisted docking of space station [J]. Chinese Space Science and Technology，2014，34(6)：57-64.

[9] CYRIL X. Post-capture dynamics of a spacecraft-manipulator-payload system [J]. Journal of Guidance， Control and Dynamics，2000， 23(1)：95-100.

[10] CARR R，MA O，YANG G，et al. A Simulink-based satellite docking simulator with generic contact dynamics capabilities[C]. The 6th International Symposium on Artificial Intelligence，Robotics， and Automation in Space(i-SAIRAS)，Montreal，Canada，2001.

[11] MA O. Envelopment and applications of a Simulink-based satellite docking simulator with generic contact dynamics capabilities[C]∥Proceeding of 2002 IAF World Space Congress， Houston，TX，2002:10-19.

[12] DIAO X，MA O，LIU M. Dynamics of a robotics-based hardware-in-the-loop simulator for verifying microgravity contact dynamics[C]∥Proceeding of SPIE, Modeling，Simulation，and Verification of Space-based Systems III，Orlando，Fl，2006.

[13] MA O，FLORES-ABAD A，PHAM K. Control of a space robot for capturing a tumbling object [C]. International Symposium on Artificial Intelligence，Robotics and Automation in Space，I-Sairas，Turin，Italy，2012.

[14] KRENN R, HIRZINGER G. Contact dynamics simulation for space robotics applications[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems，Nice，France，September 22-26，2008.

[15] PAPADOPOULOS E, DUBOWSKY S. On the nature of control algorithms for free-floating space manipulators [J]. IEEE Transactions on Robotics and Automation，1991，7(6)：750-758.

[16] SCIAVCCO L, SICILIANO B. Modelling and control of robot manipulators [M]. London: Springer，2000：120-124.

张海博 1983年生，2013年获哈尔滨工业大学控制科学与工程专业博士学位，工程师。研究方向为空间机器人操作控制，航天器姿轨协同控制。

(编辑：车晓玲)

Contact Dynamics Model of Refueling Device and Compliance Control for Space Robots

ZHANG Haibo1,2WANG Dayi1,2WEI Chunling1,2

(1 Beijing Institute of Control Engineering，Beijing 100190) (2 Science and Technology on Space Intelligent Control Laboratory，Beijing 100190)

Force/position hybrid compliant control law was proposed to weaken the effect on space manipulator when an active device was involved in a collision with a passive device. Firstly，using the second kind of Lagrange equations，the floating base space manipulator kinematics and dynamics model were constructed considering the contact environment. Secondly，a pole-cone type refueling device was given. According to the contact characteristics of the active and passive device，a point-surface contact collision dynamics model was established，and the corresponding collision force calculation method was given. Then，refueling docking problem was formulated for spacecraft-referenced end-point motion control problem. On this basis，the desired manipulator end-point trajectory was planned and the position loop control law was proposed. The collision force was obtained according to the position between the refueling active and passive devices，and the force/torque loop control law was proposed. Furthermore，combined with adaptation selection matrix，the force/position hybrid controller was obtained to reduce the collision impact on space robot. Finally，simulation results show that the docking direction position error reduces to zero from the initial value，and the collision force is less than 10 N during docking，and joint torque does not exceed 13 Nm. The active and passive devices complete compliant contract by the designed force/position hybrid controller.

On-orbit refueling；Pole-cone model；Impact mode；Contact force；Hybrid force/position control；Space robot

重点实验室基金(9140C590202140C59015)资助项目

2015-04-14。收修改稿日期：2015-05-19

10.3780/j.issn.1000-758X.2015.04.001