电机机座的模态试验与仿真
2015-02-23李名殷
曹 扬,李名殷
(上海电气集团上海电机厂有限公司,上海 200240)
电机机座的模态试验与仿真
曹扬,李名殷
(上海电气集团上海电机厂有限公司,上海200240)
摘要:介绍了对560-2P电机机座结构进行的模态试验和有限元仿真计算,并根据试验结果修正了有限元仿真参数,得到该机座试验和仿真相一致的前5阶固有频率和振型,为电机进一步的振动分析提供了依据。
关键词:机座;模态试验;仿真
0引言
对电机主要零部件进行模态分析和参数识别是进行电机振动和机械噪声控制的主要手段,可以了解现有电机零部件的动力特性,为结构修改和新产品的开发提供开发手段和基础数据。
560-2P电机机座为二侧面弯板薄壁结构,机座上方全部开启。总装时通过其上方放置定子。机座焊接采用特殊工艺,焊后不再进行消除应力处理[1]。焊接残余应力对构件的固有频率有一定影响[2-3],难以精确计算,通过试验方法修正计算模型是目前普遍采用的方法。
以一台560-2P 50 Hz电机机座为对象,进行了结构的模态试验和模态计算,初探有限元模型修正方法,为电机进一步的振动分析提供依据。
1模态试验原理与方法
1.1 模态试验原理[4-6]
模态试验的基本原理是将工程中的连续弹性体振动系统离散成具有n个自由度的线弹性振动系统,用力锤或激振器对系统激振,并同时记录激励和n个自由度方向的响应信号,送入信号分析系统中进行傅里叶变换,获得各测点(自由度)的频响函数,对频响函数进行曲线拟和后得到系统的模态参数。
系统的运动微分方程为:
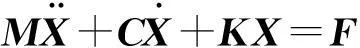
(1)
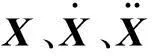
对式(1)进行Fourier变换得到
Z(ω)X(ω)=F(ω)
(2)
式中,Z(ω)=K-ω2M+jωC称为机械阻抗矩阵,其逆矩阵H(ω)=[K-ω2M+jωC]-1称为位移传递函数矩阵,即
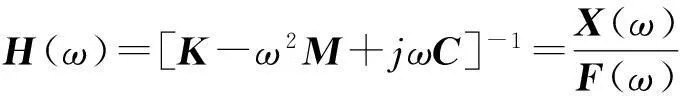
(3)
对于比例粘性阻尼系统,引入坐标变换对方程(1)进行解耦可得传递函数矩阵
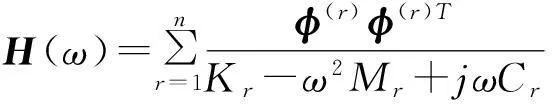
(4)
式中,φ(r)为系统的第r阶模态矢量(振型);Mr、Cr、Kr分别为模态质量、模态阻尼和模态刚度。式(4)的第i行、第j列元素为
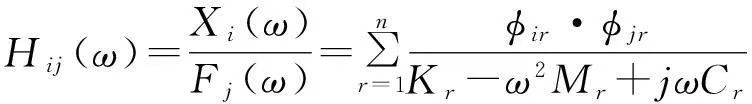
(5)
上式表明,频响函数中的任一行或任一列,包含了系统全部的模态参数信息,这意味着可以通过单点激励多点响应(SIMO)或者多点激励单点响应(MISO)试验,从所得的一列或一行频响函数中辨识得到系统的全部模态参数。
1.2 试验方法
模态试验系统布置图如图1所示。文章采用力锤单点锤击激振多点拾振法(即SIMO方法)测试电机机座的模态。试验采用的仪器设备见表1。
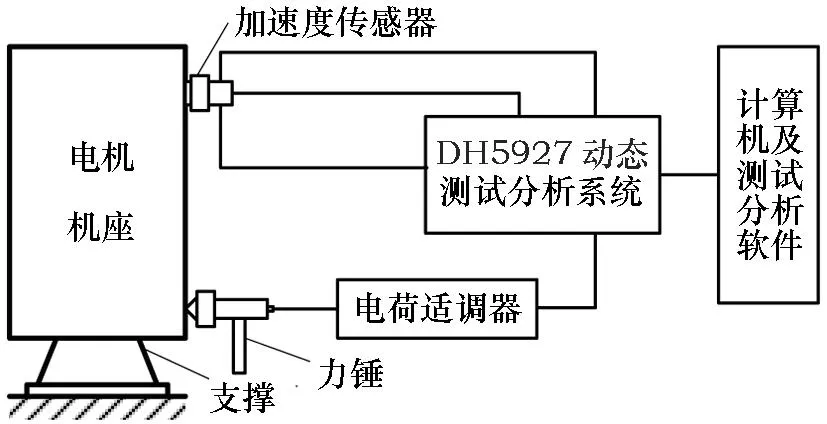
图1 模态测试系统图表1 试验仪器和设备

序号名 称数量生产厂家1DH5927N动态信号测试分析系统32通道江苏东华测试2PCB三向加速度传感器10个美国PCB3250kN力锤1套北京波普4DH5857电荷适调器1个江苏东华测试5笔记本电脑1台联想
机座两端采用木方支撑,如图2所示,木方又置于橡胶垫之上。由于木材和橡胶的刚度远小于机座本身,可近似认为是自由边界。根据机座薄壁结构特征,只要激励点不在各阶模态振型的节点上,并且激励的能量足够大,理论上可以激发出系统的所有模态[7]。因此,采用力锤单点激励,移动传感器的方法能够满足试验要求。

图2 机座的支撑方式
为了确定模态试验中的测点布置和采样频率参数,在试验之前采用FEA软件对机座进行初步模态计算,初步了解结构的固有频率分布范围、模态密集程度,以及各阶模态振型等。根据结构动态特性预估,测点布置示意图见图3,选择4点作为激振点。机座底板的振动为局部振动,不需关注,因此只在机座的外侧板和两端板布置测点。测点总数为106。每个测点用三向加速度传感器采集响应数据,因此总共采集318个响应数据。

图3 测点布置图
2数据采集和参数识别
试验采用10个三向传感器进行共11批次数据采集,共获得318组频响函数曲线,导入DHMA模态分析软件。采用POLYLSCF方法进行参数识别,通过稳态图和振型计算提取了被测机座的前5阶整体模态频率和阻尼比,并通过MAC值校验法验证了试验结果的有效性。试验结果如图4和图5(b)所示。
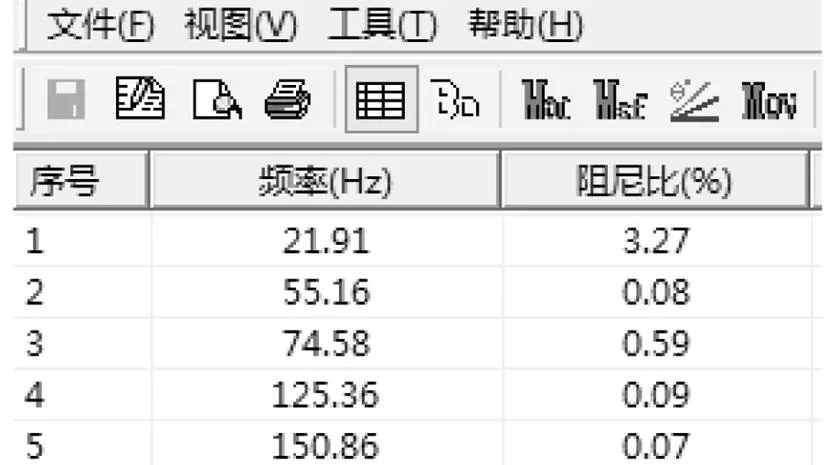
图4 试验模态参数

图5 前5阶模态振型
3机座模态的有限元计算及修正
3.1 模态计算
采用三维建模软件Solid Edge建立了机座的装配体模型,导入ANSYS Workbench中计算机座的固有频率和振型。
机座由Q235-A钢板焊接而成,材料密度为7 850 kg/m3,弹性模量为200 GPa,泊松比为0.3,采用3D单元solid185划分网格。由于ANSYS中的模态分析不支持非线性行为[8],因此采用线性绑定(Bonded)接触,接触刚度及Pinball等参数为系统默认。不计阻尼影响,计算结果见图5(a)和表2。
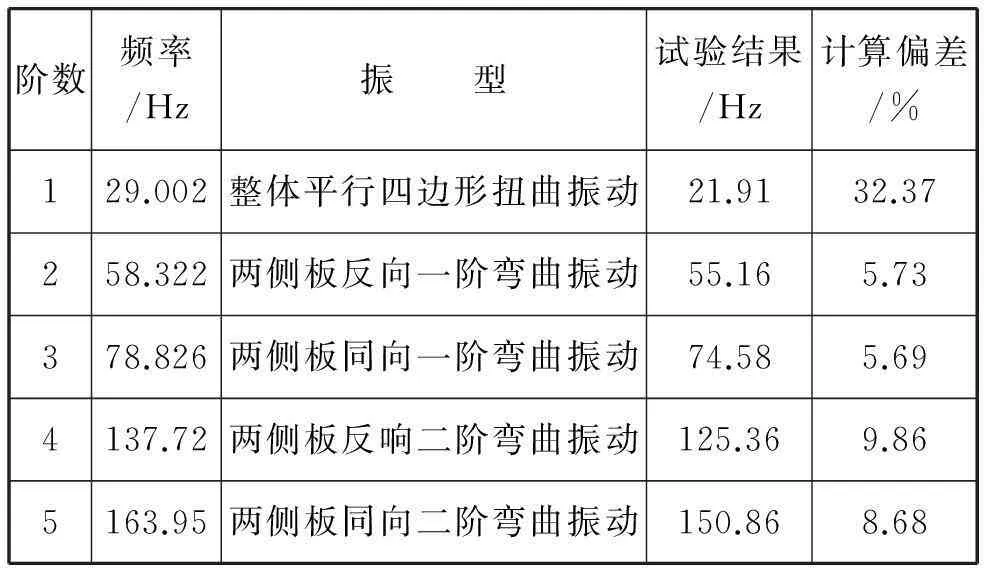
表2 机座有限元模态计算结果
3.2 有限元计算参数修正
有限元的初步计算结果显示,机座结构的一阶频率与实验结果相差较大,而二阶至五阶固有频率与实验值相比偏差均在10%以内。
从各阶振型看,机座的第一阶振型与底脚的约束情况关系很大。在有限元计算中考虑自由模态,因此偏差较大。机座二阶至五阶振型对底脚约束的敏感程度不大,因此偏差较小。
在结构动力学计算中,采用高阶单元通常能获得比采用低阶单元更准确的结果,因此,在有限元计算模型参数修正过程中,采用了solid185的高阶单元solid186进行网格划分。同时,考虑到实际机座结构的部分焊缝为间断焊,并且焊后不经热处理,对模型焊接位置的接触刚度做修正。结果见表3所示。

表3 有限元计算修正与实验结果对比
表3的结果表明,采用合适的单元类型并对主要参数接触刚度进行修正后获得了较好的结果。除一阶频率外,其余几阶固有频率与实验相比偏差不超过5%。第一阶固有频率虽偏差16.84%,但从频率数值上看,偏差并不算大。因此,认为有限元修正参数后的计算获得了与实验一致的结果。
4结语
采用锤击法测量了某560-2P电机机座的固有频率和振型,获得了该机座的前五阶模态参数,并根据试验结果修正了有限元计算结果。
有限元计算结果与试验结果一阶固有频率偏差为16.84%,其余偏差不超过5%,可以认为有限元计算结果较为真实地反映了机座结构的实际模态情况,表明有限元模态算法在该类产品设计中是有效的。
本文的结论可为下一步进行电机整体的结构设计及振动特性分析提供依据。
参考文献
[1] 滕文江. TMEIC电机制造中的工艺特点[J]. 上海大中型电机,2007(4):18-20.
[2] 鲁科明,杨伯荣,贾宝春等. 焊缝型式和焊接残余应力对焊接结构动力参数的影响[J]. 水利电力机械,1990,(06):34-37.
[3] 高永毅,苏志霄,焦群英等. 残余应力对构件固有频率影响的讨论[J]. 机械强度,2002,24(2):289- 292.
[4] [日]大久保信行. 机械模态分析[M]. 上海:上海交通大学,1998.
[5] 许本文,焦群英. 机械振动与模态分析基础[M]. 北京:机械工业出版社,1998.
[6] 俞云书. 结构模态试验分析[M]. 北京:宇航出版社,2000.
[7] 张力等. 模态分析与实验[M]. 北京:清华大学出版社,2011.
[8] 谢龙汉,刘新让,刘文超. ANSYS结构及动力学分析[M]. 北京:电子工业出版社,2012.
