一种基于轮廓波变换的高效率去噪算法研究

李先苦　(长江大学电子信息学院，湖北 荆州 434023)

谢凯　(长江大学电子信息学院，油气资源与勘探技术教育部重点实验室(长江大学)，湖北 荆州 434023)

李纪成，余秋哲，张龙　(长江大学电子信息学院，湖北 荆州 434023)

[引著格式]李先苦，谢凯，李纪成，等.一种基于轮廓波变换的高效率去噪算法研究[J].长江大学学报(自科版)，2015,12(28)：16～20.

一种基于轮廓波变换的高效率去噪算法研究

李先苦(长江大学电子信息学院，湖北 荆州 434023)

谢凯(长江大学电子信息学院，油气资源与勘探技术教育部重点实验室(长江大学)，湖北 荆州 434023)

李纪成，余秋哲，张龙(长江大学电子信息学院，湖北 荆州 434023)

[摘要]为提高地震属性剖面的信噪比和空间分辨率,提出了一种基于轮廓波变换的高效率去噪算法。该方法利用地震剖面能量分布的空间特征,结合9-7正交滤波器组和方向滤波器组对原始采集的地震剖面进行多尺度分解,根据有效地震信号和噪声信号分解后的差异性设计了一种自适应的阈值滤波器,通过拉普拉斯金字塔重构地震数据实现轮廓波变换去噪。试验结果与小波变换算法的去噪结果对比论证表明,基于轮廓波变换的高效率去噪算法能够有效压制噪声,提高地震信号的信噪比,处理后效果较小波变换有明显提高。

[关键词]地震资料;去噪;9-7正交滤波器组;多尺度分解;轮廓波变换

在地震勘探过程中，原始采集的地震信号往往含有大量的随机噪音，这些噪音信号的干扰会降低地震信号的成像质量，因此直接对采集的地震剖面进行分析并不是一个明智的选择。为了获得高分辨率的地震剖面，必须利用有效的技术手段对噪声信号进行处理。目前，在信号处理领域最常用的是傅里叶分析方法和小波变换处理方法[1]。由于地震信号表现出的非线性和非平稳性，导致傅里叶分析方法的去噪效果较差并且处理算法较为冗余，效率较低。在地震信号处理方面，由于地震信号的奇异性主要由边缘和轮廓产生，并且由二维小波张量所构成的小波基函数方向性较差，这直接导致了传统的小波变换在地震信号处理方面的去噪效果也不够明显。

为了较好的处理多维信号的奇异性，多尺度几何分析应运而生。轮廓波变换[2~5]具有良好的多分辨率特性和时频局部化特性[6]以及良好的各向奇异性特征，广泛应用于图像降噪处理。然而，轮廓波变换在对地震数据进行多尺度分解时往往效率比较低，在降噪的过程中对有效信号损伤较大，为了弥补这种缺陷，笔者提出了一种基于轮廓波变换的高效率算法。

1轮廓波变换算法

图1　基于轮廓波变换的高效率去噪算法流程图

图2　9-7正交滤波器组的设计框图

在整个轮廓波变换处理过程中，其核心步骤主要包括拉普拉斯金字塔多尺度分解、方向滤波器组进行方向滤波以及基于9-7正交滤波器组[7,8]进行重构。首先将地震数据导入设计好的拉普拉斯金字塔滤波器[9~12]进行多尺度分解，滤波器组会根据地震数据的结构分布特点进行奇异点的捕获，每次进行分解后得到原始图像分辨率的低通子带和带通子带，对低通子带进行迭代处理实现了原始地震数据的多尺度分解。多尺度分解完后，将带通地震数据利用方向滤波器组合并求出奇异点，进而产生类似于树状的楔形子带，完成了地震数据的多方向分解。轮廓波基函数的支撑区间是一系列适应于各个尺度的长条形，同时兼具方向性和各向异性，对曲线有更稀疏的表达。地震数据在经过轮廓波变换后，有效地震信号的能量主要集中在轮廓波系数的零值附近，而噪音信号的能量则随机分布在所有轮廓波系数上，正是由于2种信号在轮廓波域中表现出的差异性，因此轮廓波变换能有效的去除噪声信号。其具体实现的流程图如图1所示。

1.1　信号的尺度分解

在传统的轮廓波变换过程中，首先利用二维小波滤波器组来对地震数据进行尺度分解，然后使用方向滤波器组把地震数据转换和方向分解，最后按照一定的比例缩放成二维小波基函数[13,14]的地震数据。对廓波变换整个过程的深入研究发现，滤波器组处理效率还有很大的提升余地，并且处理精度还不高。在此基础上，针对地震数据结构和能量分布特点，笔者设计了一种9-7正交滤波器组，如图2所示。图2中， H(z)是分解低通滤波器，G(z)是一个分解高通滤波器，H′(z)是合成低通滤波器，G′(z)是合成高通滤波器，x(n)是输入信号，y0(n)是输出子带信号。

1.2　信号的方向分解

方向滤波器组采用了共轭镜像滤波器组[15,16]的方式，将拉普拉斯金字塔进行多尺度分解所得到的i个子带信号y0(n)进行方向分解，得到2i个并行结构。其中，方向滤波器组一方面能够将二维频谱正交分解，相当于双通道梅花形滤波器组，表现形式主要为扇形滤波器组合，另一方面，某把地震数据打乱实现重排列，进而可以完成各个方向频带的重构。所有采样矩阵与等价滤波器合成的并行通道滤波器组均等价于方向滤波器组。其中，采样矩阵为对角矩阵：

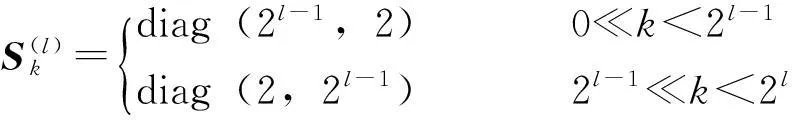
式中，l是尺度；k是方向分解后的子带信号的个数； diag()是取对角矩阵的符号，表明采样过程的独立性。

由各尺度、各方向子带的并行性得到分解后的信号集合y1(n)：

1.3　阈值去噪

对于经过方向分解后得到的子带数据体y1(n)，采用半软阈值函数对其进行去噪处理。半软阈值函数结合了硬阈值和软阈值方法，设有2个大小不同的阈值，保留大于阈值的系数，将小于阈值的系数置零，适当缩减其他的阈值的系数。这样就可以对分解得到的子带进行阈值去噪，得到处理后信噪比有所提高的子带信号y2(n)。其中阈值选取函数C′(j,l,k)如下：

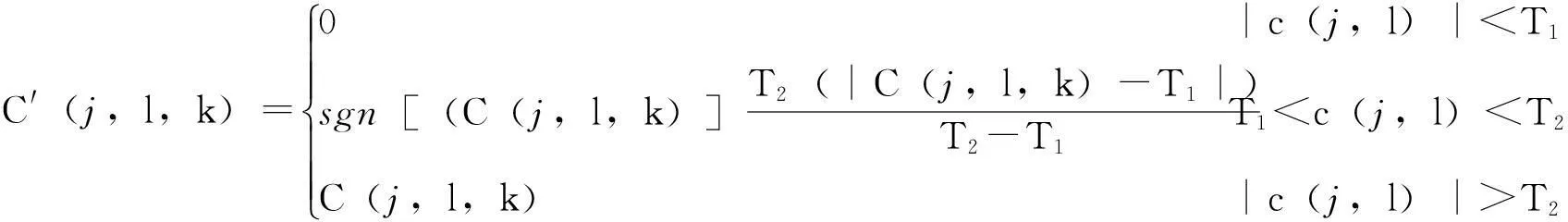
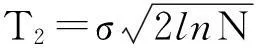
1.4　子带信号的重构

图3　地震数据重构示意图

2试验结果与分析

为了验证算法的可行性，分别利用小波变换、轮廓波变换和基于9-7滤波器组的轮廓波变换来处理仿真模型数据和实际的采集数据，从空间分辨率和能量分布的情况来进行对比论证。试验环境为Matlab仿真软件。

2.1　仿真试验结果验证

根据实际的地震勘探环境，笔者构建了相关的模型数据，其噪音系数为0.015。利用上述3种方法对模型数据进行去噪处理，且均用相同的阈值选取方法。其中小波去噪时选用Haar小波作为母小波，并采用半软阈值函数来进行去噪。对应处理结果如图4所示。

图4　仿真试验结果

图5　单道数据对比图

从图4可以看出，小波变换在去噪过程中，对有效信号的损伤较为严重同时去噪也不彻底，而改进轮廓波变换处理效果比较理想，对处理后的地震数据和原始地震数据做相关分析发现，2者相关度达到了0.84。

2.2　单道数据的分析

对上面3种处理的结果同时抽取第10道地震记录，结果如图5所示。从图5中可以看出，小波变换对其中的一个峰值损害较大，即对有效信号损伤严重，在数据趋向零区域中，前2种方法均在处理过程中反而增加了噪音，去噪效果较差，反观改进轮廓波变换处理结果，在去噪的同时也提高了地震数据的保真度。

2.3　实际工区数据的测试

为了确保算法的准确性，在实际工区采集了10条地震剖面数据，其中一条剖面处理结果如图6所示。由图6可以看出，采用不同的处理方法对地震数据进行去噪处理得到的结果也有较大的差异，轮廓波变换有效保留了地震资料的高频部分，图6 (d)的轮廓信息明显比图6(b)和图6(c)要清晰，证明了改进轮廓波变换对提升地震数据的信噪比有着积极促进作用。

处理前后信噪比的对比结果如表1所示。从表1中可以看出，3种处理方法均对地震数据的信噪比有所提高，其中改进轮廓波处理后的地震数据的信噪比最高，说明了轮廓波变换的可靠性。

图6　实际数据处理结果对比结果

地震剖面编号原始采集地震数据信噪比/dB小波变换处理后信噪比/dB轮廓波变换处理后信噪比/dB改进后轮廓波变换处理后信噪比/dB14.124.565.245.9924.484.755.325.7834.654.765.015.2444.784.825.225.6854.124.325.035.4364.634.705.365.8774.854.885.255.8985.065.525.966.0194.244.364.995.36104.014.254.865.34

3结语

在充分研究了地震数据的噪音来源的基础上，根据其能量分布特点，构建了对应了仿真模型，提出了一种基于9-7滤波器组的改进轮廓波变换算法。在试验论证阶段，分别利用小波变换，轮廓波变换和改进轮廓波变换来处理模型数据和油田采集数据，3种方法对噪音均有压制作用，但小波变换去噪不彻底并且造成了地震数据的较大失真，而轮廓波变换处理结果好于小波变换，但仍然有失真情况。改进轮廓波变换利用了9-7滤波器组保留了大量的有效信号，故处理效果最佳，提高了地震数据的保真度。

[参考文献]

[1]Gao X, Xiao F, Li B.Construction of Arbitrary Dimensional Biorthognal Multiwavelet Using Lifting Scheme[A].IEEE Trans Image Processing[C]. 2009: 942~955.

[2] Do M N. Contourlets and sparse image expansions [J].Proceedings of SPIE Applications in Signal and Image Pro-cessing, 2003，5207(9):560～570.

[3] Do M N，Vetterli M. The contourlet transform: An efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing, 2005，14 (12):2091～2106.

[4] Po D D Y, Do M N. Directional multiscale modeling of images using the contourlet transform [J]. IEEE Transaction on Image Processing,2006,15(6):1610～1620.

[5]Eslami R, Radha H. Image denoising using translation-invariant contourlet transform[A].IEEE International Conference on Acoustics, Speech, and Signal Processing[C].2005:557～560.

[6]Wang Xiangyang，Yang Hongying,Fu Zhongkai.A New Wavelet-based image denoising using undecimated discrete wavelet transform and least squares support vector machine[J].Pergamon Press,2010(37):7040～7049.

[7]Villasenor J D, Belzer B, Liao J. Wavelet filter evaluation for image compression [J]. IEEE Trans on Image Processing, 1995, 4(8): 1053～1060.

[8]刘再德，郑南宁.高性能、有理系数9/7双正交小波滤波器组的设计[J].西安交通大学学报,2005, 39(8):849～851.

[9]黄小丹.基于拉普拉斯金字塔变换的小波域图像融合[J]. 电子科技,2014(6):170～173.

[10]李智勇,邢应春,刘同旭. 基于拉普拉斯金字塔变换的电力图像融合[J]. 计算机系统应用, 2014(9) :563～566.

[11] Bharath A A, Ng J. A steerable complex wavelet construction and its application to image denoising[J]. IEEE Transactions on Image Processing, 2005, 14(7): 948～959.

[12]Li Zhen-hua, Jing Zhong-liang. Remote Sensing ImageFusion Based on Steerable Pyramid Frame Transform[J]. Acta Optica Sinica, 2005,25(5):598～602.

[13]钟建军,宋健,由长喜,等.基于信噪比评价的阈值优选小波去噪法[J]. 清华大学学报(自然科学版),2014(2):259～263.

[14]马博华，郭滨钊，张海成.基于二维正交小波滤波器设计方法[J].计算机仿真,2010(9):220～223.

[15] 何改平. 矩阵共轭镜像滤波器组的设计[J]. 西安邮电学院学报, 2009(3):61～64.

[16] Yoon P S,Cho Nam I K.Design of Signed Powers of Two Coefficient Perfect Reconstruction QMF Bank Using CORDIC Algorithms[A].IEEE Transactions on Circuits and Systems I:Regular Papers[C]. 2006:232～235.

[编辑]洪云飞

[中图分类号]P631.42

[文献标志码]A

[文章编号]1673-1409(2015)28-0016-05

[通信作者]谢凯(1975-)，男，博士，教授，博士生导师，现主要从事油气信息处理和三维地质建模方面的教学与研究工作；E-mail:pami2010@163.com。

[作者简介]李先苦(1993-)，男，硕士生，现主要从事信号处理方面的研究工作。

[基金项目]中国石油创新基金项目(2010D-5006-0304)；长江大学大学生创新创业训练计划项目(2014012)。

[收稿日期]2015-06-12