双循环圆液力缓速器叶形参数优化设计

闫清东，穆洪斌，魏巍，刘树成

(1. 北京理工大学 机械与车辆学院，北京100081;2. 北京理工大学 车辆传动国家重点实验室，北京100081)

0 引言

液力缓速器又称液力减速器，是一种常用的车辆辅助制动装置。作为典型的液力元件，液力缓速器以其制动功率密度大、制动平稳、制动持续时间长等优点，在重型车辆中得到广泛应用［1］。

双循环圆液力缓速器具有制动功率大，径向尺寸小等优点，多用在大功率轮式车辆上［2-3］。其叶片多采用弯叶片结构，叶片整体呈轴向弯曲状，工作面与垂直轴面夹角约为90°角，避免了叶片间的相互遮盖，铸造过程中的拔模工艺较直叶片得到简化，并利于动轮压力平衡孔的加工，图1 为某双循环圆液力缓速器叶轮结构图。

图1 双循环圆液力缓速器结构简图Fig.1 Structure of dual torus hydraulic retarder

液力缓速器的叶栅结构直接决定了其制动性能，而通常对于叶栅结构的优化设计可从循环圆与叶形两个方面开展研究。通过增大循环圆轴向与径向尺寸均能有效提高缓速器的制动力矩［4］，但须以牺牲有限的车内传动空间为代价。因此，在不改变循环圆尺寸的前提下，开展叶形结构优化才是叶栅系统优化设计的关键。目前，国内学者对等厚直叶片做了一定的优化研究。文献［5-6］开展了多参数对制动力矩共同作用的优化研究，提高缓速器的制动性能。文献［7-9］采用参数建模方法对叶形参数进行优化设计，揭示了各叶形参数对制动力矩的影响。

本文针对双循环圆液力缓速器弯叶片，基于参数化设计方法与网格独立性验证，搭建了优化设计仿真平台。结合试验设计、近似模型及全局优化算法［10］，对弯叶片叶形参数开展优化设计研究。

1 几何模型

弯叶片工作面与背面在轴面(x-y 面)投影曲线，如图2 所示。

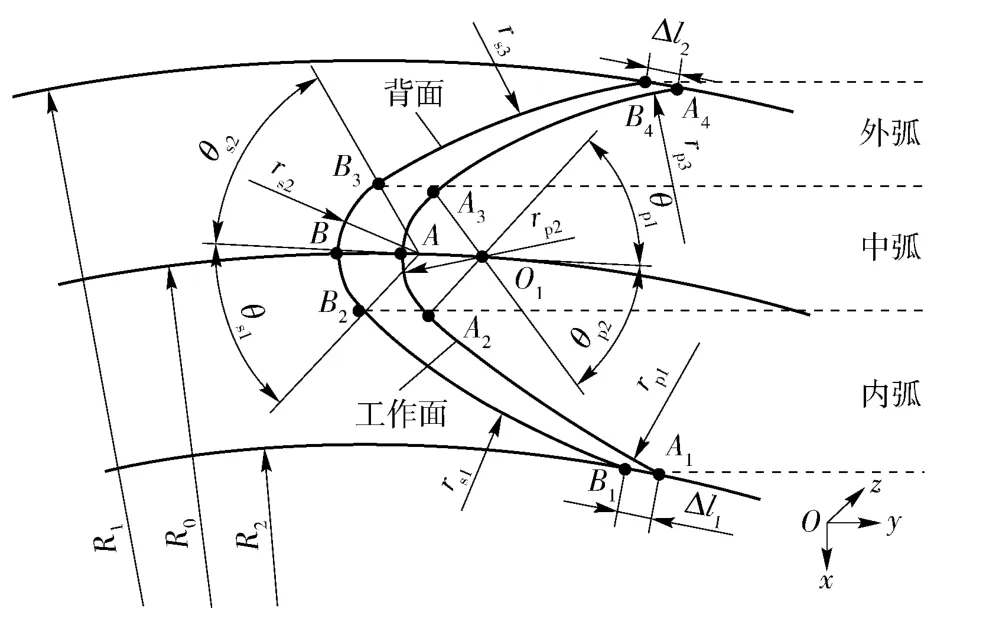
图2 叶片结构简图Fig.2 Schematic diagram of crescent-shaped blade

叶片工作面投影曲线由内弧A1A2，中弧A1AA3，外弧A3A4相切构成。中弧弧度为包角θp1与θp2之和，表征了工作面的弯曲程度。

工作面与循环圆内壁相交线离散点集为{Cn}，其中n=1，2，3.

式中:R 为循环圆半径;rp1、rp2、rp3分别为A1A2、A1AA3、A3A4半径，对应的圆心分别为Op1、O1、Op2.

在求解A2、A4坐标时，若rp1与rp3取值过小，容易产生空解，导致建模失败，故须增加约束条件。假设A1A2、A3A4分别与内环、外环仅存在唯一交点，此时rp1、rp3取到有效范围内的最小值rp1m、rp3m，记为

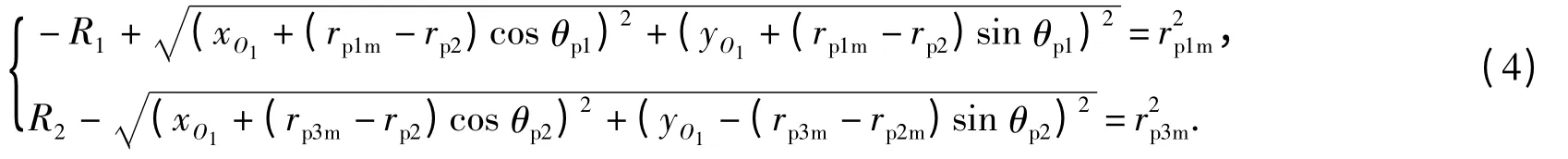
rpnm-θpn关系图如图3 所示。当设计参数取值rp1≥rp1m，rp3≥rp3m时，求解才具有意义。

可见，叶形参数间并不相互独立，rp1与θp1，rp3与θp2间存在几何约束关系。叶片背面受到工作面几何约束以及叶片入出口厚度限制，其参数可由工作面几何参数推导出。

综上提出弯叶片叶形设计参数:工作面内外弧半径(rp1、rp3)与叶形包角(θp1、θp2)，记为

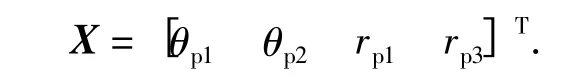
图4 为只改变θp1、θp2，而其余参数保持不变的周期流道参数化模型。

2 模型可信度分析

对于三维优化设计而言，其往往要进行成百次甚至上千次的仿真计算，单次计算耗时较长，且计算精度难以保证。为尽量降低计算时间，并保证计算精度，在优化计算之前，须对仿真模型的独立性与可信度进行检验［11］。

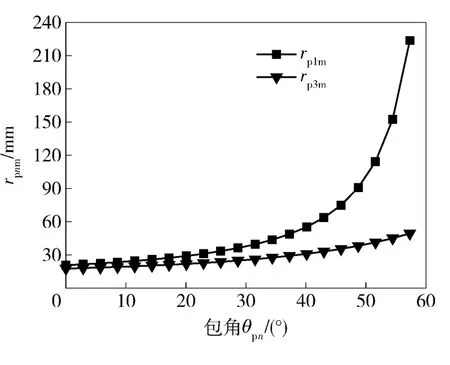
图3 rpnm-θpn关系图Fig.3 Relationship of rpnm and θpn

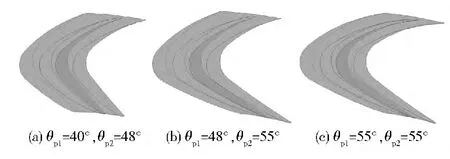
图4 单流道周期模型Fig.4 Model of periodic flows

针对某双循环圆液力缓速器样机，对其周期流道进行不同密度的非结构网格划分，统计网格数量m，并做自然对数处理lnm. 使用全隐式多网格耦合算法对计算模型进行粘性流动计算，湍流模型采用结合了自动壁面函数的切应力输运SST 湍流模型，并采用级联法确定动轮与定轮的数据交互性边界条件［12-14］。取动轮转速1 000 r/min 工况，进行网格数量相对于制动力矩T 与计算时间t 的独立性分析，并计算仿真误差η，如图5 所示。

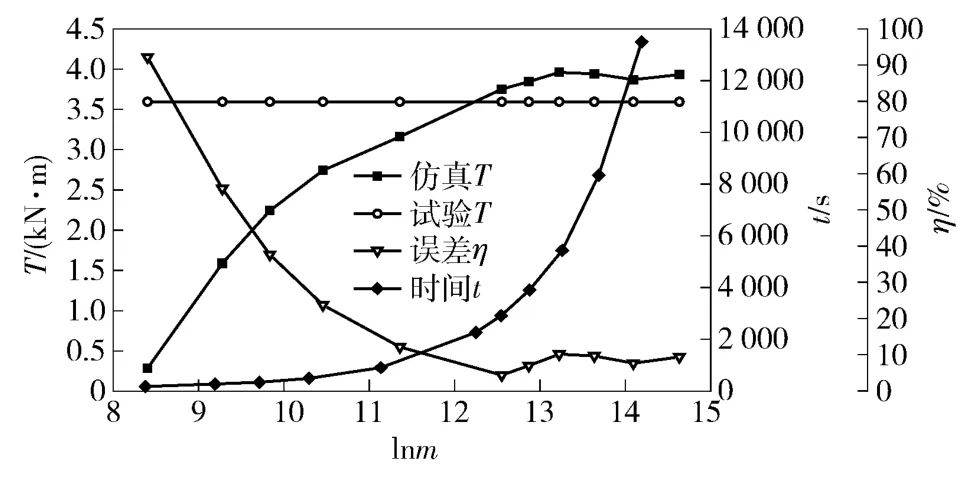
图5 网格独立性分析图Fig.5 Analysis chart of grid independence

由图5 可见，随着网格数量增加，仿真力矩逐渐上升，当网格数量达到一定程度后趋于收敛，同时计算时间随着网格数量增加呈指数型上升。综合考虑仿真的计算精度与成本，当网格自然对数取值12.55 时，全局网格尺度为1，网格总数为282 649，此时制动力矩计算结果趋于稳定，相对试验数据的误差仅为4.35%，计算时间也相对较短，在可接受范围内。基于网格独立性研究结果，对不同动轮转速n 下原样机计算结果与原样机试验结果进行对比，如图6 所示。

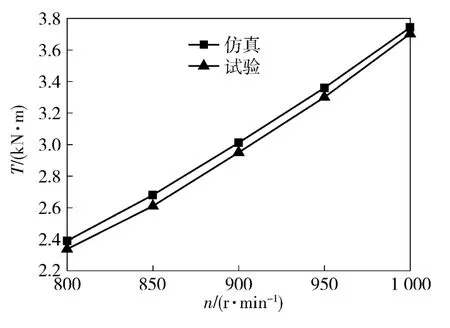
图6 仿真与试验制动力矩对比图Fig.6 Comparison of the simulation and experimental braking torques

由图6 可见，不同转速下原样机仿真结果与试验数据吻合均较好，平均相对误差在5%以内，证明了基于网格独立性验证的数值计算模型具有良好的可信度。

3 优化设计

将弯叶片叶形参数θp1、θp2、rp1、rp3作为设计变量，以提高制动力矩为优化目标，对叶形参数进行优化设计，设计流程如图7 所示。

为了缩短寻优过程，采用优化拉丁方设计方法进行试验设计(DOE)，基于试验结果构建响应曲面近似模型(RSM)，以制动力矩T 为单目标，利用多岛遗传算法(MIGA)在近似曲面上寻取最优解，并用三维流场计算方法对优化结果进行验算。

基于DOE 试验样本计算结果，就设计参数θp1、θp2、rp1、rp3对缓速制动性能敏感性进行分析。

图8 为取动轮转速1 000 r/min 时，θp1、θp2、rp1、rp3对制动力矩T 的主效应分析图。

由图8(a)和图8(b)可见，随着包角的增大，制动力矩均先增大后减小，且均在56°附近，制动力矩取得最大值。由图8(c)可以看出，当rp1＜400 mm时，制动力矩随rp1的增加明显增加，当400 mm ＜rp1＜1 000 mm 时，制动力矩基本保持不变，仅有微小的波动，而当rp1＞1 000 mm 时，制动力矩则随rp1的增加呈下降趋势。而图8(d)的制动力矩的变化趋势与图8(c)相反，随着rp3的增加，制动力矩减小，并在400 ～800 mm 区间保持稳定，而后力矩略有上扬，但变化梯度并不明显。

图7 优化设计流程图Fig.7 Flow chart of optimization design

为了获得较好拟合效果，提高寻优精度，采用四元四次回归方程来构造响应曲面，其构造方程为

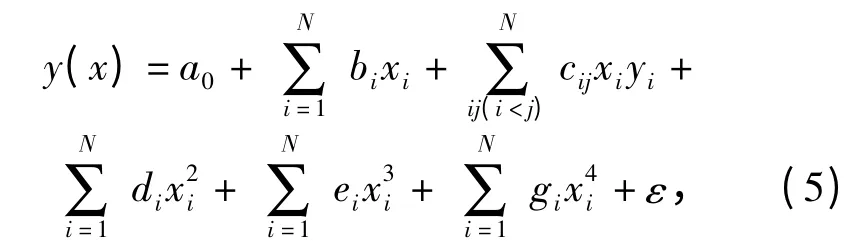
式中:y(x)为制动力矩T 响应系数;N=4，分别代表设计参数θp1、θp2、rp1、rp3;a0为常数项;bi为一次项系数;di为自变量二次效应系数;cij为各变量间交互效应系数;ei为三次项系数;gi为四次项系数;ε 为拟合误差。由参数敏感性分析结果可知，θp1、θp2、rp1、rp3对缓速器制动性能指标都有明显影响，故在此将4 个参数均考虑在内。

拟合度是用于表征拟合模型与实际数据吻合程度的量值，利用四元四次曲面构造的响应面的拟合度为0.934，大于许用值0.9，证明此响应曲面具有较高精度。

根据构造的响应曲面，建立制动力矩关于θp1与rp1，θp2与rp3的二维等值线图，如图9 所示。

由图9(a)可见，在以设计参数θp1为横坐标，rp1为纵坐标构造的等值线图中，目标值制动力矩存在一个明显的峰值。而以θp2为横坐标，rp3为纵坐标构造的等值线图中，如图9(b)所示，制动力矩在自变量范围内存在两个峰值，即当θp2处于58°附近，rp3取得较大值或较小值时都会出现制动力矩的极大值点。

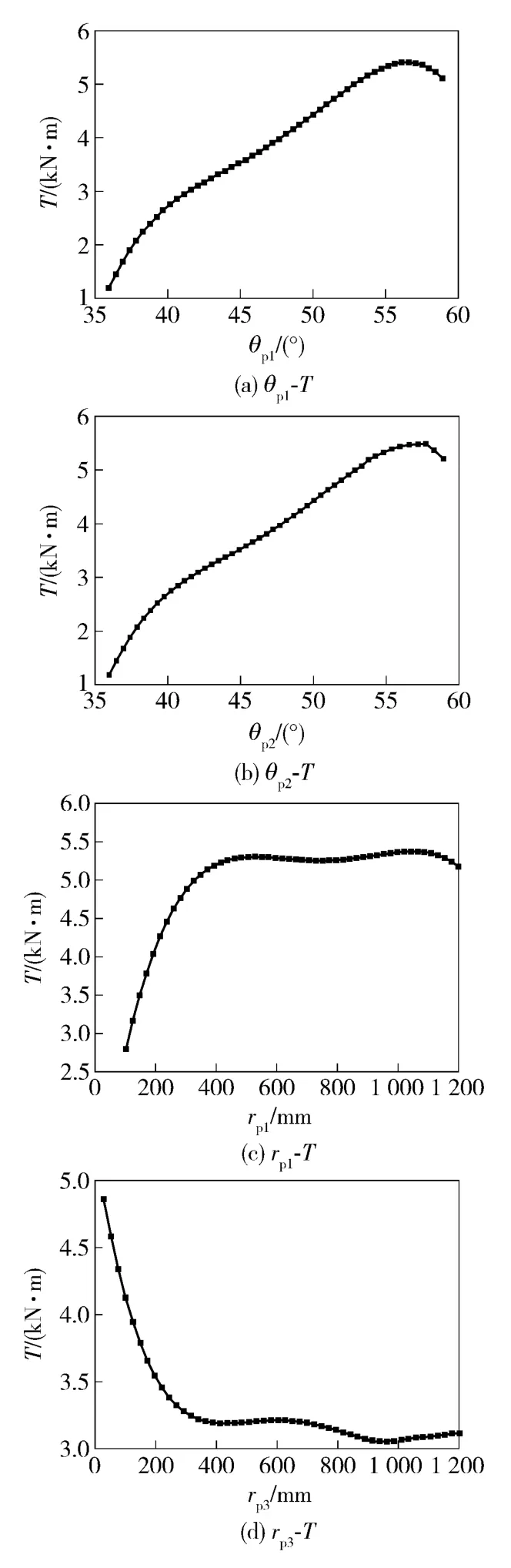
图8 主效应分析图Fig.8 Main effect diagram

在弯叶片叶形优化设计中，其目标函数具有多峰性与非连续性，设计参数间存在约束关系。MIGA作为一种伪并行遗传算法可以更好地解决此类优化问题［15］。在传统遗传算法基础上发展而来的MIGA，将整个进化群体划分为若干子群体，称为“岛屿”，在每个岛屿上对子群体独立地进行传统遗传算法的选择、交叉、变异等遗传操作，并定期随机选择一些个体进行迁移操作，借此可以维持群体的多样性，抑制早熟现象的发生。

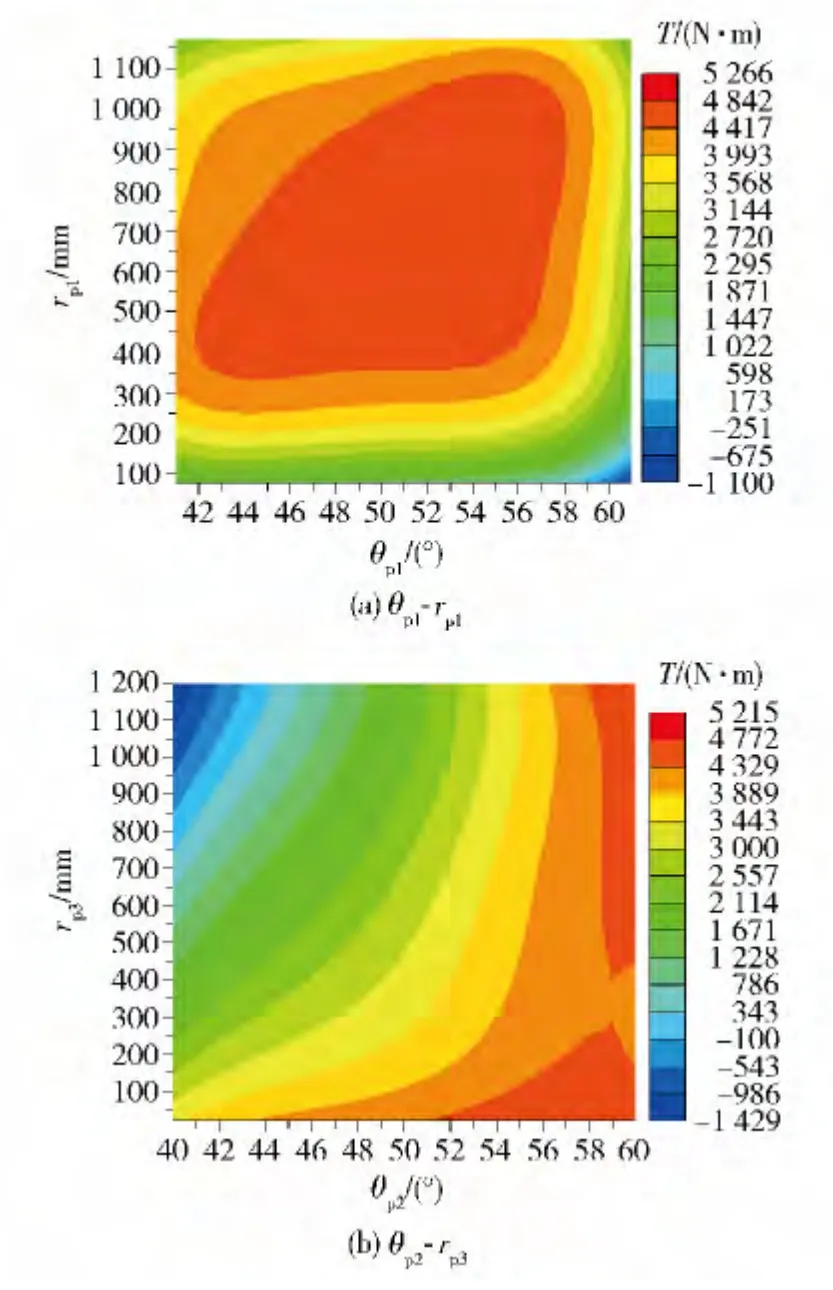
图9 等值线响应面图Fig.9 Contour diagram

采用MIGA 方法在RSM 曲面上进行寻优，通过3 000 步的迭代计算，得到最优解为

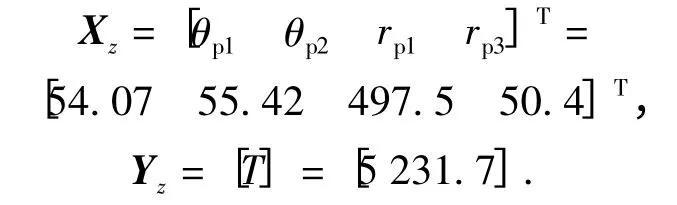
将最优解Xz代回原模型，进行三维数值验算后的制动力矩Ty=5 160 N·m. 由此可见基于RSM 与MIGA 优化方法获得的最优制动力矩较为精确，相对误差仅为1.39%.

原样机叶片叶形设计参数为

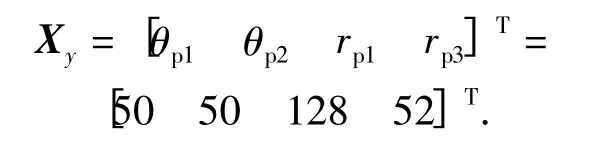
将原样机方案流场计算结果与最优解进行对比分析，图10 为原方案与最优方案定轮周期面速度矢量分布图。

从整体上看，两方案油液呈明显的循环流动，低速区均出现在循环圆中心B 处，高速区出现在循环圆外环靠近定轮入口A 处和出口C 处。而从原方案到最优方案，腔内流动速度明显增加，油液从动轮吸收了更多的能量，从而产生的冲击作用更为强烈，且循环流道从外到内的油液流速变化梯度亦增大，因此最优方案形成的涡旋区更为明显。

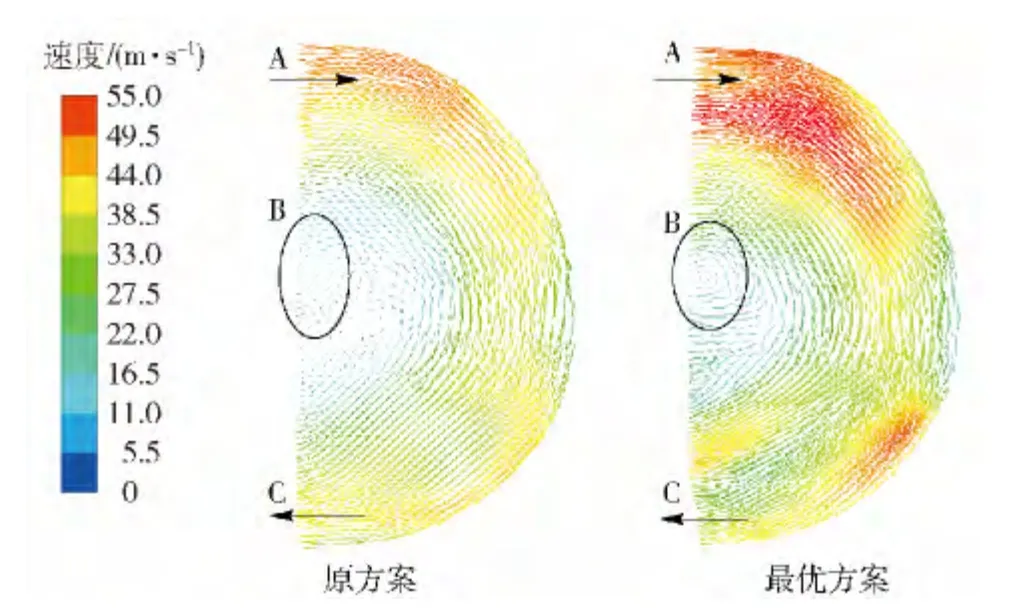
图10 速度矢量分布图Fig.10 Distribution of velocity vectors

液力缓速器作为将车辆机械能转换为油液热能的辅助装置，内腔湍流动能分布在一定程度上表征了内部流场涡旋强度与消耗能量的大小［16］。图11为原方案与最优方案定轮叶片背面中间流线处的湍流动能K 分布曲线。

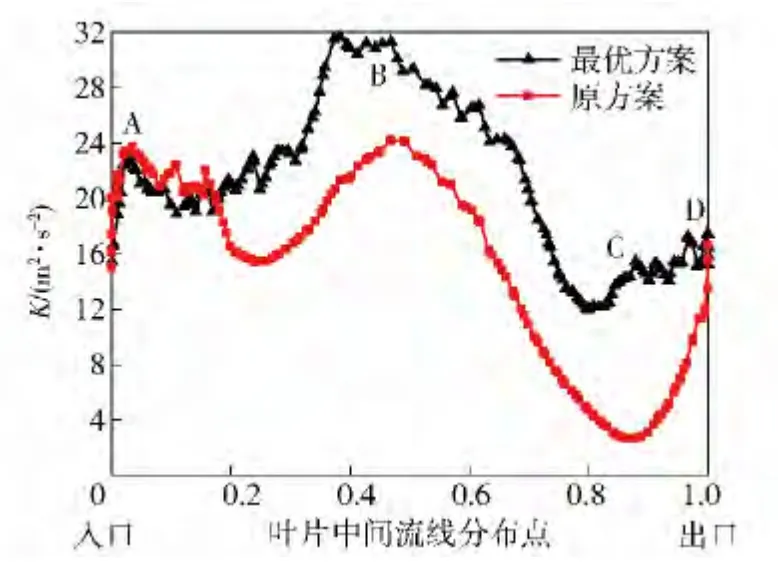
图11 湍流动能分布曲线Fig.11 Distribution curves of turbulent kinetic energy

由图11 可见，从叶片入口到出口，两方案中间流线上的湍流动能分布趋势基本一致。湍流动能极大区域均分布在叶片中部B 处，极小区域分布则在叶片下部C 处。流动的油液在叶片入出口A、D 处产生收缩与扩散损失，因而湍流动能较高，但由于入口处油液流速更高，所以A 处湍流动能分布值更大。

从原方案到最优方案，湍流动能分布值明显增大，这是由于油液整体流速增加，涡旋流动加剧，油液质点碰撞与混合所产生的湍应力增加，因而能量损失更大。

4 制动特性优化结果

将最优方案制动特性计算结果与原样机计算结果进行对比，如图12 所示。

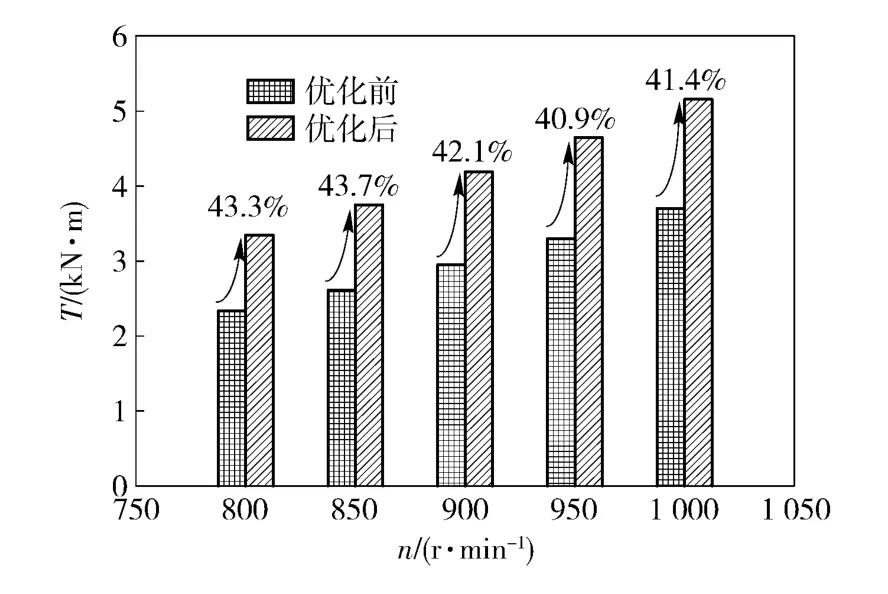
图12 优化前后制动特性对比图Fig.12 Comparison of brake performances before and after optimization

由图12 可见，最优方案制动力矩远高于原样机计算结果。在分析转速区间内，优化后制动力矩增幅均在40%以上，平均增幅高达42.3%. 由此可见，在缓速器循环圆尺寸保持不变的情况下，通过改变叶形设计参数θp1、θp2、rp1、rp3可以有效增加缓速器的制动性能，提高制动功率密度。

5 结论

1)结合优化拉丁方设计方法、响应曲面法及MIGA 对双循环圆液力缓速器叶形参数进行了优化设计。结果表明，优化方法适用于弯叶片优化，且具有较高的可信度。

2)设计参数θp1、θp2、rp1、rp3均对缓速器制动性能产生较大影响，优化后流场速度分布值与叶片湍动能分布值均增大，制动力矩平均提高了42.3%.

References)

［1］闫清东，邹波，魏巍，等. 液力减速器充液过程瞬态特性三维数值模拟［J］. 农业机械学报，2012，43(1):12 -17.YAN Qing-dong，ZOU Bo，WEI Wei，et al. Numerical investigation on transient oil-filling process of hydraulic retarder［J］. Transactions of the Chinese Society for Agricultural Machinery ，2012，43(1):12 -17. (in Chinese)

［2］Allison Transmission Inc. MD/HD/B series on-highway transmissions operator's manual［M］.Indiana:Allison Transmission Inc，2005.

［3］Allison Transmission Inc. 3000/4000 operator's manual［M］.Indiana:Allison Transmission Inc，2010.

［4］邹波. 车用液力减速器性能预测设计方法研究［D］. 北京:北京理工大学，2012.ZOU Bo. Research on brake performance prediction design method of vehicular hydraulic retarder［D］. Beijing:Beijing Institute of Technology，2012.(in Chinese)

［5］李雪松. 基于非稳态流场分析的车用液力缓速器参数优化方法研究［D］. 吉林:吉林大学，2010.LI Xue-song. Research on the parameter optimization method of automotive hydraulic retarder based on unsteady flow field analysis［D］.Jilin:Jilin University，2010. (in Chinese)

［6］李雪松，刘春宝，程秀生，等. 基于流场特性的液力缓速器叶栅角度优化设计［J］.农业机械学报，2014.45(6):20 -24.LI Xue-song，LIU Chun-bao，CHENG Xiu-sheng，et al. Cascade angle optimization of hydraulic retarder based on flow field characteristics［J］. Transactions of the Chinese Society for Agricultural Machinery，2014，45(6):20 -24.(in Chinese)

［7］邹波，陈日军，唐正华，等.液力减速器内流道数值建模方法研究［J］. 机床与液压，2011，39(9):100 -104.ZOU Bo，CHEN Ri-jun，TANG Zheng-hua，et al. Research on parametric modeling method of hydraulic retarder cascade［J］.Machine Tool ＆ Hydraulics，2011，39(9):100 -104.(in Chinese)

［8］闫清东，邹波，魏巍. 液力减速器叶片前倾角度三维集成优化［J］. 吉林大学学报:工学版. 2012，42(5):1135 -1139.YAN Qing-dong，ZOU Bo，WEI Wei. Research on 3-D integrated optimization of blade angles of hydraulic retarder［J］. Journal of Jilin University:Engineering and Technology Edition，2012，42(5):1135 -1139. (in Chinese)

［9］闫清东，邹波，唐正华，等.车用液力减速器叶片数三维集成优化［J］.农业机械学报，2012.43(2):21 -25.YAN Qing-dong，ZOU Bo，TANG Zheng-hua，et al. 3-D integrated optimization of blade angles of hydraulic retarder［J］. Transactions of the Chinese Society for Agricultural Machinery ，2012，43(2):21 -25. (in Chinese)

［10］王健，葛安林，雷雨龙，等. 基于三维流动理论的液力变矩器设计流程［J］. 吉林大学学报:工学版，2006，36(3):315-320.WANG Jian，GE An-lin，LEI Yu-long. Design flow of torque converter based on three dimensional flow theory［J］. Journal of Jilin University:Engineering and Technology Edition ，2006，36(3):315 -320. (in Chinese)

［11］Habashi W G，Fortin M，Vallet M G，et al. Anisotropic mesh adaptation:towards user-independent，mesh-independent and solver-independent CFD solutions. part Ⅰ:general principles［J］. International Journal for Numerical Methods in Fluids，2000，32(6):725 -744.

［12］Kim B S，Ha S B，Lim W S，et al. Performance estimation model of a torque converter. part I:correlation between the internal flow field and energy loss coefficient［J］. International Journal of Automotive Technology，2008，9(2):141 -148.

［13］Grigoriadis D G E，Bartzis J G，Goulas A. Efficient treatment of complex geometries for large eddy simulations of turbulentflows［J］. Computers and Fluids，2004，33(2):201 -222.

［14］Fuente P D l，Stoff H，Volgmann W，et al. Numerical analysis into the effects of the unsteady flow in an automotive hydrodynamic torque converter［C］∥Proceedings of the World Congress on Engineering. London，UK:IAENG，2011.

［15］Chen H，Ooka R，Kato S. Study on optimum design method for pleasant outdoor thermal environment using genetic algorithms and coupled simulation of convection，radiation and conduction［J］.Building and Environment，2008，43(1):18 -31.

［16］Lombargo F S，Lang P R. Atmospheric turbulence，meteorological modeling and aerody-namics［M］. NY，US:Nova Science Publishers，2010.