双电机耦合驱动履带车辆自适应滑模转向控制
2015-02-23盖江涛黄守道周广明刘翼马田
盖江涛,黄守道,周广明,刘翼,马田
(1.湖南大学 电气与信息工程学院,湖南 长沙410082;2.中国北方车辆研究所 车辆传动重点实验室,北京100072)
0 引言
采用电传动可以使履带车辆实现能源的多元化利用,比机械或液力机械综合传动具有诸多无可比拟的优点,如无级变速、效率高、易于布置、更适合于采用现代控制技术等优点[1]。转向控制技术极大地影响着车辆的机动性能。为了解决经典的双电机独立驱动无法实现履带车辆转向再生功率机械循环的问题[2],文献[3]提出了一种双电机耦合驱动技术方案,是典型的双输入双输出系统。
目前的电传动履带车辆转向控制策略,一般都没有考虑履带车辆的转向动力学过程对电机的驱动转矩做反馈性自适应调节,导致较难实现任意转向目标的跟踪控制。文献[4]基于神经网络PID 控制方法,实现了一定车速范围内的转向目标跟踪控制,但由于其神经网络主要针对电机阻力矩进行训练,较难体现履带车辆高速转向时的惯性力负载,只实现了低速转向具有较好的操控性能。文献[5]基于模型参考自适应控制方法,实现了差速转向控制,但控制效果较为依赖参考模型,稳定性较差。双电机耦合驱动虽然机械特性很好,但是双电机的耦合作用却使得转向控制更加复杂。如何针对履带车辆转向动力学固有特性来设计鲁棒性好的双电机耦合驱动控制算法,是履带车辆转向控制的难题。
本文在转向动力学模型存在不确定参量,以及两电机驱动转矩高度耦合的前提下,通过系统动力学解耦结合滑模变结构控制,建立了一种鲁棒性较好的转向控制算法,实现了对履带车辆转向的快速稳定控制。搭建了“驾驶员—控制器”在环的双电机驱动耦合履带车辆实时仿真系统,进行了不同工况的控制算法的仿真验证。
1 系统描述
1.1 履带车辆转向动力学模型
建立履带车辆转向动力学分析图(见图1),O 点在固定坐标系中的坐标(X,Y,Z)用于确定车辆中心的运动轨迹,C 点为固定坐标系的原点,θ 用于确定车体相对Y 轴的逆时针方向角,即车体绕Z 轴的转角,Z 轴方向与X、Y 轴由右手定则确定。x、y、θ作为随动坐标,它们的导数分别表示车辆纵向速度、车辆横向速度、转向角速度。
履带车辆的转向动力学模型为
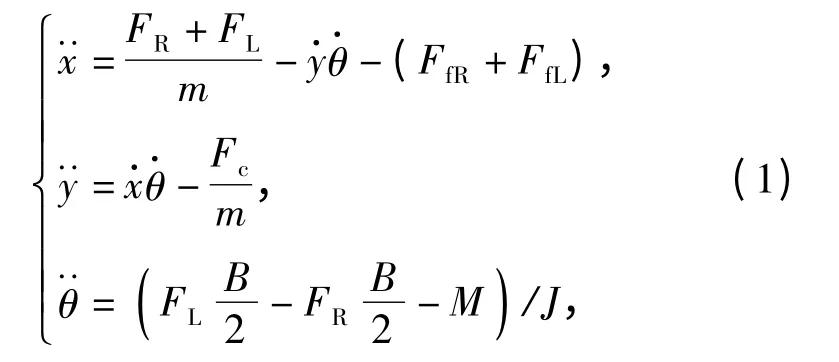
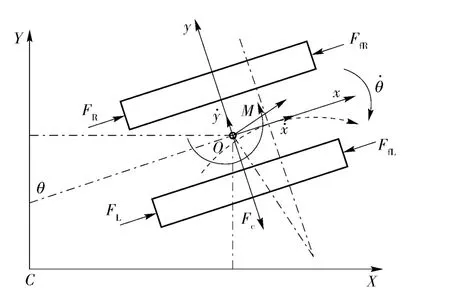
图1 履带车辆转向动力学分析图Fig.1 Steering dynamics of a tracked vehicle
式中:FL、FR分别为左、右侧的牵引力(力值为负时为制动力);FfL、FfR分别为左、右的行驶阻力;m 为履带车辆质量;g 为重力加速度;Fc为横向阻力;J 为车辆绕Oz 轴的转动惯量;B 为履带中心距;M为地面总转向阻力矩。
此外,还有以下关系式:
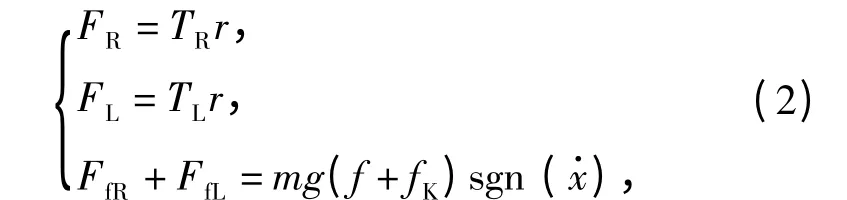
式中:TL、TR分别为左、右主动轮的阻力转矩;r 为主动轮半径;f 为地面行驶阻力系数;fK为迎风阻力和履带功率耗散的等效阻力系数。
履带车辆的运动是依靠履带推进的,履带的运动是由主动轮驱动的,主动轮出现转速差时,车辆就能产生相应的转向角速度。因此,主动轮才是实际的转向运动被控对象,建立两侧主动轮上微分方程:
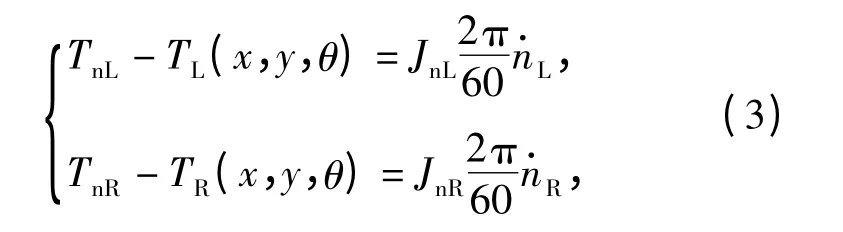
式中:TnL、TnR分别为传动系统传递至左、右主动轮的驱动转矩;nL、nR分别为左、右主动轮的转速;JnL,JnR分别为左、右主动轮的转动惯量。
1.2 双电机耦合驱动运动学和动力学关系
履带车辆双电机耦合驱动系统,由左右两侧驱动电机、耦合机构(中央3 个行星排)组成,如图2所示。电机带动耦合机构旋转,利用耦合机构差速差矩功能,调节两侧主动轮的驱动转矩以适应地面阻力,并在主动轮上形成速度差,实现车辆转向。其中:kL、kR、kO分别为左、右两侧普通排及中间双星复合排的特征参数,且kL=kR=k,kO=1;nmL、nmR分别为左、右电机的转速;TmL、TmR分别为左、右电机的输出转矩;ic为侧传动比。
根据行星传动运动学和动力学关系,在耦合机构作用下,可得如图2 所示的双电机耦合驱动系统的运动学、动力学关系:
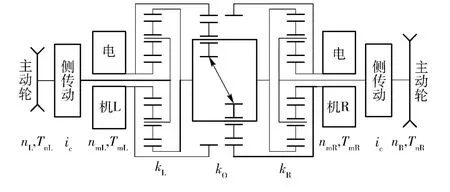
图2 双电机耦合电驱动系统图Fig.2 System structure of double motor coupling drive transmission
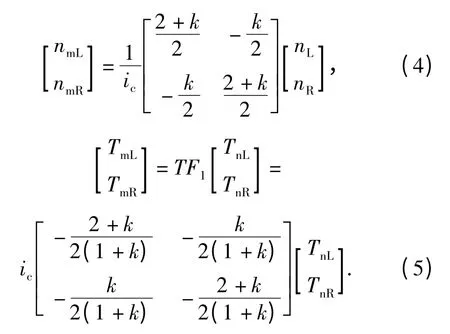
转向控制的目标就是通过控制两电机的转矩TmL、TmR,使左、右两侧主动轮转速nL、nR能跟踪其期望转速,从而驱动履带车辆实现预定的转向目标。
2 转向系统解耦及控制结构分析
履带车辆转向的控制是根据踏板、方向盘等驾驶操纵信号决定的期望车速v*、期望转向角速度ω*,以及反馈而来的主动轮转速nL、nR,解算出两电机的目标转矩指令经由前述分析,方程(1)式中x、y、θ 均较难观测,属于不确定的参数,不同工况下转向阻力矩难以实时预测,这就使得履带车辆转向系统具有多输入多输出(MIMO)、非线性耦合且参数不确定的特点。如图3 所示。
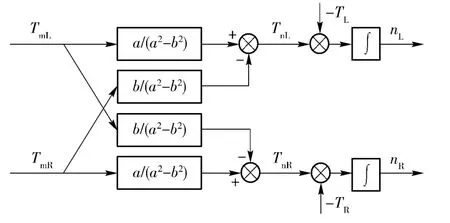
图3 原系统开环控制结构图Fig.3 Open loop control structure of the original system
为此,须进行系统解耦,以降低控制状态变量的耦合关联度。根据双电机耦合驱动履带车辆转向系统运动学关系,可通过以下状态变换设计系统解耦算法。
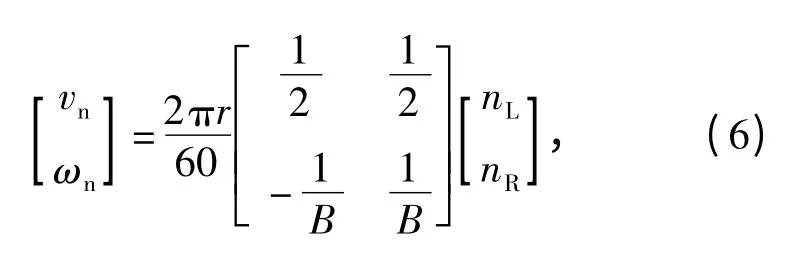
式中:vn即为经由主动轮转速变换得到的车速;ωn为相应的转向角速度。解耦同时,对系统其他参量做同步线性变换。
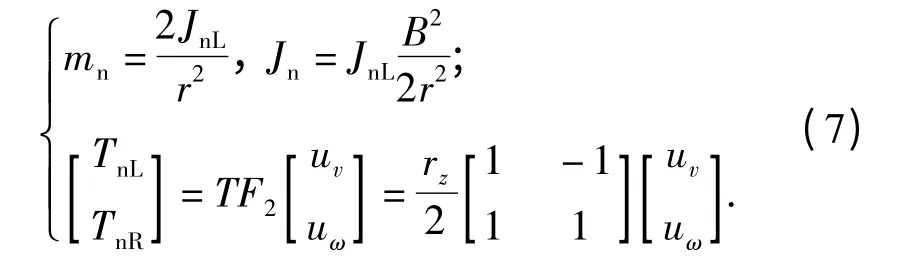
可将控制系统的动力学模型变换为
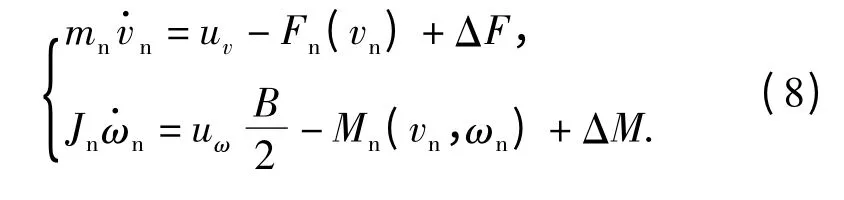
其中各项阻力为
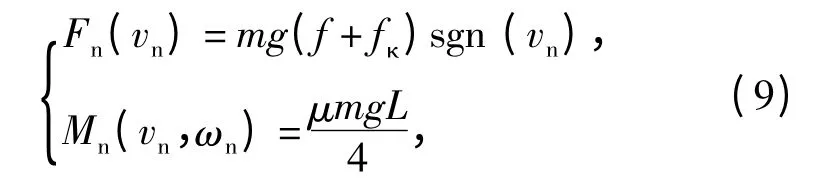
Fn、Mn则可由履带车辆转向行驶理论计算,其中μ是转向阻力系数,由尼基金计算模型[6]得到。
通过变换后的新系统的控制解耦拓扑结构如图4 所示。
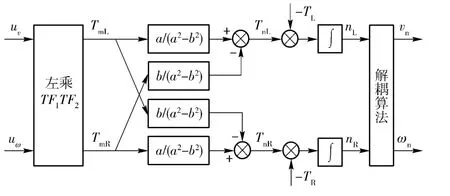
图4 新系统开环控制拓扑结构图Fig.4 Open loop control structure of the new system
解耦后的等效开环控制结构如图5 所示。
从解耦新系统的开环结构来看,状态变量之间的耦合作用大大减弱,原MIMO 系统近似变换为两个单输入单输出(SISO)的控制系统:一为车速控制系统;二为转向角速度控制系统。
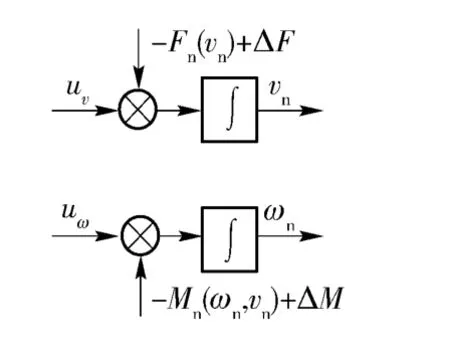
图5 解耦后的等效开环控制结构Fig.5 Equivalent open loop control structure of the decoupled system
解耦后的系统转向运动控制目标为:调节系统的等效转矩输入(uv、uω)T,使运动状态(vn、ωn)T跟踪期望的(v*、ω*)T。由(8)式可知状态vn将影响状态ωn的变化情况,而状态ωn不影响状态vn. 所以,将控制策略设计为:先针对v*完成vn的跟踪控制;随后将控制所得的vn视作已知参量,并针对ωn完成ω*的跟踪控制。
3 控制算法设计
由于状态vn将在一定程度上影响状态ωn的变化情况,而状态ωn不影响状态vn. 所以,控制时可以先稳定当前车速即保持主动轮转速和不变,再调节转向角速度即调节两侧主动轮转速差。这恰与履带车辆差速式转向的特点[7]相吻合。但新系统仍然具有一定的非线性和参数不确定性问题。滑模变结构控制方法,具有较强的鲁棒性控制特点,再加上综合设计的模糊及自适应算法,特别适合于解决前述系统的控制问题。
3.1 车速鲁棒滑模变结构控制算法设计
设计车速的鲁棒滑模控制算法为
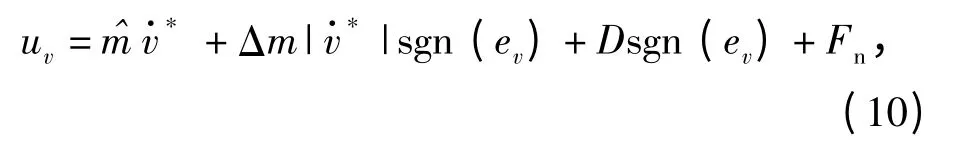
式中:
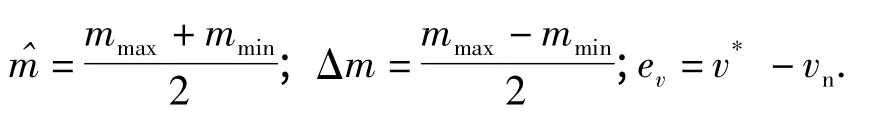
而mmax和mmin分别为惯量mn的上下界,可以预估或离线仿真确定。D 为满足下式的任意非零正数:

车速控制系统的Lyapunov 函数可取为

显然该函数是正定的。且有
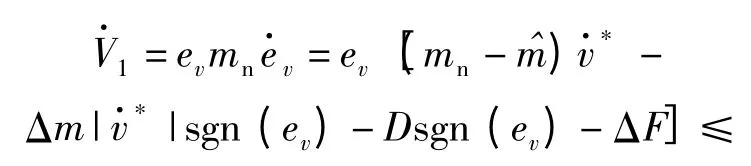

说明系统稳定,车速跟踪误差有界。
3.2 转向角速度自适应模糊滑模控制算法设计
解耦后得到的转向角速度控制系统中,Jn、Mn、ΔM 均未知,难以进行精确数学描述。三者虽然具有界限,但是在不同车速、转向角速度时其值波动较大,直接采用强制界限约束的经典滑模控制,极易产生较强抖振,系统控制不稳定。根据文献[8 -10],可将模糊逻辑系统及自适应控制方法引入到经典的滑模变结构控制当中。
定义转向角速度的跟踪误差为

定义积分滑模面
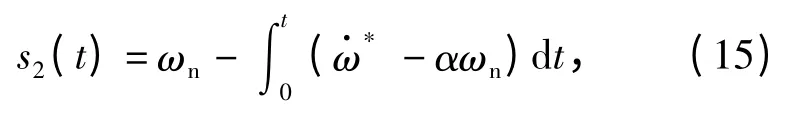
理想的最优控制算法应为
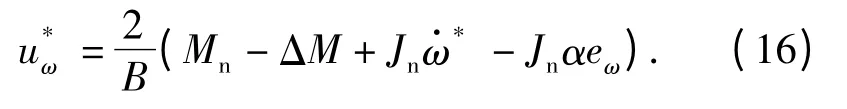
由于Mn和Jn未知,可设计模糊逻辑系统逼近
模糊输入设计为两个参量:s2,vn. 采用高斯型隶属函数,其一般形式为
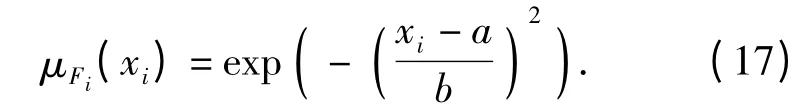
模糊规则的形式设计为
Rule:IF s2isvnisTHEN u is θl,其中:为模糊控制器输入量的模糊子集;θ =[θ1,θ2,…,θl]为模糊规则库中规则中的“则”部分对应的模糊集合的中心。输出量的反模糊化采用中心解模糊进行,为便于后文讨论,定义模糊集向量ξ=[ξ1,ξ2,…,ξm]T作为输出子集中心的权重,则有
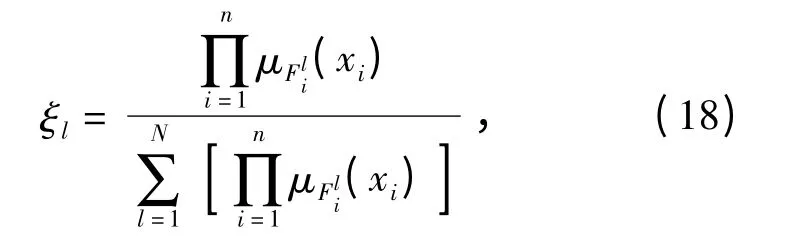
则该模糊逻辑系统所实现的模糊控制算法为
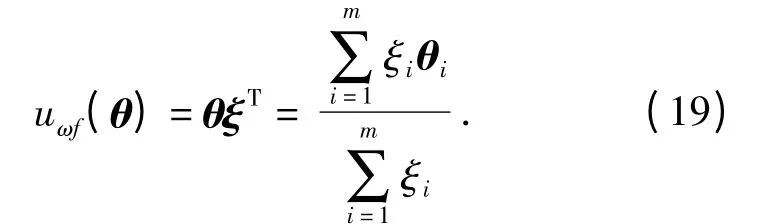
当取定可调参数为最优的θ*时,模糊算法的控制量uωf(θ*)将逼近,但仍然会有误差ε,有
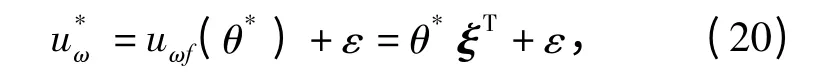
实际控制中,由于路面条件在变化,难以准确地找到θ*. 因此,采用其估计值即实际的模糊控制输出应当为
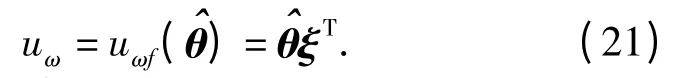
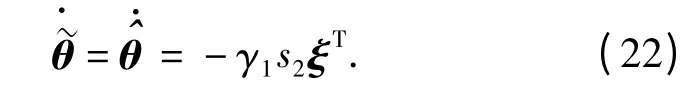
对于偏差ε,设计切换控制算法uωs来消除。
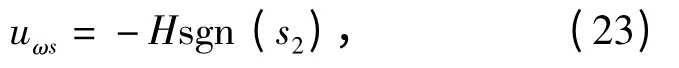
式中:H >εmax.
因此,转向角速度控制算法为
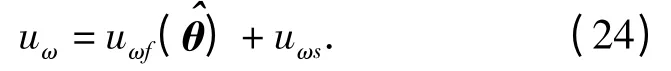
稳定性证明如下:
定义Lyapunov 函数
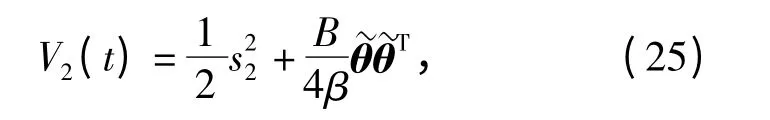
式中:β 为预定的正实数。
整理状态方程和滑动模态方程可知
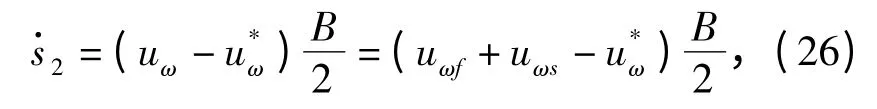
总有
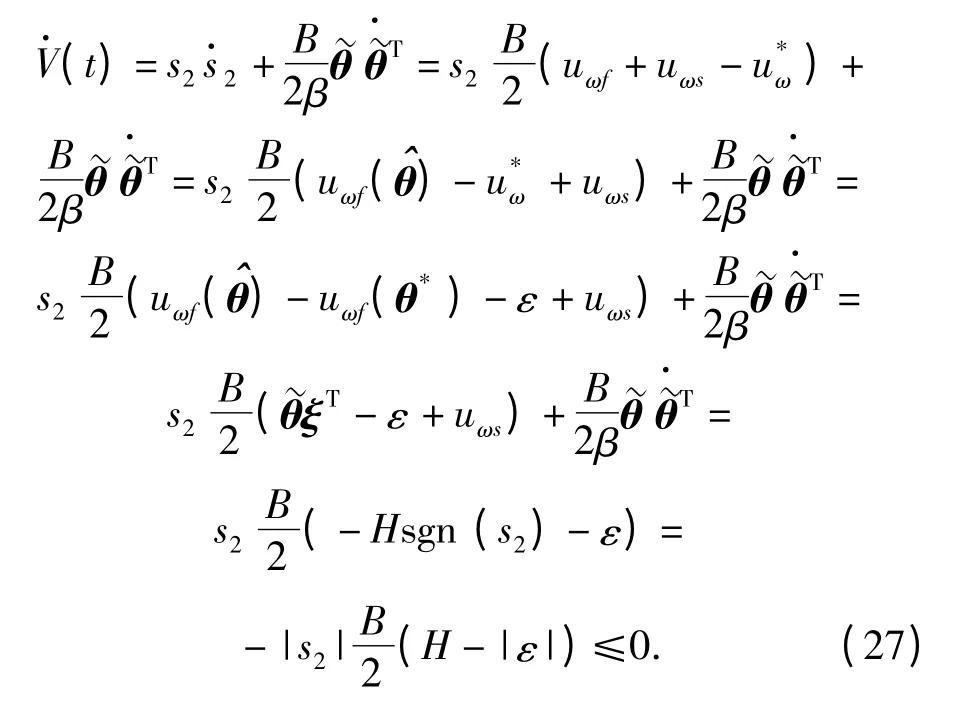
显然,系统是稳定的。
3.3 系统控制结构
综上所述,设计的双电机耦合驱动履带车辆控制结构如图6 所示。对于任意给定的期望车速v*、期望转向角速度ω*,都可以根据车速控制系统的鲁棒滑模控制算法求解出uv,根据转向角速度控制系统的自适应模糊滑模控制算法求解出uω,最终线性映射出电机的期望转矩指令控制电机完成合理的转矩输出,实现转向目标跟踪控制。
4 控制算法实时仿真与实验验证
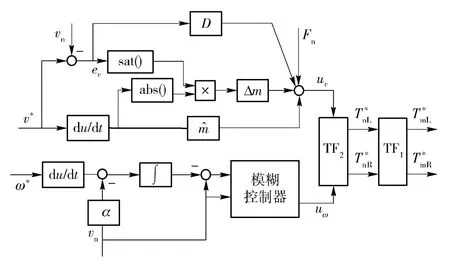
图6 双电机耦合驱动闭环转向控制结构Fig.6 Closed loop control structure of the double motor coupling drive transmission
为了验证控制算法的可行性和可实现性,通过搭建“驾驶员—控制器”[11]在环双电机耦合驱动履带车辆实时仿真系统(见图7),进行控制算法的实时验证。
操纵系统(方向盘、踏板)、综合控制器为实物;建立电机及其变频器、耦合机构等机械系统以及履带车辆等动态模型,运行在dSPACE 系统中DS4302进行实时模拟;控制算法通过代码自动生成,下载到综合控制器。通过操纵系统将驾驶员操作指令转换为输入信号输入综合控制器,综合控制器运行控制算法求得两个电机的目标转矩指令,通过CAN 总线发送给dSPACE 中运行的动态模型,进行控制算法的实时仿真验证。

图7 双电机耦合驱动履带车辆实时仿真系统Fig.7 Real time simulation system of the double motor coupling drive tracked vehicle
在柏油路(μmax取0.49,f 取0.038)路面下,通过油门踏板和方向盘配合,进行车辆转向实时仿真。
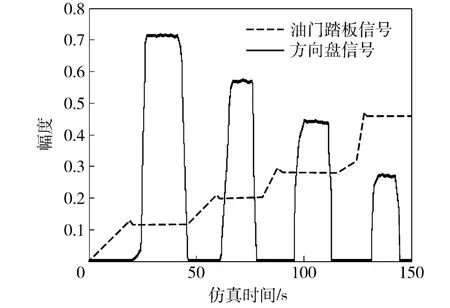
图8 踏板和方向盘信号Fig.8 Signals of accelerator pedal and steering wheel
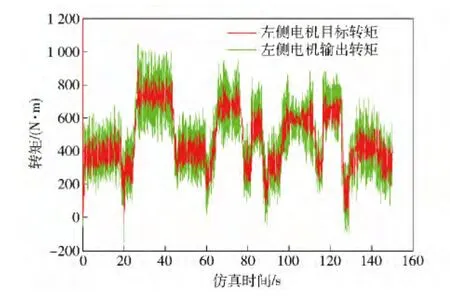
图9 左侧电机的目标转矩及输出转矩Fig.9 Target torque and output torque of left motor
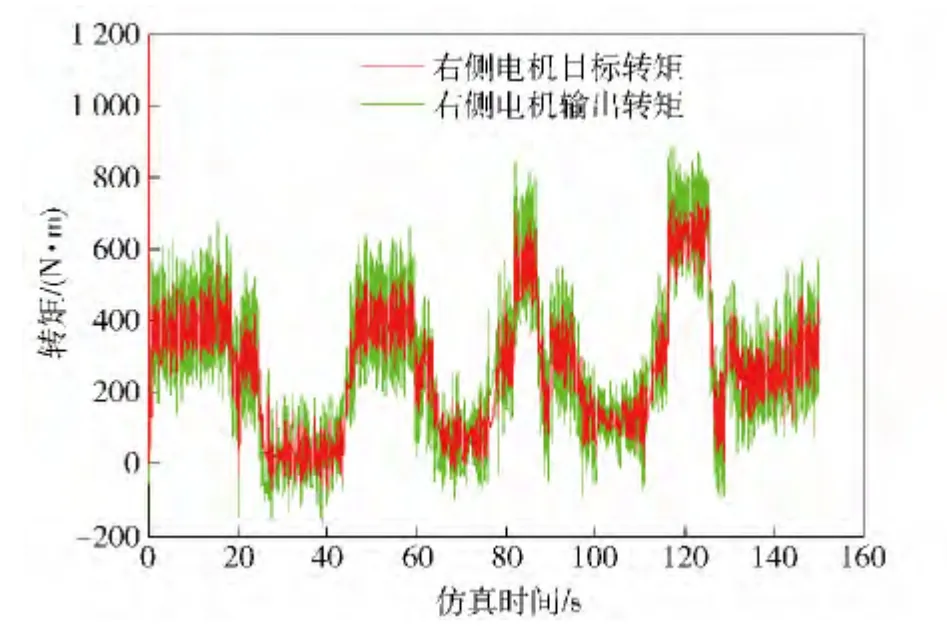
图10 右侧电机的目标转矩及输出转矩Fig.10 Target torque and output torque of right motor
仿真过程进行了4 次不同转速、转向角速度的转向实验,如图8 ~图12 所示。第1 次转向目标车速10.0 km/h,目标转向角速度0.32 rad/s 对应相对转向半径为3.0,实验时车速稳定在9.7 km/h,达到转向角速度0.31 rad/s,实现的相对转向半径为3.1;第2 次转向目标车速17.0 km/h,目标转向角速度0.37 rad/s 对应相对转向半径为4.5,实验时车速稳定在16.7 km/h,达到转向角速度0.35 rad/s,实现的相对转向半径为4.7;第3 次转向目标车速24.0 km/h,目标转向角速度0.30 rad/s 对应相对转向半径为8.0,实验时车速稳定在23.7 km/h,达到转向角速度0.29 rad/s,实现的相对转向半径为8.2;第4 次转向目标车速40.0 km/h,目标转向角速度0.19 rad/s 对应相对转向半径为21.0,实验时车速稳定在39.2 km/h,达到转向角速度0.19 rad/s,实现的相对转向半径为21.9.
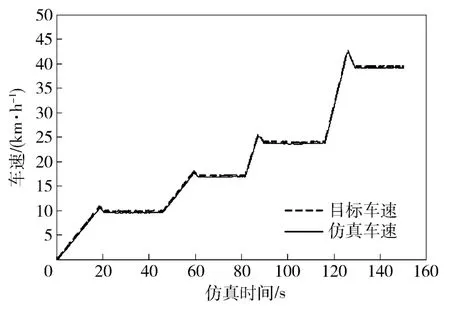
图11 目标车速及仿真车速Fig.11 Target and simulation forward speeds
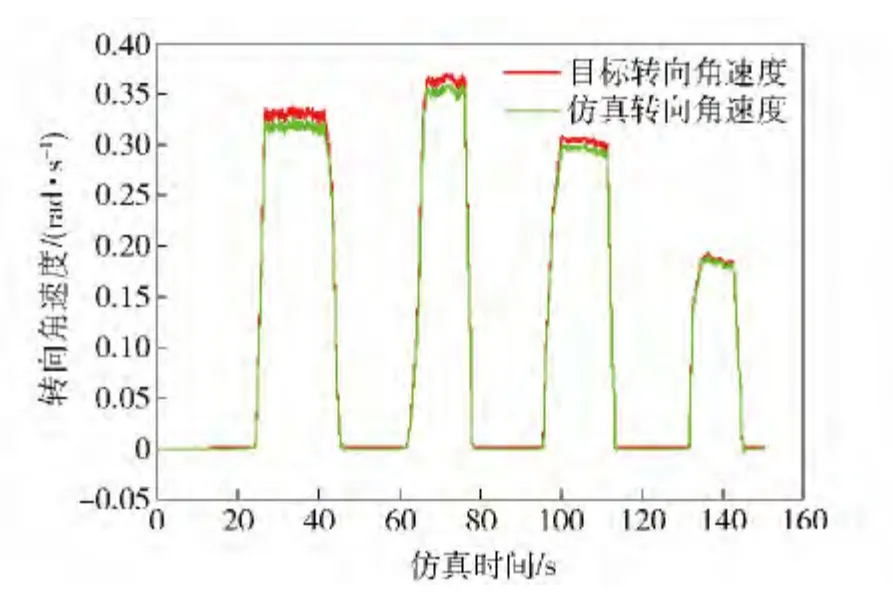
图12 目标转向角速度及仿真转向角速度Fig.12 Target and simulation steering angular speeds
通过仿真过程可以看出:1)应用“驾驶员—控制器”在环双电机驱动履带车辆实时仿真很好地验证了转向控制算法的可实现性;2)通过采用自适应滑模转向控制策略,解算左右电机转矩目标,实现了对车速控制目标、转向角速度控制目标的精确跟踪,具有很好的控制效果。
5 结论
1)提出了一种履带车辆双电机耦合驱动转向动力学的解耦算法,将原来的双输入双输出、非线性耦合系统解耦为两个SISO 系统,在不改变系统动力学特性的情况下,降低了参数之间的耦合作用,有利于控制律的设计。
2)基于解耦所得车速控制系统和转向角速度控制系统,分别设计了自适应模糊滑模控制算法,仿真结果证明其能实现车速和转向角速度的稳定控制。
3)在车速较高时,车速和转向角速度的控制误差比车速较低时要大,这是转向离心力增大的影响结果。因此,控制律还应针对此作进一步的改进。
References)
[1]史青录.电传动履带车辆转向动力学特性研究[D]. 北京:北京理工大学,2007:1.SHI Qing-lu. Study on dynamic characteristics of electric tracked vehicle on steering[D]. Beijing:Beijing Institute of Technology,2007:1. (in Chinese)
[2]孙逢春,张承宁. 装甲车辆混合动力电传动技术[M].北京:国防工业出版社,2008.SUN Feng-chun,ZHANG Cheng-ning. Technologies for the hybrid electric drive system of armored vehicle[M].Beijing:National Defense Industry Press,2008. (in Chinese)
[3]盖江涛,李慎龙,周广明,等. 一种履带车辆机电复合传动装置:中国,CN101985279A[P].2011-11-02.GAI Jiang-tao,LI Shen-long,ZHOU Guang-ming,et al. A type of electro-mechanical transmission for tracked vehicle:China,CN101985279A[P].2011-11-02. (in Chinese)
[4]翟丽,孙逢春,谷中丽.电子差速履带车辆转向转矩神经网络PID 控制[J].农业机械学报,2009,40(2):1 -4.ZHAI Li,SUN Feng-chun,GU Zhong-li. Neural networks PID control of steering torque for electronic differential tracked vehicle[J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(2):1 -4. (in Chinese)
[5]刘翼,毛明,马晓枫,等.零差速电传动履带车辆转向负载自适应控制策略研究[J].车辆与动力技术,2013(1):7 -11.LIU Yi,MAO Ming,MA Xiao-feng,et al. Research on self-adaptive steering control strategy for single motor cross drive electric transmission for tracked vehicles[J]. Vehicle & Power Technology,2013(1):7 -11. (in Chinese)
[6]LIU Long,ZHAI Li,FENG Hui-xia. Effects of dynamic characteristics of motor on steering dynamics of electric drive tracked vehicle[J].Journal of Beijing Institute of Technology:English Edition,2011,20(2):149 -156.
[7]Wong J Y,Chiang C F. A general theory for skid steering of tracked vehicles on firm ground[J]. Proceedings of the Institution of Mechanical Engineers,2001,215(3):343 -355.
[8]刘金琨. 滑模变结构控制MATLAB 仿真[M]. 北京:清华大学出版社,2005,379 -387.LIU Jin-kun. Sliding mode control design and MATLAB simulation[M]. Beijing:Tsinghua University Press,2005:379 -387. (in Chinese)
[9]王声远,霍伟.不确定非完整动力学系统的自适应模糊滑模控制器[J].控制理论与应用,2003,20(3):427 -431.WANG Sheng-yuan,HUO Wei. Adaptive fuzzy sliding-mode controllers of uncertain dynamic nonholonomic systems[J]. Control Theory & Applications,2003,20(3):427 -431. (in Chinese)
[10]刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407 -418.LIU Jin-kun,SUN Fu-chun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory &Applications,2007,24(3):407 -418. (in Chinese)
[11]邹渊,孙逢春,张承宁.电传动履带车辆“驾驶员——综合控制器”在环的双侧驱动控制实时仿真[J]机械工程学报,2007,43(3):193 -198.ZOU Yuan,SUN Feng-chun,ZHANG Cheng-ning. Electric tracked vehicle real-time simulation of dual-motor driving control with driver-global controller in-loop[J]. Chinese Journal of Mechanical Engineering,2007,43(3):193 -198. (in Chinese)
