基于截断总体最小二乘算法的车载三轴磁力仪标定

张滢，杨任农，李明阳，左家亮，陈星伊

(1.空军工程大学 航空航天工程学院，陕西 西安710051;2.西安卫星测控中心，陕西 西安710043)

0 引言

三轴磁力仪是一种低成本的导航定向传感器［1］。它通常与其他传感器组合以获得捷联载体的航向估计［2-3］。以陆用车辆导航为例，捷联三轴磁力仪通过测量地磁场矢量在体坐标系的投影，然后借助其他姿态传感器如惯性测量单元(IMU)提供的倾角信息将之转换到当地水平坐标系下，计算出车体与磁北方向的夹角，最后利用当地磁偏角对其进行修正以得到车辆与地理北的夹角，即航向角。但是，磁力仪的输出经常受到干扰磁场的影响。这些磁场会严重降低航向估计的精度。因此，在使用磁力仪之前，需要对其进行标定。

目前，已经有许多方法相继被提出用于解决三轴磁力仪的标定问题。文献［4 -5］提出两步法并给出了闭合解。该方法通过定义中间变量，将磁力仪的非线性观测方程转换为线性方程形式AX =b，其中系统矩阵A 和数据矩阵b 都由磁力仪测量数据构成，而X 是未知的中间变量。方程的解可以采用标准的线性最小二乘方法进行估计。文献［3，6 -8］采用椭球拟合的思想对磁力仪进行标定，其算法核心是采用最小二乘或自适应最小二乘方法。文献［9］针对磁力仪的观测方程等式两边同时含有噪声的情况，提出了基于总体最小二乘(TLS)算法的磁力仪标定方法。

注意到现有的磁力仪标定方法要求传感器能够在不同方向上进行旋转以获得尽可能多的方向的测量值。但是在车载磁导航应用中，车体受到路面的约束而不能实现空间全方向的转动，与之固连的磁力仪将难以获取全方向的磁场信息。因此，上述用于标定磁力仪标定的线性观测方程将面临病态问题。如果没有对应的方法对病态问题进行适当地处理，那么传统的标定方法将产生不可靠的解，甚至无解。为了获得鲁棒的解，通常需要引入正则化方法。传统的正则化方法如Tikhonov 正则化［10］假设线性观测方程的右边部分受到噪声干扰，而左边部分则是精确的。但是在磁力仪标定问题中，系统矩阵A和数据矢量b 都同时被测量噪声所干扰。因此，在选择正则化方法时，选择一种能够同时处理等式两边误差的方法更为合适。本文采用截断总体最小二乘(TTLS)方法对车载磁力仪进行标定。TTLS 方法适合处理强病态情况下的线性最小二乘求解问题［11］。车载磁导航实验结果表明，TTLS 方法能够有效地抑制磁力仪标定中的病态问题，获得良好的标定效果。

1 磁导航原理

车载磁导航系统主要由三轴磁力仪和IMU 组成。由于车体并不总是在水平面上行驶，使得磁力仪很难保持水平状态，为此在解算航向角时需要进行倾角补偿。倾角信息主要由IMU 经过惯性解算实时提供。由于磁力仪与车体捷联，其输出值为地磁场在体坐标系下的投影。为了确定航向角，这些投影值需要转换到当地水平坐标系下，其转换公式［1］为

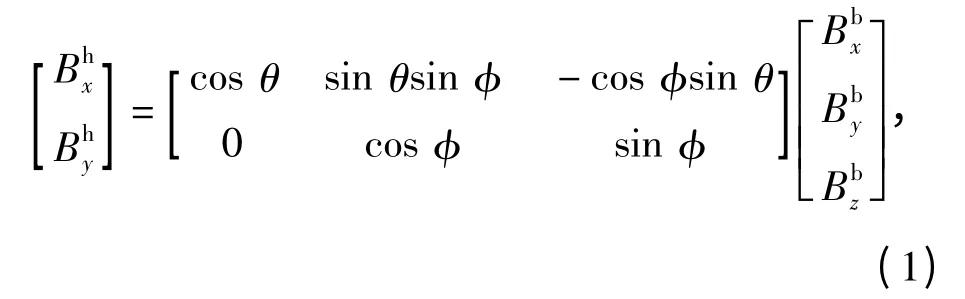
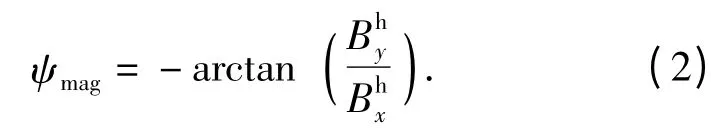
对ψmag进行当地磁偏角δ 的修正，即可得到车体与地理北之间的夹角，此即为航向角。δ 值可通过查询全球磁场模型得到［12］。

2 传感器误差模型

地磁场的测量误差来源于传感器自身的误差(非正交误差、刻度因子误差和零偏误差)和载体磁场干扰(硬磁误差和软磁误差)。在数学上，这两类误差统一建模为总非正交误差、总刻度因子误差和总零偏误差［3-4，8，13-14］。磁力仪的输入输出过程［4］可描述为

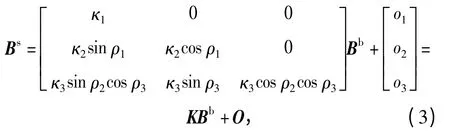
式中:Bs是地磁场矢量在传感器坐标系下的投影;Bb是地磁场矢量在体坐标系下的投影;ρ1、ρ2、ρ3是总非正交误差角;κ1、κ2、κ3是总刻度因子误差;o1、o2、o3是总零偏误差。

如文献［4］所示，总非正交误差角来源于磁力仪的制造工艺误差、磁力仪安装误差以及软磁误差;总刻度因子误差则来源于传感器刻度因子误差和软磁误差;总零偏误差由传感器零偏误差和硬磁误差组成。三轴磁力仪的标定模型可对(3)式进行逆向映射得到，即

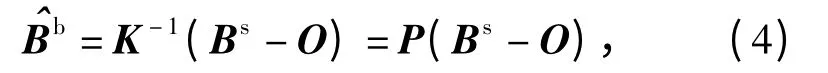
假设捷联三轴磁力仪在一个固定磁场的区域旋转，那么磁力仪标定后的输出将约束分布在以当地地磁场幅值为半径的圆球表面上，即有

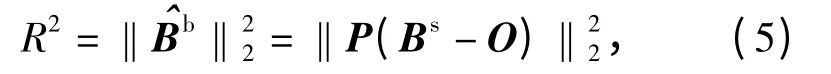
式中:R 是当地地磁参考场的幅值。将(4)式和(5)式展开可得

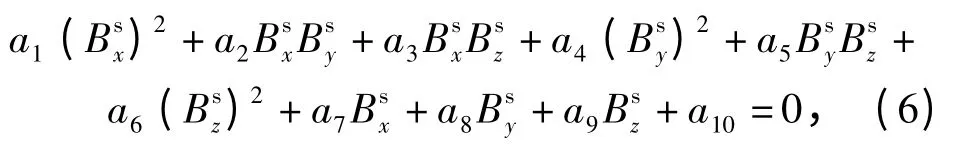
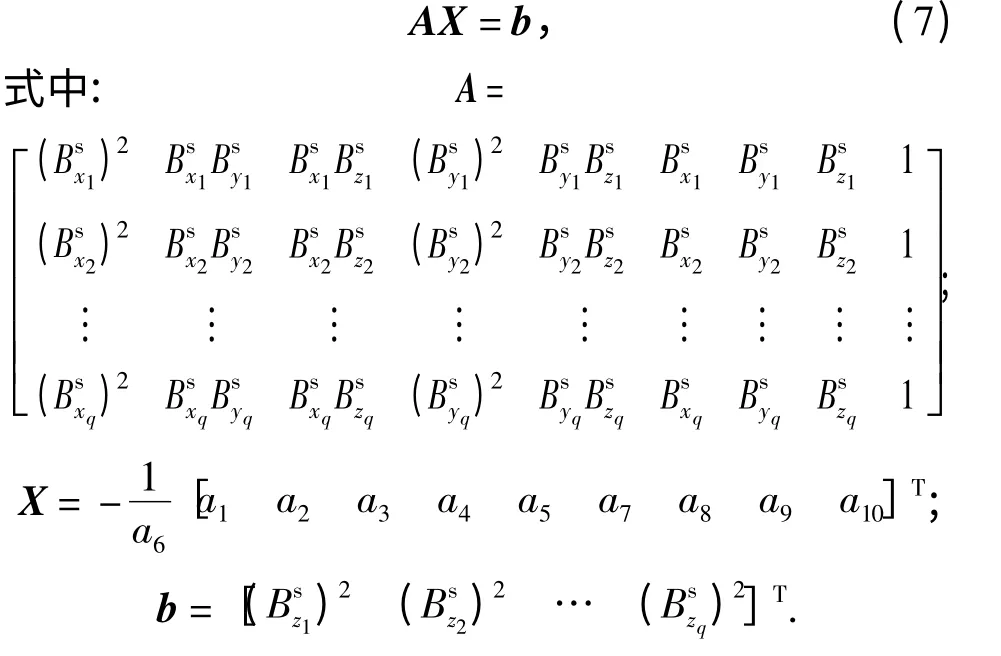
注意到数据矢量b 的构成可以从观测方程中任意选取。地磁场测量个数q 远大于观测方程中的未知量个数，因此(7)式是一个超定线性方程组。一旦方程组求解出未知量，即可从中解算出标定参数的估计值和

3 总体最小二乘标定方法

在磁力仪标定中，系统矩阵A 和数据矩阵b 都受到测量噪声的干扰，导致(7)式可能是不相容的。在此情况下，线性最小二乘解不再是最优的。文献［9］采用TLS 算法来处理系统矩阵A 和数据矩阵b 都存在误差的情况。TLS 通过最小化以下指标得到问题的解:

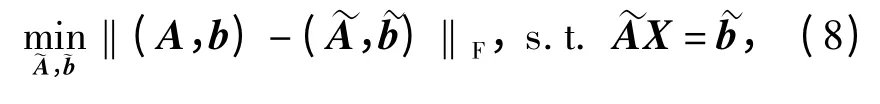
式中:‖＊‖F是Frobenius 模和分别是包含误差量的A 和b. (8)式的求解可以参考文献［15］。首先，对扩展矩阵(A，b)进行奇异值分解，得

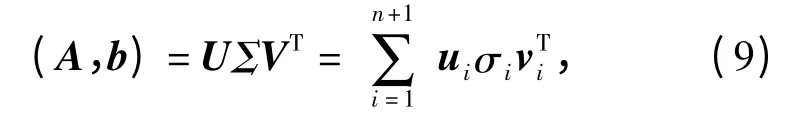
式中:n 是X 的维数;σi是第i 个奇异值，并且有σ1≥σ2≥…≥σn+1;ui是矩阵U 的第i 列矢量，U∈ℝm×m，UTU = Im;vi是矩阵V 的第i 列矢量，V∈ℝ(n+1)×(n+1)，VTV = In+1;Σ = diag(σ1，…，σn+1)。如果矩阵A 是满列秩的，那么(8)式可得到闭合解［16］为

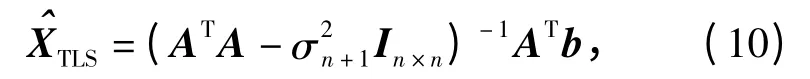
式中:σn+1是扩展矩阵(A，b)的最小奇异值。从统计的角度看，σ2n+1In×n是误差协方差的估计矩阵。与最小二乘方法相比，TLS 方法从协方差矩阵ATA中移去测量误差使之能够获得更高精度的解，其付出的代价是TLS 的解过程，是降正则化的。

4 截断总体最小二乘标定方法

在车载磁力仪标定中，车体的机动受到限制。车体一般绕天向轴进行顺时针或逆时针的旋转获得用于标定磁力仪的地磁测量数据。当车体在水平面内时，由于垂直方向上的地磁测量误差无法被充分激励，这些测量数据只能满足二维磁力仪(两个正交敏感轴固定在水平面内)的标定，无法满足三维轴磁力仪的标定［6］。由这些测量数据组成的磁观测方程，将会导致系统矩阵A 的条件数很大，即观测方程是病态的。如果不针对该问题进行适当地处理，那么车载磁力仪标定问题将可能得到不可靠的解，甚至是无解。为了求得稳定的解，需要引入正则化方法。

在选择正则化方法的时候，所选算法应具备处理等式两边的误差能力。TTLS 方法是基于TLS 方法发展而来的，它适用于严重病态的、方程等式两边都存在误差的线性求解问题。该方法的基本思想是通过截断小的奇异值对应的解的部分，使得解更为稳定，其算法流程总结［11］如下:

1)计算(A，b)的奇异值分解;

2)选择适当的正则化参数k(k≤n);

3)对矩阵V 进行分块，

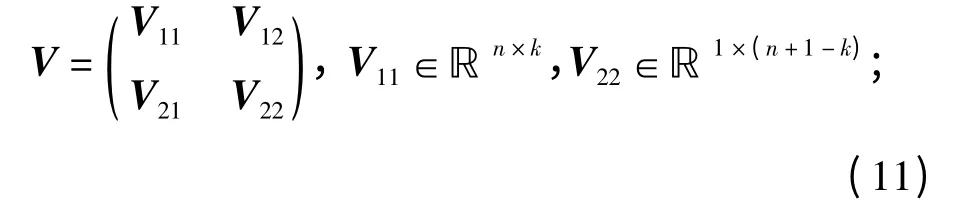
4)TTLS 的解可通过下式得到:

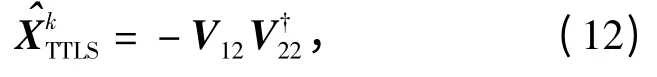
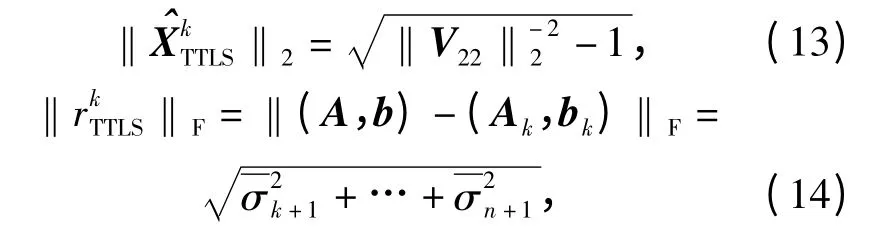
式中:(Ak，bk)是(A，b)的秩k 最佳逼近;到是(A，b)的对应的奇异值;代表对解的平滑度约束;代表对数据的拟合度。随着参数k 的增加，相继增加相继减小。为此k 的取值应该是上述两个模值平衡的结果。近些年，许多选择正则化参数的方法相继被提出，但是每一种方法都不能够适用于所有的病态问题，因为正则化参数的最佳选择是依据所解决的问题而定的。

本文选择L 曲线法［18］作为正则化参数确定的方法。L 曲线准则是以为横坐标，以为纵坐标，可得到许多点，这些点通过拟合得到一条形状如字母“L”的曲线。曲线的拐点能够较好地平衡上述两方面的信息并且同时保持它们的取值较小。因此，拐点所对应的正则化参数即为L 曲线法的最优值。

5 实验与结果

为验证TTLS 标定方法的有效性，将车载磁导航系统安装在面包车体内进行测试。为准确估计磁导航的精度，车体内部独立安装了惯性导航系统/全球定位系统(INS/GPS)组合导航系统，可提供最大精度误差为0.1°的航向角作为参考。

选择一块地磁场恒定的区域作为标定区，测得真实磁场值作为参考;然后让车在该区域内旋转，旋转过程中尽量地改变俯仰角。车载三轴磁力仪测得旋转过程中的地磁场数据，用于对磁力仪的标定。通过计算可知系统矩阵A 的条件数为1.36 ×1010，表明该线性观测方程是严重病态的［19］。TLS 标定方法由文献［9］提出，其标定效果要好于椭球拟合法，因此本文采用TLS 法与TTLS 法进行对比。利用TLS 和TTLS 标定算法处理测量数据，可得到磁力仪的标定参数如表1 所示。

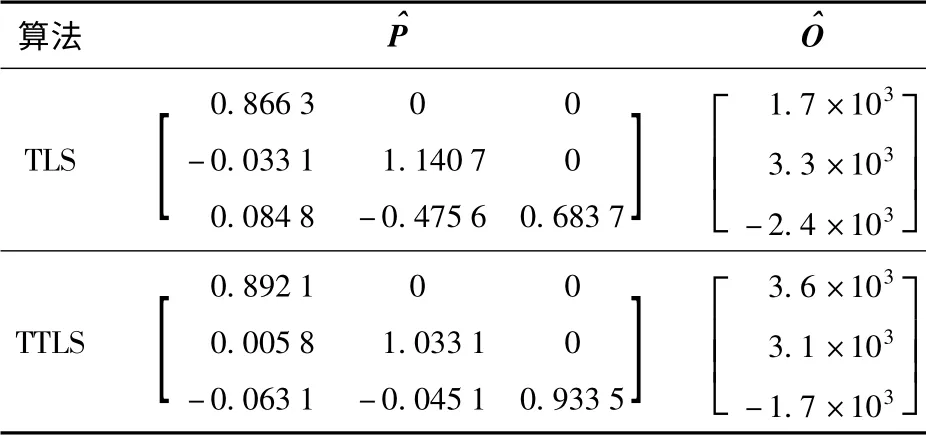
表1 参数估计结果Tab.1 Parameter estimates

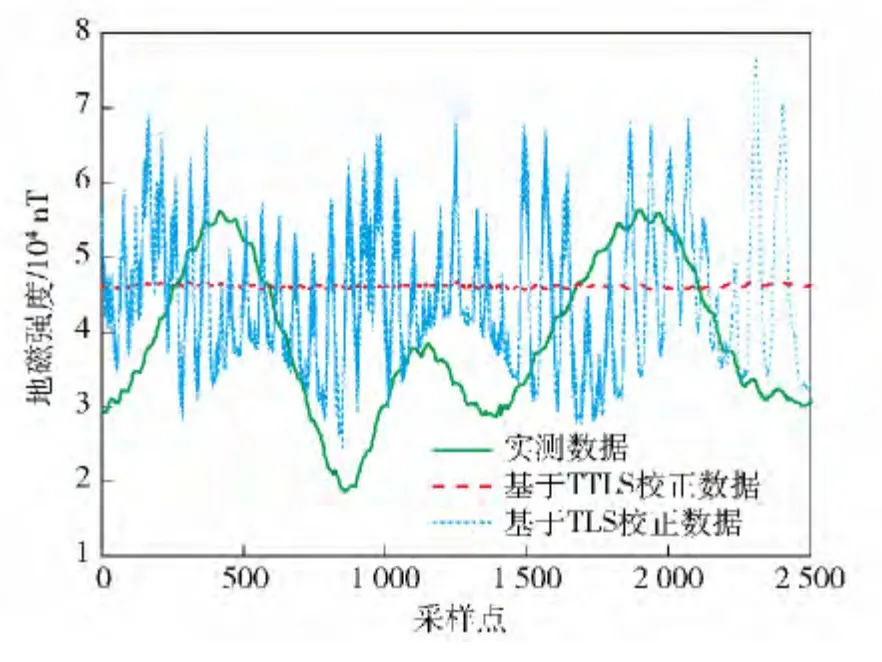
图1 TLS 和TTLS 标定结果对比Fig.1 TLS versus TTLS calibrated total magnetic field

图1是TLS 和TTLS 标定结果对比。图中实线为车载三轴磁力仪测得的实时数据，由于仪器以及载体干扰磁场的影响，未标定的地磁曲线偏离真实磁场值(46 100 nT)较大，其峰峰值差异约20 000 nT. 点线为TLS 法的标定结果，因为系统病态，由TLS 标定后的测量曲线已经远远偏离了真实值，并没有起到标定的效果，这表明TLS 法无法应用于病态情况下的三轴磁力仪标定。虚线为TTLS 方法标定结果，其标定后的测量值则接近地磁场值。令表示标定后的地磁场测量值，r0表示真实磁场值，那么标定后的相对均方根误差rmse 可由下式计算得到:

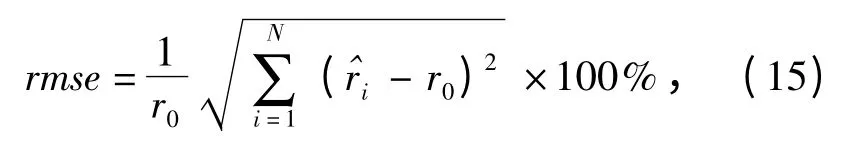
式中:N 表示地磁场测量个数。经计算可知由TTLS标定后的磁场值均方根误差小于1%. 实验结果表明TTLS 标定方法能够准确地估计磁场误差并进行有效地补偿，表明正则化技术是标定方法在病态问题中获得鲁棒解的关键性因素。

由于TLS 方法无法应用于病态条件下的三轴磁力仪校正，也无法进行航向角的估计，因此在航向角比较实验中，本文采用椭圆拟合法［20］与TTLS 标定法来比较结果。图2 是磁力仪经过标定后的车载磁航行实验。图中的航向角参考曲线由车载INS/GPS 组合导航系统提供。从图中可以看出:当车辆在水平行驶时，两种标定方法标定磁力仪并解算的航向角曲线都能够接近航向参考曲线;当车辆在转弯爬坡时，椭圆拟合法航向角误差远比TTLS 标定法航向角误差大。这是因为椭圆拟合法仅对水平面的二维磁力仪进行了标定，并没有考虑天向轴传感器的测量误差。由于车辆在转弯爬坡时导致天向轴磁力仪在水平投影中所占的比例增大，使得椭圆拟合法航向角解算误差增大。TTLS 标定法考虑了磁力仪天向轴分量数据的影响，并有效地抑制了病态性问题，从而提高了磁航向估计精度。

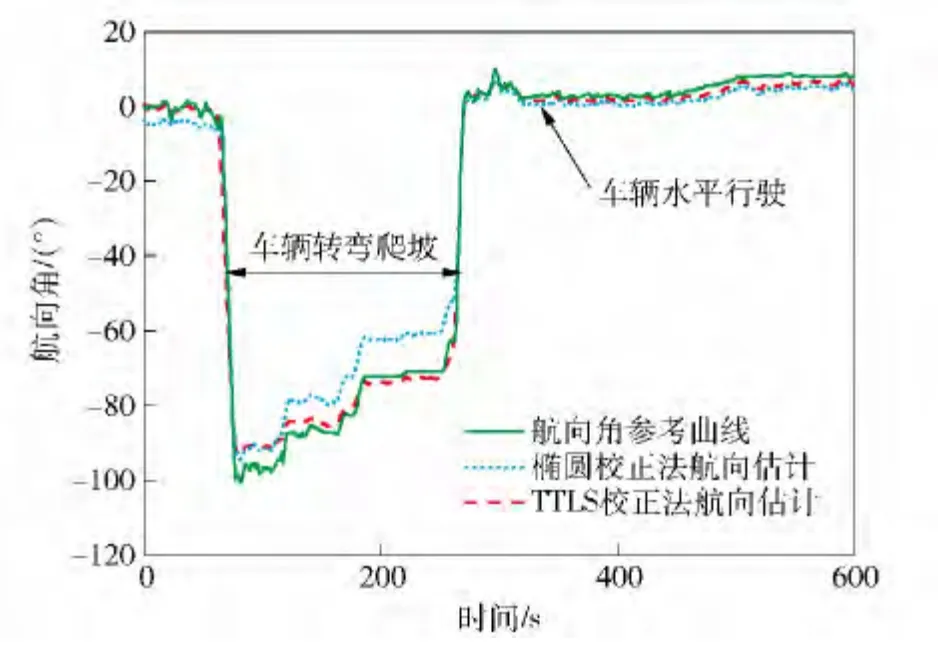
图2 椭圆拟合与TTLS 标定法航向角估计对比Fig.2 Comparison of heading estimates for TTLS and ellipse-fit algorithms

图3是两种校正算法的航向误差曲线对比。其中，实线为TTLS 校正法航向误差曲线，其平均航向角误差约为1.5°，可满足车载磁导航的精度需求［1，5-6，8］。虚线为椭圆校正法航向误差曲线，其平均航向误差约为4.5°. 通过对比可看出TTLS 校正法的优越性。

6 结论

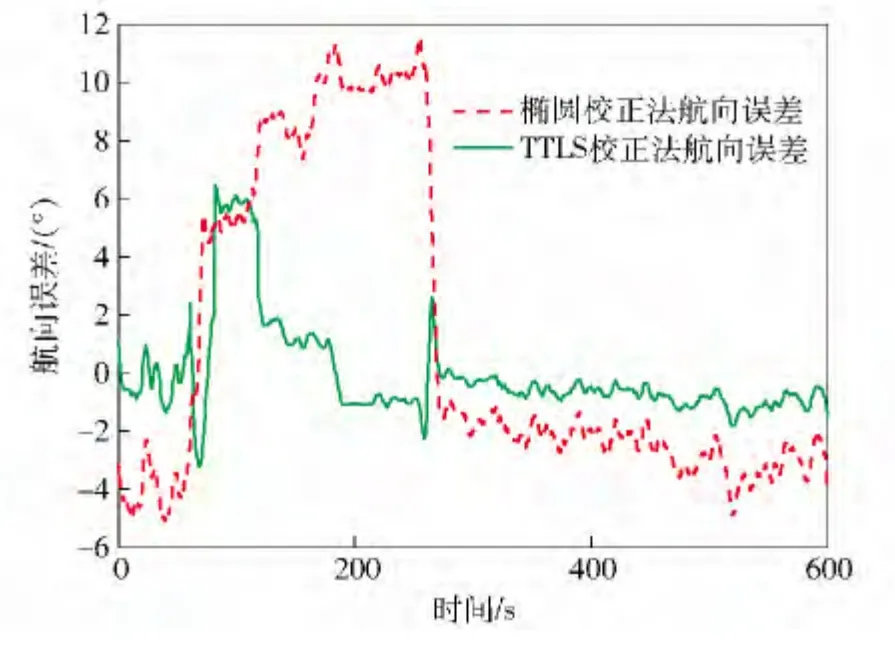
图3 航向误差曲线对比Fig.3 Comparison of heading error curves

磁力仪的标定是影响车载磁导航精度的关键技术。由于车辆机动能力受限，三轴磁力仪标定问题中的观测方程将严重病态，早先提出的三轴磁力仪标定方法如TLS 标定法有可能不再适用，因此正则化技术是必不可少的。本文提出TTLS 技术解决病态情况下的磁力仪标定问题，能够有效地抑制病态问题带来的影响，获得准确的参数估计。车载磁导航实验结果表明该方法提高了航向角估计精度和鲁棒性。

References)

［1］Caruso M J. Applications of magnetic sensors for low cost compass systems［C］∥IEEE 2000 Position Location and Navigation Symposium. San Diego，CA:IEEE，2000:177 -184.

［2］Siddharth S，Ali A S，El-Sheimy N，et al. A game-theoretic approach for calibration of low-cost magnetometers under noise uncertainty［J］. Measurement Science and Technology，2012，23(2):025003.

［3］Fang J C，Sun H W，Cao J J，et al. A novel calibration method of magnetic compass based on ellipsoid fitting［J］. IEEE Transactions on Instrumentation and Measurement，2011，60(6):2053 -2061.

［4］Foster C C，Elkaim G H. Extension of a non-linear，two-step calibration methodology to include non-orthogonal sensor axes［J］.IEEE Transactions on Aerospace Electronic Systems，2008，44(3):1070 -1087.

［5］Gebre-Egziabher D，Elkaim G H，Powell J D，et al. A non-linear，two-step estimation algorithm for calibrating solid-state strap down magnetometers［C］∥8th International Conference on Navigation Systems. St. Petersburg，Russia:IEEE/AIAA，2001:290 -297.

［6］徐玉，任沁源，孙文达，等. 微小型无人直升机地磁导航算法研究［J］. 兵工学报，2011，32(3):337 -342.XU Yu，REN Qin-yuan，SUN Wen-da，et al. A geomagnetic navigation algorithm for miniature unmanned helicopter［J］. Acta Armamentarii，2011，32(3):337 -342. (in Chinese)

［7］黄学功，王炅. 地磁信号检测系统误差分析与补偿方法研究［J］. 兵工学报，2011，32(1):33 -36.HUANG Xue-gong，WANG Jiong. Error analysis and compensation methods for geomagnetic signal detection system［J］. Acta Armamentarii，2011，32(1):33 -36. (in Chinese)

［8］Renaudin V，Afzal M H，Lachapelle G. Complete triaxis magnetometer calibration in the magnetic domain［J］. Journal of Sensors，2010，2010:1 -9.

［9］吴志添，武元新，胡小平，等. 基于总体最小二乘的捷联三轴磁力仪标定与地磁场测量误差补偿［J］. 兵工学报，2012，33(10):1202 -1209.WU Zhi-tian，WU Yuan-xin，HU Xiao-ping，et al. Calibration of strapdown three-axis magnetometer and measurement error compensation of geomagnetic field based on total least squares［J］. Acta Armamentarii，2012，33(10):1202 -1209.(in Chinese)

［10］Honerkamp J，Weese J. Tikhonovs regularization method for illposed problems［J］. Continuum Mechanics and Thermodynamics，1990，2(1):17 -30.

［11］Fierro R D，Golub G H，Hansen P C，et al. Regularization by truncated total least squares［J］. SIAM Journal on Scientific Computing，1997，18(4):1223 -1241.

［12］Mclean S，Macmillan S. The US/UK world magnetic model for 2005—2010［R］. Nottingham，UK:British Geological Survey，2004.

［13］Bonnet S，Bassompierre C，Godin C，et al. Calibration methods for inertial and magnetic sensors［J］. Sensors and Actuators A:Physical，2009，156(2):302 -311.

［14］Wu Z T，Wu Y X，Hu X P，et al. Calibration of three-axis strapdown magnetometers using particle swarm optimiazation algorithm［C］∥IEEE International Symposium on Robotic and Sensors Environments. Montreal，Canada:IEEE，2011:160 -165.

［15］Golub G H，Van Loan C F. An analysis of the total least squares problem［J］. SIAM Journal on Numerical Analysis，1980，17(6):883 -893.

［16］Markovsky I，Van Huffel S. Overview of total least-squares methods［J］. Signal Processing，2007，87(10):2283 -2302.

［17］Sima D M，Van Huffel S. Level choice in truncated total least squares［J］. Computational Statistics ＆ Data Analysis，2007，52(2):1103 -1118.

［18］Hansen P C，O'Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems［J］. SIAM Journal on Scientific Computing，1993，14(6):1487 -1803.

［19］陈希孺，王松桂. 近代回归分析［M］. 合肥:安徽教育出版社，1987.CHEN Xi-ru，WANG Song-gui. Advanced in regression analysis［M］. Hefei:Anhui Education Press，1987. (in Chinese)

［20］张晓明，赵剡. 基于椭圆约束的新型载体磁场标定及补偿技术［J］. 仪器仪表学报，2009，30(11):2438 -2443.ZHANG Xiao-ming，ZHAO Yan. New auto-calibration and compensation method for vehicle magnetic field based on ellipse restriction［J］. Chinese Journal of Scientific Instrument，2009，30(11):2438 -2443. (in Chinese)