某型转管航炮对空中目标射击命中概率分析
2015-02-22齐晓林左金雨孟新强王征
齐晓林,左金雨,2,孟新强,王征
(1.空军工程大学航空航天工程学院,西安710038;2.解放军95703部队,云南陆良655600;3.空军装备研究院,北京100076)
某型转管航炮对空中目标射击命中概率分析
齐晓林1,左金雨1,2,孟新强1,王征3
(1.空军工程大学航空航天工程学院,西安710038;2.解放军95703部队,云南陆良655600;3.空军装备研究院,北京100076)
研究了影响航炮射击的误差因素,对误差的构成及其分布特性进行了分析。研究目标在命中平面上的投影面积,得出目标投影面积的计算方法,并进行了等效简化。在此基础上,计算航炮对空中目标射击的单发命中概率和连发数为k时的命中概率。利用MATLAB编写程序求解航炮射击命中概率,以某型六管航炮为例对其在不同射速条件下对目标的命中概率进行了数值计算,为航炮的作战使用提供参考。
航炮,命中概率,误差,投影面积,数值计算
0 引言
作战飞机性能的提高,对航炮武器的性能提出了更高要求。特别是作战飞机速度和机动性的提高,使得可供航炮一次射击的时间越来越短。从发展趋势看,航炮射击的时间将减少到1 s以内[1]。因此,要求航炮有较高的射速,以便在短时间内能发射更多的弹丸,满足击毁(伤)空中高速高机动性目标必须的命中发数和毁伤概率。
1 射击误差
航炮射击时,由于跟踪系统测量目标时参数存在误差,火控系统在解算运动参数、求解弹道方程、计算射击诸元及瞄准时也存在误差,各种气象弹道条件的偏差量也存在误差,火力系统射击存在散布误差。因此,使得弹道不一定同目标相遇,即弹道对目标产生误差。为了描述这种误差,建立如下的坐标系:以目标中心为原点,过目标做一个同斜距离D垂直的平面Q作为坐标平面。在平面Q上做直角坐标系Mx1x2。x1轴是平面Q同过斜距离的垂直面即射面的交线,正向朝上。x2轴与x1轴垂直,正向与航路正向同侧。当x2轴与航路垂直时,正向可任意取定,如下页图1所示[2]。
射击过程中目标在航路上运动,该坐标系也随之运动。射击时弹道在平面Q上的坐标X描述了弹道对目标的误差,称为射击误差。它是二维正态变量:

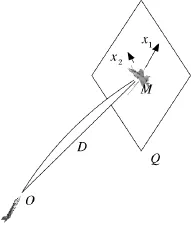
图1 射击弹道与目标相对位置示意图
分量x1称为高低误差,分量x2称为方向误差。
射击误差X的期望a称为系统误差:
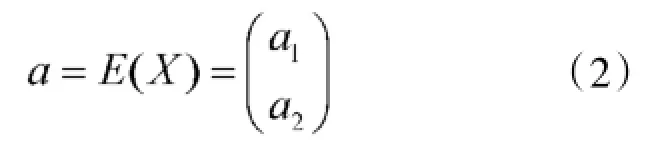
分量a1称为高低系统误差,分量a2称为方向系统误差。
射击误差X的协方差阵记为∑:
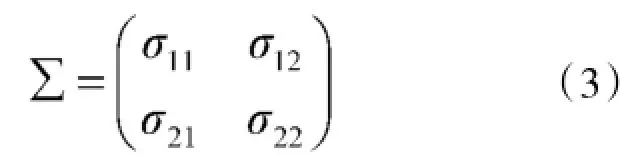
其中,σij是误差xi与xj的协方差,即:
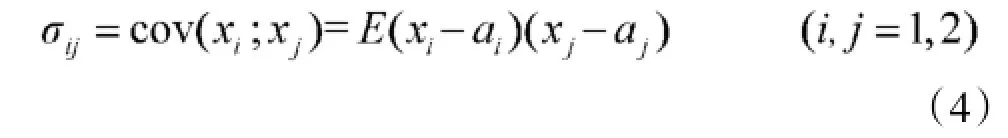
上述射击误差是在某时刻t上表述的。考虑到时间t的变化,射击误差便表示为X(t),它是一个二维的正态过程。它的期望a(t)=EX(t)是时刻t的函数。协方差阵∑(t)=σij(t)中的元素σij(t)也是时刻t的函数。a(t)与∑(t)描述了在时刻t上误差X(t)的统计特性[3]。
按误差随时间变化的相关性进行分类,有:

其中,Xb(t),Xr(t),Xg(t)为独立的误差。
射击误差X的协方差阵∑同上述3种误差的协方差阵的关系为:
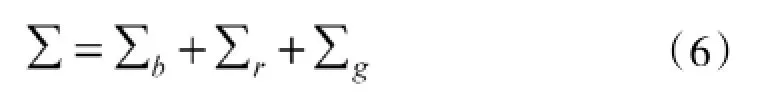
在射击误差X的3种误差Xb,Xr,Xg中,不相关误差Xb与强相关误差Xg的期望为零,只有弱相关误差的期望不为零,而等于ar。由此,射击误差X的期望a=ar。
在任一时刻上,射击误差X的分布为:

2 射击命中概率分析
航炮在射击时,由于双方均处于高速运动状态,所以对目标的命中能力较低。分析航炮射击的单发命中概率,只是出于理论研究的需要。在作战中,为了提高航炮对空中目标的命中概率,通常采用连射,也就是所谓的点射。命中概率的含义即为航炮进行一次点射,至少有一发或一发以上弹丸命中目标的概率。点射的时间称为点射长度。
2.1目标投影面积
在计算命中目标的概率时,需要知道目标在坐标平面Q上的投影面积。
把目标机作为一个长方体,它的3个截面面积分别记为[4]:
水平截面面积Sxy;纵向截面面积Syz;横向截面面积Szx。
这3个截面面积所在平面是相互垂直的,如图2所示。

图2 飞机三向视图
设空间有平面P与Q,这两平面的法矢记为nP与nQ。给出一个已知矢量T。在平面P上有面积为SP的区域,此区域沿矢量T在平面Q上投影得出另一区域,区域的面积为SQ。可以推出这两个面积的关系为:

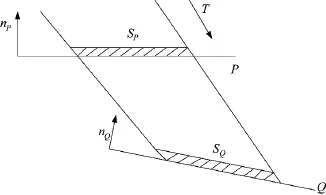
图3 投影面积图
研究在命中点MT处,目标沿弹道切线T在坐标平面Q上的投影面积。设目标航路倾角为λ,航路角为q*。
目标三向面积的各个面积沿弹道在平面Q上的投影面积为:
水平面积Sxy的投影面积Sxy*:

得出目标在平面Q的投影面积后,将目标域作为一个方形域,边长为2l。边长之半l应等于:

目标域为:

2.2射击发数为k时的命中概率
设航炮进行了一次点射,射速为u(发/分),射弹数为k。点射中相邻两次发射的时间间隔为Δ,点射的时间长度=(k-1)Δ。
由于点射时间长度不大,因此,射击误差在任一发射时刻上的统计特征可以近似为相同。即在点射的时间区间中,系统误差为常列阵,各协方差阵∑b,∑r,∑g为常方阵。它们的数据按点射时间区间的中点时刻相应的命中点位置来计算。这个中点时刻记为t0,点射的时间区间为(t0-/2,t0+/2)。时刻t0相应的命中点为MT。在t∈(t0-/2,t0+/2)的误差Xb(t),X(rt),X(gt)的协方差阵∑b,∑r,∑g及系统误差a,都在命中点MT处加以计算[5]。
射击误差X(t)的模型为三类误差模型:
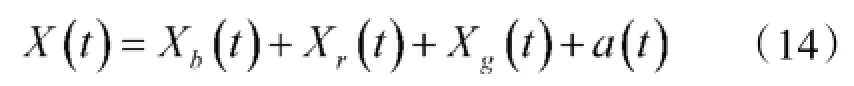
为了计算点射命中概率,需要将三类误差模型转为两类误差模型:
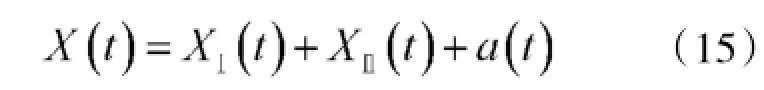
将三类误差模型转为两类误差模型的实质,就是将弱相关误差Xr分解为两个独立部分:

Xrb的协方差阵记为∑rb,Xrg的协方差阵记为∑rg:

其中,∑r为弱相关误差的协方差阵。
将弱相关误差分解后,第一类误差即独立误差为:

第二类误差(重复误差)为:

这两类误差对应的协方差阵分别为:
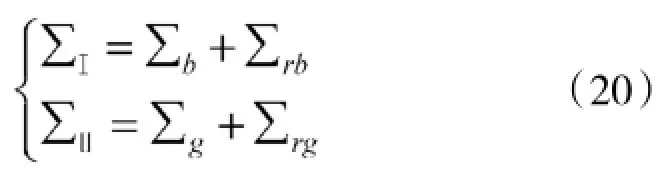
将射击误差转为两类误差模型后,则可建立一次点射的命中概率pk的公式:
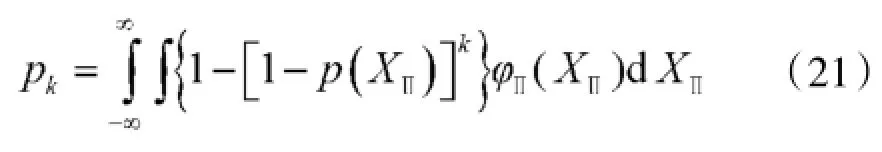
式中,p(XⅡ)是重复误差为XⅡ的条件下,一次发射命中目标的条件概率。
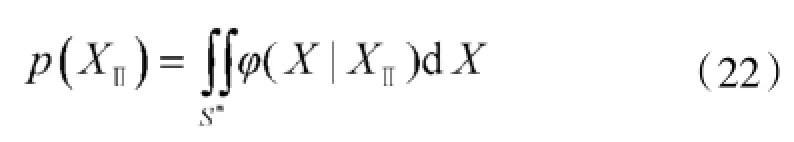
式中,φ(X|XⅡ)是重复误差为XⅡ的条件下,射击误差X的条件分布。

φⅠ(XⅠ)为独立误差XⅠ的分布密度。
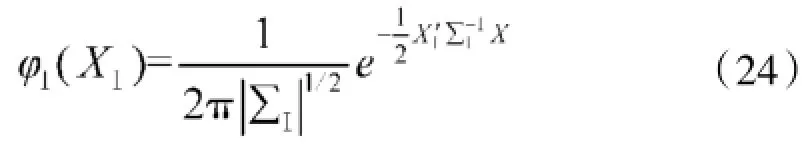
于是命中条件概率p(XⅡ)也可写为:
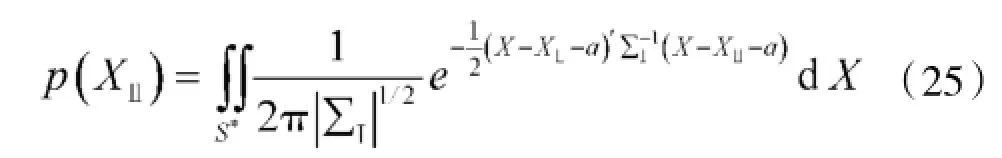
φⅡ(XⅡ)为重复误差的分布密度:
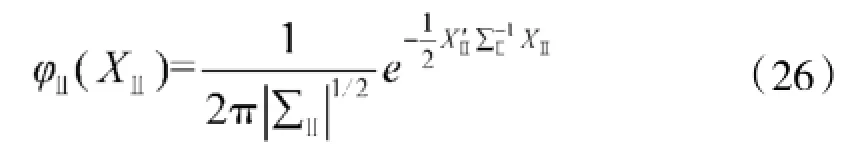
2.3命中概率数值求解
利用MATLAB编写程序求解航炮射击命中概率,程序流程如下页图4所示。
3 仿真计算
条件设定:以空战中典型的盘旋机动攻击为例。
1)目标作盘旋机动,VM=1.5 Ma;
2)跟踪射击,一次连射为0.7 s;
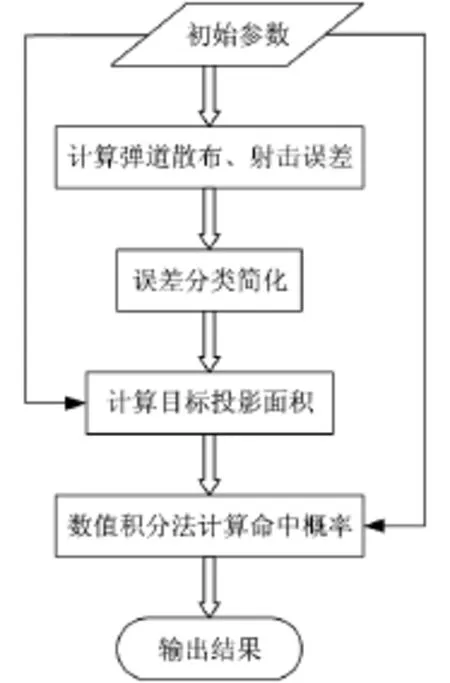
图4 命中概率数值求解流程图
3)某目标机三向面积分别为:水平截面面积Sxy=110 m2,纵向截面面积Syz=33 m2;横向截面面积Szx=8 m2。
攻击机速度大于目标,模拟某型航炮在不同距离上对作盘旋机动的目标进行射击,通过仿真计算,射击效果如表1所示。
由仿真计算结果可以看出:
对盘旋机动目标射击,当某型航炮以4000发/分射速,在600 m~1 000 m距离上对目标进行射击,以5 000发/分射速和6 000发/分射速,在600 m~1 200 m距离上对目标进行射击,可确保有一发以上的弹丸命中目标;某型航炮以5000发/分射速在600 m距离上对目标进行射击,以6 000发/分射速,在600 m~800 m距离上对目标进行射击,可确保有二发以上的弹丸命中目标。
4 结束语
航炮攻击作为作战训练的科目之一,是战法演练的重要一环。因此,研究航炮作战使用,评估其作战效能,是战法研究和工程技术人员需要关注的问题。评价航炮是否达到各项设计指标并满足战术要求,最终需要装机进行实弹射击检验。显然,空中实弹射击的成本较高,牵扯的因素多,困难较大。近年来,随着计算机技术的发展,根据射击条件建立外弹道模型,通过仿真计算得出典型条件下航炮对目标的命中概率,评定航炮是否满足作战需要,已经成为评定航炮武器作战效能的有力手段之一。

表1 某型航炮对盘旋机动目标射击效果,V1>VM
[1]齐晓林.航空自动武器[M].北京:国防工业出版社,2008:1-2.
[2]孟新强.典型条件下某型航炮作战使用研究[D].西安:空军工程大学,2012.
[3]李宁,齐晓林,李望西.基于战例仿真的航炮射击评估系统及应用[J].火炮发射与控制学报,2011(3):40-41.
[4]潘承泮.武器系统射击效力[M].北京:兵器工业出版社,1994:167-187.
[5]张培忠,米中贺,陈国利.某型转管炮立靶密集度试验条件相容性研究[J].火炮发射与控制学报,2012(3):1-4.
Hit Probability Analysis of Aircraft Gun Shooting
QI Xiao-lin1,ZUO Jin-yu1,2,MENG Xin-qiang1,WANG Zheng3
(1.Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China;
2.Unit 95703 of PLA,Luliang 655600,China;3.Air Force Academy of Armament,Beijing 100076,China)
The components and distribution characteristics of the error factors influenced the gun firing are studied.Through calculating the projected area of the target on the hit section,the single shot probability and the volley probability of gun firing is concluded.Using MATLAB to calculate the hit probability of gun firing,the calculation process of hit probability is given.Taking the 6 barrels Gatling aircraft gun as an example,the hit probability in different rapidity of fire is calculated,which can give advices for its usage of army.
aircraft gun,hit probability,error factors,projected area,calculating
TJ392
:A
1002-0640(2015)01-0080-04
2013-11-25
2014-01-07
齐晓林(1965-),男,陕西泾阳人,硕士,副教授。研究方向:航空武器控制理论与技术。
